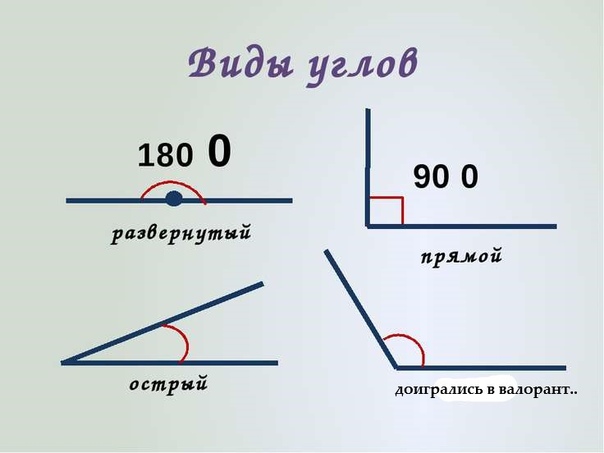
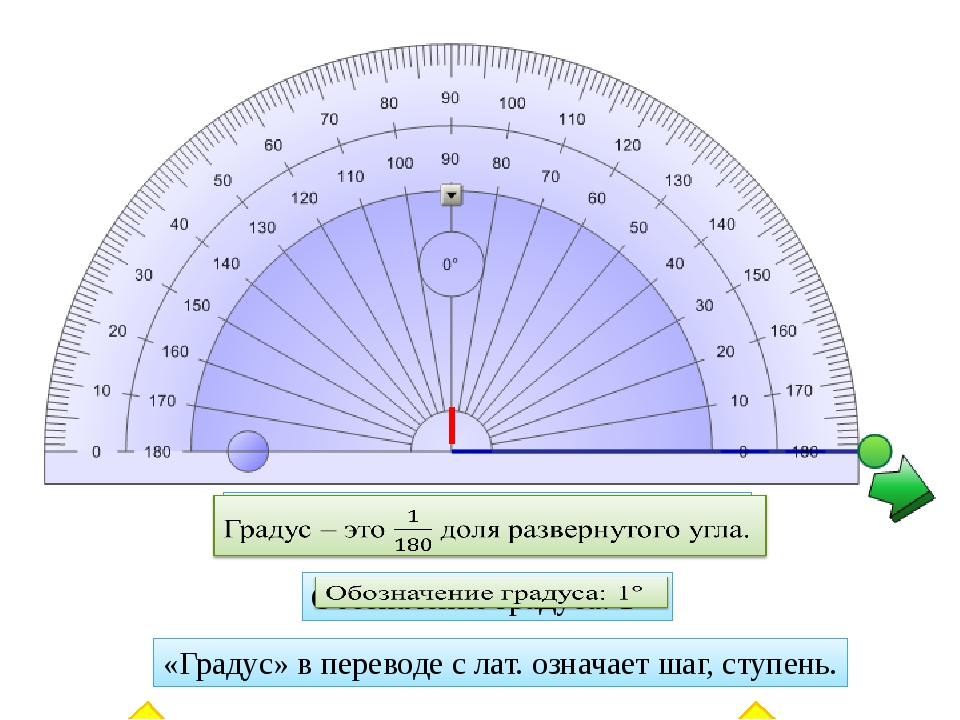
Угол в 30 градусов, угол в 60 градусов— как получить?
При наличии транспортира отмерить любые углы можно, как говориться в два счета, а при его отсутствии задача становиться потруднее.
Сбегав в магазин и купив транспортир получить угол 30 градусов, угол 60 градусов, как впрочем и любой другой можно за несколько секунд.
Но, нам нужно получить нужный угол прямо сейчас, не бегая по магазинам, и не совершая ненужных покупок. Возможно ли это? Да с легкостью!
Берем обыкновенный квадратный лист бумаги и сворачиваем как на рисунке.
В итоге у нас получился тот же самый квадрат, но разделенный по середине линией. Только нужные нам углы мы еще не поучили.
Это поправимо, идем дальше.
Что у нас получилось в итоге? На листе получилась дополнительная линия, она пересекает наш квадрат на две равные части.
Теперь очередь за разметкой квадрата.
Назовем одну сторону, из которой отходит полученная линия, буквами АВ.
А точку пересечения дополнительной линии со стороной АВ обозначим точкой С.
Теперь начинаем строить треугольник. Измерим расстояние АВ, и отложим отрезок такой же длины из точки А до пересечения с дополнительной линией. Получим точку D.
Замерим расстояние DВ, оно должно равняться отрезку AD. Если вдруг равенства не получилось, то проверьте все ли сделано правильно.
Не допущены ли слишком большие погрешности?
Если после тщательной проверки, расстояния все же не совпадают, это может означать только одно. Вы открыли совершенно не знакомый науке вид геометрии, и Вам светит, как минимум, Нобелевская премия.
Но все же остановимся на варианте когда у нас расхождений нет.
Что мы имеем в итоге? Получился треугольник АВD у которого все стороны равны, а как известно у равностороннего треугольника еще и все углы тоже равны и имеют одинаковое значение в 60 градусов.
Итог — угол 60 градусов получен, это любой из углов нашего треугольника.
А где теперь взять угол в 30 градусов? Да там же! Угол D разделен линией СD наполовину.
Поэтому угол 30 градусов это любой из углов АDС или ВDС на выбор.
Еще по теме:
Измерение угла косоглазия — клиника Семейный доктор
Измерение угла косоглазия осуществляется в градусах. От того, насколько точно была проведена диагностика, зависит выбор направления дальнейшего лечения. Так, при значении угла более 15 градусов, с целью повышения остроты зрения, врач может порекомендовать хирургическое вмешательство. При меньшем параметре врач предложит индивидуальное лечение, включая аппаратную коррекцию нарушения зрения.
Методы измерения
Наиболее известным считается метод Гиршберга. Для этого используется офтальмоскоп, который располагается перед пациентом. Обследуемый смотрит прямо на отверстие аппарата, а врач обращает внимание на расположение световых бликов на глазах. На глазу, расположенном ровно, блик фиксируется посередине зрачка. Блик на косящем глазу смещается от центра. Если это происходит в пределах зрачка, речь идет о значении менее 15 градусов, а при расположении на радужке – 25-30 градусов.
Если это происходит в пределах зрачка, речь идет о значении менее 15 градусов, а при расположении на радужке – 25-30 градусов.
Измерение угла косоглазия с помощью периметра подразумевает проведение исследования в темной комнате. Пациент устанавливает подбородок на подставку и фиксирует взгляд на свече, закрепленной на душе рамочного периметра. Специалист оценивает, на какой отметке дуги зафиксировать вторую свечу, чтобы она отражалась в другом зрачке.
Применение синоптофора подразумевает участие пациента: он перемещает ручки, чтобы совместить две картинки в единое изображение. Картинки в свою очередь установлены в кассеты. Попеременное выключение подсвечивания объектов нужно, чтобы остановить установочные движения глазных яблок. Оно выполняется вручную или в автоматическом режиме. Параметры определяются по специальной шкале. Стоит отметить, что во время работы аппарата пациент тренирует глазную мускулатуру, поэтому процедура может иметь не только диагностическое, но и терапевтическое значение. Синоптофор позволяет корректировать косоглазие, как у маленьких, так и у взрослых пациентов.
Синоптофор позволяет корректировать косоглазие, как у маленьких, так и у взрослых пациентов.
Важно понимать, что измерение угла косоглазия не единственное обследование, которое проводится при такой патологии глаз. По назначению врача важно также пройти комплексное обследование: визометрию, исследование объема движения глаз, оценку характера зрения, изучение состояния сетчатки, зрительного нерва и пр. На основании полученных результатов врач даст рекомендации по поводу корректирующих мероприятий, направленных на улучшение зрения.
Пройти комплексное обследование глаз вы можете, обратившись в клинику «Семейный доктор». Современное оснащение диагностической аппаратурой позволяет точно определить параметры угла косоглазия, оценить общее состояние зрительной системы и правильно выбрать направление коррекции или лечения.
Для записи на удобное для Вас время, позвоните по телефону единого контакт-центра в Москве +7 (495) 775 75 66, заполните форму on-line записи или обратитесь в регистратуру клиники. \circ$.
\circ$.
math-public/pryamougolnyj-treugolnik-s-uglom-v-30-gradusov.txt · Последнее изменение: 2019/09/03 23:13 — labreslav
| Фигура | Рисунок | Формулировка |
| Прямоугольный треугольник | Треугольник, у которого один из углов равен 90°, называют прямоугольным треугольником. Сторону, лежащую против угла в 90°, называют гипотенузой, две другие стороны называют катетами. | |
Катеты прямоугольного треугольника | Длины катетов прямоугольного треугольника меньше длины гипотенузы. | |
| Равнобедренный прямоугольный треугольник | Равнобедренным прямоугольным треугольником называют такой прямоугольный треугольник, у которого равны катеты. | |
| Прямоугольный треугольник с углом в 30° | Катет прямоугольного треугольника, лежащий против угла в 30°, равен половине гипотенузы. | |
Катет, равный половине гипотенузы | Если в прямоугольном треугольнике один из катетов равен половине гипотенузы, то этот катет лежит против угла в 30°. | |
Медиана, проведённая к гипотенузе прямоугольного треугольника | Медиана прямоугольного треугольника, проведённая из вершины прямого угла, равна половине гипотенузы. Посмотреть доказательство | |
Медиана треугольника, равная половине стороны, к которой она проведена | Если в треугольнике медиана равна половине стороны, к которой она проведена, то такой треугольник является прямоугольным. | |
Центр описанной окружности | Середина гипотенузы прямоугольного треугольника является центром описанной около него окружности. Посмотреть доказательство | |
Если в треугольнике центр описанной окружности лежит на одной из сторон, то этот треугольник является прямоугольным треугольником, а центр описанной окружности совпадает с серединой гипотенузы. | ||
Теорема Пифагора | В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов c2 = a2 + b2 Посмотреть доказательство | |
Обратная теорема Пифагора | Если в треугольнике квадрат одной стороны равен сумме квадратов двух других сторон, то такой треугольник является прямоугольным |
Таблица СИНУСОВ для углов от 0° до 360° градусов
СИНУС (SIN α) — это одна из прямых тригонометрических функций для углов, в прямоугольном треугольнике синус острого угла равен отношению противолежащего катета к его единственной гипотенузе.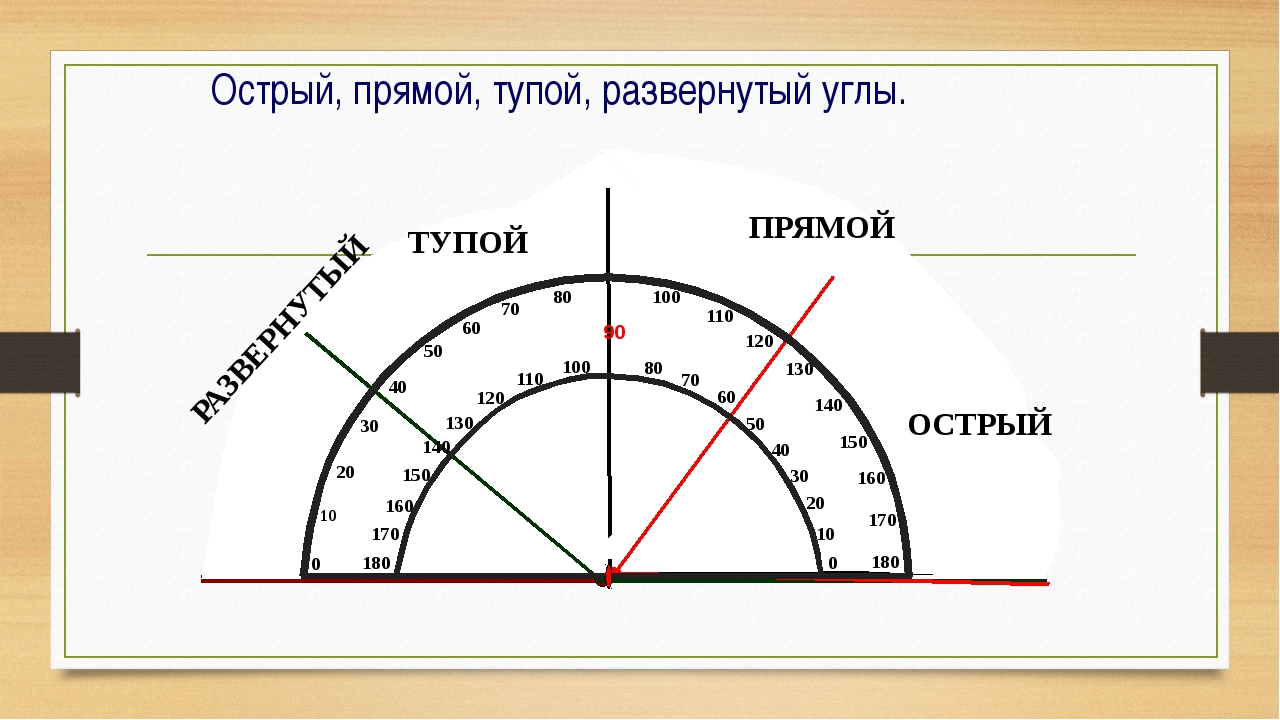
| α (радианы) | 0 | π/6 | π/4 | π/3 | π/2 | π | √3π/2 | 2π |
|---|---|---|---|---|---|---|---|---|
| α (градусы) | 0° | 30° | 45° | 60° | 90° | 180° | 270° | 360° |
| SIN α (СИНУС) | 0 | 1/2 | √2/2 | √3/2 | 1 | 0 | -1 | 0 |
…
| Угол в градусах | Sin (Синус) |
|---|---|
| 0° | 0 |
| 1° | 0.0175 |
| 2° | 0.0349 |
| 3° | 0.0523 |
| 4° | 0.0698 |
| 5° | 0.0872 |
| 6° | 0.1045 |
| 7° | 0.1219 |
| 8° | 0.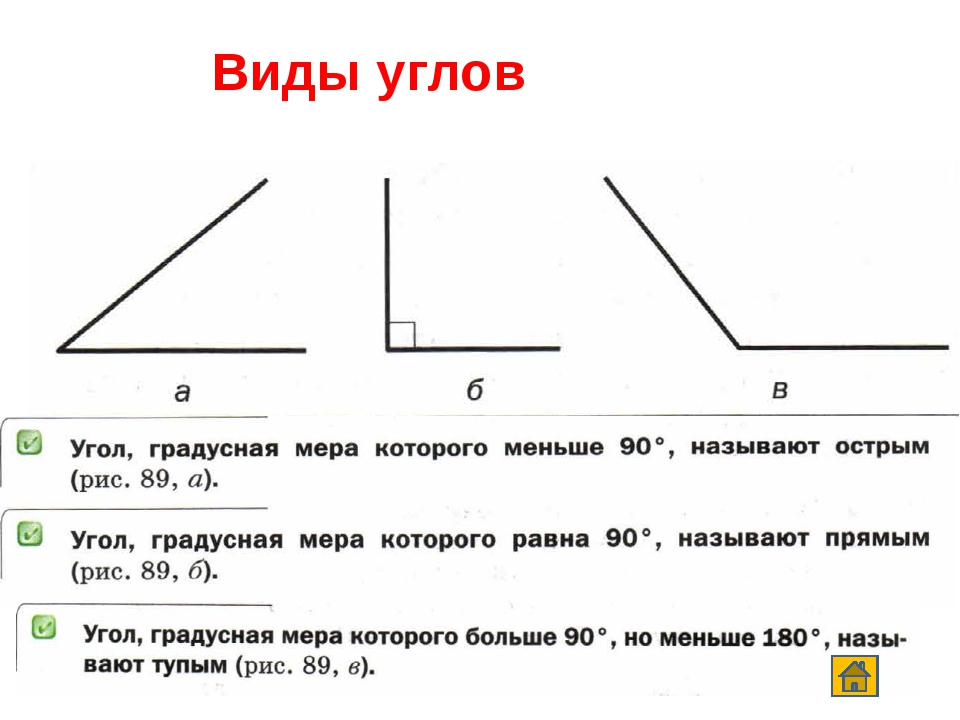 1392 1392 |
| 9° | 0.1564 |
| 10° | 0.1736 |
| 11° | 0.1908 |
| 12° | 0.2079 |
| 13° | 0.225 |
| 14° | 0.2419 |
| 15° | 0.2588 |
| 16° | 0.2756 |
| 17° | 0.2924 |
| 18° | 0.309 |
| 19° | 0.3256 |
| 20° | 0.342 |
| 21° | 0.3584 |
| 22° | 0.3746 |
| 23° | 0.3907 |
| 24° | 0.4067 |
| 25° | 0.4226 |
| 26° | 0.4384 |
| 27° | 0.454 |
| 28° | 0.4695 |
| 29° | 0.4848 |
| 30° | 0.5 |
| 31° | 0.515 |
| 32° | 0.5299 |
| 33° | 0.5446 |
| 34° | 0.5592 |
| 35° | 0. 5736 5736 |
| 36° | 0.5878 |
| 37° | 0.6018 |
| 38° | 0.6157 |
| 39° | 0.6293 |
| 40° | 0.6428 |
| 41° | 0.6561 |
| 42° | 0.6691 |
| 43° | 0.682 |
| 44° | 0.6947 |
| 45° | 0.7071 |
| 46° | 0.7193 |
| 47° | 0.7314 |
| 48° | 0.7431 |
| 49° | 0.7547 |
| 50° | 0.766 |
| 51° | 0.7771 |
| 52° | 0.788 |
| 53° | 0.7986 |
| 54° | 0.809 |
| 55° | 0.8192 |
| 56° | 0.829 |
| 57° | 0.8387 |
| 58° | 0.848 |
| 59° | 0.8572 |
| 60° | 0.866 |
| 61° | 0.8746 |
| 62° | 0.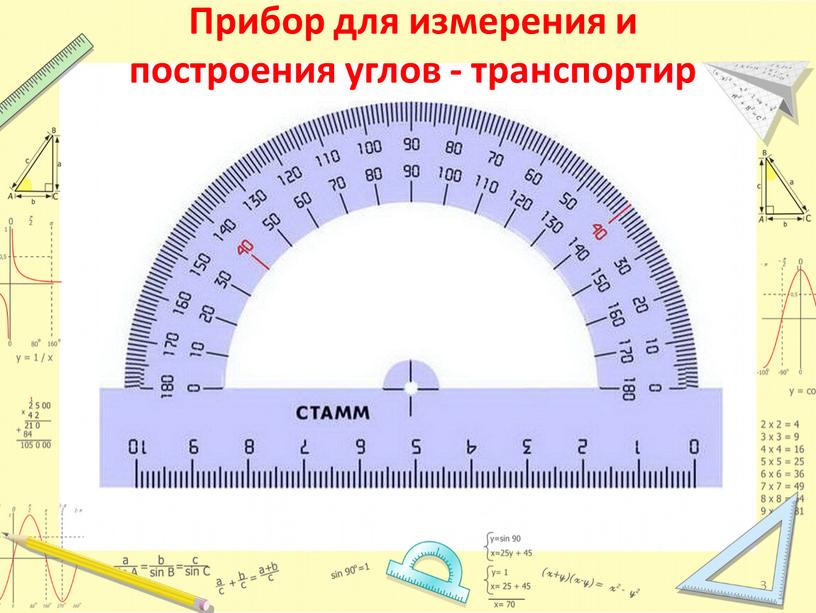 8829 8829 |
| 63° | 0.891 |
| 64° | 0.8988 |
| 65° | 0.9063 |
| 66° | 0.9135 |
| 67° | 0.9205 |
| 68° | 0.9272 |
| 69° | 0.9336 |
| 70° | 0.9397 |
| 71° | 0.9455 |
| 72° | 0.9511 |
| 73° | 0.9563 |
| 74° | 0.9613 |
| 75° | 0.9659 |
| 76° | 0.9703 |
| 77° | 0.9744 |
| 78° | 0.9781 |
| 79° | 0.9816 |
| 80° | 0.9848 |
| 81° | 0.9877 |
| 82° | 0.9903 |
| 83° | 0.9925 |
| 84° | 0.9945 |
| 85° | 0.9962 |
| 86° | 0.9976 |
| 87° | 0.9986 |
| 88° | 0.9994 |
| 89° | 0. 9998 9998 |
| 90° | 1 |
…
| Угол в градусах | Sin (Синус) |
|---|---|
| 91° | 0.9998 |
| 92° | 0.9994 |
| 93° | 0.9986 |
| 94° | 0.9976 |
| 95° | 0.9962 |
| 96° | 0.9945 |
| 97° | 0.9925 |
| 98° | 0.9903 |
| 99° | 0.9877 |
| 100° | 0.9848 |
| 101° | 0.9816 |
| 102° | 0.9781 |
| 103° | 0.9744 |
| 104° | 0.9703 |
| 105° | 0.9659 |
| 106° | 0.9613 |
| 107° | 0.9563 |
| 108° | 0.9511 |
| 109° | 0.9455 |
| 110° | 0.9397 |
| 111° | 0.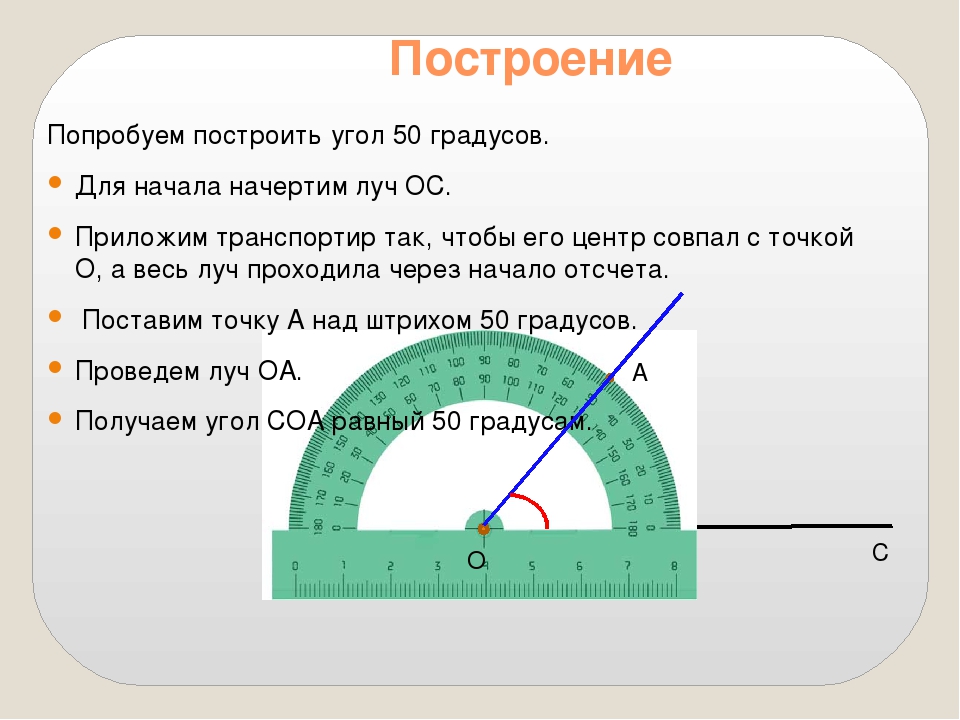 9336 9336 |
| 112° | 0.9272 |
| 113° | 0.9205 |
| 114° | 0.9135 |
| 115° | 0.9063 |
| 116° | 0.8988 |
| 117° | 0.891 |
| 118° | 0.8829 |
| 119° | 0.8746 |
| 120° | 0.866 |
| 121° | 0.8572 |
| 122° | 0.848 |
| 123° | 0.8387 |
| 124° | 0.829 |
| 125° | 0.8192 |
| 126° | 0.809 |
| 127° | 0.7986 |
| 128° | 0.788 |
| 129° | 0.7771 |
| 130° | 0.766 |
| 131° | 0.7547 |
| 132° | 0.7431 |
| 133° | 0.7314 |
| 134° | 0.7193 |
| 135° | 0.7071 |
| 136° | 0.6947 |
| 137° | 0. 682 682 |
| 138° | 0.6691 |
| 139° | 0.6561 |
| 140° | 0.6428 |
| 141° | 0.6293 |
| 142° | 0.6157 |
| 143° | 0.6018 |
| 144° | 0.5878 |
| 145° | 0.5736 |
| 146° | 0.5592 |
| 147° | 0.5446 |
| 148° | 0.5299 |
| 149° | 0.515 |
| 150° | 0.5 |
| 151° | 0.4848 |
| 152° | 0.4695 |
| 153° | 0.454 |
| 154° | 0.4384 |
| 155° | 0.4226 |
| 156° | 0.4067 |
| 157° | 0.3907 |
| 158° | 0.3746 |
| 159° | 0.3584 |
| 160° | 0.342 |
| 161° | 0.3256 |
| 162° | 0.309 |
| 163° | 0. 2924 2924 |
| 164° | 0.2756 |
| 165° | 0.2588 |
| 166° | 0.2419 |
| 167° | 0.225 |
| 168° | 0.2079 |
| 169° | 0.1908 |
| 170° | 0.1736 |
| 171° | 0.1564 |
| 172° | 0.1392 |
| 173° | 0.1219 |
| 174° | 0.1045 |
| 175° | 0.0872 |
| 176° | 0.0698 |
| 177° | 0.0523 |
| 178° | 0.0349 |
| 179° | 0.0175 |
| 180° | 0 |
…
| Угол | Sin (Синус) |
|---|---|
| 181° | -0.0175 |
| 182° | -0.0349 |
| 183° | -0.0523 |
| 184° | -0.0698 |
| 185° | -0.0872 |
| 186° | -0.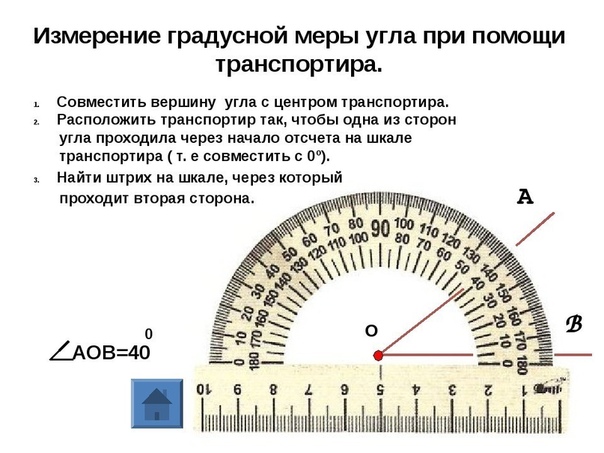 1045 1045 |
| 187° | -0.1219 |
| 188° | -0.1392 |
| 189° | -0.1564 |
| 190° | -0.1736 |
| 191° | -0.1908 |
| 192° | -0.2079 |
| 193° | -0.225 |
| 194° | -0.2419 |
| 195° | -0.2588 |
| 196° | -0.2756 |
| 197° | -0.2924 |
| 198° | -0.309 |
| 199° | -0.3256 |
| 200° | -0.342 |
| 201° | -0.3584 |
| 202° | -0.3746 |
| 203° | -0.3907 |
| 204° | -0.4067 |
| 205° | -0.4226 |
| 206° | -0.4384 |
| 207° | -0.454 |
| 208° | -0.4695 |
| 209° | -0.4848 |
| 210° | -0.5 |
| 211° | -0.515 |
| 212° | -0.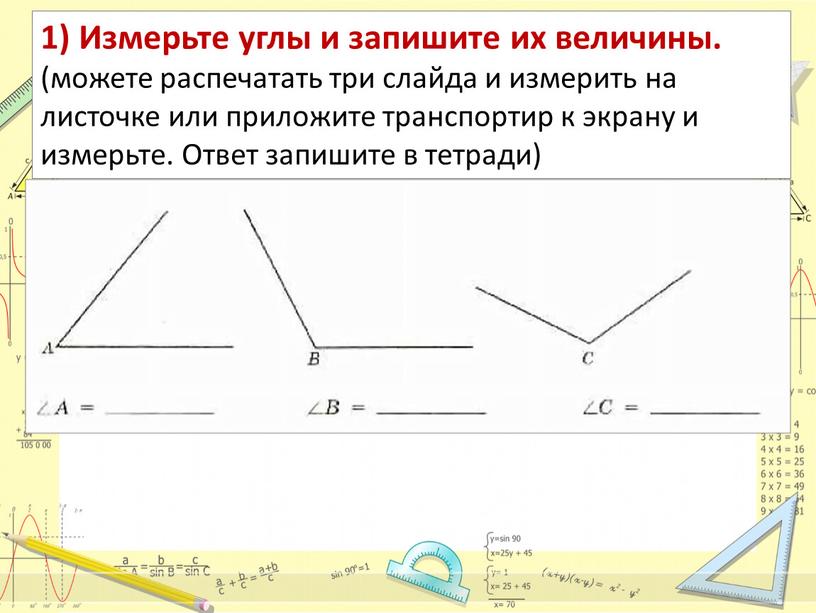 5299 5299 |
| 213° | -0.5446 |
| 214° | -0.5592 |
| 215° | -0.5736 |
| 216° | -0.5878 |
| 217° | -0.6018 |
| 218° | -0.6157 |
| 219° | -0.6293 |
| 220° | -0.6428 |
| 221° | -0.6561 |
| 222° | -0.6691 |
| 223° | -0.682 |
| 224° | -0.6947 |
| 225° | -0.7071 |
| 226° | -0.7193 |
| 227° | -0.7314 |
| 228° | -0.7431 |
| 229° | -0.7547 |
| 230° | -0.766 |
| 231° | -0.7771 |
| 232° | -0.788 |
| 233° | -0.7986 |
| 234° | -0.809 |
| 235° | -0.8192 |
| 236° | -0.829 |
| 237° | -0.8387 |
| 238° | -0.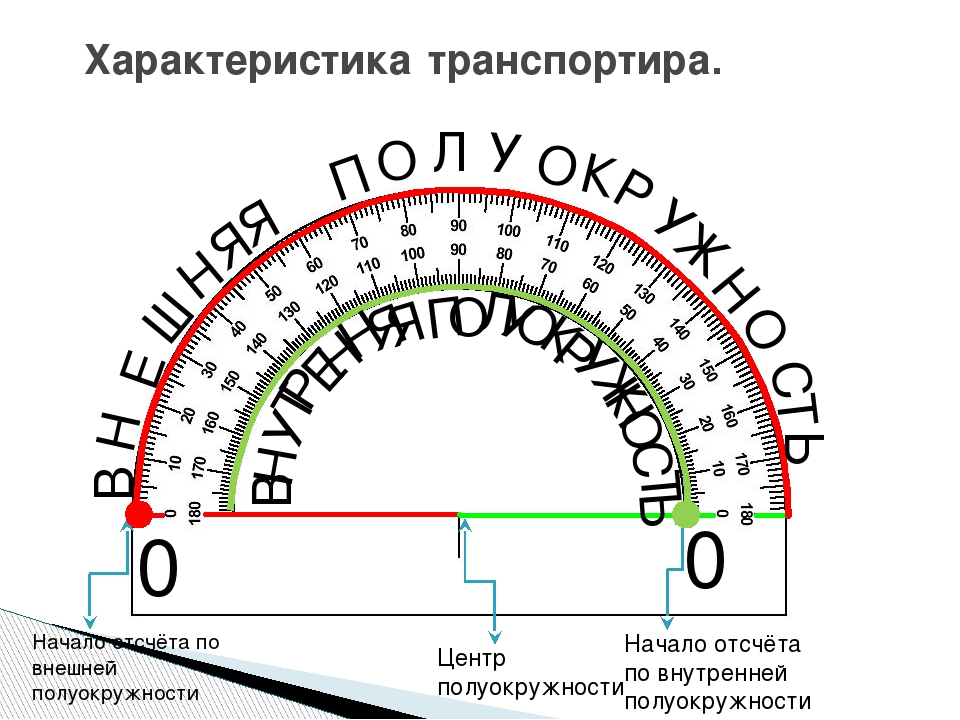 848 848 |
| 239° | -0.8572 |
| 240° | -0.866 |
| 241° | -0.8746 |
| 242° | -0.8829 |
| 243° | -0.891 |
| 244° | -0.8988 |
| 245° | -0.9063 |
| 246° | -0.9135 |
| 247° | -0.9205 |
| 248° | -0.9272 |
| 249° | -0.9336 |
| 250° | -0.9397 |
| 251° | -0.9455 |
| 252° | -0.9511 |
| 253° | -0.9563 |
| 254° | -0.9613 |
| 255° | -0.9659 |
| 256° | -0.9703 |
| 257° | -0.9744 |
| 258° | -0.9781 |
| 259° | -0.9816 |
| 260° | -0.9848 |
| 261° | -0.9877 |
| 262° | -0.9903 |
| 263° | -0.9925 |
| 264° | -0. 9945 9945 |
| 265° | -0.9962 |
| 266° | -0.9976 |
| 267° | -0.9986 |
| 268° | -0.9994 |
| 269° | -0.9998 |
| 270° | -1 |
…
| Угол | Sin (Синус) |
|---|---|
| 271° | -0.9998 |
| 272° | -0.9994 |
| 273° | -0.9986 |
| 274° | -0.9976 |
| 275° | -0.9962 |
| 276° | -0.9945 |
| 277° | -0.9925 |
| 278° | -0.9903 |
| 279° | -0.9877 |
| 280° | -0.9848 |
| 281° | -0.9816 |
| 282° | -0.9781 |
| 283° | -0.9744 |
| 284° | -0.9703 |
| 285° | -0.9659 |
| 286° | -0. 9613 9613 |
| 287° | -0.9563 |
| 288° | -0.9511 |
| 289° | -0.9455 |
| 290° | -0.9397 |
| 291° | -0.9336 |
| 292° | -0.9272 |
| 293° | -0.9205 |
| 294° | -0.9135 |
| 295° | -0.9063 |
| 296° | -0.8988 |
| 297° | -0.891 |
| 298° | -0.8829 |
| 299° | -0.8746 |
| 300° | -0.866 |
| 301° | -0.8572 |
| 302° | -0.848 |
| 303° | -0.8387 |
| 304° | -0.829 |
| 305° | -0.8192 |
| 306° | -0.809 |
| 307° | -0.7986 |
| 308° | -0.788 |
| 309° | -0.7771 |
| 310° | -0.766 |
| 311° | -0.7547 |
| 312° | -0. 7431 7431 |
| 313° | -0.7314 |
| 314° | -0.7193 |
| 315° | -0.7071 |
| 316° | -0.6947 |
| 317° | -0.682 |
| 318° | -0.6691 |
| 319° | -0.6561 |
| 320° | -0.6428 |
| 321° | -0.6293 |
| 322° | -0.6157 |
| 323° | -0.6018 |
| 324° | -0.5878 |
| 325° | -0.5736 |
| 326° | -0.5592 |
| 327° | -0.5446 |
| 328° | -0.5299 |
| 329° | -0.515 |
| 330° | -0.5 |
| 331° | -0.4848 |
| 332° | -0.4695 |
| 333° | -0.454 |
| 334° | -0.4384 |
| 335° | -0.4226 |
| 336° | -0.4067 |
| 337° | -0.3907 |
| 338° | -0. 3746 3746 |
| 339° | -0.3584 |
| 340° | -0.342 |
| 341° | -0.3256 |
| 342° | -0.309 |
| 343° | -0.2924 |
| 344° | -0.2756 |
| 345° | -0.2588 |
| 346° | -0.2419 |
| 347° | -0.225 |
| 348° | -0.2079 |
| 349° | -0.1908 |
| 350° | -0.1736 |
| 351° | -0.1564 |
| 352° | -0.1392 |
| 353° | -0.1219 |
| 354° | -0.1045 |
| 355° | -0.0872 |
| 356° | -0.0698 |
| 357° | -0.0523 |
| 358° | -0.0349 |
| 359° | -0.0175 |
| 360° | 0 |
…
Таблица синусов особенно нужна, когда у вас под рукой нет супер навороченного инженерного калькулятора с маленькой спасительной кнопкой с надписью «sin». В таком случае, чтобы узнать, чему же равняется синус определенного заданного угла, просто найдите информацию о интересующем градусе.
Как распечатать таблицу? Левой кнопкой на компьютерной мишке выделите полностью всё таблицу, на выделенном фоне нажмите уже правую кнопку мишки и в появившемся меню перейдете в пункт «Печать».
Как пользоваться таблицей? Всё гораздо проще, чем Вы думаете, ищем в левой вертикальной колонке, соответствующий градус, и напротив него и будет указано нужное значение синуса для данного нужного нам угла.
Пример
Чему равен синус 45? …
— А вот собственно и сам ответ на поставленную задачку.sin 45 = 0.7071
Автор: Bill4iam
Жизнь под углом в 30 градусов. Часть вторая, в которой все идет по плану
Продолжение. Начало здесь: Часть 1.
Четвертый день гонки, 23 марта
4 дня в море, полтора дня с настоящего старта — а ощущение, что это у нас тут расслабленный круиз и гонка еще впереди. Ветер слабый, волны нет, просыпаешься — кажется, что яхта вообще неподвижна.
Пока что самым сильным впечатлением является первая ночь после старта. Мне была поручена навигация — и все восемь часов двух ночных вахт я провела внизу, отрываясь от монитора AIS только затем, чтобы высунуться в люк и дать очередные ценные указания рулевым. Потому что происходящее вокруг описать словами довольно трудно. Но я попробую.
Возьмите лист бумаги. Нарисуйте в центре маленький кораблик. А теперь окружите этот кораблик сотней значков рыболовных сетей. Причем некоторые из этих значков отмечают сегменты одной сети (и, соответственно, проходить между ними нельзя), а некоторые — сами по себе. Теперь добавьте десяток рыболовецких судов, которые перемещаются (быстрее, чем наш маленький кораблик) и оставляют за собой все новые и новые сети. А теперь представьте, что AIS показывает нам далеко не полную картину, и если выйти на палубу, то — спасибо яркой луне — можно увидеть буйки сетей, на которых не установлен AIS.
Никогда ничего подобного раньше не видела. И больше не хочу.
Вот вам картинка, чтобы было понятнее:
— Правее! Правее бери, мы сейчас в сеть въедем! Почему мы рулим 90, нам нужно минимум 120!
— Потому что ветра нихрена нет, я вообще курс не контролирую!…
— Мы можем обогнуть этот буек справа?
— Не думаю, кажется там сеть. Держись левее, CV23 только что там прошла и они идут дальше — есть шанс, что там чисто!…
— Прекрасный, прекрасный курс! Так держать! Никуда не сворачивай, это вот прям то что надо!
— Слушайте, я ее люблю! Первый раз навигатор дает позитивную обратную связь, а не только ругается «куда ты рулишь?!»
***
Открыла дверь в машинное отделение (вот оно, кстати — да мы там сушим полотенца. И перчатки. И шапки. И даже носки. Но про это позже)
посмотрела вниз, ужаснулась. По мнению нашего механика Мартина, у нас несколько подтекает опреснитель — в любом случае, я выкачала оттуда ведра три то ли дизеля, то ли воды — теперь наше машинное отделение хоть на что-то похоже.
День шестой. Вроде бы 25 марта. Кажется, пятница
Ага, наконец-то все это стало немного похоже на гонку. Прошлой ночью было немного ажиотажа на носу (суета, сброс паруса, все мокрые, шум, крик — ну как полагается). Идем upwind, дует 35 (с порывами до 50). Ощущения от рулежки волшебные — первый раз в жизни я, наконец-то, начинаю понимать, как это делается. Самое удивительное, что я там вообще за штурвалом не нужна — ну там в особо большую волну нос направить, да изредка курс скорректировать — она сама идет, куда надо. Я так, присматриваю. Невероятное совершенно чувство — я вниз спустилась с горящими глазами, Максу рассказываю: «…кажется, моя роль как рулевого чисто номинальная — она сама знает, куда идти». Макс смеется: «Ты что, никогда не рулила яхтой с правильно выставленными парусами?»
Though I’m past
one hundred thousand miles
I’m feeling very still
And I think my spaceship knows which way to go
Удивительно тепло, кстати. С момента выхода из порта Циндао воздух становится все теплее и теплее. Вода еще теплее воздуха. Я-то думала, нам придется снег с палубы сметать да лед скалывать с такелажа… А мы раздеваемся на глазах.
День седьмой
Какой сегодня по счету день гонки я знаю из висящего на стене расписания: кто что сегодня делает. Оттуда же можно узнать о том, какой сегодня день недели (по крайней мере до того момента, как мы пересечем линию смены дат). Число и месяц интересуют только того, кто назначен сегодня на роль навигатора — кто-то полагается на свои часы, кто-то — на предыдущих навигаторов и подглядывает на вчерашнюю страницу корабельного журнала, чтобы узнать дату.
Вахтенная система у нас организована следующим образом: сутки начинаются в 7 утра, две вахты по 6 часов (с 7 утра до часу дня и с часу дня до 7 вечера), затем 3 четырехчасовые вахты. Судовой журнал ведется, ясно дело, в UTC («локальное» время, которое мы довольно условно выставляем исходя из принципа «в 7 вечера должно начинать смеркаться, а в 3 утра еще должно быть темно» тоже указывается). Есть расписание, кто что делает каждый день: кто «mother» (готовит еду), кто отвечает за уборку гальюнов, кто воду из трюмов откачивает, кто навигирует. На каждую роль выделяется 1 человек из каждой вахты, за исключением «mother» — дежурный по камбузу исключается на сутки из вахтенной системы. Его (ее) день начинается около половины шестого, чтобы в 6:30 уже кормить завтраком тех, кто заступает на вахту в 7 утра — и затем тех, кто только что закончил вахту. Затем целый день mother готовит обед-ужин-печет хлеб (да! мы печем хлеб. Каждый день. У нас есть электрический тостер и эти сибариты не представляют себе жизни без тостов на завтрак!), и после ужина отправляется спать — на всю ночь и даже больше, поскольку расписание составлено хитро и на следующий день вахта у того, кто был вчера mother, начинается аж в час дня. Т.е. если быстро управиться с мытьем посуды после ужина, то спать можно лечь часов в 9, и спать аж до полудня. Но все это означает, что mother не несет вахты и, следовательно, на палубе может не хватать рук. Нас всего 15 человек (плюс шкипер), поэтому на роль mother каждый день назначается только один человек (чтобы минимизировать потери людей на палубе), а кто-то из второй вахты назначается «mother-in-law» и спускается вниз, когда mother требуется помощь — обычно это час до и час после завтрака/обеда/ужина — помочь с раздачей еды/мытьем посуды.
В то, что существует какая-то жизнь за пределами лодки, верится с трудом — в основном, благодаря стандартным ночным разговорам на палубе: «а вот когда мы финишируем, тут-то я (варианты: выпью пива/приму душ/etc). Я со своим вариантом пока не определилась: «То ли сначала в горячую ванну, а потом устриц с шампанским, то ли сначала устриц с шампанским, а потом в горячую ванну? Или в ванну с бокалом шампанского?»
Тем временем мы прошли первую тысячу миль, впереди еще около четырех с половиной тысяч. Наконец обе наши вахты определились с названиями. Наша семерка назвала себя «Ocean’s Seven», а вот вторая вахта — под руководством польского паренька Павла — с его подачи — называется Pussy Riot. Я немедленно поинтересовалась, где и когда они будут петь и танцевать…
Занятно, что среди «Pussy Riot» — пожилая, очень серьезная и довольно религиозная женщина Сью, наводящая, несмотря на хрупкое телосложение и едва слышный голос, ужас на всех нарушителей общественного порядка на борту.
— И что сказала Сью на такое название вашей вахты?
— Мне кажется, она еще не осознала…
***
На общий корабельный email присылают блоги всех шкиперов за день. Говорят, если верить блогу, на борту «Unicef» две курицы-несушки. Нам бы следовало завести козу — часть молока в пакетах оказалось с поврежденной упаковкой и испортилась, так что нам грозит молочный кризис…
***
Подняли спинакер. Оказалось, что мои представления о spinnaker trip для этой яхты слишком радикальны.
-…но подожди, я думала, условно говоря, я его отпускаю, пока он почти не сваливается, и тут даю команду grinfer’у крутить лебедку…
— ага, и так 5 тысяч миль? Мы все задолбаемся!
Короче, задача spinnaker trimmer’а на яхте «PSP Logictics»: ты сидишь со шкотом в руках и смотришь на парус. Если он вот уж прямо совсем падает и рулевой при этом не кричит «Извини, это я, не туда рулю, ща исправлюсь!» — то тогда trimmer, конечно, кричит ‘grind!! grind’ и один-два человека начинают активно крутить лебедку.
***
У нас в команде был товарищ из Ливана по имени Моисей — он должен был идти вокруг света, но в связи со смертью отца сошел на берег в Австралии. В связи с этим лучший диалог сезона:
— …Падди не испек хлеб! Завтра мне предстоит накормить одним хлебом семерых!
— А как насчет превращения воды (желательно морской) в вино?
— Может, тебе надо еще чтобы море расступилось и мы быстро докатили до Сиэтла?
— А вот для этого нам нужен Моисей…
День восьмой
Вчера мы перевыполнили программу по новым впечатлениям: дельфины, радуга, private jet береговой охраны Японии прилетел (низко-низко), покружил, связался по VHF с идущей впереди нас «Great Britain», расспросил, кто, куда, зачем, что за гонка, сколько нас таких, поблагодарил за сотрудничество и улетел.
Погоды стоят чудесные — тепло необычайно, мы разделись до шортов и маек (а я-то готовилась к снегу). Дошло до мытья головы на палубе.
***
Еще сегодня мой первый день в роли mother. Паникую, ничего не успеваю (за счет перевода часов у меня украли 2 часа времени, которых мне как раз не хватило, чтобы испечь хлеб). Команда, тем не менее, довольна.
С едой у нас, благодаря гениальным организаторским способностям Сью, все очень просто. Меню рассчитано на 8 дней, затем начинает повторяться. Замороженное мясо — в морозилках, остальные продукты на день разложены по пронумерованным гермомешкам: один мешок — один день. Утром берешь с полки мешок — там все, что нужно. Меню и инструкции — в специальной папке. Мне досталось приготовить на ужин «Cottage Pie». Я озадачилась — что бы это могло быть? Интернета нет — как готовить? Меня успокоили, рассказав, что это просто фарш с добавками, запеченый под слоем картофельного пюре, и вообще я вольна готовить что захочу из данного набора продуктов. Я обрадовалась, включила фантазию и приготовила что-то вроде рагу.
Ворчливый и вечно всем недовольный Алан, опустошив свою миску, кивает в мою сторону: «Вот человек знает, как готовить картофель!»
Я озадачена: а что, собственно, я сделала?
— Ты его *почистила*, прежде чем нарезать кусками!
Удалось мне также справиться и с десертом в пакетиках (что-то вроде пудинга), несмотря на то, что инструкции на пакетике были по-итальянски, а сверху была наклеена этикетка по-китайски…
Вместе с хлебом я обеспечила команду и зрелищами. Спускаясь с трапа (вторая смена заканчивает ужин, я передавала наверх кастрюлю с остатками еды — выкинуть за борт) я неудачно поворачиваюсь — и в левом колене раздается оглушительный (для меня, по крайней мере) хруст, а я издаю еще более громкий вопль. Дальше еще пару минут все у меня наперебой интересуются «что случилось», а я шиплю и через стиснутые зубы повторяю, что я в порядке, я в порядке, в порядке я, все нормально, могу ходить и стоять, жить буду.
И в самом деле — могу ходить и стоять. Колено будет болеть при прикосновениях до самого финиша, но, к счастью, совсем не мешать передвижениям.
***
Флотилия идет необычайно плотной группой. Восьмой день гонки, а мы все еще видим на горизонте лидеров турнирной таблицы — «LMAXю» и компанию.- Представляете, как переживают сейчас на «LMAX»:
— уже восьмой день гонки, а мы все еще в пределах видимости «PSP Logictics!»
— Кстати, знаешь кто сейчас лидирует? «Unicef»!
— Кто??!!! Умереть со смеха можно!
(Unicef традиционно финишировала одной из последних, но после предыдущего сегмента у них сменился шкипер — и потрясающе изменились результаты). Вот именно так, наверное, все реагировали, когда мы ненадолго выбились в лидеры. «Кто-кто лидирует?! PSP? Да не может быть, умора какая!»
***
Весь вечер не было ветра, тишина и покой, лодка никуда не кренится (очень удобно, закончив с мытьем посуды я переоделась в чистое, привела себя в порядок и вообще) — стоило мне устроиться поудобнее на койке с записной книжкой, как мы резко ускорились — аж уши заложило, яхта накренилась, с палубы донеслись крики («Reefing! Yankee 1 down! Get Yankee 3 on deck!*») и топот. А я-то хотела поспать…
===
* Headsails (они же, кажется, стаксели) нумеруются — от #1 (самый большой) до #4 (самый маленький). На Clipper 70 при этом используется специальный тип стакселей, именуемый Yankee — отличается он тем, что его шкотовый угол поднят довольно высоко. При усилении ветра, когда яхта оказывается overpowered, часто требуется сменить стаксель — поставить стаксель с большим номером (или вообще сбросить) — данное действие часто сопровождается криками, руганью и вообще нездоровой суетой.
Продолжение следует…
Оригинал опубликован в живом журнале Евгении Линковой
Фото автора и с сайта clipperroundtheworld.com
Отвод Э.С. 160 30 градусов
Отвод Э.С. 160 30 градусов предназначена для устройства поворота под углом 30 градусов полиэтиленовой (ПНД) трубы диаметром 160 мм при строительстве новых или ремонте уже существующих водопроводных и газовых систем.
Отвод Э.С. 160 30 градусов производится из полиэтилена высокого качества марки ПЭ100 SDR11 с использованием современных инновационных технологий работы с полимерными материалами. В процессе производства специальным методом электронагревательная спираль укладывается в тело отвода, благодаря чему, при ее нагреве происходит большая теплоотдача, что способствует качественному и равномерному расплавлению полиэтилена на внутренней поверхности отвода и внешней поверхности трубы по всей площади соприкосновения свариваемых частей.
На корпусе каждого фитинга имеется специальная наклейка со штрих кодом. В нем закодирована полная информация о производителе и параметрах сварки.
В параметры сварки входит:
- сила тока, необходимая для полного прогрева фитинга,
- время нагревания спирали,
- время необходимое для остывания и затвердевания свариваемых частей.,
- различные поправочные коэффициенты, учитывающие температуру окружающей среды, влажность и т.д.
Сварка производится специальным сварочным аппаратом, который имеет сканер для считывания информации со штрих кода, а также, память на определенное количество производимых сварок. Данная информация позже может быть распечатана и приложена к документации на производимый стык. Это часто требуется при сварке газовых магистралей, где необходим особый контроль качества.
Сварка отвода производится согласно стандартам и последовательности необходимой при сварке полиэтиленовых электросарных фитингов. Инструкцию по сварке муфт можно скачать здесь.
Отвод Э.С. 160 30 градусов — характеристики:
- Диаметр ПНД трубы — 160 мм;
- Угол поворота — 30º;
- Материал полиэтилен марки — ПЭ100 SDR11;
- Максимальное рабочее давление ВОДА — 16 атмосфер;
- Максимальное рабочее давление ГАЗ — 10 атмосфер;
- Максимальная рабочая температура — 40ºС;
- Страна производитель — Гемания;
- Вес — 3870 гр;
- Артикул — 615340-W30
Просмотры: 706
Как построить углы 30 °, 60 °, 90 ° и 120 °
Содержание
- Строительство уголков
- Как построить угол 90 градусов
- Как построить угол 60 градусов
- Этапы построения угла 60 градусов с помощью компаса
- Как построить угол 30 градусов
- Как построить угол в 120 градусов с помощью компаса
Конструкция уголков
Один из самых прекрасных аспектов геометрии — это то, насколько все аккуратно сочетается друг с другом.Знание того, как разделить отрезок пополам, означает, что мы знаем, как сделать угол 90 °. Зная, что у равностороннего треугольника есть три угла по 60 °, легко построить угол 60 °, используя только циркуль, карандаш и линейку. Все сочетается друг с другом. Вам понадобятся почти те же инструменты, которые использовал Евклид тысячи лет назад:
- Компас для рисования
- Линейка
- Карандаш
- Немного бумаги
Как построить угол 90 градусов
- На бумаге начертите отрезок линии длиннее луча под нужным вам углом 90 °.
- Найдите две точки на отрезке с обоих концов.
- Откройте циркуль для рисования, чтобы немного выйти за пределы половины отрезка линии (делайте это визуально; цифры не нужны).
- Прокрутите дугу над и под отрезком линии.
- Не меняя компас, переместите его на другую конечную точку.
- Проведите еще одну дугу над и под отрезком линии. Две дуги должны пересекаться выше и ниже отрезка линии.
Соединение точек пересечения дуги с помощью линейки создаст аккуратный, верный угол 90 °, при этом поперечная и исходная линия пересекаются под четырьмя прямыми углами!
Как построить угол 60 градусов
Что-то практически мистическое окружает 60 °.Он образует внутренние углы равносторонних треугольников. Это ровно 1/6 круга. Половина его плюс сама образует прямой угол. Вы можете продолжать и продолжать.
Этапы построения угла 60 градусов с помощью компаса
Создание угла 60 ° начинается с запоминания этого равностороннего треугольника.
- Постройте линейный сегмент с помощью линейки. Обозначьте его конечные точки. На нашем чертеже мы будем называть их точками O и G. [вставьте рисунок отрезка OG слева направо]
- Поместите стрелку циркуля для рисования в точку O и отрегулируйте ее так, чтобы она соответствовала точке G.
- Поверните дугу вверх от точки G выше отрезка линии.
- Не регулируя компас, переместите стрелку в точку G.
- Поверните дугу вверх, чтобы она пересекла первую дугу.
- Используйте линейку, чтобы построить отрезок от точки O до точки пересечения двух дуг.
- Обозначьте новую конечную точку этого линейного сегмента Точка D.
Угол, полученный от точек D до O и G при нанесении трех совпадающих длин, составляет 60 °.Если хотите, вы можете соединить точки D и G и образовать равносторонний треугольник. Эй, СОБАКА, у тебя получилось!
Как построить угол 30 градусов
Угол 30 ° равен половине угла 60 °. Итак, чтобы нарисовать 30 °, постройте угол 60 °, а затем разделите его пополам.
Сначала выполните указанные выше действия, чтобы построить угол 60 °.
Разделите угол 60 ° пополам с помощью циркуля для рисования, например:
- Не меняя компаса, переместите иглу в одну из точек на лучах.Проведите дугой внутри уголка.
- Не меняя компаса, переместите иглу к точке другого луча. Проведите дугой внутри уголка.
- Используйте линейку, чтобы соединить пересечение двух дуг с вершиной угла 60 °. Этот отрезок представляет собой биссектрису угла, что дает два угла по 30 °.
Как построить угол в 120 градусов с помощью компаса
Помните, как мы говорили, что в геометрии все сочетается друг с другом? Какой дополнительный угол к углу 120 °? Другими словами, какой угол мы должны добавить к 120 °, чтобы получить 180 °?
Вы сказали 60 °? Конечно, угол 120 ° — это угол, примыкающий к любому из уже построенных вами углов в 60 °!
Чтобы построить угол 120 °, постройте угол 60 °, а затем вытяните одну из его сторон далеко за вершину, например:
[вставьте анимацию с построенным углом 60 °, затем проведите по краю и выделите примыкающий к нему угол 120 °]
Угол, превышающий 60 °, составляет ваш угол 120 °.
Ни одна из ваших конструкций не требует чисел или размеров. Евклид гордился бы тобой!
Следующий урок:
Построение равностороннего треугольника
Измерение углов
Измерение углов
Понятие угла
Понятие угла — одно из важнейших понятий в геометрии. Понятия равенства, суммы и разности углов важны и используются во всей геометрии, но предмет тригонометрии основан на измерении углов .
Есть две обычно используемые единицы измерения углов. Более знакомая единица измерения — это градусы. Круг делится на 360 равных градусов, так что прямой угол равен 90 °. Пока мы будем рассматривать только углы от 0 ° до 360 °, но позже, в разделе о тригонометрических функциях, мы будем рассматривать углы больше 360 ° и отрицательные углы. Градусы можно разделить на минуты и секунды, но это деление не так универсально, как раньше.Каждый градус делится на 60 равных частей, называемых минут. Итак, семь с половиной градусов можно назвать 7 градусами и 30 минутами, записанными как 7 ° 30 ‘. Каждая минута далее делится на 60 равных частей, называемых секунд, и, например, 2 градуса 5 минут 30 секунд записывается как 2 ° 5 ’30 «. Деление градусов на минуты и угловые секунды аналогично делению на часы в минуты и секунды. |
Части градуса теперь обычно обозначаются десятичной дробью.Например, семь с половиной градусов теперь обычно пишут как 7,5 & deg.
Когда один угол нарисован на плоскости xy для анализа, мы нарисуем его в стандартной позиции с вершиной в начале координат (0,0), одна сторона угла вдоль x ось, а другая сторона выше оси x .
Радианы
Другое распространенное измерение углов — радианы.Для этого измерения рассмотрим единичный круг (круг радиуса 1), центр которого является вершиной рассматриваемого угла. Затем угол отсекает дугу окружности, и длина этой дуги является мерой угла в радианах. Легко переходить между градусами и радианами. Длина окружности всего круга равна 2 π , следовательно, 360 ° равняется 2 π радиан. Следовательно, 1 ° равняется π /180 радиан а также 1 радиан равен 180/ π градус Большинство калькуляторов можно настроить на использование углов, измеряемых в градусах или радианах.Убедитесь, что вы знаете, в каком режиме работает ваш калькулятор. |
Краткая заметка об истории радианов
Хотя слово «радиан» было придумано Томасом Мьюром и / или Джеймсом Томпсоном около 1870 года, математики долгое время измеряли углы таким способом. Например, Леонард Эйлер (1707–1783) в своей работе Elements of Algebra явно сказал, что углы следует измерять по длине дуги, отрезанной в единичной окружности.Это было необходимо, чтобы дать его знаменитую формулу, включающую комплексные числа, которая связывает функции знака и косинуса с экспоненциальной функцией.
e iθ = cos θ + i sin θ
где θ — это то, что позже было названо измерением угла в радианах. К сожалению, объяснение этой формулы выходит далеко за рамки этих заметок. Но для получения дополнительной информации о комплексных числах см. Мой Краткий курс комплексных чисел.
Радианы и длина дуги
Альтернативное определение радианов иногда дается в виде отношения. Вместо того, чтобы брать единичную окружность с центром в вершине угла θ , возьмите любую окружность с центром в вершине угла. Тогда радианная мера угла — это отношение длины вытянутой дуги к радиусу r окружности. Например, если длина дуги равна 3, а радиус окружности равен 2, тогда мера в радианах равна 1.5.
Причина, по которой это определение работает, заключается в том, что длина вытянутой дуги пропорциональна радиусу круга. В частности, определение в терминах отношения дает ту же цифру, что и приведенная выше с использованием единичного круга. Однако это альтернативное определение более полезно, поскольку вы можете использовать его для соотнесения длин дуг с углами. Длина дуги равна радиусу r, умноженному на угол θ , где угол измеряется в радианах.
Например, дуга θ = 0,3 радиана в окружности радиуса r = 4 имеет длину 0,3 умноженную на 4, то есть 1,2.
Радианы и площадь сектора
Сектор круга — это часть круга, ограниченная двумя радиусами и дугой круга, соединяющей их концы. Площадь этого сектора легко вычислить по радиусу r окружности и углу θ между радиусами, когда он измеряется в радианах.Так как площадь всего круга составляет πr 2 , а сектор относится к всей окружности, так как угол θ равен 2 π , поэтому
Углы общие
Ниже приведена таблица общих углов как при измерении в градусах, так и при измерении радиан. Обратите внимание, что измерение в радианах дано в терминах π . Его, конечно, можно было бы указать в десятичной дроби, но радианы часто появляются с коэффициентом π
.
| Уголок | Градусов | Радианы |
|---|---|---|
| 90 ° | π /2 | |
| 60 ° | π /3 | |
| 45 ° | π /4 | |
| 30 ° | π /6 |
Упражнения
Эдвин С.Кроули написал книгу Тысяча упражнений в плоской и сферической тригонометрии, Университет Пенсильвании, Филадельфия, 1914. Задачи этого короткого курса взяты из этого текста (но не все 1000 из них!). пять знаков точности, поэтому студентам пришлось потрудиться, чтобы решить их, и они использовали таблицы логарифмов, чтобы помочь в умножении и делении. Студенты должны были уметь пользоваться таблицей синус-косинусов, таблицей касательных, таблицей логарифмов, таблицей log-sin-cos и таблицей log-tan.Теперь мы можем пользоваться калькуляторами! Это означает, что вы можете сосредоточиться на концепциях, а не на трудоемких вычислениях.
Кроули использовал не десятичные дроби градуса, а минуты и секунды.
Каждый комплекс упражнений включает в себя, во-первых, формулировку упражнений, во-вторых, некоторые подсказки для решения упражнений, а в-третьих, ответы на упражнения.
1. Выразите следующие углы в радианах.
(а). 12 градусов, 28 минут, то есть 12 ° 28 ‘.
(б). 36 ° 12 ‘.
2. Сократите следующие числа радианов до градусов, минут и секунд.
(а). 0,47623.
(б). 0,25412.
3. Учитывая угол a и радиус r, , чтобы найти длину продолжающейся дуги.
(а). a = 0 ° 17 ’48 дюймов, r = 6,2935.
(б). a = 121 ° 6 ’18 дюймов, r = 0,2163.
4. Учитывая длину дуги l и радиус r, , чтобы найти угол, стянутый в центре.
(а). л = 0,16296, л = 12,587.
(б). л = 1,3672, л = 1,2978.
5. Зная длину дуги l и угол a , который она проходит в центре, найти радиус.
(а). a = 0 ° 44 ’30 дюймов, l = 0,032592.
(б). a = 60 ° 21 ‘6 дюймов, l = 0,4572.
6. Найдите длину с точностью до дюйма дуги окружности 11 градусов 48,3 минуты, если радиус 3200 футов.
7. Кривая железной дороги образует дугу окружности 9 градусов 36,7 минут, радиус до центральной линии пути составляет 2100 футов. Если калибр 5 футов, найдите разницу в длине двух рельсов с точностью до полудюйма.
9. Насколько можно изменить широту, идя на север на одну милю, если предположить, что Земля представляет собой сферу радиусом 3956 миль?
10. Вычислите длину в футах одной угловой минуты на большом круге Земли. Какова длина дуги в одну секунду?
14. На окружности радиусом 5,782 метра длина дуги составляет 1,742 метра. Какой угол он образует в центре?
23. Воздушный шар, известный как 50 футов в диаметре, сужается к глазу под углом 8 1/2 минут.Как далеко это?
Подсказки
1. Чтобы преобразовать градусы в радианы, сначала преобразуйте количество градусов, минут и секунд в десятичную форму. Разделите количество минут на 60 и прибавьте к количеству градусов. Так, например, 12 ° 28 ‘равно 12 + 28/60, что равно 12,467 °. Затем умножьте на π и разделите на 180, чтобы получить угол в радианах.
2. И наоборот, чтобы преобразовать радианы в градусы, разделите на π и умножьте на 180.Таким образом, 0,47623, деленное на π и умноженное на 180, дает 27,286 °. Вы можете преобразовать доли градуса в минуты и секунды следующим образом. Умножьте дробь на 60, чтобы получить количество минут. Здесь 0,286 умножить на 60 равно 17,16, поэтому угол можно записать как 27 ° 17,16 ‘. Затем возьмите любую оставшуюся долю минуты и снова умножьте на 60, чтобы получить количество секунд. Здесь 0,16 умножить на 60 равно примерно 10, поэтому угол также можно записать как 27 ° 17 ’10 дюймов.
3. Чтобы найти длину дуги, сначала преобразуйте угол в радианы. Для 3 (a) 0 ° 17’48 «равно 0,0051778 радиан. Затем умножьте его на радиус, чтобы найти длину дуги.
4. Чтобы найти угол, разделите его на радиус. Это дает вам угол в радианах. Их можно преобразовать в градусы, чтобы получить ответы Кроули.
5. Как упоминалось выше, радиан умноженный на радиус = длина дуги, поэтому, используя буквы для этой задачи, ar = l, , но a необходимо сначала преобразовать из градусного измерения в радиан .Итак, чтобы найти радиус r, сначала преобразует угол a в радианы, а затем разделит его на длину l дуги.
6. Длина дуги равна радиусу, умноженному на угол в радианах.
7. Помогает нарисовать фигуру. Радиус внешнего рельса равен 2102,5, а радиус внутреннего рельса — 2097,5.
9. У вас получился круг радиусом 3956 миль и дуга этого круга длиной 1 милю.Какой угол в градусах? (Средний радиус Земли был известен довольно точно в 1914 году. Посмотрим, сможете ли вы узнать, каким, по мнению Эратосфена, был радиус Земли, еще в III веке до н. Э.)
10. Угловая минута равна 1/60 градуса. Преобразовать в радианы. Радиус — 3956. Какова длина дуги?
14. Поскольку длина дуги равна радиусу, умноженному на угол в радианах, отсюда следует, что угол в радианах равен длине дуги, деленной на радиус.Радианы легко преобразовать в градусы.
23. Представьте, что диаметр воздушного шара является частью дуги окружности с вами в центре. (Это не совсем часть дуги, но довольно близко). Длина дуги составляет 50 футов. Вы знаете угол, так каков радиус этого круга?
ответы
1. (а). 0,2176. (б). 0,6318.
2. (а). 27 ° 17 ’10 «. (B). 14,56 ° = 14 ° 33,6′ = 14 ° 33’36».
3. (а). 0,03259 (б). 2,1137 умножить на 0,2163 равно 0,4572.
4. (а). 0,16296 / 12,587 = 0,012947 радиан = 0 ° 44 ’30 дюймов.
(б). 1,3672 / 1,2978 = 1,0535
радианы = 60,360 ° = 60 ° 21,6 ‘= 60 ° 21’ 35 «.
5. (а). л / год = 0,032592 / 0,01294 = 2,518.
(б). л / год = 0,4572 / 1,0533 = 0,4340.
6. ra = (3200 ‘) (0.20604) = 659,31 ‘= 659’ 4 дюйма.
7. Угол a = 0,16776 радиана. Разница в длине составляет
2102,5 a — 1997,5 a , что составляет 5 a. Таким образом, ответ составляет 0,84 фута, что с точностью до дюйма составляет 10 дюймов.
9. Угол = 1/3956 = 0,0002528 радиан = 0,01448 ° = 0,8690 ‘= 52,14 дюйма.
10. Одна минута = 0,0002909 радиан. 1.15075 миль = 6076 футов.Следовательно, одна секунда будет соответствовать 101,3 фута.
14. a = л / об = 1,742 / 5,782 = 0,3013 радиан = 17,26 ° = 17 ° 16 ‘.
23. Угол a равен 8,5 ‘, что составляет 0,00247 радиана. Таким образом, радиус равен r = л / год = 50 / 0,00247 = 20222 ‘= 3,83 мили, почти четыре мили.
Насчет цифр точности.
Кроули старается давать свои ответы примерно с той же точностью, что и данные в вопросах.Это важно, особенно сейчас, когда у нас есть калькуляторы. Например, в задаче 1 точка отсчета равна 12 ° 28 ‘, что соответствует примерно четырем знакам точности, поэтому ответ 0,2176 также должен быть дан только с точностью до четырех знаков. (Обратите внимание, что ведущие нули не учитываются при вычислении цифр точности.) Ответ 0,21758438 предполагает восемь цифр точности, и это будет вводить в заблуждение, поскольку данная информация не была такой точной.
Другой пример см. В задаче 3 (a). Данные 0 ° 17’48 «и 6.2935 с точностью до 4 и 5 знаков соответственно. Следовательно, ответ должен быть дан только с точностью до 4 цифр, так как ответ не может быть более точным, чем наименее точные данные. Таким образом, ответ, который может дать калькулятор, а именно 0,032586547, следует округлить до четырех цифр (не включая ведущие нули) до 0,03259.
Хотя окончательные ответы должны быть выражены с соответствующим числом цифр точности, вы все равно должны сохранять все цифры для промежуточных вычислений.
Углы складывания 30 и 60 градусов — Британское общество оригами
Для тех из нас, кто регулярно складывает бумагу, создание углов 90o и 45o — почти вторая натура. Мы создаем прямой угол, складывая край или складку обратно на себя, и мы можем разделить прямой угол (или любой другой угол) пополам, соединив складки / края, которые образуют два плеча угла, и сгибая их между собой. их. Математику углов складывания 60o или 30o понять немного сложнее.(Другие углы, которые часто необходимо создавать для бумажных папок, особенно модульных папок, — это углы 108 и 72 градуса, которые полезны при создании многогранников с пятиугольными гранями и других связанных форм.)
Метод построения углов 60o и 30o путем складывания основан на симметрии равностороннего треугольника — треугольника с тремя сторонами равной длины. Чтобы пояснение было ясным, мы будем использовать в качестве примера равносторонний треугольник с ребрами длиной 2 единицы. Нам нужно посмотреть только на половину.
Самый длинный край прямоугольного треугольника, который составляет половину равностороннего треугольника — его гипотенуза на языке геометрии — является одним из ребер исходного треугольника и, следовательно, имеет длину 2 единицы. Самый короткий край треугольника — внизу диаграммы — равен половине длины одного из исходных ребер и, следовательно, имеет длину 1 единицу. Это соотношение 2: 1 этих кромок с прямым углом на конце
самого короткого края, является ключом к построению углов 60o и 30o путем складывания бумаги.(Для тех из вас, кто знаком с евклидовой геометрией, это треугольник, описываемый условием «прямой угол, гипотенуза и сторона», что является условием конгруэнтности.) На схемах ниже показан классический способ сложить угол 60o в плоскости середина верхнего края прямоугольника. Для этого сначала согните бумагу пополам, чтобы отметить центральную линию, затем согните правый край к центральной линии, чтобы согнуть правую половину бумаги на две четверти. (Посмотрите на первую диаграмму — это проще!) Чтобы сформировать угол 60o, поверните верхний левый угол до четверти сгиба, убедившись, что сгиб начинается на центральной линии.
Заштрихованный треугольник на правой диаграмме выше является примером равностороннего треугольника, описанного выше. У него самый длинный край — гипотенуза — половина длины верхнего края бумаги, самый короткий край, равный четверти длины верхнего края бумаги, и прямой угол на конце самого короткого края. Это создает соотношение 2: 1 (с прямым углом на конце кратчайшего края), которое мы ищем.
Тот факт, что угол заштрихованного треугольника в центре верхнего края равен 60o, означает, что угол рядом с ним по краю (его дополнению) равен 120o, и он делится пополам на сгиб, который мы сделали.Сгибая правый верхний угол так, чтобы он лежал вдоль первого загнутого края, мы можем создать три равных угла, каждый по 60o, в центре верхнего края прямоугольника.
Складываем другой (правый) угол поперек так, чтобы две необработанные кромки лежали вместе, делит пополам угол 60 ° справа на два угла по 30 ° каждый. Конечно, нам не обязательно сначала делать угол 60o: мы можем просто повернуть правый верхний угол в четверть угла (третья диаграмма ниже). И снова заштрихованный треугольник имеет решающее соотношение 2: 1 между его самым длинным и самым коротким краями, с прямым углом на конце самого короткого края.На этот раз угол в заштрихованном треугольнике в центре верхнего края равен 30o, поэтому угол рядом с ним, вдоль края справа (его дополнения), равен 60o, который делится пополам сгибом.
С небольшими изменениями этих идей мы можем сложить угол 60o или 30o в углу или в центре квадрата, например:
Ян Харрисон
30 60 90 Правые треугольники
Треугольник особого вида
Прямоугольный треугольник 30-60-90 (буквально произносится как «тридцать шестьдесят девяносто») — это особый тип прямоугольного треугольника, в котором три угла составляют 30 градусов, 60 градусов и 90 градусов.Треугольник важен, потому что стороны существуют в легко запоминающемся соотношении: 1: \ (\ sqrt {3} \): 2. То есть гипотенуза в два раза длиннее более короткого отрезка, а более длинное отрезок представляет собой квадратный корень из 3-кратного более короткого отрезка. Вы также можете вспомнить это как «корни X, 2X и X из 3», как я его помню, но тогда вы должны помнить, что на самом деле самая длинная сторона — это 2X, а не корни X из 3.
Какая сторона какая? Сторона, противоположная углу 30 градусов, будет иметь наименьшую длину.Сторона, противоположная углу 60 градусов, будет в \ (\ sqrt {3} \) раз длиннее, а сторона, противоположная углу 90 градусов, будет вдвое длиннее. Треугольник ниже показывает эту взаимосвязь. Помните, что самая длинная сторона будет напротив самого большого угла, а самая короткая — напротив самого маленького угла.
Мы можем использовать соотношение между углами и сторонами треугольника 30-60-90, чтобы найти недостающие углы или длины сторон. Взгляните на этот пример:
Пример 1
Для треугольника 30-60-90 ниже найдите длины недостающих сторон:
Поскольку это прямоугольный треугольник 30-60-90, мы знаем, что стороны существуют в пропорции 1: \ (\ sqrt {3} \): 2.Самая короткая сторона, 1, находится напротив угла 30 градусов. Поскольку сторона X противоположна углу в 60 градусов, мы знаем, что он равен \ (1 * \ sqrt {3} \), или примерно 1,73. Наконец, сторона Y противоположна прямому углу, и это в два раза короче сторона, или 2.
Откуда взялась формула?
Это еще одна выдуманная математическая формула? Нет! Это просто приложение базовой тригонометрии. В приведенном выше примере мы могли бы взять синус крайнего левого угла: sin (30) = 1/2.Поскольку синус дает нам отношение противоположности к гипотенузе, мы бы знали, что гипотенуза должна быть 2. По сути, вся причина, по которой треугольник 30-60-90 легко решить, заключается в том, что синус и косинус этих углов равны тоже очень простой.
Пример 2
Используйте те же принципы для поиска неизвестных переменных X и Y.
Известная сторона — 4, и это самая длинная сторона. Помните, как длинная сторона в два раза длиннее самой короткой стороны для треугольника 30-60-90? Это означает, что Y должно быть 2!
Теперь мы можем найти оставшуюся сторону.Поскольку сторона , противоположная углу в 60 градусов, равна умножению более короткой стороны на квадратный корень из 3 , мы можем вычислить, что X равно \ (2 * \ sqrt {3} \).
Сводка
Для прямоугольного треугольника с углами 30, 60 и 90 градусов, стороны будут иметь длину в соотношении 1: \ (\ sqrt {3} \): 2, как показано на этой диаграмме:
Дополнительная справка
Как всегда, вы можете задать свои конкретные вопросы на нашей доске сообщений справки по математике, выполнить поиск в Google или пройти этот урок по 30-60-90 треугольникам или этот.Или, чтобы вычислить стороны и углы треугольника, используйте интерактивный инструмент ниже:
Простое руководство к треугольнику 30-60-90
Острый, тупой, равнобедренный, равносторонний… Когда дело доходит до треугольников, существует множество различных разновидностей, но лишь немногие из них являются «особенными». У этих специальных треугольников есть стороны и углы, которые согласованы и предсказуемы, и их можно использовать, чтобы сократить ваш путь через геометрические или тригонометрические задачи.И треугольник 30-60-90 — произносится как «тридцать шестьдесят девяносто» — действительно оказывается очень особенным типом треугольника.
В этом руководстве мы расскажем, что такое треугольник 30-60-90, почему он работает и когда (и как) использовать свои знания о нем. Итак, приступим!
Что такое треугольник 30-60-90?
Треугольник 30-60-90 — это специальный прямоугольный треугольник (прямоугольный треугольник — это любой треугольник, который содержит угол 90 градусов), который всегда имеет углы градусов 30 градусов, 60 градусов и 90 градусов.Поскольку это особый треугольник, у него также есть значения длины стороны, которые всегда находятся в постоянном соотношении друг с другом.
Базовое соотношение треугольника 30-60-90:
Сторона, противоположная углу 30 °: $ x $
Сторона, противоположная углу 60 °: $ x * √3 $
Сторона, противоположная углу 90 °: 2 доллара x
доллар США
Например, треугольник 30-60-90 градусов может иметь длину стороны:
2, 2√3, 4
7, 7√3, 14
√3, 3, 2√3
(Почему более длинная часть 3? В этом треугольнике самая короткая часть ($ x $) равна $ √3 $, поэтому для более длинной ветви $ x√3 = √3 * √3 = √9 = 3 $.А гипотенуза — это 2 кратчайшего отрезка, или 2√3 $)
И так далее.
Сторона, противоположная углу 30 °, всегда является наименьшим , потому что 30 ° — наименьший угол. Сторона, противоположная углу 60 °, будет средней длиной , потому что 60 градусов — это средний угол в этом треугольнике. И, наконец, сторона, противоположная углу 90 °, всегда будет самой большой стороной (гипотенуза) , потому что 90 градусов — это наибольший угол.
Хотя треугольник 30-60-90 может выглядеть так же, как другие типы прямоугольных треугольников, он настолько особенный, что вам нужно всего три части информации, чтобы найти любое другое измерение. Пока вы знаете значение двух угловых мер и длины одной стороны (не имеет значения, с какой стороны), вы знаете все, что вам нужно знать о своем треугольнике.
Например, мы можем использовать формулу треугольника 30-60-90, чтобы заполнить все оставшиеся информационные поля треугольников ниже.
Пример 1
Мы видим, что это прямоугольный треугольник, в котором гипотенуза вдвое больше длины одного из катетов. Это означает, что это должен быть треугольник 30-60-90, а меньшая заданная сторона противоположна 30 °.
Следовательно, более длинная полка должна располагаться напротив угла 60 ° и иметь размер 6 * √3 $ или 6√3 $.
Пример 2
Мы видим, что это должен быть треугольник 30-60-90, потому что мы видим, что это прямоугольный треугольник с одним заданным размером 30 °.Тогда немаркированный угол должен составлять 60 °.
Поскольку 18 — это мера, противоположная углу 60 °, она должна быть равна $ x√3 $. Тогда самая короткая ветка должна иметь размер 18 долл. США / √3 долл. США.
(Обратите внимание, что длина отрезка на самом деле будет $ 18 / {√3} * {√3} / {√3} = {18√3} / 3 = 6√3 $, потому что знаменатель не может содержать радикал / квадратный корень) .
А гипотенуза будет 2 (18 / √3) $
(Обратите внимание, что, опять же, у вас не может быть радикала в знаменателе, поэтому окончательный ответ действительно будет в 2 раза больше длины ножки $ 6√3 $ => $ 12√3 $).
Пример 3
Опять же, нам даны два измерения угла (90 ° и 60 °), поэтому третье измерение будет 30 °. Поскольку это треугольник 30-60-90, а гипотенуза равна 30, самый короткий отрезок будет равен 15, а более длинный отрезок будет равен 15√3.
Не нужно обращаться к волшебному шару-восьмерке — эти правила работают всегда.
Почему это работает: 30-60-90 Доказательство теоремы о треугольнике
Но почему этот особый треугольник работает именно так? Как мы узнаем, что эти правила законны? Давайте подробно рассмотрим, как работает теорема треугольника 30-60-90, и докажем, почему эти длины сторон всегда будут согласованными.
Во-первых, давайте на секунду забудем о прямоугольных треугольниках и посмотрим на равносторонний треугольник .
Равносторонний треугольник — это треугольник, у которого все стороны и углы равны. Поскольку внутренние углы треугольника всегда составляют в сумме 180 ° и $ 180/3 = 60 $, равносторонний треугольник всегда будет иметь три угла по 60 °.
Теперь давайте опустимся на высоту от самого верхнего угла до основания треугольника.
Теперь у нас созданы два прямых угла и два равных (равных) треугольника.
Откуда мы знаем, что это равные треугольники? Поскольку мы сбросили высоту из равностороннего треугольника , мы разделили основание ровно пополам. Новые треугольники также имеют одну длину стороны (высоту), и каждый из них имеет одинаковую длину гипотенузы. Поскольку у них три общих длины стороны (SSS), это означает, что треугольники совпадают.
Примечание: два треугольника совпадают не только на основе принципов длины стороны-стороны, или SSS, но также на основе измерений стороны-угла-стороны (SAS), угла-угла-стороны (AAS) и угла. -угловой (ASA).По сути? Они определенно совпадают.
Теперь, когда мы доказали конгруэнтность двух новых треугольников, мы видим, что каждый из верхних углов должен быть равен 30 градусам (потому что каждый треугольник уже имеет углы 90 ° и 60 ° и в сумме должно составлять 180 °). . Это означает, что мы сделали два треугольника 30-60-90.
И поскольку мы знаем, что мы разрезаем основание равностороннего треугольника пополам, мы можем видеть, что сторона, противоположная углу 30 ° (самая короткая сторона) каждого из наших треугольников 30-60-90, составляет ровно половину длины треугольника. гипотенуза.2} / 4
долл. США
долл. США b = {√3x} / 2
долл. США
Итак, у нас осталось: $ x / 2, {x√3} / 2, x $
Теперь давайте умножим каждую меру на 2, чтобы облегчить жизнь и избежать использования дробей. Таким образом, у нас осталось:
$ x $, $ x√3 $, 2x $
Таким образом, мы можем видеть, что треугольник 30-60-90 всегда будет иметь одинаковую длину сторон $ x $, $ x√3 $ и $ 2x $ (или $ x / 2 $, $ {√3x } / 2 $ и $ x $).
К счастью для нас, мы можем доказать, что правила треугольника 30-60-90 верны без всего этого…это.
Когда использовать правила треугольника 30-60-90
Знание правил треугольника 30-60-90 поможет вам сэкономить время и силы при решении множества различных математических задач, а именно, большого разнообразия задач по геометрии и тригонометрии.
Геометрия
Правильное понимание треугольников 30-60-90 позволит вам решать вопросы геометрии, которые либо невозможно решить, не зная этих правил соотношения, либо, по крайней мере, потребуется значительное время и усилия для решения «долгого пути».«
С помощью специальных соотношений треугольников вы можете вычислить недостающие высоты или длины участков треугольника (без использования теоремы Пифагора), найти площадь треугольника, используя недостающую информацию о высоте или базовой длине, и быстро вычислить периметры.
Каждый раз, когда вам нужна скорость, чтобы ответить на вопрос, вам пригодятся такие ярлыки, как правила 30-60-90.
Тригонометрия
Запоминание и понимание соотношения треугольников 30-60-90 также позволит вам решать многие тригонометрические задачи без использования калькулятора или необходимости приближать ваши ответы в десятичной форме.
Треугольник 30-60-90 имеет довольно простые синусы, косинусы и тангенсы для каждого угла (и эти измерения всегда будут согласованы).
Синус 30 ° всегда будет $ 1/2 $.
Косинус 60 ° всегда будет $ 1/2 $.
Хотя другие синусы, косинусы и касательные довольно просты, их легче всего запомнить, и они, вероятно, обнаружатся на тестах. Таким образом, знание этих правил позволит вам как можно быстрее найти эти тригонометрические измерения.
Советы по запоминанию правил 30-60-90
Вы знаете, что эти правила соотношения 30-60-90 полезны, но как вы удерживаете информацию в своей голове? Чтобы помнить правила треугольника 30-60-90, нужно помнить о соотношении 1: √3: 2 и знать, что длина самой короткой стороны всегда противоположна самому короткому углу (30 °), а длина самой длинной стороны всегда противоположна наибольший угол (90 °).
Некоторые люди запоминают соотношение, думая: « $ \ bi x $, $ \ bo 2 \ bi x $, $ \ bi x \ bo √ \ bo3 $, », потому что последовательность «1, 2, 3» обычно легко запомнить. Единственная мера предосторожности при использовании этого метода — помнить, что самая длинная сторона на самом деле — это $ 2x $, не , а $ x $ умноженное на $ √3 $.
Другой способ запомнить ваши отношения — это использовать мнемоническую игру слов на соотношении 1: корень 3: 2 в их правильном порядке. Например, «Джеки Митчелл выбил Лу Герига и« выиграл и Рути тоже »»: один, корень три, два. (И это, кстати, реальный факт из истории бейсбола!)
Поиграйте со своими собственными мнемоническими устройствами, если они вам не нравятся — спойте отношение к песне, найдите свои собственные фразы «один, корень три, два» или придумайте стихотворение о соотношении.Вы даже можете просто запомнить, что треугольник 30-60-90 — это половина равносторонней стороны, и вычислить оттуда размеры, если вам не нравится их запоминать.
Однако для вас имеет смысл запомнить эти правила 30-60-90, держите эти соотношения в уме для будущих вопросов по геометрии и тригонометрии.
Запоминание — ваш друг, однако вы можете сделать это возможным.
Ваша школа сообщает ваш средний балл как взвешенный или невзвешенный? Каким будет ваш средний балл, с учетом 4.Шкала 0, 5.0 или 6.0? Воспользуйтесь нашим инструментом, чтобы рассчитать свой невзвешенный и взвешенный средний балл успеваемости, чтобы выяснить, как вы соотноситесь с другими абитуриентами. Вы также получите наш собственный расчет среднего балла среднего балла колледжа и советы о том, где можно улучшить, чтобы стать лучшим поступающим в колледж.
Пример 30-60-90 Вопросы
Теперь, когда мы рассмотрели «как» и «почему» 30-60-90 треугольников, давайте поработаем над некоторыми практическими задачами.
Геометрия
Строитель прислоняет 40-футовую лестницу к стене здания под углом 30 градусов от земли.Земля ровная, а сторона здания перпендикулярна земле. Как далеко вверх по зданию до ближайшего подножия поднимается лестница?
Не зная наших специальных правил треугольника 30-60-90, нам пришлось бы использовать тригонометрию и калькулятор, чтобы найти решение этой проблемы, поскольку у нас есть только одно измерение стороны треугольника. Но поскольку мы знаем, что это особый треугольник , мы можем найти ответ за считанные секунды.
Если здание и земля перпендикулярны друг другу, это должно означать, что здание и земля образуют прямой (90 °) угол.Также известно, что лестница встречается с землей под углом 30 °. Таким образом, мы видим, что оставшийся угол должен составлять 60 °, что составляет треугольник 30-60-90.
Теперь мы знаем, что гипотенуза (самая длинная сторона) 30-60-90 составляет 40 футов, а это означает, что самая короткая сторона будет вдвое меньше. (Помните, что самая длинная сторона всегда вдвое длиннее — $ 2x $ — самой короткой стороны.) Поскольку самая короткая сторона находится напротив угла 30 °, и этот угол является мерой лестницы от земли в градусах, это означает, что верхняя часть лестницы ударяется о здание на высоте 20 футов от земли.
Наш окончательный ответ — 20 футов.
Тригонометрия
Если в прямоугольном треугольнике sin Θ = $ 1/2 $, а длина самого короткого участка равна 8. Какова длина недостающей стороны, НЕ являющейся гипотенузой?
Так как вы знаете свои правила 30-60-90, вы можете решить эту проблему без использования теоремы Пифагора или калькулятора.
Нам сказали, что это прямоугольный треугольник, и мы знаем из наших специальных правил прямоугольного треугольника, что синус 30 ° = $ 1/2 $.Следовательно, недостающий угол должен составлять 60 градусов, что делает треугольник 30-60-90.
И поскольку это треугольник 30-60-90, и нам сказали, что самая короткая сторона равна 8, гипотенуза должна быть равна 16, а недостающая сторона должна быть $ 8 * √3 $ или 8√3 $.
Наш окончательный ответ — 8√3.
Итоги
Запоминание правил для треугольников 30-60-90 поможет вам сократить свой путь через множество математических задач .Но имейте в виду, что, хотя знание этих правил — удобный инструмент, который нужно держать на поясе, вы все равно можете решить большинство проблем без них.
Следите за правилами $ x $, $ x√3 $, $ 2x $ и 30-60-90 любым понятным для вас образом и старайтесь придерживаться их, если можете, но не паникуйте, если вы ум исчезает, когда наступает время кризиса. В любом случае, у вас есть это.
И, если вам нужно больше практики, попробуйте эту викторину с треугольником 30-60-90. Удачной сдачи теста!
Веб-сайт класса физики
Максимальный диапазон
Представьте себе пушечное ядро, выпущенное из пушки под тремя разными углами пуска — 30 градусов, 45 градусов и 60 градусов.Скорость запуска поддерживается постоянной; меняется только угол. Представьте также, что ядра не испытывают значительного сопротивления воздуха. Как будут сравниваться траектории трех пушечных ядер? Какое ядро будет иметь наибольшую дальность действия? Какое ядро перед падением достигнет максимальной высоты пика? Какое ядро первым коснется земли? На анимации ниже изображена такая ситуация. Показан путь пушечных ядер. Кроме того, компоненты скорости (горизонтальная и вертикальная) представлены стрелками в анимации.
Как видно из приведенной выше анимации, каждое пушечное ядро следует параболической траектории. Пушечное ядро, выпущенное под углом 45 градусов, имело наибольшую дальность действия. Пушечное ядро, выпущенное под углом 60 градусов, имело наибольшую высоту пика перед падением. Пушечное ядро, выпущенное под углом 30 градусов, первым достигло земли.
Анализ составляющих скорости этих трех снарядов раскрывает причины этих наблюдений. Пиковая высота снаряда определяется начальным значением вертикальной составляющей скорости.Чем больше начальное значение v y , тем выше поднимется снаряд. Снаряд, выпущенный под углом 60 градусов, имеет наибольшее v y и, следовательно, наибольшую высоту пика. «Время зависания» снаряда также определяется начальным значением вертикальной составляющей скорости. Чем меньше начальное значение v y , тем короче время зависания. Снаряд, выпущенный под углом 30 градусов, имеет наименьшие v y и, следовательно, самое короткое время зависания. Дальность полета снаряда определяется двумя параметрами — начальным значением горизонтальной составляющей скорости и временем зависания снаряда.Как видно из анимации, наибольшее время зависания имеет снаряд, выпущенный под углом 60 градусов; однако его диапазон ограничен тем фактом, что v x — самый маленький из всех трех углов. Снаряд, выпущенный под углом 30 градусов, имеет наибольший v x из всех трех углов пуска; однако его диапазон ограничен тем фактом, что время зависания очень короткое. Снаряд, выпущенный под углом 45 градусов, не дает победы ни в одной из категорий , но тот факт, что он способен занять сильное место в каждой категории , помогает ему достичь максимальной дальности.Существуют более изощренные аргументы в пользу того, почему угол запуска в 45 градусов дает наибольшую дальность полета; тем не менее, поскольку они связаны с исчислением, они здесь не представлены.
Для получения дополнительной информации о физических описаниях движения посетите The Physics Classroom Tutorial. Подробная информация доступна по следующим темам:
Снаряды
Характеристики траектории снаряда
Описание снарядов с номерами
Начальные компоненты скорости
Свойства прямоугольного треугольника при угле 30 °
Недвижимость
В прямоугольном треугольнике, когда его угол равен 30 градусам, можно выделить три основных свойства.° $. Предположим, что длина гипотенузы равна $ d $.
Тогда длина противоположной стороны в точности равна половине длины гипотенузы.
$ Длина \, из \, Противоположная \, сторона $ $ \, = \, $ $ \ dfrac {Длина \, из \, Гипотенуза} {2} $
$ \ подразумевает $ Length \, of \, Opposite \, side $ $ \, = \, $ $ \ dfrac {d} {2} $
Длины противоположной стороны и гипотенузы известны. Их можно использовать для математического вычисления длины прилегающей стороны (основания) по теореме Пифагора.2}
долл. США
$ \ подразумевает OQ \, = \, \ dfrac {\ sqrt {3}} {2} d $
$ \ подразумевает OQ \, = \, \ dfrac {\ sqrt {3}} {2} \ times d $
$ \ подразумевает OQ \, = \, \ dfrac {\ sqrt {3}} {2} \ times OP $
$ \ следовательно \, \, Длина \, из \, Соседняя \, сторона \, = \, \ dfrac {\ sqrt {3}} {2} \ times Длина \, из \, Гипотенуза $
Проба
Свойства прямоугольного треугольника можно также доказать геометрически, построив примерный треугольник с углом в 30 градусов.
- Сначала проведите прямую горизонтальную линию от точки $ \ small R $.
- Используя транспортир, проведите прямую линию из точки $ \ small R $, но она должна составлять угол $ \ small 30 $ с горизонтальной линией.
- Возьмите компас и линейку, затем установите компас на $ \ small 10 \, \ normalsize cm $. После этого нарисуйте дугу на прямой $ \ small 30 $ градусов от точки $ \ small R $. Оба они пересекаются в точке $ \ small S $.
- Проведите перпендикулярную линию к горизонтальной линии из точки $ \ small S $, которая пересекает линию в точке $ \ small T $.° $.
Недвижимость
Длина прилегающей стороны (основания) равна $ \ dfrac {\ sqrt {3}} {2} $ раз длины гипотенузы, если угол равен $ 30 $ градусам.
Измерьте длину соседней стороны $ \ small \ overline {RT} $ линейкой и увидите, что длина соседней стороны равна $ 8.65 \, cm $. Позже вычислите длину соседней стороны теоретическим методом, чтобы сравнить разницу между ними.
$ Длина \, из \, Соседняя \, сторона $ $ \, = \, $ $ \ dfrac {\ sqrt {3}} {2} \ times Длина \, из \, Гипотенуза $
$ \ подразумевает $ Длина \, из \, Соседний \, сторона \, = \, \ dfrac {\ sqrt {3}} {2} \ times 10 $
$ \ подразумевает $ Length \, of \, прилегающие \, side \, = \, 8.{°} $.
.