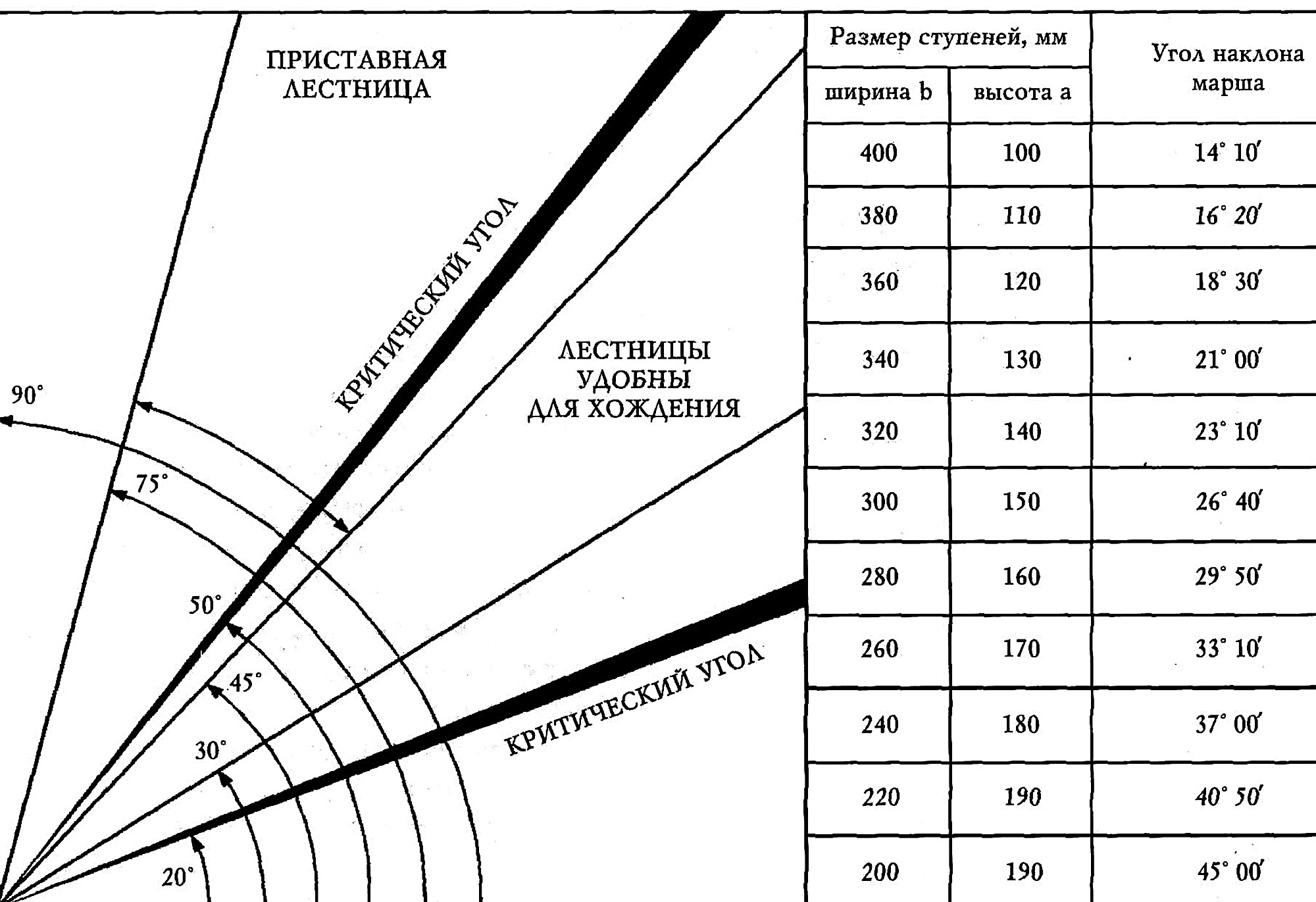
Таблица значений тригонометрических функций
Примечание. В данной таблице значений тригонометрических функций используется знак √ для обозначения квадратного корня. Для обозначения дроби — символ «/».
См. также полезные материалы:
- Формулы преобразования тригонометрических функций
- Таблица производных тригонометрических функций
- Как вычислены эти значения
Для определения значения тригонометрической функции, найдите его на пересечении строки с указанием тригонометрической функции. Например, синус 30 градусов — ищем колонку с заголовком sin (синус) и находим пересечение этой колонки таблицы со строкой «30 градусов», на их пересечении считываем результат — одна вторая. Аналогично находим косинус 60 градусов, синус 60 градусов (еще раз, в пересечении колонки sin (синус) и строки 60 градусов находим значение sin 60 = √3/2 ) и т. д. Точно так же находятся значения синусов, косинусов и тангенсов других «популярных» углов.
д. Точно так же находятся значения синусов, косинусов и тангенсов других «популярных» углов.
Приведенная ниже таблица косинусов, синусов и тангенсов также подходит для нахождения значения тригонометрических функций, аргумент которых задан в радианах. Для этого воспользуйтесь второй колонкой значений угла. Благодаря этому можно перевести значение популярных углов из градусов в радианы. Например, найдем угол 60 градусов в первой строке и под ним прочитаем его значение в радианах. 60 градусов равно π/3 радиан.
Число пи однозначно выражает зависимость длины окружности от градусной меры угла. Таким образом, пи радиан равны 180 градусам.
Любое число, выраженное через пи (радиан) можно легко перевести в градусную меру, заменив число пи (π) на 180.
Примеры:
1. Синус пи.
sin π = sin 180 = 0
таким образом, синус пи — это тоже самое, что синус 180 градусов и он равен нулю.
2. Косинус пи.
cos π = cos 180 = -1
таким образом, косинус пи — это тоже самое, что косинус 180 градусов и он равен минус единице.
3. Тангенс пи
tg π = tg 180 = 0
таким образом, тангенс пи — это тоже самое, что тангенс 180 градусов и он равен нулю.
Таблица значений синуса, косинуса, тангенса для углов 0 — 360 градусов (часто встречающиеся значения)
|
значение угла α (градусов) |
|
sin (синус) |
cos (косинус) |
tg (тангенс) |
ctg (котангенс) |
sec (секанс) |
cosec (косеканс) |
|
0 |
0 |
0 |
1 |
0 |
- |
1 |
- |
|
15 |
π/12 |
2 — √3 |
2 + √3 | ||||
|
30 |
π/6 |
1/2 |
√3/2 |
1/√3 |
√3 |
2/√3 |
2 |
|
45 |
π/4 |
√2/2 |
√2/2 |
1 |
1 |
√2 |
√2 |
|
60 |
π/3 |
√3/2 |
1/2 |
√3 |
1/√3 |
2 |
2/√3 |
|
75 |
5π/12 |
2 + √3 |
2 — √3 | ||||
|
90 |
π/2 |
1 |
0 |
- |
0 |
- |
1 |
|
105 |
7π/12 |
|
— |
— 2 — √3 |
√3 — 2 |
|
|
|
120 |
2π/3 |
√3/2 |
-1/2 |
-√3 |
-√3/3 | ||
|
135 |
3π/4 |
√2/2 |
-√2/2 |
-1 |
-1 |
-√2 |
√2 |
|
150 |
5π/6 |
1/2 |
-√3/2 |
-√3/3 |
-√3 | ||
|
180 |
π |
0 |
-1 |
0 |
- |
-1 |
- |
|
210 |
7π/6 |
-1/2 |
-√3/2 |
√3/3 |
√3 | ||
|
240 |
4π/3 |
-√3/2 |
-1/2 |
√3 |
√3/3 | ||
|
270 |
3π/2 |
-1 |
0 |
- |
0 |
- |
-1 |
|
360 |
2π |
0 |
1 |
0 |
- |
1 |
- |
Если в таблице значений тригонометрических функций вместо значения функции указан прочерк (тангенс (tg) 90 градусов, котангенс (ctg) 180 градусов) значит при данном значении градусной меры угла функция не имеет определенного значения. Если же прочерка нет — клетка пуста, значит мы еще не внесли нужное значение. Мы интересуемся, по каким запросам к нам приходят пользователи и дополняем таблицу новыми значениями, несмотря на то, что текущих данных о значениях косинусов, синусов и тангенсов самых часто встречающихся значений углов вполне достаточно для решения большинства задач.
Если же прочерка нет — клетка пуста, значит мы еще не внесли нужное значение. Мы интересуемся, по каким запросам к нам приходят пользователи и дополняем таблицу новыми значениями, несмотря на то, что текущих данных о значениях косинусов, синусов и тангенсов самых часто встречающихся значений углов вполне достаточно для решения большинства задач.
Таблица значений тригонометрических функций sin, cos, tg для наиболее популярных углов
0, 15, 30, 45, 60, 90 … 360 градусов
(цифровые значения «как по таблицам Брадиса»)
|
значение угла α (градусов) |
значение угла α в радианах |
sin (синус) |
cos (косинус) |
tg (тангенс) |
ctg (котангенс) |
|---|---|---|---|---|---|
|
0 |
0 |
|
|
|
|
|
15 |
|
|
|
|
|
|
30 |
|
|
|
|
|
|
45 |
|
|
|
|
|
|
|
|
|
|
|
|
|
60 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
75 |
|
|
|
|
|
|
90 |
|
|
|
|
|
|
|
|
|
|
|
|
|
120 |
|
|
|
|
|
|
135 |
|
|
|
|
|
|
|
|
|
|
|
|
|
150 |
|
|
|
|
|
|
180 |
|
|
|
|
|
|
270 |
|
|
|
|
|
|
360 |
|
|
|
|
|
Иногда для быстрых расчетов нужно не точное, а вычисляемое значение (число десятичной дробью), которое раньше искали в таблицах Брадиса. Поэтому, в дополнение к таблице точных значений тригонометрических функций приведены эти же самые значения, но в виде десятичной дроби, округленной до четвертого знака. Дополнительно в таблицу включены «нестандартные» значения тангенса, косинуса, синуса 140 градусов, синуса 105, 70, косинуса 105 и 50 градусов.
Поэтому, в дополнение к таблице точных значений тригонометрических функций приведены эти же самые значения, но в виде десятичной дроби, округленной до четвертого знака. Дополнительно в таблицу включены «нестандартные» значения тангенса, косинуса, синуса 140 градусов, синуса 105, 70, косинуса 105 и 50 градусов.
Пример: синус 60 градусов равен приблизительно 0,866025404, а в таблице указано значение sin 60 ≈ 0,8660 ; косинус 30 градусов равен этому же самому числу (см. формулы преобразования тригонометрических функций)
0
Начать курс обучения
Радиан, Углы больше 360 градусов, Положительные и отрицательные углы
Угол: °πrad =
Преобразовать в:
радианы0 — 360°положительноеотрицательное
Когда прямые пересекаются, то получается четыре разные области по отношению к точке пересечения.
Эти новые области называют углами.
На картинке видны 4 разных угла, образованных пересечением прямых AB и CD
Обычно углы измеряются в градусах, что обозначается как °.
Когда объект совершает полный круг, то есть движется из точки D через B, C, A, а затем обратно к D, то говорят что он повернулся на 360 градусов (360°).
Таким образом, градус — это $\frac{1}{360}$ круга.
Мы говорили о том, что когда объект делает полный круг вокруг точки, то он проходит 360°, однако, когда объект делает более одного круга, то он делает угол более 360 градусов. Это обычное явление в повседневной жизни. Колесо проходит многие круги, когда автомобиль движется, то есть оно образует угол больше 360°.
Для того, чтобы узнать количество циклов (пройденных кругов) при вращении объекта, мы считаем количество раз, которое нужно прибавить 360 к самому себе, чтобы получить число равное или меньшее, чем данный угол. Точно так же мы находим число, которое мы умножаем на 360, чтобы получить число меньшее, но наиболее близкое к данному углу.
Пример 2
1. Найти количество кругов, описанных объектом, образующем угол
a) 380°
b) 770°
c) 1000°
Решение
a) 380 = (1 × 360) + 20
Объект описал один круг и 20°
Так как $20^{\circ} = \frac{20}{360} = \frac{1}{18}$ круга
Объект описал $1\frac{1}{18}$ кругов. {\circ} = \frac{260}{360} = \frac{7}{9}$ кругов
{\circ} = \frac{260}{360} = \frac{7}{9}$ кругов
Объект описал $2\frac{7}{9}$ кругов
Когда объект вращается по часовой стрелки, то он образует отрицательный угол вращения, а когда вращается против часовой стрелке — положительный угол. До этого момента мы рассматривали только положительные углы.
В форме диаграммы отрицательный угол может быть изображен так, как это показано ниже.
Рисунок ниже показывает знак угла, который измеряется от общей прямой, 0 оси (оси абсцисс — х оси)
Это означает, что при наличии отрицательного угла, мы можем получить соответствующий ему положительный угол.
Например, нижняя часть вертикальной прямой это 270°. Когда измеряется в негативную сторону, то получим -90°. Мы просто вычитаем 270 из 360.
Имея отрицательный угол, мы прибавляем 360, для того чтобы получить соотвествующий положительный угол.
Когда угол равен -360°, это означает, что объект совершил более одного круга по часовой стрелке.
Пример 3
1. Найти соответствующий положительный угол
Найти соответствующий положительный угол
a) -35°
b) -60°
c) -180°
d) — 670°
2. Найти соответствующий отрицательный угол 80°, 167°, 330°и 1300°.
Решение
1. Для того, чтобы найти соответствующий положительный угол мы прибавляем 360 к значению угла.
a) -35°= 360 + (-35) = 360 — 35 = 325°
b) -60°= 360 + (-60) = 360 — 60 = 300°
c) -180°= 360 + (-180) = 360 — 180 = 180°
d) -670°= 360 + (-670) = -310
Это означает один круг по часовой стрелке (360)
360 + (-310) = 50°
Угол равен 360 + 50 = 410°
2. Для того, чтобы получить соответсвующий отрицательный угол мы вычитаем 360 от значения угла.
80° = 80 — 360 = — 280°
167° = 167 — 360 = -193°
330° = 330 — 360 = -30°
1300° = 1300 — 360 = 940 (пройден один круг)
940 — 360 = 580 (пройден второй круг)
580 — 360 = 220 (пройден третий круг)
220 — 360 = -140°
Угол равен -360 — 360 — 360 — 140 = -1220°
Таким образом 1300° = -1220°
Радиан — это угол из центра круга, в который заключена дуга, длина которой равна радиусу данного круга. {\circ}$
{\circ}$
c) 1 рад = 57,3°
$2,4 = \frac{2,4 \times 57,3}{1} = 137,52$
Отрицаетльные углы и углы больше, чем $2\pi$ радиан
Для того чтобы преобразовать отрицательный угол в положительный, мы складываем его с $2\pi$.
Для того чтобы преобразовать положительный угол в отрицательный, мы вычитаем из него $2\pi$.
Пример 5
1. Преобразовать $-\frac{3}{4}\pi$ и $-\frac{5}{7}\pi$ в позитивные углы в радианах.
Решение
Прибавляем к углу $2\pi$
$-\frac{3}{4}\pi = -\frac{3}{4}\pi + 2\pi = \frac{5}{4}\pi = 1\frac{1}{4}\pi$
$-\frac{5}{7}\pi = -\frac{5}{7}\pi + 2\pi = \frac{9}{7}\pi = 1\frac{2}{7}\pi$
Когда объект вращается на угол больший, чем $2\pi$;, то он делает больше одного круга.
Для того, чтобы определить количество оборотов (кругов или циклов) в таком угле, мы находим такое число, умножая которое на $2\pi$, результат равен или меньше, но как можно ближе к данному числу.
Пример 6
1. Найти количество кругов пройденных объектом при данных углах
Найти количество кругов пройденных объектом при данных углах
a) $-10\pi$
b) $9\pi$
c) $\frac{7}{2}\pi$
Решение
a) $-10\pi = 5(-2\pi)$;
$-2\pi$ подразумевает один цикл в направлении по часовой стрелке, то это означает, что
объект сделал 5 циклов по часовой стрелке.
b) $9\pi = 4(2\pi) + \pi$, $\pi =$ пол цикла
объект сделал четыре с половиной цикла против часовой стрелки
c) $\frac{7}{2}\pi=3,5\pi=2\pi+1,5\pi$, $1,5\pi$ равно три четверти цикла $(\frac{1,5\pi}{2\pi}=\frac{3}{4})$
объект прошел один и три четверти цикла против часовой стрелки
Угол 60 градусов — Значение, конструкция, примеры
Угол 60 градусов является острым углом, так как углы меньше прямого угла (менее 90°) называются острыми углами. В случае геометрического угла дуга центрируется в вершине и ограничивается сторонами. В случае вращения дуга центрируется в центре вращения и ограничивается любой другой точкой и ее изображением при вращении. Давайте узнаем больше об углах 60 градусов, способах их построения и решим несколько примеров, чтобы лучше понять концепцию.
Давайте узнаем больше об углах 60 градусов, способах их построения и решим несколько примеров, чтобы лучше понять концепцию.
| 1. | Что такое угол 60 градусов? |
| 2. | Значение угла 60 градусов |
| 3. | Построение угла 60 градусов |
| 4. | Углы 60 градусов в реальной жизни |
| 5. | Часто задаваемые вопросы об угле 60 градусов |
Что такое угол 60 градусов?
Угол 60 градусов является острым углом в геометрии и выражается как π/3 в радианах. Каждый угол равностороннего треугольника равен 60 градусам. Мы можем построить угол 60 градусов с помощью циркуля, транспортира и линейки и наблюдать этот угол в нашей повседневной жизни на различных объектах.
Значение угла 60 градусов
Мы знаем, что угол образуется, когда два луча встречаются в вершине. Если угол, образованный при вершине О, равен 60 градусам, мы называем его углом 60 градусов. Размер каждого угла равностороннего треугольника равен 60°. Поэтому его также называют треугольником с углом 60 градусов. Углы также могут быть представлены в радианах, т.е. пи (π) и пи (π) радиан = 180°. Следовательно, 60° можно выразить в радианах как π/3 радиан.
Если угол, образованный при вершине О, равен 60 градусам, мы называем его углом 60 градусов. Размер каждого угла равностороннего треугольника равен 60°. Поэтому его также называют треугольником с углом 60 градусов. Углы также могут быть представлены в радианах, т.е. пи (π) и пи (π) радиан = 180°. Следовательно, 60° можно выразить в радианах как π/3 радиан.
Построение угла 60 градусов
Построение угла 60 градусов является одним из самых основных построений, так как он формируется как строительный угол и для других измерений. Давайте рассмотрим, как построить угол 60 градусов с помощью транспортира. Выполните указанные шаги:
- Шаг 1: Нарисуйте отрезок OA
- Шаг 2: Поместите транспортир в точку O
- Шаг 3: Во внешнем круге транспортира найдите показание 60 градусов, карандашом отметьте точку и назовите ее C
- Шаг 4: Соедините O и C. Теперь ∠AOC=60°
Углы 60 градусов в реальной жизни
Углы окружают нас повсюду. Например, когда мы открываем рот, наши губы образуют угол. Когда минутная стрелка часов находится на 12, а часовая на 2, угол, образованный между двумя стрелками, составляет 60°. Некоторые дорожные знаки имеют форму равностороннего треугольника, а мера каждого угла равностороннего треугольника составляет 60°. Угол 60 градусов используется в архитектуре для создания дизайнерских домов, дверей и оконных решеток.
Например, когда мы открываем рот, наши губы образуют угол. Когда минутная стрелка часов находится на 12, а часовая на 2, угол, образованный между двумя стрелками, составляет 60°. Некоторые дорожные знаки имеют форму равностороннего треугольника, а мера каждого угла равностороннего треугольника составляет 60°. Угол 60 градусов используется в архитектуре для создания дизайнерских домов, дверей и оконных решеток.
На изображении ниже показаны различные примеры ракурсов в нашем окружении. Обратите внимание, где вы можете видеть углы в 60 градусов в окружающих вас областях.
Важные замечания по углу 60 градусов
- Угол 60 градусов в геометрии является острым углом.
- Равносторонний треугольник называется треугольником с углом 60 градусов, так как мера каждого угла в нем равна 60 градусам.
- Мы можем построить угол 60 градусов, используя транспортир, циркуль и линейку.
Похожие статьи
- Угол 30 градусов
- Прямоугольный
- Угол 180 градусов
- Треугольники
Решенные примеры для угла 60 градусов
Пример 1: В ΔABC используйте транспортир для измерения ∠CAB.

Решение: Поместите базовую линию транспортира вдоль линии AB и центр транспортира в вершине A. Обратите внимание на показания транспортира, которые перекрываются с линией AC.
Ответ: Следовательно, ∠CAB = 60°
Пример 2: Помогите Джози построить угол 60°.
Решение: Вот шаги, которые Джози может выполнить, чтобы построить угол 60°
Шаг-1: Нарисуйте линию OP.
Шаг 2:
- Поместите транспортир на линию OP.
- Поместите середину транспортира в точку O.
Шаг-3:
- На OP справа, начните отсчет с 0° в порядке возрастания, отметьте точку Q с помощью острого карандаша в точке, показывающей 60°.
- Снимите транспортир и присоединитесь к OQ.
- Получаем искомый угол ∠QOP = 60°.
Ответ: Следовательно, ∠QOP = 60°
перейти к слайдуперейти к слайду
Как ваш ребенок может освоить математические понятия?
Мастерство математики приходит с практикой и пониманием «почему» за «что». Почувствуйте разницу с Cuemath.
Почувствуйте разницу с Cuemath.
Записаться на бесплатный пробный урок
Практические вопросы по углу 60 градусов
перейти к слайдуперейти к слайдуперейти к слайду
Часто задаваемые вопросы об угле 60 градусов
Что такое угол 60 градусов?
Угол 60 градусов является острым, потому что он меньше 90 градусов. 60° в радианах равно π/3, а мера каждого угла равностороннего треугольника равна 60°. Поэтому его также называют треугольником с углом 60 градусов.
Как построить угол 60 градусов с помощью транспортира?
Чтобы построить угол в 60 градусов, необходимо 2 дуги, чтобы нарисовать угол в 60 градусов. Вот шаги для построения угла в 60 градусов:
Шаг 1: Нарисуйте отрезок PQ
Шаг 2: Поместите транспортир в точку P
.
Шаг 3: Во внешнем круге транспортира найдите показание 60°, отметьте карандашом точку и назовите ее R
.
Шаг 4: Соедините P и R. Теперь ∠QPR=60°
Что вы называете углом в 60 градусов?
Угол, градусная мера которого больше 0°, но меньше 90°, называется острым углом. Углы 30°, 40°, 60° являются острыми углами. Поэтому угол в 60 градусов называется острым углом.
Углы 30°, 40°, 60° являются острыми углами. Поэтому угол в 60 градусов называется острым углом.
Как найти угол 60 градусов без транспортира?
Вот шаги, необходимые для построения угла 60 градусов без транспортира:
Шаг 1: Нарисуйте отрезок (AB). Установив компас в точку A, проведите дугу через точку AB и вверх над указанной выше точкой A.
Шаг 2: Не меняя ширины компаса, переместите компас в точку, где дуга пересекает АВ, и нарисуйте дугу, пересекающую первую.
Шаг 3: Соедините точку A с точкой пересечения двух дуг (точка C). ∠CAB = 60°
Сколько углов в 60 градусов нужно, чтобы сделать полный оборот?
Углы измеряются в градусах, и в одном полном обороте, который завершает один полный круг, содержится 360 градусов. Так как 60 × 6 = 360, то на один полный оборот приходится шесть углов по 60°.
Что такое угол 60 градусов в радианах?
Мы можем выразить угол 60 градусов в радианах, используя формулу: Угол в радианах = Угол в градусах × π/180. Итак, у нас есть 60 градусов в радианах = 60 × π/180 = π/3 радиан.
Итак, у нас есть 60 градусов в радианах = 60 × π/180 = π/3 радиан.
Скачать БЕСПЛАТНЫЕ учебные материалы
Угловые рабочие листы
Построение угла 60 градусов
30-DAY PROMIS | ПОЛУЧИТЕ 100% ВОЗВРАТ ДЕНЕГ*
*T&C Apply
LearnPracticeDownload
В геометрии построение — это процесс рисования фигуры, формы или множества различных типов углов. Мы рисуем такие фигуры с помощью геометрических инструментов, таких как циркуль, транспортир, линейка. При построении углов мы используем циркуль для рисования дуг и линейку для рисования отрезков и измерения их длины. Мы можем нарисовать угол в 60 градусов, используя любой из двух геометрических инструментов, транспортир или циркуль. В этом мини-уроке мы подробно научимся строить угол 60 градусов с помощью транспортира и циркуля.
| 1. | Построение угла 60 градусов с помощью транспортира |
2. | Построение угла 60 градусов с помощью компаса |
| 3. | Решенные примеры построения угла 60 градусов |
| 4. | Практические вопросы по построению угла 60 градусов |
| 5. | Часто задаваемые вопросы о построении угла 60 градусов |
Построение угла 60 градусов с помощью транспортира
Построение углов с помощью транспортира — очень простой метод. Транспортир — это геометрический инструмент, который можно использовать как для измерения, так и для рисования углов. Давайте рассмотрим шаги, которые рассказывают нам о построении угла в 60 градусов с помощью транспортира.
Прочитайте приведенные шаги и попробуйте сами.
- Шаг 1. С помощью линейки и карандаша нарисуйте отрезок AB.
- Шаг 2. Теперь отметьте центр сегмента линии как O.
- Шаг 3. Возьмите транспортир и поместите его в точку 0.
- Шаг 4. Теперь найдите угол 60 градусов в транспортире (во внешней окружности транспортира), отметьте точку и назовите ее C.

- Шаг 5. Теперь соедините точки O и C.
- Шаг 6: После соединения линий получим ∠AOC = 60°.
Посмотрите на данное изображение построения угла 60 градусов с помощью транспортира.
Примечание. Угол 60 градусов является острым углом, т.е. меньше 90 градусов.
Построение угла 60 градусов с помощью компаса
Построение углов с помощью циркуля несколько сложнее, чем построение с помощью транспортира. Циркуль — это геометрический инструмент, используемый для рисования дуг и окружностей. Давайте рассмотрим шаги, которые рассказывают нам о построении угла в 60 градусов с помощью циркуля.
Предположим, что у вас есть прямая L и некоторая точка A на L, как показано на рисунке.
Теперь давайте попробуем построить луч (или линию) через точку A, наклоненную под углом 60° к L. и нарисуйте дугу любой длины радиуса, которая пересекает L в точке B , как показано на рисунке ниже.
- Шаг 2: Теперь, взяв B за центр и AB за радиус, нарисуйте еще одну дугу, которая пересекает первую дугу в точке C:
- Шаг 3: Проведите луч (или линию) через точки A и C. Он будет наклонен под углом 60° к L :
Здесь AB = AC, так как это радиусы одной и той же дуги окружности. Кроме того, BC = BA, так как это тоже радиусы одной и той же (второй) дуги окружности. Таким образом, АВ = ВС = АС. Это означает, что треугольник ABC равносторонний, поэтому угол BAC = 60°.
Обратите внимание, что, разделив пополам угол 60°, мы можем построить угол 30°, а разделив пополам угол 30°, мы можем построить угол 15°.
Связанные статьи о построении угла в 60 градусов
Ознакомьтесь с интересными статьями по ссылкам ниже, чтобы узнать больше о терминологии, связанной с построением угла в 60 градусов.
- Сущность геометрических построений
- Построение биссектрисы угла
- Построение биссектрисы перпендикуляра
- Построение угла 90 градусов
- Построение перпендикуляра от точки к линии
- Транспортир
- Острые углы
Пример 1: Постройте угол 60 градусов с помощью циркуля и разделите его пополам.
Решение: Чтобы построить угол 60 градусов с помощью компаса, нам нужно выполнить следующие шаги.
- Шаг 1: Нарисуйте отрезок PQ любого измерения.
- Шаг 2: С помощью компаса постройте ∠GPQ = 60°. Из точки P проведите дугу на PQ. Назовите его E. Теперь, взяв E за центр и PE за радиус, нарисуйте еще одну дугу, пересекающую первую дугу в точке F. Проведите луч (или линию) через точки P и F, наклоненный под углом 60°.
- Шаг 3: Разделите ∠GPQ пополам с помощью компаса, возьмите любой радиус, который пересекает линии PQ и PG в точках E и F.

- Шаг 4: Теперь с помощью компаса возьмем радиус больше EF и проведем по одной дуге из точек E и F соответственно.
- Шаг 5: Пересечение обех дуг в точке L показано на изображении. Продолжайте движение по PL в направлении J.
- Шаг 6: Полученный угол ∠JPQ является биссектрисой ∠GPQ.
.
∠GPQ = 60° и ∠JPQ = 30°.
Пример 2. Сколько углов по 60 градусов содержит прямой угол?
Решение: Мы это знаем,
Измерение полного угла = 360°.
Измерение прямого угла = 180°.
Теперь, чтобы найти количество углов в 60 градусов в прямом угле, мы разделим 180 градусов на 60 градусов.
180 ÷ 60 = 3,
Таким образом, в прямом угле всего три угла по 60 градусов.
перейти к слайдуперейти к слайду
Есть вопросы по основным математическим понятиям?
Станьте чемпионом по решению проблем, используя логику, а не правила. Узнайте, почему стоит математика, с сертифицированными экспертами ourCuemath.
Узнайте, почему стоит математика, с сертифицированными экспертами ourCuemath.
Записаться на бесплатный пробный урок
перейти к слайдуперейти к слайдуперейти к слайду
Часто задаваемые вопросы о построении угла 60 градусов
Как построить угол 60 градусов?
Мы можем построить угол в 60 градусов, используя два геометрических инструмента – транспортир и циркуль. Давайте сначала рассмотрим процедуру, которую нам нужно выполнить при построении угла в 60 градусов с помощью транспортира. С помощью линейки и карандаша начертите отрезок. Теперь отметьте центр на отрезке линии. Возьмите транспортир и поместите его в центральную точку. Теперь найдите на транспортире угол 60 градусов, отметьте точку и назовите ее. Теперь соедините отмеченную точку и центральную точку прямой линией. После присоединения к линии угол будет равен 60°.
Как построить угол в 60 градусов без транспортира?
С помощью циркуля мы можем нарисовать угол 60 градусов без транспортира. Рассмотрим процедуру построения угла 60 градусов с помощью циркуля. Нарисуйте любую линию А и отметьте на ней точку О. Взяв О за центр, поместите стрелку компаса в точку О и начертите полную полудугу любого радиуса, которая пересекает линию А в некоторой точке. Назовите точку B. Теперь, взяв B за центр и OB за радиус, нарисуйте еще одну дугу, пересекающую первую дугу. Дайте имя точке, которая является точкой пересечения двух дуг. Допустим, C. Проведите луч (или линию) через O и C. Он будет наклонен под углом 60° к линии A.
Рассмотрим процедуру построения угла 60 градусов с помощью циркуля. Нарисуйте любую линию А и отметьте на ней точку О. Взяв О за центр, поместите стрелку компаса в точку О и начертите полную полудугу любого радиуса, которая пересекает линию А в некоторой точке. Назовите точку B. Теперь, взяв B за центр и OB за радиус, нарисуйте еще одну дугу, пересекающую первую дугу. Дайте имя точке, которая является точкой пересечения двух дуг. Допустим, C. Проведите луч (или линию) через O и C. Он будет наклонен под углом 60° к линии A.
Как построить угол 60 градусов в начальной точке данного луча?
С помощью транспортира можно построить угол 60 градусов в начальной точке данного луча. Найдите угол 60 градусов во внешнем круге (если отрезок направлен влево) или во внутреннем круге (если отрезок направлен вправо) транспортира, поместив транспортир в заданную точку. точка. Отметьте точку и подпишите ее. Теперь соедините точки. После соединения линий угол будет равен 60°. Обратите внимание, что угол 60 градусов всегда является острым углом.
Как разделить пополам угол 60 градусов?
Построив половину угла в 60 градусов, т.е. построив угол в 30 градусов, мы можем разделить пополам угол в 60 градусов. Это возможно с помощью компаса. Посмотрите на приведенные ниже шаги, чтобы разделить пополам угол в 60 градусов с помощью компаса:
- Шаг 1: Начертите отрезок любой длины и назовите его. Допустим, МН
- Шаг 2: С помощью циркуля постройте угол = 60°.
- Шаг 3: Из точки M проведите дугу на MN. Назовите его Q. Теперь, приняв Q за центр и MQ за радиус, нарисуйте еще одну дугу, которая пересекает первую дугу в точке F. Проведите луч (или линию) через M и соедините MF, наклоненную под углом 60°. Продлите линию до некоторой точки и назовите ее G.
- Шаг 4: Разделите ∠GMN пополам с помощью компаса, возьмите любой радиус, который пересекает линии MN и MG в точках Q и F.
- Шаг 5: Теперь с помощью компаса возьмем радиус больше QF и проведем по одной дуге из точек Q и F соответственно.

.
.

 1918
1918