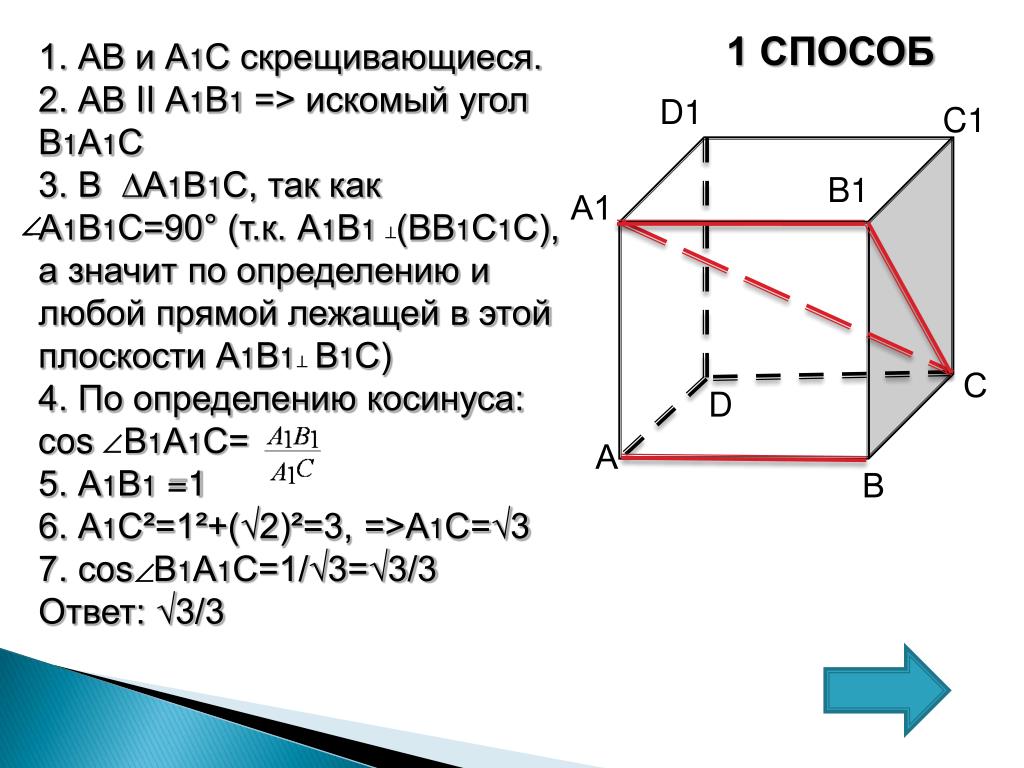
Искомый угол это: Чему равен искомый угол? — Две параллельные прямые живут в эвклидовом мирке и бегают пересекаться в мир лобачевского тайком. — LiveJournal — Информационный портал города Мичуринска. Афиша

Содержание

Углы — Стереометрия — Подготовка к ЕГЭ по математике

Углы

Классическим заданием с развернутым ответом на стереометрию является задача на нахождение угла. В стереометрии найти угол могут предложить между следующими комбинациями фигур:

Рассмотрим каждую комбинацию, чтобы понять, как искать разные виды углов и какие методы можно применять.

УГОЛ МЕЖДУ СКРЕЩИВАЮЩИМИСЯ ПРЯМЫМИ

Угол между скрещивающимися прямыми ? это угол между параллельными им прямыми, лежащими в одной плоскости.

Это значит, что никогда не пересекающиеся прямые в пространстве мы делаем «пересекающимися»: для этого нужно построить пересекающиеся прямые, параллельные данным. Угол между ними будет искомым.

Часто достаточно только к одной из скрещивающихся прямых построить параллельную прямую.

Например, если бы мы отметили точку M на прямой b и через точку M провели прямую

УГОЛ МЕЖДУ ПРЯМОЙ И ПЛОСКОСТЬЮ

Угол между прямой и плоскостью — угол между прямой и ее проекцией на эту плоскость.

Для того, чтобы найти угол между прямой и плоскостью, нужно сначала получить проекцию этой прямой на плоскость, а потом найти угол.

Прямая, пересекающая плоскость ? в точке O

Из произвольной точки А на прямой опустим перпендикуляр AH на плоскость ?.

Тогда OH – проекция прямой на плоскость ?.

Угол между прямой и наклонной, то есть ? AOH и есть искомый угол между .

УГОЛ МЕЖДУ ПЛОСКОСТЯМИ

Для начала вспомним пару определений:

Метод перпендикуляров к линии пересечения.Нахождения угла между плоскостями – одна из самых сложных задач на углы, поэтому тут мы можем воспользоваться несколькими методами.

Угол между плоскостями вычисляется как угол между прямыми, лежащими в этих плоскостях и перпендикулярными к линии их пересечения. Это основной способ нахождения угла между плоскостями.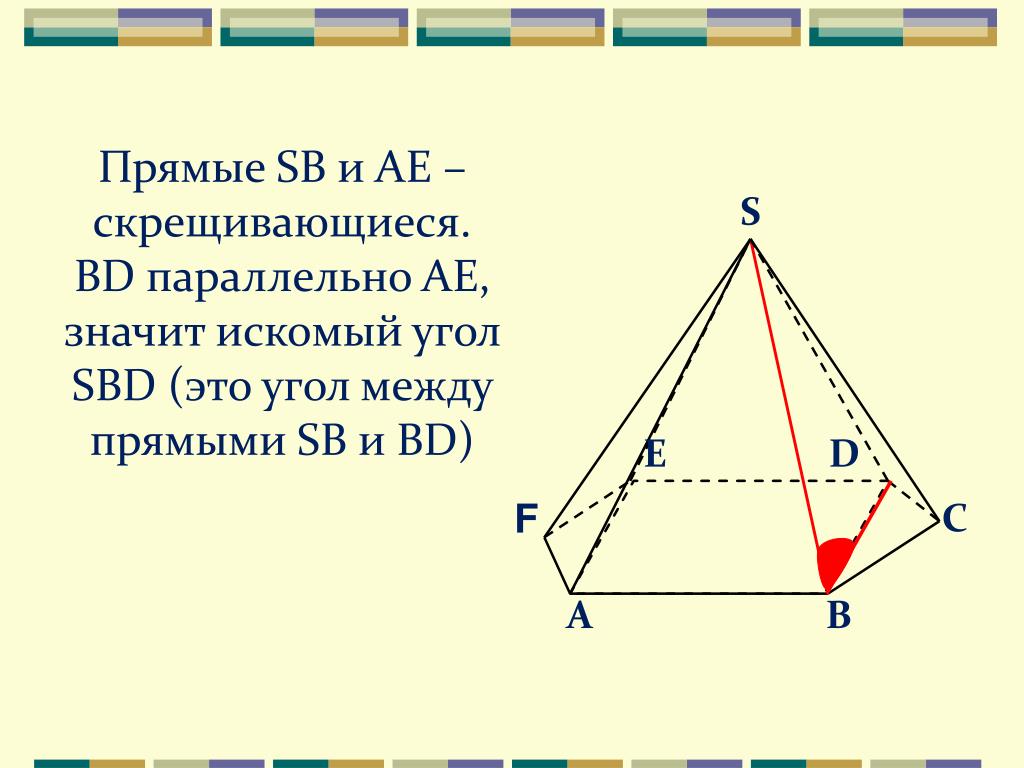

Находим линию пересечения плоскостей ? и ? – AB.

Из «удобной» точки К в плоскости ? (это может быть вершина многогранника, середина ребра и т.д.) опускаем перпендикуляр KH на AB.

В точку H опустим перпендикуляр из точки M в плоскости ?.

? KHM – искомый угол между плоскостями ? и ?

Метод перпендикуляров к плоскостям.

Угол между плоскостями вычисляется как угол между перпендикулярами к данным плоскостям. Этот способ удобен, если перпендикуляр к плоскости построить удобнее, чем построить перпендикуляры к линии пересечения плоскостей (или перпендикуляр к плоскости уже есть по условию задачи).

Из произвольной точки O пространства опустим перпендикуляр OM на плоскость ?.

Из точки O опустим так же перпендикуляр OH на плоскость ?.

Любой из двух смежных углов между OM и OH может считать искомым, но так как угол между плоскостями измеряется от 0 до 90°, то берем острый.

? MOK – искомый угол между плоскостями ? и ?

Метод параллельных плоскостей.

Угол между плоскостями вычисляется как угол между плоскостями, параллельными данным плоскостям. Этот способ применим, когда угол между данными плоскостями по каким-то причинам искать неудобно, а удобнее найти угол между плоскостями, параллельными данным.

Угол между плоскостями ? и ? затруднительно искать (например, нет «удобных точек» или тяжело построить взаимные перпендикуляры).

Построим плоскость ?, параллельную ? (или в стереометрической фигуре она уже есть)

По методу перпендикуляров к линии пересечения найдем угол между плоскостями ? и ?.

? MНK – искомый угол между плоскостями ? и ?

Чему равен искомый угол? | Yablor.ru

Yablor.ru — рейтинг блогов рунета, автоматически упорядоченных по количеству посетителей, ссылок и комментариев.

Фототоп — альтернативное представление топа постов, ранжированных по количеству изображений. Видеотоп содержит все видеоролики, найденные в актуальных на данных момент записях блогеров. Топ недели и топ месяца представляют собой рейтинг наиболее популярных постов блогосферы за указанный период.

В разделе рейтинг находится статистика по всем блогерам и сообществам, попадавшим в основной топ. Рейтинг блогеров считается исходя из количества постов, вышедших в топ, времени нахождения поста в топе и занимаемой им позиции.

gera544 — 01.10.2020

Точки А, В и С лежат на одной прямой. Квадраты равны. Найти угол
отмеченный знаком вопроса.

Сохранено

Источник

Оставить комментарий

тригонометрия — Найдите нужный угол

Если стеллаж с полками почти вертикальный и вам не нужна большая точность, чтобы навести камеру на нужную полку, то вы можете получить хороший результат с помощью простой триангуляции.

Пусть положительные углы наклона представляют собой наведение камеры над горизонталью, и пусть $h$ — известное расстояние по вертикали между верхней и нижней целевыми точками QR-кода, а $d$ — расстояние по горизонтали от камеры до поверхности полки. Ссылаясь на приведенную выше иллюстрацию, мы имеем $$h={d\over\tan\alpha}+{d\over\tan\beta}$$, что при решении для $d$ дает $$d={\sin\alpha \sin\beta\over\sin(\alpha+\beta)}h.$$ Подставляя $\alpha=\frac\pi2-\theta_{\text{top}}$ и $\beta=\frac\pi2+\theta_ {\text{bot}}$ и упрощая, мы получаем $$d={\cos\theta_{\text{top}}\cos\theta_{\text{bot}}\over\sin(\theta_{ \text{top}}-\theta_{\text{bot}})}h. $$ Таким образом, угол наклона $0$ соответствует точке на расстоянии $d\tan\theta_{\text{top}} $ ниже верхней цели (выше, если это значение отрицательное, конечно), поэтому угол наклона точки на расстоянии $y\ge0$ ниже вершины удовлетворяет $$\tan\theta={d\tan\theta_{ \text{top}}-y\over d}=\tan\theta_{\text{top}}-\frac yd.$$ Я оставлю вам вычислить соответствующие формулы для расстояний, измеренных от дна цель вместо этого. Остерегайтесь ошибок в знаках!

Если вам нужна более высокая точность, чем эта, или полки не почти перпендикулярны линии нулевого наклона камеры, тогда вам нужно сделать что-то более сложное, например, расчет, описанный в ответе Орена, или, возможно, с использованием гомографии между изображением с камеры и плоскостью поверхности полки (что в данном случае несложно вычислить). Потенциальное преимущество последнего заключается в том, что после вычисления матрицы преобразования вы можете найти луч в мировых координатах от камеры до любой точки на поверхности полки. 2)\over2(c_{out}-c_{in})}.\tag1$$ У нас также есть $$r_{out}={h\over2\sin\Delta\theta_{out}}, c_{out }=r_{out}\cos\Delta\theta_{out} \\ r_{in}={h-2q\over2\sin\Delta\theta_{in}}, c_{in}=r_{in}\cos \Delta\theta_{in}.$$ Подставляя эти значения в (1) и упрощая, получаем $$x={q(h-q)\over h\cot\Delta\theta_{out}-(h-2q)\cot \Delta\theta_{in}}.\tag2$$ Абсолютное значение $x$ — это перпендикулярное расстояние $d$ до поверхности полки. Отсюда вы можете вычислить $y$-координаты пересечений, выбрать ту, которая соответствует вашей ситуации, и использовать эту точку для вычисления смещения угла наклона $\delta$ (который также является углом, на который полки отклоняются от перпендикуляра к линии нулевого наклона). Затем вы можете продолжить, как и раньше, изменив полученные углы наклона на $\delta$. Это вычисление также может быть необходимо, если камера не выровнена, т. е. нулевой наклон значительно отклоняется от горизонтали.

комбинаторика — какое минимальное количество линий гарантирует наличие хотя бы одного угла меньше 26 градусов (Применение принципа сортировки)

$\begingroup$

Вопрос : На плоскости есть n непараллельных прямых. Эти линии будут образовывать несколько углов (рис. Q11 а). Каково минимальное количество линий, чтобы хотя бы один угол был меньше 26 градусов? Почему? (Совет: перевод прямой линии не меняет угол, показанный на рис. Q11 б)

Решение : требуется 7 строк. Причина:

Так как перевод прямой линии не меняет угол,
мы можем переместить эти прямые и позволить им иметь только одну точку пересечения.
Следовательно, n прямых образуют 2n углов. Чтобы хотя бы один угол был меньше 26 градусов, нам нужно $\lceil \frac{360}{26}\rceil +1=14$. Следовательно, нужно 14 углов, а нам нужно 7 линий.

Хотя я прочитал решение, меня смущают две вещи.

Учитывая тот факт, что длина линии бесконечна и они непараллельны, эти прямые будут иметь два или более пересечений с другими линиями, когда есть три линии или более. Поэтому мне не понятно такое объяснение «Поскольку перевод прямой не меняет угол, мы можем сдвинуть эти прямые и пусть у них будет только одна точка пересечения». \circ$.
Формула, использованная в решении: $\lceil\frac{360}{26}\rceil+1$ на самом деле дает неправильный результат $15$ вместо $14$ (из-за добавления $1$). Правильная формула получается из решения $26x>360$ для целого числа $x$ (количество углов). Это сводится к $x>\frac{360}{26}$, что снова сводится к $x>\lfloor\frac{360}{26}\rfloor$ (поскольку $x$ — количество углов — равно целое число), что совпадает с $x\ge\lfloor\frac{360}{26}\rfloor+1$ (поскольку целое число больше другого целого числа $n$ тогда и только тогда, когда оно не менее $n +1$).
$\endgroup$
$\begingroup$
Слишком много, чтобы уместиться в комментарии, так что мы здесь.
Я не согласен с тем, что мы не можем применить принцип сортировки; голуби — это градусы, а голуби — по одному градусу — вы собираете их в кучу. Вы пускаете голубей в дырки по $26$ за раз, выпуская $13$ пучков $13\cdot26=338$. В следующей связке голубей не будет достаточно дырок, поэтому появится $+1$. Если бы вы использовали большие пучки, в последнем пучке было бы еще меньше отверстий (меньший угол). Меньшие грозди уже были бы ниже 26$ градусов. Итак, нам нужно 14$ пучков — 14$ уголков.
В первой части давайте рассмотрим все в обратном порядке. Представьте себе три прямые, которые пересекаются в одной точке. Два перпендикулярны, вертикальны и горизонтальны. Третий пересекается на их пересечении под углом $35$ градусов. Теперь у вас есть шесть углов, по два по 90, 55 и 35 градусов каждый.
Теперь переместите наклонную линию вверх, не изменяя ее наклон. Одно пересечение превращается в три пересечения и $12$ углов, но обратите внимание, что все углы имеют ту же меру, что и раньше. У нас есть четыре $9Углы 0$ градусов, четыре угла 55$ градусов и четыре угла 35$ градусов.
Другими словами, перевод линии — перемещение ее без изменения угла — сохранил все углы. И это будет верно для любого количества строк. Таким образом, где бы ни начинались наши непараллельные линии, мы можем преобразовать их в пересечения в одной точке, и меры углов не изменятся.

Искомый угол это: Чему равен искомый угол? — Две параллельные прямые живут в эвклидовом мирке и бегают пересекаться в мир лобачевского тайком. — LiveJournal

Углы — Стереометрия — Подготовка к ЕГЭ по математике

Чему равен искомый угол? | Yablor.ru

Оставить комментарий

Популярные посты:

тригонометрия — Найдите нужный угол

комбинаторика — какое минимальное количество линий гарантирует наличие хотя бы одного угла меньше 26 градусов (Применение принципа сортировки)

Добавить комментарий Отменить ответ