Как найти 90 градусов без угольника: Как построить прямой угол на земле при помощи простейших инструментов?

Линейки, рейсшины для черчения, транспортиры, угольники, трафареты и лекала

• Показать все

Похожие товары

Сортировать по

цене

↓
↑

популярности

↓
↑

×

Линейка офицерская, гибкая, прозрачная. Необходима при создании графических изображений и построении карт. Содержит 65 специальных элемента и линейку 20 см с отливной
шкалой.

001221

Линейка 20см офицерская, арт.СТ-ТТ-02

29.16 р.

Купить

+ 1 шт

+ 5 шт

+ 10 шт

шт.
×
29. 16
р.

Итого:
29.16
р.

В корзину

Показать отфильтрованные товары ()

Дополнительные товары

цена от 29.16 р.

001221

Линейка 20см офицерская, арт.СТ-ТТ-02

29.16 р.

Купить

+ 1 шт

+ 5 шт

+ 10 шт

шт.
×
29.16
р.

Итого:
29.16
р.

В корзину

×

30-сантиметровая линейка Attache выполнена из полистирола. Линейка удобна в использовании, четкая разметка и высокое качество. Флуоресцентные цвета: желтый, малиновый,
оранжевый, зеленый.

020935

Линейка 30см, пластмассовая, флюоресц., цвета в ассорт, Attache, ст.20

38.03 р.

Купить

+ 1 шт

+ 5 шт

+ 10 шт

шт.
×
38.03
р.

Итого:
38.03
р.

В корзину

Показать отфильтрованные товары ()

Дополнительные товары

цена от 38.03 р.

020935

Линейка 30см, пластмассовая, флюоресц., цвета в ассорт, Attache, ст.20

38.03 р.

Купить

+ 1 шт

+ 5 шт

+ 10 шт

шт.
×
38.03
р.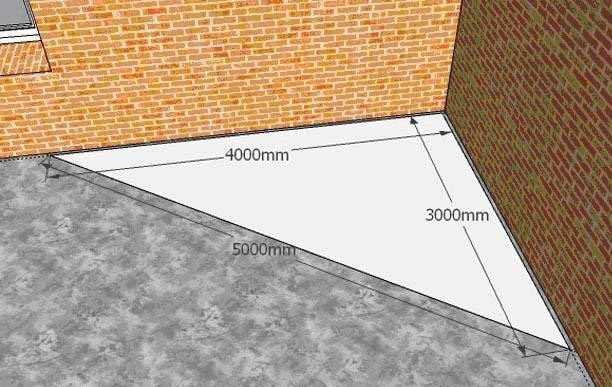

Итого:
38.03
р.

В корзину

Линейка выполнена из сертифицированного полистирола с гладкой глянцевой поверхностью. Предназначена для чертежных работ. На линейку нанесена ровная, четкая миллиметровая
шкала. Линейка имеет безопасные закруглённые углы.

005431

Линейка 30см, пластмассовая, черная, Стамм арт.ст-лн-35, ст.20

35.74 р.

Купить

+ 1 шт

+ 5 шт

+ 10 шт

шт.
×
35.74
р.

Итого:
35.74
р.

В корзину

Показать отфильтрованные товары ()

Дополнительные товары

цена от 35.74 р.

005431

Линейка 30см, пластмассовая, черная, Стамм арт. ст-лн-35, ст.20

35.74 р.

Купить

+ 1 шт

+ 5 шт

+ 10 шт

шт.
×
35.74
р.

Итого:
35.74
р.

В корзину

×

Линейка яркого флуоресцентного цвета с гладкой глянцевой поверхностью. Предназначена для чертежных работ. Имеет безопасные закругленные углы. Изготовлена из сертифицированного
полистирола.

013872

Линейка 20см, пластмассовая, флюоресц., Стамм, ЛФ20, ст.1

26.99 р.

Купить

+ 1 шт

+ 5 шт

+ 10 шт

шт.
×
26. 99
р.

Итого:
26.99
р.

В корзину

Показать отфильтрованные товары ()

Дополнительные товары

цена от 26.99 р.

013872

Линейка 20см, пластмассовая, флюоресц., Стамм, ЛФ20, ст.1

26.99 р.

Купить

+ 1 шт

+ 5 шт

+ 10 шт

шт.
×
26.99
р.

Итого:
26.99
р.

В корзину

30-сантиметровая линейка Attache выполнена из стали. Линейка применяется для чертежных и измерительных работ и имеет двойную градацию шкалы (сантиметр, дюйм). Ширина линейки
25 мм. Толщина стали — 0,8 мм.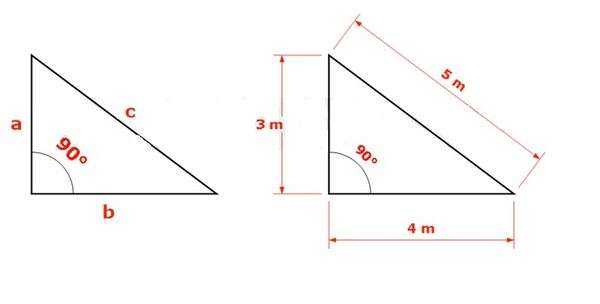

005873

Линейка 30см, металлическая, Attache, ст.10

88.31 р.

Купить

+ 1 шт

+ 5 шт

+ 10 шт

шт.
×
88.31
р.

Итого:
88.31
р.

В корзину

Показать отфильтрованные товары ()

Дополнительные товары

цена от 88.31 р.

005873

Линейка 30см, металлическая, Attache, ст.10

88.31 р.

Купить

+ 1 шт

+ 5 шт

+ 10 шт

шт.
×
88.31
р.

Итого:
88. 31
р.

В корзину

×

Пластиковая линейка с закругленными безопасными углами. Длина — 30 см. цвет — прозрачный

000739

Линейка 30см, пластмассовая, прозрачная, арт.СТ-ЛН-31,32,33, ст.20

25.72 р.

Купить

+ 1 шт

+ 5 шт

+ 10 шт

шт.
×
25.72
р.

Итого:
25.72
р.

В корзину

Показать отфильтрованные товары ()

Дополнительные товары

цена от 25.72 р.

000739

Линейка 30см, пластмассовая, прозрачная, арт.СТ-ЛН-31,32,33, ст.20

25.72 р.

Купить

+ 1 шт

+ 5 шт

+ 10 шт

шт.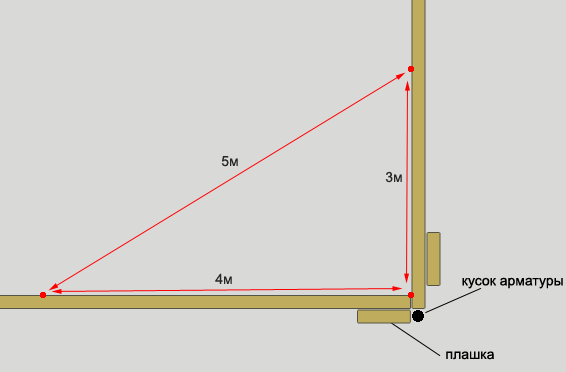
×
25.72
р.

Итого:
25.72
р.

В корзину

×

Деревянный треугольник предназначен для чертежных работ.

023001

Угольник 11см, 45*45, деревянный, ст.1

49.38 р.

Купить

+ 1 шт

+ 5 шт

+ 10 шт

шт.
×
49.38
р.

Итого:
49.38
р.

В корзину

Показать отфильтрованные товары ()

Дополнительные товары

цена от 49.38 р.

023001

Угольник 11см, 45*45, деревянный, ст. 1

49.38 р.

Купить

+ 1 шт

+ 5 шт

+ 10 шт

шт.
×
49.38
р.

Итого:
49.38
р.

В корзину

×

Предназначены для чертежных работ.

026308

Угольник 23см, Можга, ст.1

49.81 р.

Купить

+ 1 шт

+ 5 шт

+ 10 шт

шт.
×
49.81
р.

Итого:
49.81
р.

В корзину

Показать отфильтрованные товары ()

Дополнительные товары

цена от 49. 81 р.

026308

Угольник 23см, Можга, ст.1

49.81 р.

Купить

+ 1 шт

+ 5 шт

+ 10 шт

шт.
×
49.81
р.

Итого:
49.81
р.

В корзину

×

Безупречное качество пластика. Безопасные закругленные углы. Легкий корпус, ровная четкая миллиметровая шкала. Удобный держатель. Длина — 30 см. Цвет — прозрачный флуоресцентный

016853

Линейка 30см, пластмассовая, флюоресц, с держателем, Стамм, ст.20

71.03 р.

Купить

+ 1 шт

+ 5 шт

+ 10 шт

шт.
×
71. 03
р.

Итого:
71.03
р.

В корзину

Показать отфильтрованные товары ()

Дополнительные товары

цена от 71.03 р.

016853

Линейка 30см, пластмассовая, флюоресц, с держателем, Стамм, ст.20

71.03 р.

Купить

+ 1 шт

+ 5 шт

+ 10 шт

шт.
×
71.03
р.

Итого:
71.03
р.

В корзину

×

Деревянная линейка для выполнения различных чертежных работ.

013229

Линейка 50см, деревянная, арт.ЛП, ст.50

65.14 р.

Купить

+ 1 шт

+ 5 шт

+ 10 шт

шт.
×
65.14
р.

Итого:
65.14
р.

В корзину

Показать отфильтрованные товары ()

Дополнительные товары

цена от 65.14 р.

013229

Линейка 50см, деревянная, арт.ЛП, ст.50

65.14 р.

Купить

+ 1 шт

+ 5 шт

+ 10 шт

шт.
×
65.14
р.

Итого:
65.14
р.

В корзину

Далее >

Сколько градусов в угле: как разобраться без транспортра

Метки

Лайфхаки Математика Учеба

Как хотя бы примерно определить, сколько градусов в угле, если под рукой нет ни транспортира, ни угольника? «Так Просто!» знает остроумный способ и просто не может не поделиться им с читателями.

© Depositphotos

Сколько градусов в угле

Общепринятой единицей измерения плоских углов является градус. Почему математики древности выбрали именно такую единицу и почему в окружности 360 градусов, а не, скажем, 1000, точно неизвестно.

View this post on Instagram

A post shared by Математика — легко | ОГЭ | ЕГЭ (@_math_is_easy_)

Одна из гипотез усматривает тут связь с тем, что в году приблизительно 360 дней. Другая гласит, что шумеры выбрали число 360, основываясь на своей шестидесятеричной системе счисления.

Так или иначе, а углы присутствуют не только на страницах учебников, но и повсеместно окружают нас в реальной жизни. Прямой угол легко найти в очертаниях зданий, изгибах мебели и каждом печатном листе.

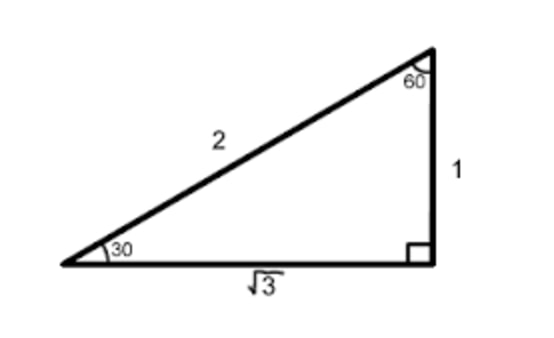
Без угла в 45 градусов ни один столяр не смастерит простейшую рамку. Угол в 60 градусов требуется для построения равносторонних треугольников. Угол 30 градусов используется редко, но помогает получить угол в 120 градусов, необходимый для построения правильного шестиугольника.

Измеряем угол без транспортира

При наличии транспортира всё просто. Размести его центр в вершине угла, а основание совмести с одной из сторон. Проследи за второй стороной угла. В том месте, где она пересечет дугу транспортира, и будет указана величина угла в градусах.

Без транспортира под рукой, как обычно и бывает, задача усложняется. Но смекалка выручит нас и здесь. Вытяни руку ладонью вверх и максимально расставь пальцы.

Следи за тем, чтобы большой палец находился перпендикулярно мизинцу. Тогда, если мизинец указывает на 0 градусов, то безымянный будет указывать на 30, средний на 45, указательный на 60, а большой на 90 градусов.

© Depositphotos

Способ, конечно, не очень точный, но всегда поможет приблизительно понять, с каким углом ты имеешь дело. Раньше мы рассказывали о полезном для каждого домашнего мастера угле в 22,5 градуса, который позволяет правильно заточить ножи. Выдержать его поможет сложенный вчетверо лист бумаги.

Строим углы в 90, 60 и 30 градусов без транспортира

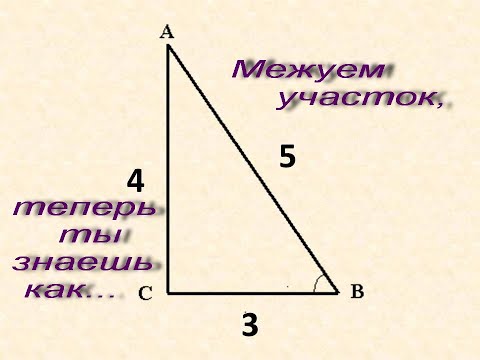
Если нужен угол в 30, 60, 90 градусов, а транспортира или шаблона под рукой нет, помогут эти простые способы. Чтобы получить точный угол в 90 градусов, построй Пифагоров треугольник со сторонами, кратными 3,4,5.

Для этого, например, начерти отрезок длиной 5 см и проведи из его концов дуги с радиусами 3 и 4 см. Теперь соедини точку их пересечения с концами отрезка. Получится прямоугольный треугольник и угол, расположенный напротив гипотенузы, будет составлять ровно 90 градусов.

Когда уже есть прямой угол, легко получить углы в 30 и 60 градусов поможет магическое число 173 (его хорошо бы запомнить). Отложи по одной стороне прямого угла отрезок в 100 мм, а по другой — 173. Соедини их концы. Ты получишь шаблон с углами 90, 60 и 30 градусов!

Поделиться

Теорема Пифагора и закон косинусов – GeoGebra

Автор:

Грег Петрикс

Тема:

Косинус, геометрия

90 014 Теорема Пифагора — одна из важнейших теорем геометрии. Чтобы напомнить вам:
Теорема Пифагора: Если один из углов треугольника равен 90 градусов, то квадрат длин двух катетов по обе стороны от угла 90 градусов в сумме равен квадрату длины стороны, противоположной 90 градусам.угол 0 градусов. Другими словами, если треугольник ABC имеет угол 90 градусов при вершине C, стороны a и b примыкают к C, а сторона c противоположна углу C, то .
Обычно стороны по обе стороны от угла 90 градусов называются «ногами», а сторона, противоположная углу 90 градусов, называется «гипотенуза». Используя эти термины, теорему Пифагора можно сформулировать более гладко:
Теорема Пифагора (переформулированная с новой терминологией): Два катета a и b и гипотенуза c прямоугольного треугольника всегда удовлетворяют
Теорема Пифагора особенно полезна, потому что, если вы знаете любые две стороны прямоугольного треугольника, вы можете использовать приведенное выше уравнение, чтобы найти третью.
Например, если a=3 и b=4, вы можете решить уравнение для c:
Теорема Пифагора полезна, потому что она применима к все прямоугольных треугольников на плоскости. Это утверждение верно в бесконечном множестве различных случаев. Чтобы понять это, посмотрите этот апплет, который динамически иллюстрирует теорему Пифагора, показывая, что a ² и b ² всегда равны c ² . Отрегулируйте синие точки в вершинах прямоугольного треугольника в правой части экрана и обратите внимание, что равенство между a ² +b ² и c ² всегда выполняется независимо от того, как вы настраиваете точки.

Теорема Пифагора чрезвычайно полезна. Во многих реалистичных сценариях можно легко измерить a и b, но часто бывает трудно измерить c. Например, c может проходить через озеро или частную собственность или может находиться в воздухе! Мы вместе решим несколько головоломок в классе, чтобы показать вам, как это работает.

Тем не менее, теорема Пифагора по-прежнему накладывает существенные ограничения на полезность. В частности, требуется, чтобы угол между a и b был равен 90 градусов. Если угол не 90 градусов, теорема Пифагора не поможет.
Здесь вступает в действие закон косинусов. Закон косинусов позволяет нам найти c, даже если угол между a и b не равен 90 градусам. Посмотрите на этот апплет, который иллюстрирует связь между a ² и b ² и c ² , который также принимает во внимание угол C (обратите внимание, что угол написан с большой буквы C, чтобы отличить его от нижнего регистра c, сторона, противоположная углу в) между ножками а и б.
Отрегулируйте синие точки в треугольнике в правой части экрана, чтобы увидеть взаимосвязь. Вначале, когда угол С равен 90 градусов, a ² +b ² точно равно c ² . Однако, когда вы перемещаете любую из трех вершин треугольника, обратите внимание, что сохраняется равенство , а не . Проблема в том, что угол C становится , а не 90 градусов.
Закон косинусов приспосабливается к другим углам в C, кроме угла 90 градусов. Конкретно:
Отняв 2*a*b*cos(C) от a ² +b ² , мы получим ровно c ² . Это закон косинусов , и это чрезвычайно полезно. Это была формула, стоявшая за нашими «загадочными числами» в проектах 2 и 3.

Несколько замечаний:

• Не нервничайте, если не знаете, что такое cos(C). А пока просто подумайте об этом как о числе. Вы можете вычислить его любым количеством способов, но я рекомендую просто погуглить. Например, проверьте эту ссылку, чтобы вычислить косинус 108 градусов. Только не забудьте добавить в поиск «градусы».
• Когда C меньше 90 градусов, косинус положителен (попробуйте несколько вычислений в Google, подобных этому), поэтому -2*a*b*cos(C) равно отрицательное , и, таким образом, кое-что отнимает от ² +b ²
• С другой стороны, когда C больше 90 градусов, косинус отрицателен (опять же, попробуйте несколько вычислений, подобных этому). ), поэтому -2*a*b*cos(C) равно положительному и добавляет что-то к a ² +b ²

Что означает «квадрат» в деревообработке?

Последнее обновление: 1 июня 2022 г.

Нажмите выше, чтобы посмотреть видео

Что такое квадрат?

Идея «квадрата» жизненно важна для деревообработки. Имеется в виду квадратный угол, равный 90 градусам. Таким образом, когда два куска дерева соединяются вместе, образуя угол в 90 градусов, не только этот угол является квадратным, но и говорят, что они перпендикулярны друг другу.

Когда поверхность куска дерева образует угол 90 градусов с его краем, это также квадрат. Если все грани и края куска дерева или изделия составляют 90 градусов, этот кусок или изделие также называют квадратным.

Получение прямых углов в проекте важно для подгонки различных деталей. Вы хотите учесть это в проекте. В противном случае, если вам нужны квадратные 90-градусные углы, а вы ошиблись, то проект не стыкуется должным образом.

Измерение площади

Типы квадратов

Существует несколько распространенных инструментов для измерения площади. Первым и, вероятно, самым старым является квадрат попытки. Этот инструмент прост и состоит из 2 частей; запас и язык. Поместите его под углом либо внутри, либо снаружи, и если детали совмещаются поперек язычка и ложи без зазоров, угол будет квадратным — при условии, что этот инструмент на самом деле квадратный.

Пробный угольник также отлично подходит для разметки линии, перпендикулярной кромке. Приклад сделан толще язычка, чтобы он прилегал к краю. Если край прямой и перпендикулярен поверхности, на которой вы делаете разметку, вы можете провести по нему квадратную линию. Мы делаем это, чтобы отметить для поперечных разрезов.

Существуют также такие инструменты, как скоростной угольник, которые немного отличаются от пробного угольника тем, что они могут выполнять некоторые другие столярные измерения, но не могут измерять внешний угол.

Комбинированный угольник — самый универсальный инструмент из всех, но я обнаружил, что вам придется потратить немало денег, чтобы получить хороший, если вы не можете найти хороший подержанный.

Комбинированный угольник может делать все то же, что и пробный угольник, но у него также есть край под углом 45 градусов для отметки этих углов, и его можно отрегулировать до определенной длины и использовать для измерения других частей, которые должны иметь такую ​​же длину. Его также можно использовать для рисования линии, параллельной краю.

Это столярный угольник, но он не самый лучший для работы по дереву. Я использую свой время от времени для более длительных измерений, но не очень часто. У него нет башмака, который цепляется за край, поэтому его сложно расположить и быть точным.

Самый большой квадрат, который у меня есть, это Т-образный квадрат. Они используются для гипсокартона, но они также отлично подходят для фанеры.

У всех этих инструментов есть свое предназначение, но они не очень полезны, если сами по себе не квадратные.

Проверка квадратности инструмента

Есть быстрый способ «проверить квадрат». Найдите кромку, о которой вы знаете, что она прямая и плоская, как заводская кромка куска фанеры. Вы даже можете поместить линейку, например линейку из квадрата комбинации, на ребро и убедиться, что нет зазоров.

Поднесите квадрат к нему и нарисуйте линию. Теперь переверните квадрат и нарисуйте вторую линию, касающуюся первой. Если линии вообще расходятся друг от друга, то ваш квадрат не… ну, квадрат. Опять же, это предполагает, что край, который вы используете, прямой и плоский.

Close, вероятно, достаточно близко, но если оно значительно отличается, используйте другой квадрат. Есть способы попробовать настроить некоторые из них, но я бы просто использовал другой.

Поделиться этой статьей

Не тратьте деньги на инструменты, которые вам не нужны

Получите мою бесплатную загрузку , в которой перечислены точные инструменты и материалы, необходимые для создания удивительных проектов

…для новичка в мастерской по деревообработке

Пожалуйста, включите JavaScript в вашем браузере, чтобы заполнить эту форму.

Электронная почта *

Мы никогда не разглашаем ваш адрес электронной почты, и вы можете отказаться от подписки в любое время.

Рекомендуемое чтение