Урок по теме «Угол. Прямой угол». 1-й класс
Вид урока: урок изучения и первичного закрепления новых знаний.
Цель: формирование общего понятия об угле, прямой угол.
Задачи:
Образовательная:
– учить различать прямой;
– учить строить прямой угол;
Развивающая:
– развивать познавательный интерес, умение сопоставлять и сравнивать, обобщать;
– развивать творческое мышление, внимание, воображение учащихся, интерес к
математике.
Воспитывающая – воспитание аккуратности, сплоченности, добросовестного
отношения к труду.
Оборудование: таблички со словами: “геометрия, луч, вершина, сторона,
прямой угол”; рисунки домиков, выставка книг Житомирский, Шеврин “Путешествие по
стране Геометрии”, “Все обо всем”; для учеников: угольник, лист бумаги,
компьютер; презентация Power Point.
Ход урока
I. Организационный момент.
Организационный момент.
Ну-ка проверь, дружок,
Ты готов начать урок?
Все ль на месте, Все ль в порядке,
Ручка, книжка и тетрадка?
Все ли правильно сидят?
Все ль внимательно глядят?
Каждый хочет получать
Только лишь оценку “5”.
От кроем тетради и запишем число.
1) Минутка чистописания “Гусеница-растеряша”.
– Гусеница растеряла числа, посмотрите на оставшиеся, разгадайте по какому
правилу можно продолжить ряд чисел. (Дети называют правило: это четные числа;
каждое последующее число на 2 больше предыдущего). Допишите.
– Какие же числа растеряла гусеница? (2, 4, 6, 8, 10, 12, 14, 16 и т. д.)
II. Устный счет.
1) Индивидуальная работа по карточкам.
2) Игра “Математический баскетбол”.
– Любой из вас забьет гол, если правильно решит пример. (Дети по цепочке
решают примеры. )
)
30 + 7
25 + 5
32 – 12
66 + 4
80 – 7
28 – 10
45 – 45
53 + 7
59 – 9
90 + 9
3) Решение задач.
– В саду росли 2 березы, 4 яблони, 5 вишен. Сколько всего фруктовых
деревьев росло в саду?
– Сестре 9 лет, брату 3 года. На сколько сестра будет старше брата через 5
лет?
– Посмотрите на фигуры. Как назвать их одним словом? Почему? (Геометрические
фигуры.)
– Вы сказали “геометрические”? А от какого слово оно произошло? (Геометрия.)
– А что такое геометрия?
| ГЕОМЕТРИЯ |
– Табличка с этим словом вывешивается на доске.
– Слово геометрия пришло из греческого языка. “Ге” – земля “метрио” – мерить.
Геометрия – это раздел математики, в котором изучают фигуры, их
формы, положение предметов в пространстве.
– На какие группы можно разделить все фигуры?
(В первую группу фигуры 1, 3, 5; во вторую – фигуры 2, 4.)
– Что общего между фигурами каждой группы? (I группа – есть углы; II
группа – нет углов.)
III. Работа над новым материалом
Как вы думаете, о чем мы сегодня будем говорить?
Сегодня на уроке мы поговорим об углах, познакомимся с прямым углом, их
свойствами, научимся их обозначать буквами. Все ли углы в фигурах первой группы
одинаковы? (Нет.)
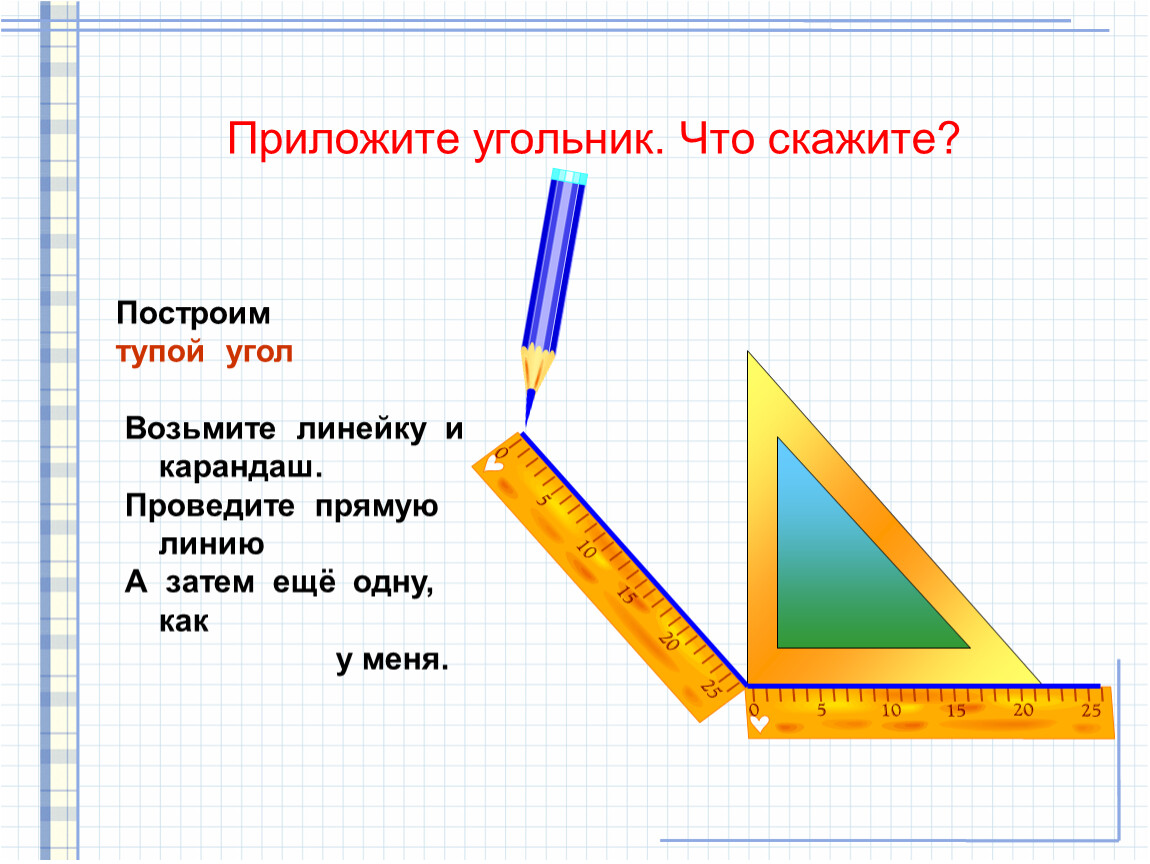
1) Практическая работа. Построение модели
прямого угла.
Какие бывают углы? Углы бывают разные, но сначала мы познакомимся с самым
главным углом. Сейчас мы сложим модель угла, а вы скажите какой это угол.
Возьмет лист бумаги, который лежит на парте.
Согните лист, как на рисунке 1. Согните еще раз, как на рисунке 2. Получилась
модель прямого угла.
рис. 1
рис. 2
2
рис.3
рис.4
Обведите линии сгиба карандашом. На сколько частей прямые линии разделили
плоскость? (На четыре.)
– Сколько углов получилось? (Четыре.)
– Это особенные углы.
– На пересечении линий сгиба поставьте точку. Обозначьте один прямой угол
буквами. Заштрихуйте цветным карандашом его внутреннюю часть.
Может быть, кто-то знает название этих углов? (Эти углы прямые.)
Покажите стороны прямого угла и вершину.
Дети показывают.
| ВЕРШИНА СТОРОНА |
Где в жизни мы встречаемся с прямыми углами?
Моделью прямого угла является также прямой угол чертежного треугольника.
Найдите на нем с помощью своей модели прямой угол.
Прямой угол на чертежном треугольнике – это модель прямого угла.
2) Знакомство с угольником.
Рассмотрите чертежный треугольник. Вы уже убедились, что у него один угол
Вы уже убедились, что у него один угол
прямой.
С помощью модели прямого угла узнайте, будут ли прямыми остальные углы этого
треугольника.
Какие у вас получились углы? (Меньше прямого.)
Работа в тетради.
С помощью угольника удобно не только определять прямые углы, но главное –
строить их. Построим прямой угол в тетради, каждый сам назовет его тремя
буквами.
(Учитель на доске, а дети в тетрадях строят прямой угол. Выполняется
взаимопроверка в парах.)
Что есть у угла? (Вершина, две стороны.)
– С помощью линейки-угольника проверьте работу друг друга в парах. Определить
угол сначала “на глаз”, потом проверить с помощью угольника. Чтобы определить
вид угла, надо совместить его вершину и сторону соответственно с вершиной и
стороной прямого угла на угольнике.
– Как вы думаете, как образовались углы? Как отличить два угла друг от друга?
Давайте сформулируем правило. Что такое угол?
Что такое угол?
Угол – это геометрическая фигура, образованная двумя разными лучами с
общим началом.
– Точка О – вершина угла. Угол можно назвать одной буквой, записанной около
его вершины. Угол О. Но может быть несколько углов, имеющих одну вершину. Как
быть тогда?
– В таких случаях если называть разные углы одной буквой, то будет непонятно,
о каком угле идет речь. Что этого не произошло, на каждой стороне угла можно
отметить по одной точке, поставить около нее букву и обозначить угол тремя
буквами, при этом всегда в середине записывают букву, обозначающую вершину угла.
Угол АОВ. Лучи АО и ОВ – стороны угла.
Обратите внимание угол выделяется дугой.
IV. Актуализация знаний. Повторение изученного.
1) Работа по учебнику. Стр.38 № 2. Запиши различное название углов.
Назови их вершины и стороны.
– Рассмотрите рисунки. Какое правило работы важно помнить, при определении
вида угла с помощью линейки-угольника? (Нужно совмещать вершину и одну сторону
угла с вершиной и стороной прямого угла на линейке-угольнике. )
)
V. динамическая пауза.
Физкультминутка “Буратино”.
Буратино потянулся, раз нагнулся, два нагнулся
Руки в стороны развел, ключик, видно не нашел.
Чтобы ключик нам достать, нужно на носочки встать.
2) Работа в учебнике.
Стр. 40 № 8.
1) Игра “Самый внимательный”.
– Посмотрите внимательно на рисунок, части всех предметов похожи на какие-то
геометрические фиуры.
– Самый внимательный из вас найдет на рисунке нужные предмет. Подсказку ищите
в верхнем правом углу. (Дети указкой показывают треугольник в квадрате.)
А кто подскажет, если здесь прямые углы?
VI. Итог урока. Рефлексия.
– Кто доволен своей работой на уроке? Прикрепите на нашей полянке красный
цветочек.
– Кто считает, что работал не во всю силу и хотел бы на следующий раз
работать лучше – желтый цветочек.
– Кто не доволен своей работой – синий цветочек.
– Посмотрите, какая полянка у нас получилась. Я вижу, что в основном дети
старались и работали хорошо.
Д/з. Стр. 40 № 11. Придумайте и нарисуйте различные
предметы, используя круги, овалы, точки, лучи и углы.
– Что вы узнали нового, интересного? С чем познакомились? Выставить оценки.
– Какое задание понравилось больше всего?
Спасибо за урок.
Конспект урока математики 2 класс » Угол. Прямой угол»
Тема: Угол. Прямой угол.
Данный
урок разработан и проведён в рамках деятельности творческой группы
«Современные педагогические технологии» с целью демонстрации опыта работы
по применению деятельностной технологии в начальной школе по образовательной
системе « Гармония» во 2 классе, автор учебника Н.Б. Истомина
Цель:
Сформировать
представление об угле и его элементах, способность к распознаванию и
обозначению углов;
Познакомить
с понятием «прямой угол»;
Учить
находить прямой угол с помощью чертёжного угольника;
Пополнять
активный запас детей; учить работать в паре;
Развивать
математическую речь, мыслительные операции;
Формировать
познавательный интерес;
Способствовать
здоровьесбережению детей;
Тип
урока: ОНЗ.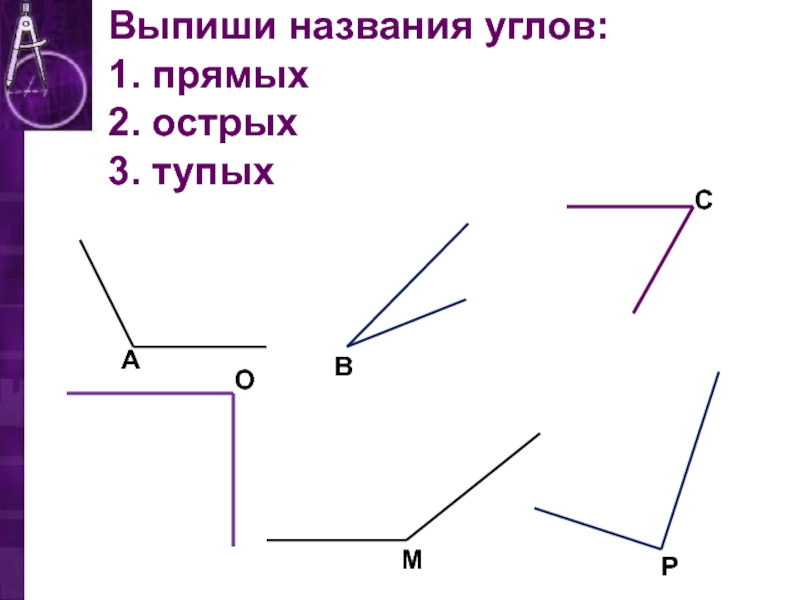
Мыслительные
операции, необходимые на этапе проектирования: анализ,
синтез, обобщение.
Ход
урока
I.
Мотивация к учебной деятельности.
Цель:
создать условия для возникновения внутренней потребности включения в
учебную деятельность.
– Начать
наш урок мне хочется с высказывания американского математика Айвена
Нивена.
(слайд
2)
Математику
нельзя изучать наблюдая, как это делает сосед.
А. Нивен
–
Прочитайте его .
– Как
вы понимаете смысл этих слов? (Если смотреть, как другие анализируют,
сравнивают, преодолевают какие-то трудности, а сам ты этого ничего не
делаешь. То математику знать не будешь).
–
Верно, я думаю, что сегодня на уроке вы успешно преодолеете все трудности,
которые возникнут перед нами.
–
Посмотрите, это … (Ёлочка. )
)
(Слайд 3)
– Что
необычного в изображении ёлочки? (Она составлена из геометрических фигур.)
–
Назовите их. (Треугольники и прямоугольник.)
– А
ведь ёлочка нам подсказывает, какому разделу математики будет посвящён наш
урок. (Геометрии.)
– Да,
и сегодня вам предстоит узнать новое из области геометрии.
–
Молодцы! С чего начнём? (С повторения необходимого.)
II.
Актуализация знаний и фиксация затруднения в деятельности.
Цель:
активизировать представление о
плоскости и луче;
тренировать
умения чертить, обозначать и называть лучи;
активизировать
мыслительные операции: анализ, синтез, обобщение;
организовать
самостоятельное выполнение учащимися индивидуального задания на применение
нового знания, запланированного для изучения на данном уроке;
организовать
фиксацию учащимися возникшего затруднения в обосновании правильности
полученного результата.
(Слайд
4)
–
Посмотрите,
нас встречают жители этой страны.
–
Назовите их одним словом. (Геометрические фигуры)
–
Назовите многоугольники ( треугольник, квадрат, прямоугольник)
(
Слайд 5)
– Назовите
геометрическую фигуру, которая состоит из 4-х звеньев
( незамкнутая
ломаная линия) ( Слайд 5)
– Какая
геометрическая фигура не имеет ни начала, ни конца? (прямая линия)
(Слайд
6 )
–
Часть
прямой, ограниченная с двух сторон, называется…. (отрезок)
(Слайд
7 )
–
А как называется оставшаяся фигура? (Луч) ( Слайд 8)
– Что
вы знаете о геометрической фигуре луч? (Луч – это часть прямой,
ограниченная с одной стороны)
– Чем
отличается луч от прямой? (Луч– это часть прямой, ограниченная с одной
стороны, а прямая не имеет ни начала ни конца).
–
У
вас на партах лежат модели лучей.
–
Покажите точку, начало луча, покажите весь луч.
–
Сравните
лучи АВ и АС.
–
Что у них общего? (У них общее начало точка А)
–
Возьмите модели лучей и наложите их друг на друга так, чтобы точки А совпали,
а части прямой расходились в разные стороны.
–
На сколько частей лучи разделили плоскость? (На 2 части)
–
Как бы вы назвали меньшую из этих частей? (Углом) (Слайд 9)
–
Как докажете, что данная фигура является углом?
Дети
обосновывают своё мнение и приходят к выводу, что не могут доказать, что
данная фигура является углом.
– Почему
же возникло затруднение при доказательстве того, что выбранная вами фигура
угол? (Нам неизвестно, что такое угол, каковы признаки этой
геометрической фигуры.)
–
Молодцы! Поняв причину, дальше надо … (Поставить цель, выяснить, что
такое угол, выявить его признаки. )
)
–
Назовите тему урока. (Угол.) (Слайд 10)
Открыть
часть темы на доске.
III.
«Открытие» нового знания.
Цель:
организовать
построение нового знания об угле;
организовать
фиксацию нового знания в речи;
организовать
выполнение задания, вызвавшего ранее затруднение;
зафиксировать
преодоление возникшего ранее затруднения
–
Покажите точку, общее начало лучей.
–
Посмотрите, как называется общее начало лучей. (Это вершина угла) (слайд
11)
–
Покажите
лучи, которые образуют угол.
–
Как их называют? (Стороны угла.)
–
Сколько вершин у угла? (1)
–
Сколько сторон у угла? (2)
– Так
из чего состоит угол? (Из точки – вершины и двух лучей – сторон, которые
выходят из этой точки — вершины)
– Кто
может сказать, что же такое угол? (Угол – это геометрическая фигура,
которая состоит из точки — вершины и двух лучей — сторон, которые выходят
из этой точки)
–
Какие новые слова добавили бы в геометрический словарь? (Угол, вершина
угла, сторона угла).
– Вы конечно
знаете, что у каждой геометрической фигуры есть имя, и у углов тоже есть
имя.
–
Вас называют разными именами.
–
И угол тоже можно назвать по-разному.
–
Прочитайте об этом в учебнике на стр. 85.
– Что
интересного заметили при чтении имён угла? (Буква, которая называет
вершину читается в середине)
–
Записывают
это так: слово «угол» заменяют специальным знаком:
–
Запишем этот знак в тетради.
–
Начинаем писать с верхнего правого угла клетки, ведём наклонную в нижний
левый угол клетки и вправо по нижней стороне клетки в нижний правый угол. (Дети
записывают знак в тетради)
–
Как
пишется ваше имя?
– А
теперь обратите внимание на то, как пишется имя угла. (Все буквы
заглавные)
– Как
вы думаете, почему так записывают угол? (По названию вершины угла. )
)
–
Правильно. Запишите имя угла в тетради.
—
Запишите название вашего угла ( ВАС)
ФИЗМИНУТКА
«Открытие»
нового знания (продолжение)
2. Цели:
организовать
построение нового знания о прямом угле;
организовать
фиксацию нового знания в речи.
–
Скажите, а можно ли угол сделать больше или меньше по размеру?
(слайд
12)
– Смоделируйте
полученный угол так, чтобы он стал меньше, а теперь, чтобы он стал больше.
–
Какой вывод можем сделать о размере углах? (Углы бывают разные по
размеру)
–
Верно, углы бывают разные, и наша задача узнать, какой угол самый главный.
Учебник
, стр. 84 № 265 работа в парах
–
Сложите лист бумаги пополам, а потом ещё раз пополам.
–
Возьмите линейку и красный карандаш, проведите линии сгиба.
–
На сколько частей прямые разделили плоскость? (на 4 части)
–
Что можете сказать о прямых? (Они пересекаются)
–
Сколько углов образовали пересекающиеся прямые? (4)
–
Эти пересекающиеся прямые образовали особенные углы.
–
Может кто-нибудь знает названия этих углов?
–
Это прямые углы (слайд 13)
–
Покажите пальчиком каждый прямой угол.
–
Раскрасьте прямые углы разными цветами.
–
Поставьте точку на пересечении прямых.
–
Чем будет являться эта точка для каждого из углов? (Вершиной угла)
(слайд
14)
–
Покажите,
где в жизни встречается прямой угол?
Стр.86
–
Ребята, а вы обратили внимание, что у вас на партах лежит ещё один
чертёжный инструмент.
–
Кто знает, как он называется?
–
Правильное его название чертёжный угольник.
–
Прямые углы удобно находить и строить с помощью угольника.
–
Рассмотрите его внимательно и подумайте, почему?
–
Итак, какова наша задача? (Научиться с помощью угольника чертить и определять
прямые углы.)
(слайд
15)
–
Составим
алгоритм.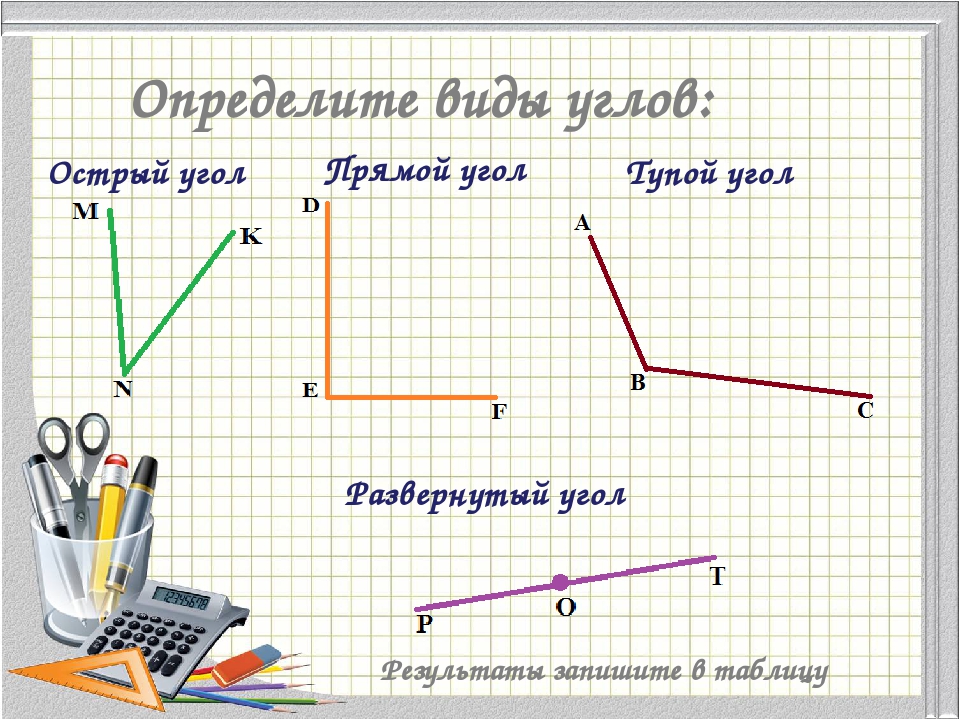
Совместить
вершину прямого угла чертёжного угольника и вершину угла.
Совместить
одну из сторон чертёжного угольника и сторону угла.
Если
вторая сторона угла совпала со второй стороной угольника, то это прямой
угол.
—
Найдите прямые углы в окружающей нас обстановке.
–
Начертите и обозначьте прямые углы с помощью чертёжного угольника.
— Как
без помощи угольника можно построить или определить прямой угол?
IV.
Самостоятельная работа c самопроверкой.
Цель:
организовать самостоятельное выполнение учащимися типовых заданий на
применение новых знаний.
Работа
по учебнику с. 85 №266
Проверка
работы с помощью доски.( Слайд 16)
Если
останется время:
—
Определите с помощью угольника прямые углы, поставьте +.
– Самостоятельно
проверьте, так ли вы нашли прямые углы, если так, поставьте «+».
–
Каким новым понятием пополнился наш словарь? (чертёжный угольник).
–
Какие новые жители поселились в стране Геометрия? (угол, прямой угол)
(слайд 17)
–
Посмотрите на все фигуры (слайд 18) и скажите, какие фигуры имеют
углы?
–
А какие имеют прямые углы?
V.
Рефлексия учебной деятельности на уроке.
Цели:
организовать
фиксацию учащимися степени соответствия поставленной цели и полученного
результата учебной деятельности;
создать
условия для фиксации учащимися в речи нового знания, изученного на уроке:
что такое угол, как определить прямой угол;
организовать
фиксацию затруднений, которые остались, и способов их преодоления;
организовать
самооценку учениками собственной учебной деятельности на уроке;
–
Какую цель вы ставили перед собой на уроке? (Узнать, что такое угол, его
признаки. )
)
–
Достигли цели? Докажите.
– Что
такое угол? (Это меньшая часть плоскости, ограниченная двумя лучами,
имеющими общее начало.)
– Углы
бывают разные. С каким видом угла вы познакомились сегодня? (С прямым
углом.)
– Как
вы находили прямой угол среди углов? (С помощью угольника: совмещали угол и
одну из сторон угольника. Потом смотрели, совпадает ли другая сторона угла
со стороной угольника.)
– Как
записывают название углов? (Пишут значок угла и букву, обозначающую вершину
угла, или три буквы, причём букву, обозначающую вершину, пишут в середине.)
— Сейчас я раздам карточки с названиями профессий людей.
Докажите,
что людям этих профессий нужны знания по данной теме.
ПОВАР
ВОСПИТАТЕЛЬ
ЛЁТЧИК
СТРОИТЕЛЬ
ШВЕЯ
–
Оцените свою работу на уроке.
–
Ответьте на вопросы
УЗНАЛ
Я
ПРЕДСТАВИЛ
СМОГ
—
Встаньте, пожалуйста, те,
кто
устал от сегодняшнего урока;
кому
было трудно;
а
кто был уверен в себе;
у
кого осталось отличное настроение.
Прямоугольный треугольник (определение, свойства, формулы)
Прямоугольный треугольник – это треугольник, один из внутренних углов которого равен 90 градусов или любой из углов является прямым. Поэтому этот треугольник также называют прямоугольным треугольником или 90-градусным треугольником. Прямоугольный треугольник играет важную роль в тригонометрии. Давайте узнаем больше об этом треугольнике в этой статье.
Содержание:
|
Что такое треугольник?
Треугольник – это правильный многоугольник с тремя сторонами, сумма любых двух сторон которого всегда больше третьей стороны. Это уникальное свойство треугольника. Другими словами, можно сказать, что любая замкнутая фигура с тремя сторонами и суммой всех трех внутренних углов равна 180°.
Другими словами, можно сказать, что любая замкнутая фигура с тремя сторонами и суммой всех трех внутренних углов равна 180°.
Будучи замкнутой фигурой, треугольник может иметь разные типы, и каждая фигура описывается углом между любыми двумя соседними сторонами.
Типы треугольников
- Остроугольный треугольник: Если угол между любыми двумя сторонами меньше 90 градусов, такой треугольник называется остроугольным.
- Прямоугольный треугольник: Если угол между парой сторон равен 90 градусов, такой треугольник называется прямоугольным.
- Тупоугольный треугольник: Когда угол между парой сторон больше 90 градусов, такой треугольник называется тупоугольным.
Остальные три типа треугольников основаны на сторонах треугольника.
- Разносторонний треугольник (Все три стороны не равны)
- Равнобедренный треугольник (Две стороны равны)
- Равносторонний треугольник (Все три стороны равны)
Примечание: Разносторонний и равнобедренный треугольники могут быть прямоугольными. У разностороннего прямоугольного треугольника все три стороны неравны по длине, и любой из углов будет прямым. В равнобедренном прямоугольном треугольнике основание и перпендикулярные стороны равны по длине, включая прямой угол. Третья неравная сторона будет гипотенузой.
У разностороннего прямоугольного треугольника все три стороны неравны по длине, и любой из углов будет прямым. В равнобедренном прямоугольном треугольнике основание и перпендикулярные стороны равны по длине, включая прямой угол. Третья неравная сторона будет гипотенузой.
Посмотрите видео ниже, чтобы узнать больше о типах треугольников
Прямоугольный треугольник
Прямоугольный треугольник — это тип треугольника, один из углов которого равен 90 градусов. Два других угла в сумме дают 90 градусов. Стороны, включающие прямой угол, перпендикулярны и являются основанием треугольника. Третья сторона называется гипотенузой, которая является самой длинной из всех трех сторон.
Три стороны прямоугольного треугольника связаны друг с другом. Эта связь объясняется теоремой Пифагора. Согласно этой теореме, в прямоугольном треугольнике
Гипотенуза 2 = Перпендикуляр 2 + Основание 2
Для лучшего понимания см.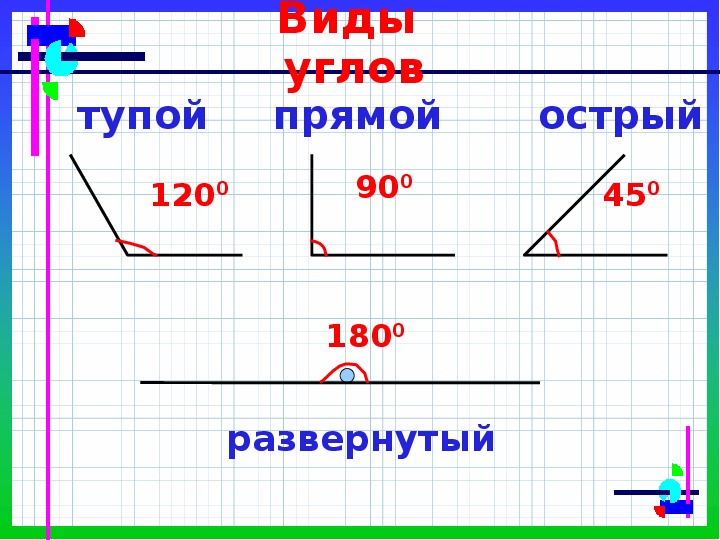 рисунок ниже.
рисунок ниже.
Площадь самого большого квадрата равна сумме квадратов двух других малых квадратов. Мы можем сгенерировать теорему Пифагора, поскольку квадрат длины гипотенузы равен сумме длины квадратов основания и высоты.
Форма прямоугольного треугольника
Прямоугольный треугольник представляет собой трехстороннюю замкнутую фигуру, у которой есть одна перпендикулярная сторона, называемая катетом или высотой треугольника.
Свойства прямоугольного треугольника
Обсудим свойства прямоугольного треугольника.
- Один угол всегда равен 90° или прямому углу.
- Сторона, противоположная углу 90 °, является гипотенузой.
- Гипотенуза всегда самая длинная сторона.
- Сумма двух других внутренних углов равна 90°.
- Две другие стороны, примыкающие к прямому углу, называются основанием и перпендикуляром.
- Площадь прямоугольного треугольника равна половине произведения смежных сторон прямого угла, т.
 е.
е.
Площадь прямоугольного треугольника = ½ (основание × перпендикуляр)
- Если из прямого угла опустить перпендикуляр на гипотенузу, то получится три подобных треугольника.
- Если провести описанную окружность, проходящую через все три вершины, то радиус этой окружности равен половине длины гипотенузы.
- Если один из углов равен 90°, а два других угла равны 45° каждый, то такой треугольник называется равнобедренным прямоугольным треугольником, в котором стороны, прилегающие к 90°, равны по длине.
Выше были общие свойства прямоугольного треугольника. Построение прямоугольного треугольника также очень просто. Продолжайте учиться с BYJU’S, чтобы получить больше таких учебных материалов, связанных с различными темами геометрии и другими субъективными темами.
Площадь прямоугольного треугольника
Площадь находится в двумерной области и измеряется в квадратных единицах. Его можно определить как объем пространства, занимаемый двумерным объектом.
Его можно определить как объем пространства, занимаемый двумерным объектом.
Площадь треугольника можно вычислить по 2 формулам:
\(\begin{array}{l}Площадь= \frac{a \times b }{2}\end{array} \)
А, формула Герона
\(\begin{array}{l}Area= \sqrt{s(s-a)(sb)(s-c)}\end{array} \)
Здесь s — это полупериметр, который рассчитывается как:
\(\begin{массив}{l}s =\frac{a+b+c}{2}\end{массив} \)
Где, a, b, c — стороны треугольника.
Рассчитаем площадь треугольника, используя приведенную ниже цифру.
Рис. 1: Опустим перпендикуляр a к основанию b в данном треугольнике.
Рис. 2: Теперь давайте присоединим еще один треугольник к стороне треугольника. Он образует форму параллелограмма, как показано на рисунке.
Рис. 3: Переместим треугольник красного цвета на другую сторону параллелограмма, как показано на рисунке выше.
Рис. 4: Теперь он принимает форму прямоугольника.
4: Теперь он принимает форму прямоугольника.
Теперь по свойству площади она рассчитывается как произведение любых двух сторон
Следовательно, площадь =b × h (для прямоугольника)
Следовательно, площадь прямоугольного треугольника будет равна половине, т.е.
\(\begin{array}{l}Площадь = \frac{b \times h}{2}\end{array} \)
В прямоугольном треугольнике основание всегда перпендикулярно высоте. Когда стороны треугольника не даны, а даны только углы, площадь прямоугольного треугольника можно вычислить по данной формуле:
\(\begin{array}{l}Площадь = \frac{bc \times ba}{2}\end{массив} \)
Где a, b, c — соответствующие углы прямоугольного треугольника, где ∠b всегда равен 90°.
Периметр
Как известно, три стороны прямоугольного треугольника — это основание, перпендикуляр и гипотенуза. Таким образом, периметр прямоугольного треугольника равен сумме всех трех его сторон.
Периметр прямоугольного треугольника = длина (основание + перпендикуляр + гипотенуза)
Пример: если основание = 4 см, перпендикуляр = 3 см, а гипотенуза = 5 см.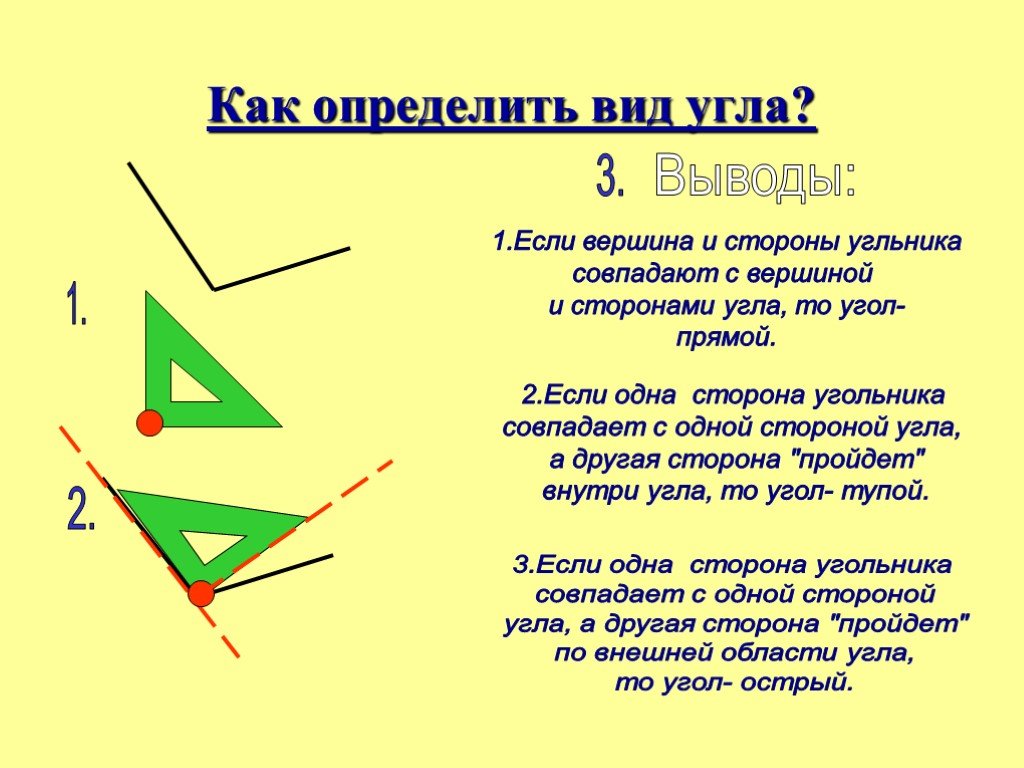 Чему равен периметр прямоугольного треугольника?
Чему равен периметр прямоугольного треугольника?
Периметр = 4 + 3 + 5 = 12 см
Решенные примеры
В.1: В прямоугольном треугольнике, если перпендикуляр = 8 см, а основание = 6 см, то какова величина гипотенузы?
Решение: Дано,
Перпендикуляр = 8 см
Основание = 6 см
Нам нужно найти гипотенузу.
По теореме Пифагора мы это знаем;
Гипотенуза = √(перпендикуляр 2 + основание 2 )
Н = √(6 2 + 8 2 )
= √36 + 64
= √100
= 10 см
Следовательно, гипотенуза прямоугольного треугольника равна 10 см.
В.2: Если гипотенуза равна 13 см, а основание равно 12 см, то найдите длину перпендикуляра прямоугольного треугольника?
Решение: Дано,
Гипотенуза = 13 см
Основание = 12 см
Перпендикуляр = ?
По теореме Пифагора мы знаем, что
Гипотенуза 2 = Перпендикуляр 2 + Основание 2
Перпендикуляр 2 = Гипотенуза 2 – Основание 2
P = √(13 2 – 12 2 )
P = √(169 – 144)
P = √25
П = 5 см
Следовательно, значение перпендикуляра равно 5см.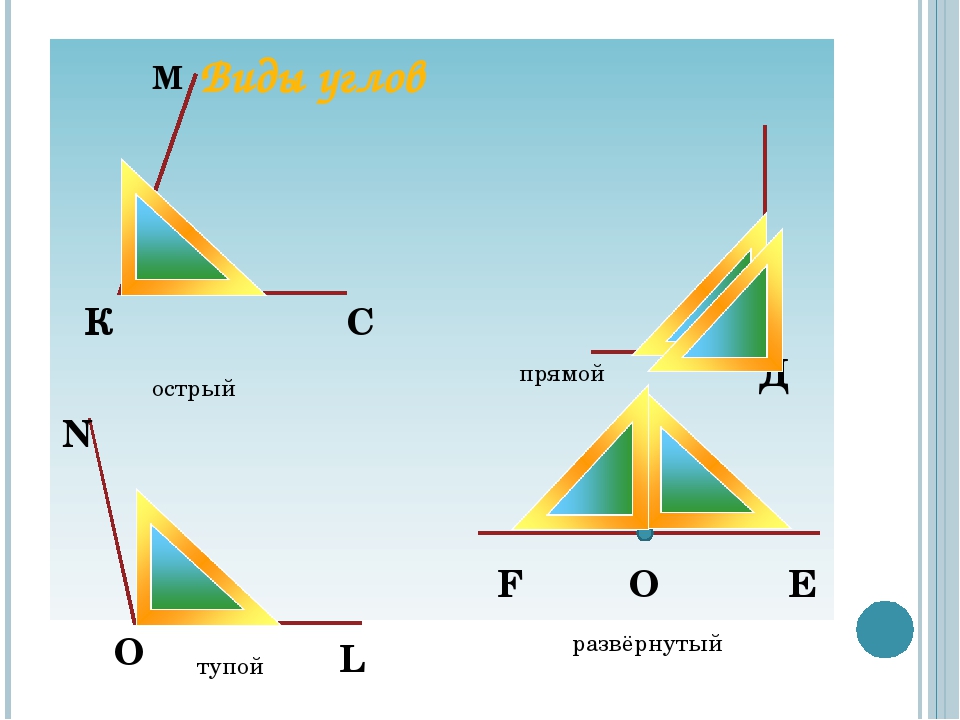
Практические задачи
- Найдите длину перпендикуляра, если прямоугольный треугольник имеет основание в 2 единицы и гипотенузу в √8 единиц.
- Чему равна площадь прямоугольного треугольника с основанием 7 см и гипотенузой 25 см?
- Докажите, что в прямоугольном треугольнике гипотенуза является наибольшей стороной.
Чтобы узнать больше интересных фактов о треугольниках, следите за новостями BYJU’S.
Часто задаваемые вопросы о прямоугольном треугольнике
Q1
Что такое прямоугольные треугольники?
Прямоугольные треугольники — это треугольники, в которых один угол равен 90 градусов. Так как один угол равен 90°, то сумма двух других углов будет равна 90°.
Q2
Как найти недостающую сторону любого прямоугольного треугольника?
Для прямоугольного треугольника можно использовать тригонометрические функции или теорему Пифагора, чтобы найти недостающие стороны. Если даны две стороны, можно использовать теорему Пифагора, а когда даны измерения одной стороны и угла, можно использовать тригонометрические функции, такие как синус, косинус и тангенс, для нахождения недостающей стороны.
Если даны две стороны, можно использовать теорему Пифагора, а когда даны измерения одной стороны и угла, можно использовать тригонометрические функции, такие как синус, косинус и тангенс, для нахождения недостающей стороны.
Q3
Может ли треугольник иметь два прямых угла? Объяснять.
Нет, в треугольнике не может быть двух прямых углов. У треугольника ровно 3 стороны, а сумма внутренних углов равна 180°. Итак, если треугольник имеет два прямых угла, третий угол должен быть равен 0 градусов, что означает, что третья сторона будет пересекаться с другой стороной. Таким образом, треугольника с двумя прямыми углами быть не может.
Q4
Чему равна сумма всех внутренних углов прямоугольного треугольника?
Для любого треугольника сумма всех внутренних углов равна 180 градусам.
Q5
Каковы три стороны прямоугольного треугольника?
Тремя сторонами прямоугольного треугольника являются основание, перпендикуляр и гипотенуза.
Какова формула прямоугольного треугольника?
Мы можем использовать теорему Пифагора, чтобы найти стороны прямоугольного треугольника.
С 2 = А 2 + В 2
Прямоугольный треугольник — Формула, Свойства
Прямоугольный треугольник — это треугольник, в котором один из углов равен 90°. Угол в 90 градусов называется прямым углом, и, следовательно, треугольник с прямым углом называется прямоугольным треугольником . Кроме того, на основании других значений углов прямоугольные треугольники классифицируются как равнобедренные прямоугольные треугольники и разносторонние прямоугольные треугольники. Давайте узнаем больше о свойствах прямоугольного треугольника , частей прямоугольного треугольника вместе с некоторыми 9Примеры 0008 прямоугольных треугольников в этой статье.
1. | Что такое прямоугольный треугольник? |
| 2. | Формула прямоугольного треугольника |
| 3. | Периметр прямоугольного треугольника |
| 4. | Площадь прямоугольного треугольника |
| 5. | Свойства прямоугольного треугольника |
| 6. | Типы прямоугольных треугольников |
| 7. | Часто задаваемые вопросы о прямоугольном треугольнике |
Что такое прямоугольный треугольник?
Прямоугольный треугольник — это треугольник, в котором один угол равен 90°. В этом треугольнике отношения между различными сторонами можно легко понять с помощью теоремы Пифагора. Сторона, противоположная прямому углу, является наибольшей стороной и называется гипотенузой. Обратите внимание на прямоугольный треугольник ABC, приведенный ниже, который показывает основание, высоту и гипотенузу. Здесь АВ — основание, АС — высота, ВС — гипотенуза.
Здесь АВ — основание, АС — высота, ВС — гипотенуза.
Определение прямоугольного треугольника
Определение прямоугольного треугольника гласит, что если один из углов треугольника является прямым углом — 90º, такой треугольник называется прямоугольным или прямоугольным.
Теперь давайте разберемся в отличительных чертах прямоугольного треугольника, относящегося к треугольнику ABC, приведенному выше.
- AC высота, высота или перпендикуляр
- АВ является базовым
- АС ⊥ АВ
- ∠А = 90º
- Сторона ВС, противоположная прямому углу, называется гипотенузой и является наибольшей стороной прямоугольного треугольника.
Примерами прямоугольных треугольников в нашей повседневной жизни являются треугольный кусок хлеба, квадратный лист бумаги по диагонали или треугольная шкала 30-60-90 в геометрической коробке.
Формула прямоугольного треугольника
Согласно теореме Пифагора, в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов двух других катетов. Используя это правило, формулу прямоугольного треугольника можно представить следующим образом: Квадрат гипотенузы равен сумме квадрата основания и квадрата высоты .
Используя это правило, формулу прямоугольного треугольника можно представить следующим образом: Квадрат гипотенузы равен сумме квадрата основания и квадрата высоты .
(Гипотенуза) 2 = (Основание) 2 + (Высота) 2
Тройки Пифагора : Три числа, которые удовлетворяют приведенному выше уравнению, известны как числа Пифагора. тройняшки. Например, (3, 4, 5) является пифагорейской тройкой, потому что мы знаем, что 3 2 = 9, 4 2 = 16 и 5 2 = 25 и 9 + 16 = 25. Следовательно, 3 2 + 4 2 = 5 2 . Любые три числа, которые удовлетворяют этому условию, называются пифагорейскими тройками, такими как 3, 4 и 5. Некоторые другие примеры пифагорейских троек: (6, 8, 10) и (12, 5, 13).
Периметр прямоугольного треугольника
Периметр прямоугольного треугольника равен сумме мер всех трех сторон. Это сумма основания, высоты и гипотенузы прямоугольного треугольника. Обратите внимание на показанный ниже прямоугольный треугольник, в котором периметр равен сумме сторон BC + AC + AB = (a + b + c). Периметр является линейной величиной и представлен линейными единицами, такими как см, дюймы, ярды и т. д.
Обратите внимание на показанный ниже прямоугольный треугольник, в котором периметр равен сумме сторон BC + AC + AB = (a + b + c). Периметр является линейной величиной и представлен линейными единицами, такими как см, дюймы, ярды и т. д.
Площадь прямоугольного треугольника
Площадь прямоугольного треугольника — это пространство, занимаемое треугольником. Он равен половине произведения основания и высоты треугольника. Это двумерная величина и поэтому представлена в квадратных единицах. Две стороны, необходимые для нахождения площади прямоугольного треугольника, — это основание и высота.
Площадь прямоугольного треугольника рассчитывается по формуле: Площадь прямоугольного треугольника = (1/2 × основание × высота)
Свойства прямоугольного треугольника
Первое свойство прямоугольного треугольника состоит в том, что один из его углов равен 90º. Угол 90º является прямым углом и наибольшим углом прямоугольного треугольника.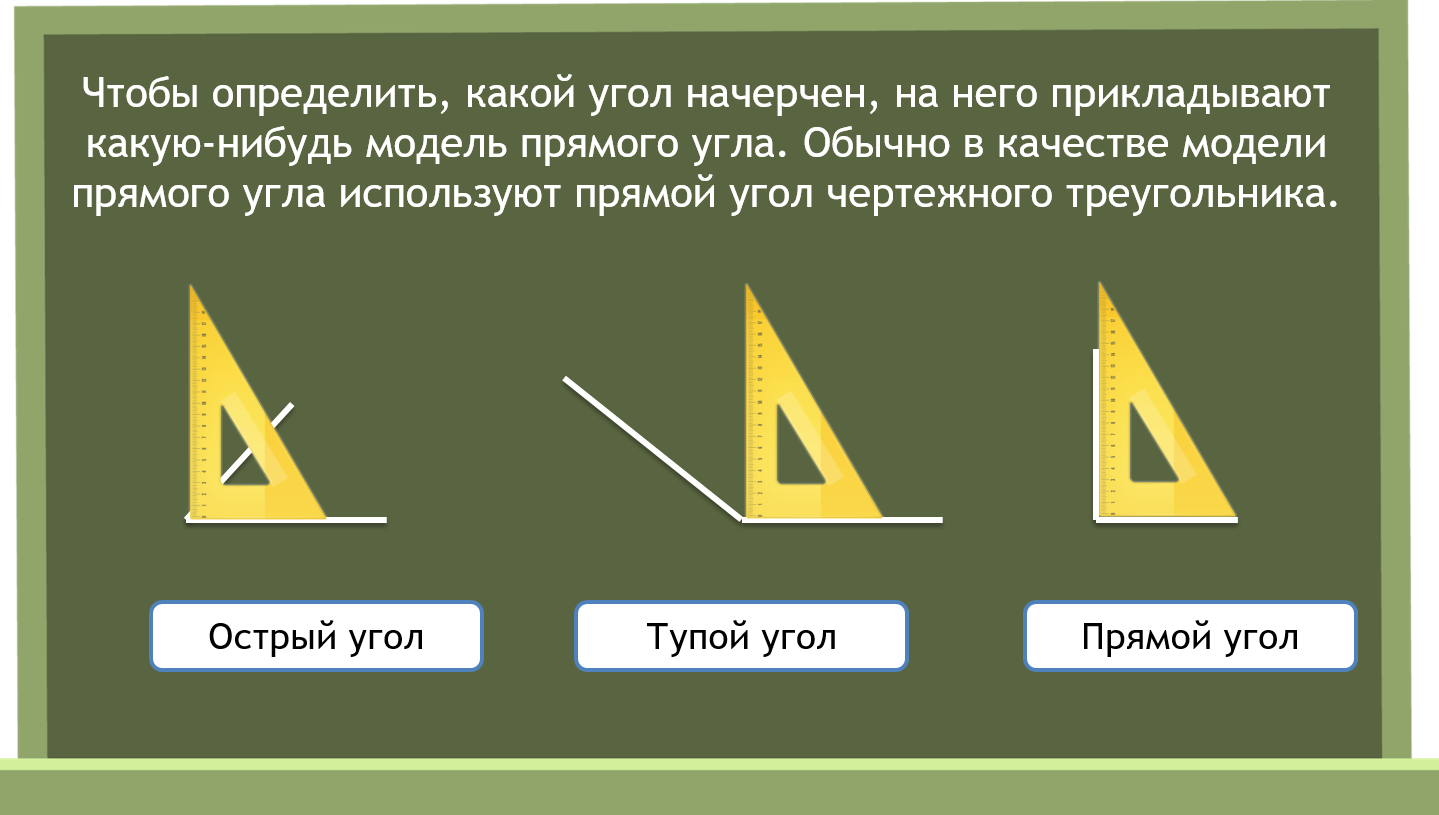 Кроме того, два других угла меньше 90º и называются острыми углами. Свойства прямоугольного треугольника перечислены ниже:
Кроме того, два других угла меньше 90º и называются острыми углами. Свойства прямоугольного треугольника перечислены ниже:
- Наибольший угол прямоугольного треугольника всегда равен 90º.
- Самая большая сторона прямоугольного треугольника называется гипотенузой, которая всегда является стороной, противоположной прямому углу.
- Размеры сторон следуют правилу Пифагора.
- У него не может быть тупого угла.
Типы прямоугольных треугольников
Мы узнали, что один из углов прямоугольного треугольника равен 90º. Это означает, что два других угла в треугольнике будут острыми углами. Есть несколько особых прямоугольных треугольников, таких как равнобедренных прямоугольных треугольников и разносторонних прямоугольных треугольников . Треугольник, в котором один угол равен 90º и два других угла равны, называется равнобедренным прямоугольным треугольником, а треугольник, в котором два других угла имеют разные значения, называется разносторонним прямоугольным треугольником.
Равнобедренный прямоугольный треугольник
Равнобедренным прямоугольным треугольником называется треугольник с углами 90°-45°-45°. Обратите внимание на приведенный ниже треугольник ABC, в котором угол A = 90º, и мы увидим, что AB = AC. Поскольку две стороны равны, треугольник также является равнобедренным. Мы знаем, что сумма углов треугольника равна 180º. Следовательно, сумма углов при основании равна 9.0º, что означает, что они по 45º каждая. Итак, в равнобедренном прямоугольном треугольнике углы всегда равны 90°-45°-45°.
Разносторонний прямоугольный треугольник
Разносторонний прямоугольный треугольник — это треугольник, в котором один угол равен 90°, а два других угла имеют разные измерения. В приведенном ниже треугольнике PQR ∠Q = 90º, следовательно, это прямоугольный треугольник. PQ не равен QR, следовательно, это разносторонний треугольник. Существует также особый случай разностороннего треугольника 30º-60º-90º, который также является прямоугольным треугольником, в котором отношение самой длинной стороны треугольника к его самой короткой стороне составляет 2: 1. Сторона, противоположная углу 30º, является самой короткой стороной.
Сторона, противоположная углу 30º, является самой короткой стороной.
Советы и рекомендации
Здесь перечислены некоторые важные советы и рекомендации, связанные с прямоугольным треугольником.
- Длины сторон прямоугольного треугольника всегда удовлетворяют теореме Пифагора.
- В прямоугольном треугольнике гипотенуза является стороной, противоположной прямому углу, и является самой длинной стороной треугольника.
- Две другие ноги перпендикулярны друг другу; один — основание, а другой — высота.
Важные примечания
- В прямоугольном треугольнике (гипотенуза) 2 = (основание) 2 + (высота) 2
- Площадь прямоугольного треугольника рассчитывается по формуле Площадь прямоугольного треугольника = 1/2 × основание × высота
- Периметр прямоугольного треугольника равен сумме мер всех трех сторон.
- Равнобедренные прямоугольные треугольники имеют углы 90º, 45º, 45º.

☛ Похожие темы
- Гипотенуза
- Пифагорейские тройки
- Формула гипотенузы
Примеры прямоугольного треугольника
Пример 1: Может ли прямоугольный треугольник иметь размеры 11 дюймов, 60 дюймов и 61 дюйм?
Решение:
Если числа 11, 60 и 61 пифагорейские тройки, то они образуют прямоугольный треугольник. 11 2 = 121; 60 2 = 3600; 61 2 = 3721. Мы видим, что: 121 + 3600 = 3721. Следовательно, данные числа являются пифагорейскими тройками и могут быть размерами прямоугольного треугольника. Следовательно, 11 дюймов, 60 дюймов и 61 дюйм могут образовать прямоугольный треугольник.
Пример 2: Найдите площадь прямоугольного треугольника, основание которого равно 12 единицам, а высота 5 единицам.
Решение:
Формула площади треугольника равна 1/2 × b × h.
 Подставляя b = 12 единиц и h = 5 единиц, мы имеем Площадь = 1/2 × 12 × 5 = 30 единиц 2 . Следовательно, площадь прямоугольного треугольника равна 30 квадратных единиц.
Подставляя b = 12 единиц и h = 5 единиц, мы имеем Площадь = 1/2 × 12 × 5 = 30 единиц 2 . Следовательно, площадь прямоугольного треугольника равна 30 квадратных единиц.Пример 3: Укажите истинное или ложное значение прямоугольного треугольника.
а.) В прямоугольном треугольнике гипотенуза является стороной, противоположной прямому углу, и является самой длинной стороной треугольника.
б.) Прямоугольный треугольник может иметь один тупой угол.
Решение:
а.) Верно, что в прямоугольном треугольнике гипотенуза является стороной, противоположной прямому углу, и является самой длинной стороной треугольника.
б.) Неверно, в прямоугольном треугольнике не может быть тупых углов.
перейти к слайдуперейти к слайдуперейти к слайду
Разбивайте сложные концепции с помощью простых визуальных средств.
Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций.
Записаться на бесплатный пробный урок
Практические вопросы по прямоугольным треугольникам
перейти к слайдуперейти к слайду
Часто задаваемые вопросы о прямоугольном треугольнике
Что такое прямоугольный треугольник в геометрии?
Треугольник, в котором одна из мер углов равна 90 градусов, называется прямоугольным треугольником или прямоугольным треугольником.
Какие существуют типы прямоугольных треугольников?
Треугольники классифицируются на основе измерения сторон и углов. Три типа прямоугольных треугольников упомянуты ниже.
- Равнобедренный прямоугольный треугольник — это треугольник, в котором углы равны 90º, 45º и 45º.
- Разносторонний прямоугольный треугольник — это треугольник, в котором один угол равен 90°, а два других острых угла имеют разную величину.
- Треугольник 30º — 60º — 90º — еще один интересный прямоугольный треугольник, в котором отношение самой длинной стороны треугольника к его самой короткой стороне составляет 2:1.

Какова мера углов прямоугольного треугольника?
В прямоугольном треугольнике один из углов равен 90º. Два других угла острые. И все три угла прямоугольного треугольника в сумме дают 180°, как и любого другого треугольника.
Какая формула прямоугольного треугольника?
Формула, которая используется для прямоугольного треугольника, — это теорема Пифагора. Он гласит, что квадрат гипотенузы равен сумме квадратов двух других сторон. Это означает, что (гипотенуза) 2 = (основание) 2 + (высота) 2 .
Как найти площадь прямоугольного треугольника?
Площадь прямоугольного треугольника – это площадь, занимаемая треугольником, и равна половине произведения основания и высоты треугольника. Он двумерный и представлен в квадратных единицах. Формула, которая используется для нахождения площади прямоугольного треугольника: Площадь прямоугольного треугольника = 1/2 × основание × высота 9.0003
Может ли прямоугольный треугольник иметь две равные стороны?
Да, прямоугольный треугольник может иметь две равные стороны. Самая длинная сторона называется гипотенузой, а две другие стороны могут быть равны или не равны друг другу. Прямоугольный треугольник, у которого две стороны равны, называется равнобедренным прямоугольным треугольником.
Самая длинная сторона называется гипотенузой, а две другие стороны могут быть равны или не равны друг другу. Прямоугольный треугольник, у которого две стороны равны, называется равнобедренным прямоугольным треугольником.
Как найти недостающую сторону прямоугольного треугольника?
Недостающую сторону прямоугольного треугольника можно найти, если известна мера двух других сторон. Теорема Пифагора помогает найти значение недостающей стороны. По теореме Пифагора квадрат гипотенузы равен сумме квадратов двух других сторон прямоугольного треугольника. Например, если а, b и с — три стороны прямоугольного треугольника, где «а» — гипотенуза, то, согласно теореме, a 2 = б 2 + в 2 .
Как найти угол прямоугольного треугольника?
Расчет углов прямоугольного треугольника очень прост. Один из углов прямоугольного треугольника является прямым углом или 90 º . Теперь, если известен другой угол треугольника, то недостающий угол можно легко вычислить, используя свойство суммы углов, которое утверждает, что сумма углов треугольника всегда равна 180º.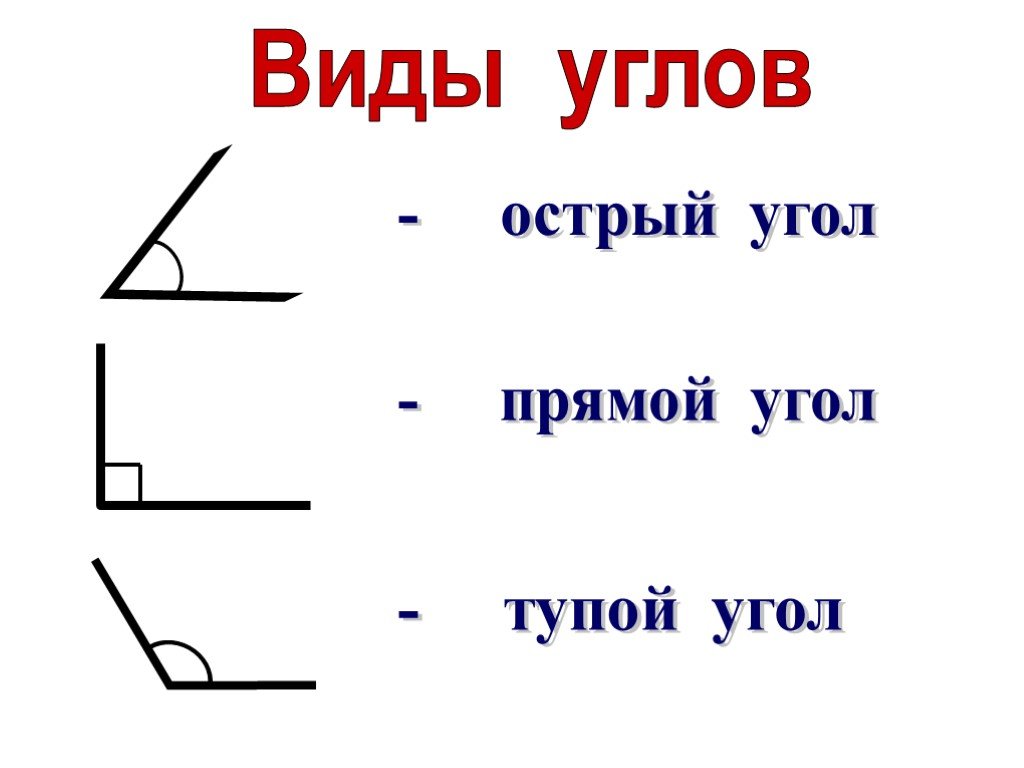

 е.
е.
 Подставляя b = 12 единиц и h = 5 единиц, мы имеем Площадь = 1/2 × 12 × 5 = 30 единиц 2 . Следовательно, площадь прямоугольного треугольника равна 30 квадратных единиц.
Подставляя b = 12 единиц и h = 5 единиц, мы имеем Площадь = 1/2 × 12 × 5 = 30 единиц 2 . Следовательно, площадь прямоугольного треугольника равна 30 квадратных единиц.