Как определить угол 90 градусов на плоскости: Как вычислить угол 90 градусов в строительстве

как обозначить и измерить углы, правила

Определение

Геометрия — это раздел математики, который занимается изучением форм и их измерений. Он также фокусируется на относительной конфигурации форм и их пространственных свойствах.

Все геометрические фигуры состоят из точек, линий, лучей и плоской поверхности. Когда две линии или лучи сходятся в одной точке, измерение между двумя линиями называется углом. В этой статье мы собираемся обсудить, что такое угол, каковы различные типы углов и их значение с примерами.

Определение угла в математике

Определение

Что такое угол? Угол это — геометрическая фигура, образованная двумя лучами или линиями, имеющими общую конечную точку (вершину). Два луча называются сторонами угла, а точка, в которой пересекаются лучи, называется вершиной.

Угол, лежащий в плоскости, не обязательно должен лежать в евклидовом пространстве. В случае, если углы образованы пересечением двух плоскостей в евклидовом или другом пространстве, такие углы считаются двугранными.

Стороны угла – лучи, которые образуют угол (А, В).

Вершина угла – точка, из которой выходят лучи (О).

Угол делит плоскость на две части. Если угол не развернутый, то одна часть плоскости называется областью внутреннего угла, а другая часть называется областью внешнего угла. Ниже приведена картинка, поясняющая, какие части являются внешними, а какие внутренними.

Если углы измеряются по линии, мы можем найти два разных типа углов, например, положительный угол и отрицательный угол.

• Положительный угол: если угол идет против часовой стрелки, то он называется положительным углом.
• Отрицательный угол: если угол направлен по часовой стрелке, то он называется отрицательным углом.

Интересно

Слово «угол» произошло от латинского слова Angulus, означающего «небольшой изгиб».

Понятие угла впервые использовал Евдем, который определил угол как отклонение от прямой линии.

Как обозначить углы?

Фигура угол отмечается символом «∠». Есть два разных способа обозначения углов:

• Способ 1:
  Как правило, угол обозначается строчными буквами, такими как «а», «х» и т. д., или греческими буквами альфа (α), бета (β), тэта (θ) и т. д.
• Способ 2:
  Используя три буквы на фигурах. Средняя буква должна быть вершиной (фактический угол).
  Например, ABC — треугольник. Чтобы представить угол A равным 60 градусам, мы можем определить его как ∠BAC = 60 °.

Типы углов

Существует шесть типов углов. Каждый тип угла имеет уникальную идентификацию на основе измерения угла.
Давайте прочитаем о каждом типе угла в отдельности вместе с их свойствами.

1. Острый угол – это угол, градусная мера которого больше 0° и меньше 90°.
2. Прямой угол — когда измерение угла равно 90 градусов, он известен как прямой угол.
   Прямой угол можно легко наблюдать, так как он образует форму буквы L.
3. Тупой угол — когда измерение угла меньше 180 градусов, но больше 90 градусов,
   это тупой угол.
4. Развернутый угол — угол, образованный прямой линией, называется прямым углом. Это
   половина полного оборота круга. Размер прямого угла равен 180°.
5. Выпуклый угол – это угол, величина которого больше 180°, но меньше 360°.
6. Полный угол — когда измерение угла равно 360 градусам, это полный угол.

Ряд углов образуется при пересечении секущей двух или более прямых. Конкретные названия даны паре углов, что зависит от расположения угла по отношению к прямым. Линии могут быть как параллельными, так и непараллельными.

Углы образованные при пересечении двух прямых

При пересечении двух прямых образуются два вида углов:

• смежные;
• вертикальные.

Смежные углы

Определение

Два угла называются смежными, если они имеют общую вершину и одну общую сторону, а две другие стороны расположены на одной прямой и образуют развернутый угол. Смежные углы между собой дополняемые, так как являются продолжением один другого.

Свойства смежных углов

1. Сумма смежных углов равна 180°
2. Если оба смежных угла равны между собой, то они являются прямыми.
3. В паре смежных углов всегда один острый, а другой тупой, или оба угла прямые.
4. Синусы смежных углов равны.
5. Косинусы, тангенсы и котангенсы смежных углов равны, но имеют противоположный знак.

Вертикальные углы

Определение

Вертикальные углы – пара углов, у которых стороны одного угла являются продолжением сторон второго.

Свойство: вертикальные углы равны.

Пример:

Пары углов 1 и 3; 2 и 4 – являются вертикальными

По свойству вертикальных углов:

\[\angle C O D=\angle A O B\]

\[\angle B O D=\angle A O C\]

Пары углов 1 и 2, 2 и 3, 3 и 4, 4 и 1 — являются смежными

По свойству смежных углов:

\[\angle C O D+\angle D O B=180^{\circ}\]

\[\angle D O B+\angle B O A=180^{\circ}\]

\[\angle B O A+\angle A O C=180^{\circ}\]

\[\angle A O C+\angle C O D=180^{\circ}\]

Смежные углы	Вертикальные углы
Два угла с общей стороной и вершиной называются смежными.	Когда две прямые пересекаются друг с другом, то пары противоположных углов, образованных при вершине, называются вертикальными углами.
Имеют общую сторону и общую вершину.	Имеют общую вершину, но не имеют общую сторону
Смежные углы не всегда равны по величине	Вертикально противоположные углы равны по величине

Разница между смежными и вертикальными углами

Сравнение углов

Для сравнения углов можно использовать простейший метод — метод наложения. Для этого нужно совместить две вершины и сторону одного угла со стороной другого. Если стороны данных углов совпадают, то углы равны. В противном случае угол, который находится внутри другого, будет меньше. Вот два наглядных примера с равными и неравными углами:

\[\angle A_{1} O_{1} B_{1}\] и \[\angle A_{2} O_{2} B_{2}\] полностью совмещаются при наложении следовательно: \[\angle A_{1} O_{1} B_{1}=\angle A_{2} O_{2} B_{2}\]

\[\angle A_{1} O_{1} B_{1}\] и \[ \angle A_{2} O_{2} B_{2}\] не совмещаются при наложении: \[\angle A_{1} O_{1} B_{1} \neq \angle A_{2} O_{2} B_{2}\]

Причем: \[\angle A_{1} O_{1} B_{1}<\angle A_{2} O_{2} B_{2}\]

При этом развернутые углы всегда являются равными.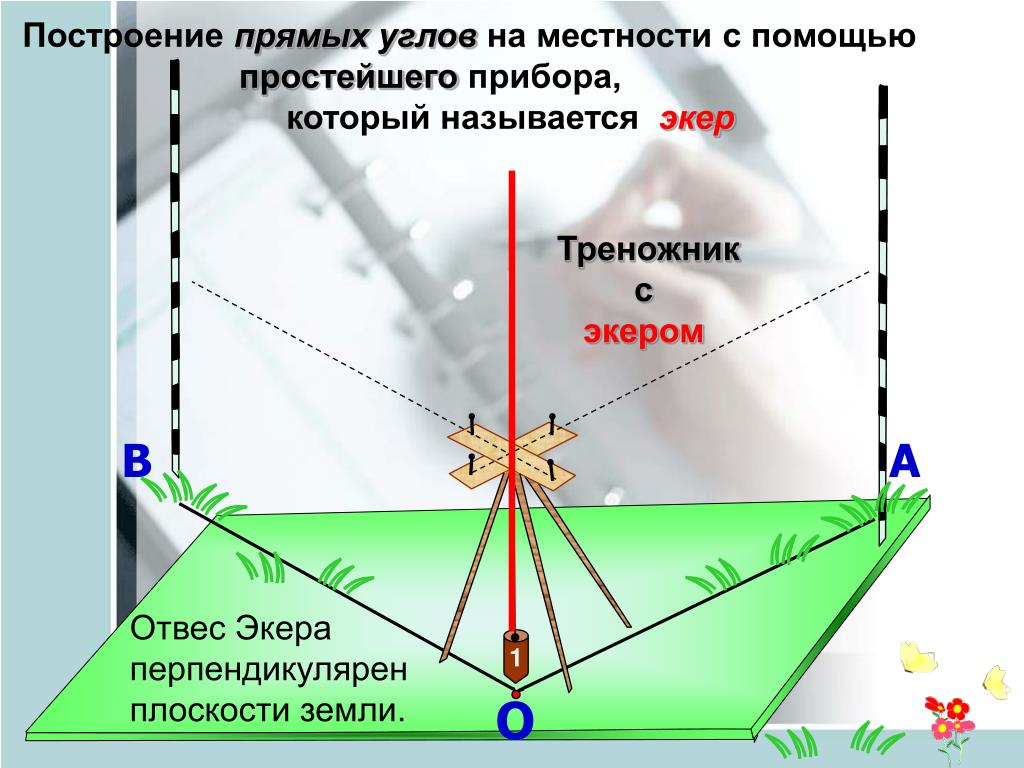

Совмещение углов \[\angle A B C\] и \[\angle M N K\] происходит следующим образом:

1. Вершину B одного угла совмещаем с вершиной N другого угла.
2. Сторону BA одного угла накладываем на сторону NM другого угла так, чтобы стороны BC и NK располагались в одном направлении.

Если совпадут и другие стороны, то углы равны: ∠ABC = ∠MNK.

Если нет, то один угол — меньше другого: ∠ABC<∠MNK.

Некоторые важные теоремы, основанные на прямых и углах:

1. Если две параллельные прямые пересечены секущей, то смежные внутренние углы имеют одинаковую величину.
2. Если две параллельные прямые пересечены секущей, то противоположные внешние углы имеют одинаковую величину.
3. Если две параллельные прямые пересечены секущей, то соответствующие углы имеют одинаковую величину.
4. Если две параллельные прямые пересечены секущей, то внутренние углы по одну сторону от этой секущей смежные.
5. Вертикальные углы равны, когда прямая пересекает прямые. Линии могут быть как параллельными, так и непараллельными.

Измерение углов

Существует несколько единиц измерения углов. Рассмотрим наиболее часто используемые единицы измерения:

Градусная мера

Полный оборот, т. е. когда начальная и конечная стороны находятся в одном и том же положении после вращения по часовой стрелке или против часовой стрелки, делится на 360 единиц, называемых градусами. Итак, если поворот от начальной стороны к конечной стороне составляет \[\left(\frac{1}{360}\right)\] оборота, то говорят, что угол имеет меру в один градус. Обозначается как 1°.

Мы измеряем время в часах, минутах и ​​секундах, где 1 час = 60 минут, а 1 минута = 60 секунд. Точно так же при измерении углов

• 1 градус = 60 минут, обозначаемый как 1° = 60′.
• 1 минута = 60 секунд, обозначаемая как 1 ′ = 60 ″.

Несколько примеров углов с их измерениями

Радианная мера

Радианная мера немного сложнее, чем градусная. Представьте круг с радиусом 1 единица. Далее представьте дугу окружности длиной 1 единицу. Угол, образуемый этой дугой в центре окружности, имеет меру 1 радиан. Вот как это выглядит:

Вот еще несколько примеров углов: -1 радиан, радиан, \[1 \frac{1}{2}\] радиан, \[-1 \frac{1}{2}\] радиан.

Длина окружности = \[2 \pi r \ldots\] где r — радиус окружности. Следовательно, для круга с радиусом 1 единица длины окружности равна \[2 \pi\]. Следовательно, один полный оборот начальной стороны образует в центре угол \[2 \pi\] радиан. Обобщая это, имеем:

В окружности радиуса r дуга длины r образует угол в 1 радиан в центре. Следовательно, в окружности радиуса r дуга длины l будет опираться на угол = \[\frac{l}{r}\] радиан. Обобщая это, мы имеем в окружности радиуса r, если дуга длины l образует угол θ радиан в центре, то:

\[\theta=\frac{l}{r}\]

\[l=r \theta\]

Связь между степенью и радианными мерами

По определениям степени и радиана мы знаем, что угол, образуемый окружностью в центре, равен:

• 360° – по градусной мере
• \[2 \pi\] радиан — в радианах

Следовательно, \[2 \pi\] радиан = 360° ⇒ \[\pi\] радиан = 180°. {\prime}=\frac{\pi}{180} \times \frac{121}{3}=\frac{121 \pi}{540}\] радиан.

Нет времени решать самому?

Наши эксперты помогут!

Контрольная

| от 300 ₽ |

Реферат

| от 500 ₽ |

Курсовая

| от 1 000 ₽ |

Как измерить угол

Для измерения углов используется транспортир:

Транспортир

Попробуем измерить угол \[\angle A O B\]

Шаги для измерения угла \[\angle \mathrm{AOB}\].

Шаг 1: совместите транспортир с лучом OB, как показано ниже. Начните чтение с отметки 0 ° в правом нижнем углу транспортира.

Шаг 2: Число на транспортире, совпадающее со вторым лучом, является мерой угла. Измерьте угол, используя число на «нижней дуге» транспортира. Таким образом, ∠ AOB = 37°

Далее попробуем измерить этот ∠AOC:

Шаг 1: Измерьте угол от отметки 0° в левом нижнем углу.

Шаг 2: Число на «верхней дуге» транспортира, совпадающее с OA, является мерой ∠ AOC. Таким образом, ∠ AOC = 143°

Как построить углы

Используем транспортир для построения углов. Нарисуем угол 50°.

Шаг 1: сначала нарисуйте луч OB и совместите транспортир с OB, как показано.

Шаг 2: поместите точку над отметкой на транспортире, которая соответствует 50°.

Шаг 3: Уберите транспортир и нарисуйте луч, начинающийся в точке О и проходящий через эту точку. Таким образом, ∠AOB – искомый угол, т.е. ∠AOB = 50°.

Примечание. Если луч идет в другом направлении, мы измеряем угол от отметки 0° в левом нижнем углу.

На изображении ниже показано, как нарисовать угол 50°, когда луч указывает в другом направлении.

Обозначение углов на чертеже

Для комфортного отображения дуг, углов применяют чертежи. Не всегда возможно грамотно изобразить и обозначить тот или другой угол, дугу или наименование. Равные углы имеют определение в виде идентичного числа дуг, а неравноценные в виде различного.

На чертеже запечатлено корректное обозначение острых, равных и неравных углов.

Если нужно обозначить более трех углов, то применяются специальные обозначения дуг, например, зубчатые или волнистые, но в принципе это не имеет особого значения.

Обозначение углов должно быть простым, чтобы не препятствовать иным значениям. При решении задачи рекомендовано обозначать только нужные для решения углы, чтобы не перегружать весь чертеж. Это не помешает решению задачи, а также придаст эстетичный облик чертежу.

Обозначение угла на чертеже – как указать в градусах и размеры / виды / диаметр

Углы – это геометрические фигуры, образованные двумя лучами, которые выходят из одной точки. Обозначения углов регламентированы ГОСТ 2.307-2011 «Нанесение размеров и предельных отклонений».

Как обозначается угол на чертеже

Угол на чертеже обозначается с помощью универсального и общепринятого символа, на котором показаны два луча, выходящие из одной точки. За символом указывается размер угла в градусах, минутах и секундах. Острый угол символа направлен в сторону уклона.

Обозначение углов на чертеже по ГОСТу

Согласно ГОСТ 2.307 размеры делятся на линейные и угловые. И если в линейных размерах не ставят единицы измерения, т. к. всегда подразумевается, что значения приведены в миллиметрах, то для угловых размеров обязательно указывается значок градуса, минуты и секунды, в зависимости от того, в каких величинах измеряется угол.

Рисунок 1. Линейные и угловые размеры

Как показать угол на чертеже

Чтобы показать размер используются сплошные тонкие линии, они могут быть выносные или размерные. Любой угол имеет вершину и две стороны. Градусами или минутами обычно обозначается внутренняя сторона угла. В качестве условного обозначения используется символ в виде острого угла, далее указывается числовое значение и единицы измерения. Следует помнить о том, что минута — это одна шестидесятая часть градуса, а секунда одна шестидесятая часть минуты. Градусы обозначаются с помощью маленького круга в верхнем правом углу возле значения, минуты обозначаются одной надстрочной запятой, а секунды двумя надстрочными запятыми.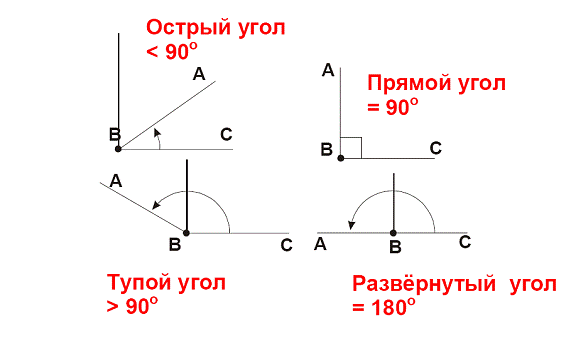

Допуск угла

В ГОСТ 8908-81 приведены стандарты на допуски углов, применяемые в машиностроении, при меньшей стороне угла до 2,5 м. Значения уклона и угла уклона приведены в таблице (рис. 1). Стандартом установлено 17 степеней точности допусков, которые зависят от длин сторон и размера угла.

Рисунок 2. Степень точности допуска угла

Виды углов на чертеже

На чертежах могут быть обозначены следующие виды углов:

• острый – менее 90 градусов;
• прямой — равен 90 градусам;
• тупой — более 90 и менее 180 градусов;
• развернутый — равен 180 градусам.

Обозначение у прямого и развернутого угла ставится при необходимости.

Углы наклона

Угол уклона часто встречается как на машиностроительных, так и на строительных чертежах. Он показывает, под каким углом к базовой линии расположен наклонный элемент. Для обозначения наклона используется универсальный символ, который ставится перед размерным числом.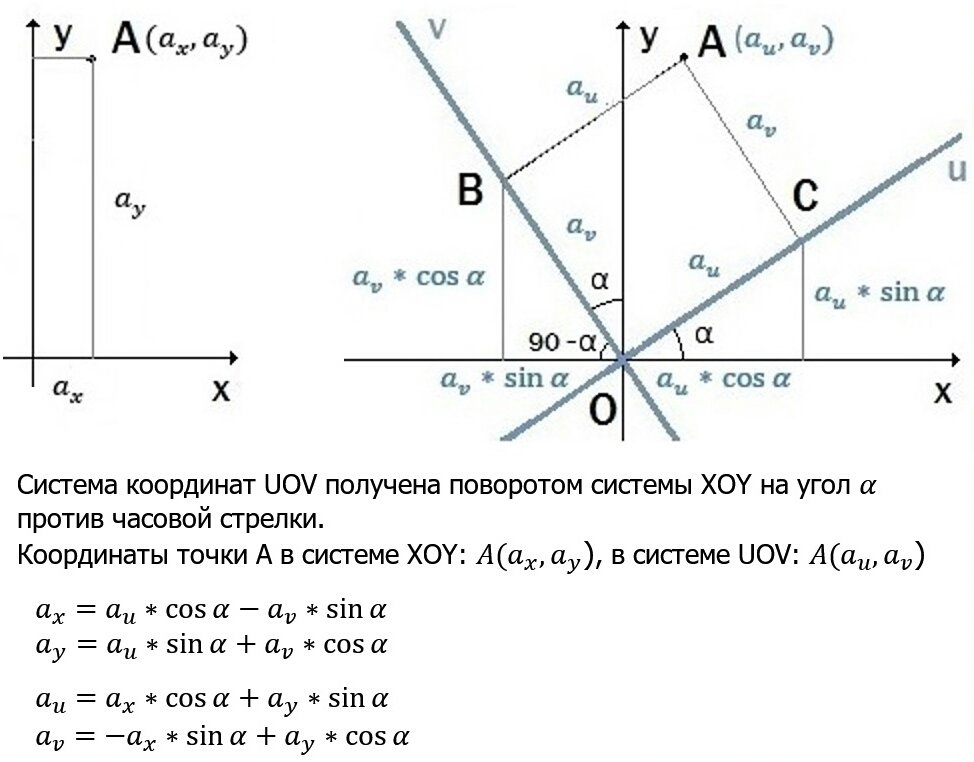 К примеру, на строительном чертеже отмостка всегда имеет уклон, для обозначения этого уклона ставится символ и значение в 5 промилле.

Рисунок 3. Обозначение уклона на плане кровли

Промилле — это одна тысячная или десятая часть процента, поэтому к знаку промилле добавлен еще один нолик. Через промилле в строительных чертежах указывается уклон пандусов и других наклонных поверхностей.

Рисунок 4. Уклон на чертеже

Рисунок 5. На узле сопряжения сендвич панелей указывается угол под которым конструкции крпятся друг к другу

Рисунок 6. Углы. На строительном чертеже обозначен угол в 33 градуса

Угол преломления

Преломление возникает на границе двух сред, при этом угол падения равен углу отражения. Падающий и отраженный лучи показывают на чертеже, а значение угла наносят относительно вертикали, прямого угла.

Рисунок 7. Угол преломления

Вертикальные углы

Согласно определению вертикальными называют два угла, в том случае, если стороны одного угла являются продолжением сторон другого. Такие углы будут попарно равны. Обычно на чертеже их обозначают с помощью полукруга или двойного полукруга.

Рисунок 8. Вертикальные углы, пример обозначения

Многогранные углы

Понятие многогранного угла относится к трехмерному пространству, такой угол состоит из плоских углов, которые его образуют, имея общую точку. При этом они не должны лежать в одной плоскости.

У многогранного угла есть два свойства:

• сумма плоских углов многогранного угла превышает 360 градусов;
• существует плоскость, пересекающая все ребра многогранного угла.

По количеству граней многогранные углы делят на трехгранные, четырехгранные, пятигранные и так далее.

Самым показательным примером многогранного угла является вершина четырехугольной пирамида. Многогранный угол может быть невыпуклым и выпуклым.

Смежные углы

Смежными называются углы, которые имеют одну общую сторону, а две другие их стороны являются продолжением друг друга. Сумма смежных углов равна 180 градусам. Поэтому, если известно значение одного угла, то найти значение второго не составляет труда.

Рисунок 9. Пример смежных углов

Углы фаски

Деталь может иметь скос или скругление, которое называется фаской. Обозначение фаски установлено в ГОСТ 2.307-2011, обычно ее показывают размерными линиями. Запрещено использовать осевые и контурные линии для обозначения фаски. На чертеже обязательно указывают ширину, размер скоса и угол относительно главной оси элемента или механизма. Если на чертеже показана фаска, но не указан угол, то подразумевается ее стандартное значение 45 градусов. Обозначение выполняется с помощью выносной линии или с помощью линейных размеров.

Рисунок 10. Обозначение фаски по ГОСТ

Внешние углы на чертеже

На чертежах может потребоваться указать внешний угол треугольника, это угол смежный с любым из внутренних углов. Следовательно, у каждой вершины можно построить два равных внешних угла. Также существует теорема, доказывающая что внешний угол равен сумме двух внутренних углов, которые не смежны с ним.

Центральные углы на чертеже

Центральным называется угол, который равен градусной мере дуги, на которую он опирается. Центральный угол отличается от вписанного тем, что вершин вписанного угла лежит на окружности, и он равен половине дуги, на которую опирается. Вписанные и центральные углы имеют зависимость, например, если нарисовать их на одной окружности, то вписанный угол будет равен половине центрального, если они опираются на одну дугу. Таким образом, зная один угол, можно определить другой.

Ответы на вопросы

Как обозначается радиус окружности на чертеже?

Для обозначения радиуса используется значок R, после которого указывается значение в миллиметрах и сплошная тонкая линия со стрелкой на конце. Радиус проводят от центра окружности к обозначаемому отрезку. Обычно указывают только радиус, диаметр при необходимости можно найти путем удвоения радиуса.

Как указать прямой угол?

При обозначении острого или тупого угла в основании между лучами проводят полукруг, если угол прямой в его основании рисуют квадрат.

Как отсчитывают угол на чертеже?

Угол образовывается двумя лучами, чтобы найти его значение используют транспортир.

Что такое плоская геометрия? Определение, типы, примеры, факты

Что такое плоская геометрия?

Планиметрия имеет дело с плоскими фигурами, которые можно нарисовать на листе бумаги, такими как квадраты, круги и треугольники. Объемная геометрия имеет дело с трехмерными твердыми формами, которые существуют вокруг нас, такими как сферы, конусы и кубы.

Предположим, вам нужно нарисовать Землю на листе бумаги. Как бы Вы это сделали? Простым способом было бы нарисовать круг, чтобы представить планету. Земля, которую вы нарисуете, будет иметь плоскую форму. Но Земля, на которой мы живем, не является плоским объектом. Он имеет сферическую форму.

Раздел математики, изучающий формы, размеры, размеры и углы объектов, известен как геометрия. Он широко делится на два типа: плоскостная геометрия и объемная геометрия.

Сегодня мы рассмотрим определение планиметрии и многое другое. Давайте погрузимся прямо сейчас!

Родственные игры

Как определить плоскость в геометрии?

В геометрии плоскость — это плоская поверхность, имеющая два измерения. Он простирается бесконечно и не имеет толщины. Вы можете думать о листе бумаги или поверхности стены как о части геометрической плоскости.

Плоские формы в планиметрии известны как плоские фигуры. Мы можем измерить их по длине и высоте или по длине и ширине. Но в них нет глубины.

Некоторыми распространенными примерами плоских фигур являются линии, прямоугольники, круги и треугольники.

Связанные рабочие листы

Основные термины в планиметрии

Когда дело доходит до планиметрии, нам необходимо знать несколько терминов, таких как:

• Точка
• Строка

Что такое точка?

Точка обозначает точное положение на плоскости.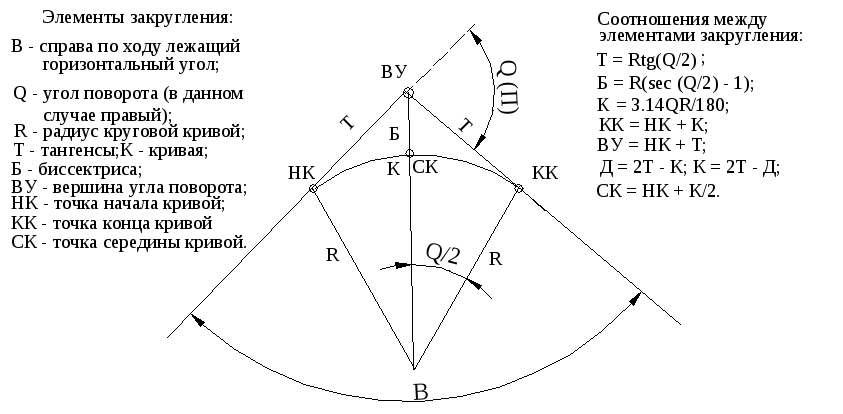 Он дает нам позицию, но не имеет измерения.

Обычно для обозначения точки используется точка. Точка часто имеет имя, например «A», «B», «C» и т. д.

Что такое линия?

Линия — это одномерная прямая фигура. Он формируется, когда объединяются бесчисленные точки. Он не имеет толщины и безгранично простирается в обоих направлениях. Мы не можем измерить его длину. Линия представлена ​​двумя стрелками на каждом конце, чтобы указать, что она простирается бесконечно в обоих направлениях.

Возможно, вы уже встречали термины «отрезок прямой» и «луч». Они оба являются частями линии.

Сегмент линии: сегмент линии имеет две определенные конечные точки. Мы можем измерить его длину. Примером отрезка является край листа бумаги. Отрезок линии представлен линией без стрелок на концах.

Луч: Луч имеет определенную начальную точку, но не имеет конечной точки и может бесконечно продолжаться в одном направлении. Мы не можем измерить его длину. Луч представлен линией с единственной стрелкой на одном конце, указывающей, что он простирается бесконечно в одном направлении. Примером луча является солнечный луч.

Забавный факт: греческий математик Евклид определил линию как «длину без ширины».

Углы в плоской геометрии

Что общего между краем стола, наконечником стрелки и куском пиццы? Все они являются примерами углов, которые мы видим вокруг себя.

Угол образуется, когда два луча встречаются в конечной точке. Лучи — это стороны угла, а их общий конец — вершина.

Углы измеряются в градусах (°).

Типы уголков

Острый угол: Острый угол (или острый угол) измеряется между 0° и 90°.

Прямой угол: Прямой угол равен 90°.

Тупой угол: Тупой угол имеет размеры от 90° до 180°.

Прямой угол: Прямой угол равен 180°.

Угол рефлекса: Угол рефлекса составляет от 180° до 360°.

Полный угол: полный угол равен 360°.

Примеры плоской геометрии

Многоугольник

Многоугольник представляет собой замкнутую форму, образованную сегментами прямых линий. Это двумерная фигура с конечным числом сторон.

Стороны образуют ребра многоугольника. Место встречи двух сторон называется вершиной.

Имя многоугольника зависит от количества его сторон. Обычно его обозначают n-угольником, где n — количество сторон. Каждый многоугольник имеет 3 или более сторон.

Примерами многоугольников являются треугольники, квадраты и прямоугольники.

Круг в геометрии

Круг — это замкнутая круглая фигура без краев и углов. Это двумерная изогнутая форма.

Слово «круг» происходит от греческого слова kirkos , что означает кольцо или обруч.

Расстояния между центром круга и каждой точкой круга одинаковы. Это расстояние является радиусом окружности.

Забавный факт: Flatland — это вымышленная история Эдвина Эбботта, в которой он рассуждает о том, каково было бы жить в двухмерном мире (на плоскости). Подумайте немного о том, какие изменения это принесет в ваш мир, если такое произойдет!

Заключение

Знание планиметрии необходимо для измерения линий, углов и поверхностей. Он закладывает основу для изучения объемной геометрии.

Решенные примеры

Пример 1: Фигура под линией или отрезком?

Решение : Данная фигура является линией. Несмотря на то, что он имеет две определенные точки А и В, две стрелки указывают на то, что он бесконечно простирается в обоих направлениях. Это показывает, что это линия.

Пример 2: Какая из следующих фигур не является многоугольником?

Решение : Рис. d не является многоугольником. Это изогнутая форма, а многоугольники образованы отрезками прямых линий.

Пример 3: Определите тупые углы в следующем пересечении прямых.

Пересечение прямых Решение : Здесь ∠CDE и ∠GDH — два тупых угла. Они больше 90°, но меньше 180°.

Практические задачи

1

Какое из утверждений неверно?

Геометрическая плоскость представляет собой двумерную поверхность.

Геометрическая плоскость простирается бесконечно.

Геометрическая плоскость имеет толщину.

Линия является примером плоской фигуры.

Правильный ответ: Геометрическая плоскость имеет толщину.
В геометрии плоскость не имеет толщины.

2

Сколько измерений имеет точка?

Три

Один

Два

Ноль

Правильный ответ: Ноль
Точка не имеет измерения.

3

Что из перечисленного является рефлекторным углом?

45°

265°

180°

110°

Правильный ответ: 265°
Углы рефлекса измеряются между 180° и 360°.

Часто задаваемые вопросы

Все ли двумерные фигуры являются полигонами?

Нет, все 2D-фигуры не являются полигонами. Например, круг — это двумерная фигура, но не многоугольник.

Сколько точек может составить плоскость?

Любые три точки, не лежащие на одной прямой, могут составить плоскость.

Что такое правильный многоугольник?

Правильный многоугольник имеет равные стороны и углы.

Перпендикулярность | Основы GD&T

Перпендикулярность поверхности:

Перпендикулярность оси :

Описание:

Поверхность:

Перпендикулярность — довольно распространенный символ, который требует, чтобы указанная поверхность или линия были перпендикулярны или 90° от базовой поверхности или линии. Перпендикулярность может относиться к 2D-линии, но чаще она описывает ориентацию одной плоскости поверхности, перпендикулярной другой базовой плоскости. Допуск условного обозначения перпендикулярности косвенно управляет углом 90° между деталями, контролируя положение, в котором должны лежать поверхности. См. зону допуска ниже для более подробной информации.

Примечание. Перпендикулярность не влияет на угол ссылочного элемента — допуск выражается в единицах расстояния. (мм/дюйм)

Ось:

Управление осью также может быть вызвано для Перпендикулярности и является одной из наиболее распространенных форм вызова осей. Когда на него ссылаются для круглого элемента, рамка управления элементом будет содержать символ диаметра (Ø). Перпендикулярность оси может быть применена к положительному элементу (штифт/выступ) или к отрицательному элементу (отверстию). Когда Перпендикулярность используется для осевого управления элементом, символ теперь задает цилиндрическую границу, где должна лежать ось указанного элемента. Эта цилиндрическая граница формируется путем взятия линии, которая перпендикулярна базовому элементу. Когда вызывается эта версия перпендикулярности, она должна использоваться с максимальным состоянием материала, чтобы облегчить измерение детали. См. пример 2 ниже, чтобы узнать, как измеряются эти конкретные детали.

Зона допуска GD&T:

Поверхность:

Две параллельные плоскости или линии, ориентированные перпендикулярно базовому элементу или поверхности. Плоскости удерживаются перпендикулярно к базе, но только для того, чтобы весь элемент попал в зону допуска.

Помните: Перпендикулярность напрямую не управляет углом поверхности, на которую ссылаются; он контролирует оболочку (например, плоскостность), где должна быть поверхность.

Ось:

Цилиндр, окружающий заданную теоретическую ось, которая перпендикулярна опорному элементу. Зона допуска — это диаметр этого символа, в котором должна лежать центральная ось измеряемого элемента.

Калибровка/Измерение:

Поверхность:

Перпендикулярность измеряется с помощью штангенциркуля, аналогично плоскостности, 90°, чтобы измерить, насколько перпендикулярна поверхность. Вся поверхность должна быть измерена, если это плоский элемент.

Ось:

Чтобы гарантировать, что деталь или элемент аксиально перпендикулярны, максимальное состояние материала чаще всего вызывается для перпендикулярности оси, чтобы облегчить измерение с помощью калибра. Это позволяет проектировать его как для отрицательного (отверстие), так и для положительного (штифт) элемента и может учитывать дополнительный допуск.*

Размер датчика для внутреннего элемента (например, отверстия):

Калибр Ø (штифт) = Мин. Ø отверстия (MMC) – Допуск перпендикулярности

Размер калибра для внешнего элемента (например, штифта):

Калибр Ø (калибра) = Макс. Ø штифта (MMC) + Допуск перпендикулярности

См. Пример № 2 ниже для хорошего примера перпендикулярности оси с использованием MMC.

*Примечание к дополнительному допуску:

Когда для перпендикулярности используется функциональный калибр, любое отличие фактического размера элемента от максимального состояния материала будет дополнительным допуском. Цель обозначения максимального состояния материала состоит в том, чтобы гарантировать, что, когда деталь находится в наихудших допусках, ориентация 9Размер отверстия/штифта 0093 и всегда будет собираться вместе. Это означает, что если вы сделаете булавку меньше, вы получите больше бонусной терпимости для себя. Этот бонус можно добавить к допуску GD&T, что расширит допуск перпендикулярности.

Бонусный допуск = разница между MMC и фактическим состоянием (см. пример 2 ниже)

Еще не запутались? Не беспокойся! Дополнительные сведения см. в разделах «Максимальное состояние материала».

Связь с другими символами GD&T:

Поверхность:

Перпендикулярность — это особая форма угловатости под углом 90°. Все символы ориентации (Угловатость, Параллельность и Перпендикулярность) вызывают конкретную оболочку элемента, связанную с базой.

Перпендикулярный символ также тесно связан с плоскостностью, когда базовая/измеренная поверхность является плоскостью поверхности. Когда вы вызываете Перпендикулярность, подразумевается плоскостность (вы измеряете изменение поверхности между двумя параллельными плоскостями = Плоскостность). Перпендикулярность всегда измеряется относительно базы, а плоскостность — нет.

Ось:

Перпендикулярность тесно связана со всеми другими символами GD&T ориентации при вызове на оси. Зона допуска теперь относится к однородности и цилиндрической оболочке центральной оси. Перпендикулярность и параллелизм можно вызвать на отверстиях и цилиндрических штифтах, часто с добавлением MMC.

При использовании:

Поверхность:

Всякий раз, когда две поверхности нуждаются в постоянном угле 90°, Перпендикулярность эффективна. Фланцевые подшипники и критические квадратные кромки обычно ссылаются на него. Перпендикулярность также обычно указывается на углах цилиндров, где плоское дно должно быть перпендикулярно изогнутым сторонам.

Ось:

Перпендикулярность очень часто обозначается на центральной оси отверстия. Почти всегда ваше отверстие должно быть перпендикулярно поверхности, в которой оно просверлено. В этом случае она вызывается вместе с MMC, чтобы гарантировать, что, если штифт или болт необходимо вставить в это отверстие, деталь может войти во весь перпендикуляр и всегда будет входить. См. пример 2 для этого объяснения.

Перпендикулярность поверхности Пример:

Край стопорного блока для рельса должен образовывать 90°, чтобы обеспечить надлежащий стыковочный контакт. Основание блока будет нашей базой, а грань, где стопорный блок соприкасается, будет нашей опорной поверхностью. Чтобы гарантировать, что эта грань всегда будет перпендикулярна и плоской, чтобы обеспечить хороший контакт, вам необходимо строго контролировать угол и размерную ширину детали.

Обеспечение перпендикулярных/плоских поверхностей без символа GD&T

С помощью перпендикулярности вы можете открыть размер ширины и очень точно контролировать угол грани, содержащей деталь. Ваша зона допуска остается прежней, но теперь вашу деталь легче контролировать и изготавливать.

Контроль перпендикулярности с помощью символа GD&T.

Перпендикулярность оси Пример с MMC:

Если у вас есть важный элемент отверстия, который должен оставаться параллельным формируемой поверхности, можно вызвать перпендикулярность, чтобы гарантировать прямолинейность отверстия. В этом примере отверстие под болт остается перпендикулярным его поверхности.

Перпендикулярность на отверстии под ММС

Без обозначения MMC вам нужно было бы контролировать только центральную ось отверстия и измерять ее, чтобы убедиться, что она находится под углом 90° к нижней поверхности. Однако, когда MMC вызывается на отпечатке, вы контролируете как размер, так и ориентацию отверстия. Теперь вы можете проверить оба допуска с помощью функционального калибра со следующими размерами:

Формула для функционального калибра перпендикулярности:

Калибр Ø (штифтовой калибр) = Мин. Ø отверстия – Допуск перпендикулярности

Калибр Ø = 90,9 – 0,2 = 9,7

Ø отверстия + Перпендикулярность отверстия > 9,7 (Ø штифта) в спецификации.

Из-за сноски Max Material Condition, если у вас есть отверстие больше, чем MMC 9,9, у вас будет дополнительный допуск, который можно добавить к вашей перпендикулярности. (Согласно печати Ø отверстия не может быть больше 10,1)

В приведенном ниже примере — отверстие находится в минимальном состоянии материала (наибольший размер отверстия) с отверстием в LMC, ваш бонусный допуск, который можно добавить к перпендикулярности, равен рассчитывается следующим образом:

Бонусный допуск = фактический размер детали – максимальное состояние материала часть находится в наибольшем диаметре.