Как определить угол наклона: Как рассчитать угол наклона крыши

Угол наклона рельефа на местности: как измерить

Те пользователи, которые работают с рельефом в программе Наш Сад и используют для этого редактор Рельефа, знают: чтобы наклонить поверхность нужно задать угол ее наклона в градусах. Как же определить угол наклона рельефа подручными средствами, если в «кустах», случайно нет теодолита или тахеометра?

Метод вешек

Нам понадобятся: 3 колышка, шнур, рейка жесткая, уровень.
Вбиваем две вешки (колышка) по краям на перепаде высот (см. схему). Забиваем гвоздь или вкручиваем шуруп в произвольной точке С одной из вешек. Замеряем расстояние d от поверхности земли. Привязываем в этом месте шнур и с натяжением закрепляем его к другой вешке в точке А на том же, одинаковом расстоянии d от земли. Берем жесткую рейку, такую, чтобы не прогибалась и закрепляем на ней уровень. Устанавливаем рейку так, чтобы один ее конец находился в точке С, а другой лежал на еще одной вешке. Эту вешку забиваем в землю таким образом, чтобы она касалась натянутого шнура. Рейка на ней должна лежать горизонтально по уровню. Измеряем расстояние DE от шнура до рейки по вертикали и расстояние DС по горизонтали. Согласно схеме это длина рейки. Нам нужно найти значение угла β в градусах. Это и будет искомый угол наклона.

Мы легко можем измерить и вычислить соотношение DE/DC. В тригонометрии это тангенс угла — число, которое определяется соотношением противолежащего и прилежащего к этому углу катетов треугольника CDE. Зная это соотношение можно вычислить величину угла, например, воспользовавшись тригонометрической функцией, обратной тангенсу — арктангенсом.

Вычисляем угол наклона на калькуляторе Windows

Значение арктангенса вычисляем, используя стандартный калькулятор из состава Windows. Щелкаем кнопку «Пуск», переходим в раздел «Все программы», находим «Стандартные» и жмем «Калькулятор». Этот же результат достигнем, нажав сочетание клавиш WIN + R, набрав в строке «Выполнить» команду calc и щелкнув кнопку «OK».
Переключаем калькулятор в режим вычисления тригонометрических функций. Для этого открываем меню «Вид» и находим пункт «Инженерный» или «Научный» (в зависимости от версии используемой операционной системы).
Вводим известное значение тангенса. Это делаем с клавиатуры или щелкая нужные кнопки интерфейса калькулятора.
При этом выбираем единицу измерения «Градусы» — DEG, чтобы получить результат вычисления именно в градусах, а не в радианах или градах. Ставим метку в checkbox (пустом квадратике) с надписью Inv. Так инвертируем значения вычисляемых функций, обозначенные на кнопках калькулятора. Если такого «квадратика» нет, зажимаем кнопку Shift или «↑». На рисунке слева нужные нам параметры подчеркнуты красной линией.
Щелкаем кнопку с надписью tg или tan (тангенс) и далее « = ». Калькулятор вычисляет значение функции обратной тангенсу — арктангенс. Это значение и будет искомым углом.

Вместо Win-калькулятора можно использовать, например, онлайн-калькуляторы тригонометрических функций. Найти такие сервисы в интернете достаточно легко, задав поиск в браузере.

Важно помнить!

Измерения на местности проводим как можно точнее и рейку устанавливаем точно по уровню. Имейте в виду, что если длина рейки пусть даже полтора-два метра, а длина отрезка АВ метров 15-20, то даже незначительное отклонение уровня от горизонтали дает существенную погрешность. Тем не менее это разумный способ.  Он позволяет, пусть и не совсем точно, определить угол наклона рельефа местности.
Используя подобие треугольников АВС и СDЕ можно вычислить также перепад высот: h=АВ*DE/ DС.

| Permalink

Как измерять угол склона методом маятника

25.01.2016

4 минуты на чтение

Анна Ханкевич

VK

TG

Фрирайдер Анна Ханкевич пошагово рассказывает, как определить угол склона и потенциальную лавиноопасность с помощью простых лыжных палок.

Фрирайдер Анна Ханкевич пошагово объясняет, как определить угол склона и потенциальную лавиноопасность с помощью простых лыжных палок.

Хочу рассказать про то, как измерять угол склона. У меня есть волшебный бипер PIEPS DSP Prо, у которого есть функция измерения наклона. Она включается нажатием кнопки Scan (сканирование) и работает в режиме передачи. Но он есть не у всех. Поэтому я хочу рассказать о методе маятника (который к своему стыду, узнала совсем недавно из методички Сергея Веденина). Многим известно, что приблизительно можно прикинуть угол склона по расстоянию от вытянутой руки стоящего человека до склона. если расстояние примерно равно палке — угол около 30 если расстояние примерно равно ледорубу — угол около 45 если касаешься пальцами склона — угол около 60

Но этот способ подходит только для грубой оценки. Однако зачастую нам надо узнать угол более точно. Диапазон от 25 до 40 является самым лавиноопасным, и умение анализировать наклон важно.

Также для скитура умение на взгляд точно определить угол склона крайне важно, ведь при углах выше 20-25 градусов мы начинаем проскальзывать при движении прямо вверх и нужно перейти к траверсам. Однако, нам надо определять угол со стороны, заранее. Поэтому рекомендую постоянно тренироваться, прикидывая угол на взгляд и потом проверяя свою оценку с помощью метода маятника. Также для передачи информации необходимо точно знать численные значения. (И скептически улыбаться, когда твой приятель уверяет, что катал по 55-градусному склону).

Метод маятника позволяет определить угол склона с точностью до нескольких градусов и не требует никаких специальных приспособлений, кроме обычных палок, которые у лыжника всегда с собой=) Только палки должны быть одной длины. Шаг первый Находясь на склоне, положите палку вниз по линии падения воды ручкой вниз. Можно провести засечку на снегу у конца ручки.

Шаг второй Теперь поднимайте эту палку вверх, оставляя острие палки на снегу. Подставьте вторую палку, соединив их рукоятками, при этом вторая палка должна прийти в вертикальное положение (можно представить вторую палку как отвес).

Засеките расстояние от засечки на снегу до острия второй палки. Если расстояние равно нулю, то есть если острие вертикальной палки воткнулось точно в отметку — угол склона равен 30 градусам. Если острие выше по склону, чем засечка — то угол меньше 30 градусов. Если острие ниже по склону, чем засечка — то угол больше 30 градусов. Но я обещала точное количественное значение градусов. Для этого прикиньте расстояние между острием и засечкой в сантиметрах, каждые 10 см — это разница в три градуса.  То есть если палка-отвес воткнулась ниже засечки на 20 см, то угол склона 36 градусов, если выше по склону на 10 см — то угол склона 27 градусов. Ну и хочу напомнить, что уклон в градусах и процентах — не одно и то же-)

Безопасного и интересного катания!

• Как выбрать…
  18.07.2023

  Палки для трейлраннинга: виды и критерии выбора

  Сенькина Дарья

• Советы и инструкции
  17.07.2023

  Участие в спасработах

  Чикин Артём

• Как выбрать…
  10.07.2023

  Как правильно выбрать и использовать солнцезащитные средства

• Советы и инструкции
  05.07.2023

  Метеорология: погода в горах

  Уголькова Мария

Угол наклона и наклон линии

Пусть прямая l пересекает ось x в точке A. Угол между положительной осью x и линией l, измеренный против часовой стрелки, называется углом наклона прямой l.

На приведенном выше рисунке, если θ – это угол прямой линии l, то мы имеем следующие важные моменты.

(i) 0° ≤ θ ≤ 180°

(ii)  Для горизонтальных линий θ = 0° или 180° и для вертикальных линий θ = 90°

(iii)  Если прямая линия первоначально лежит вдоль оси х и начинает вращаться вокруг неподвижной точки А на оси х против часовой стрелки и, наконец, совпадает с осью х, то угол наклона прямой линии в начальном положении равен 0°, а угол наклона прямой – в конечном положении – 0°.

(iv)  Линии, перпендикулярные оси x, называются вертикальными линиями.

(v)  Линии, перпендикулярные оси Y, называются горизонтальными линиями.

(vi)  Другие линии, которые не перпендикулярны ни оси x, ни оси y, называются наклонными линиями.

Угол наклона и наклон линии – приложение

Основное применение угла наклона прямой линии – определение уклона.

Если θ – угол наклона прямой линии l, то tanθ называется наклоном градиента линии и обозначается буквой «m».

Следовательно, наклон прямой равен

м  = tan θ 

для 0° ≤ θ ≤ 180°

Найдем наклон прямой по приведенной выше формуле

(i)  Для горизонтальных линий угол наклона равен 0° или 180°.

То есть

θ = 0° или 180°

Следовательно, наклон прямой линии равен

м = tan0° или tan 180°  = 0

клинация 90°.

То есть

θ = 90°

Следовательно, наклон прямой равен

м  =  tan90°  =  Не определено

(iii) Для наклонных линий, если θ имеет острую форму, наклон положительный. Если же θ тупой, то наклон отрицательный.

Наклон линии — положительный или отрицательный, нулевой или неопределенный

Когда мы смотрим на прямую линию визуально, мы можем легко узнать знак наклона.

Чтобы узнать знак наклона прямой, всегда нужно смотреть на прямую слева направо.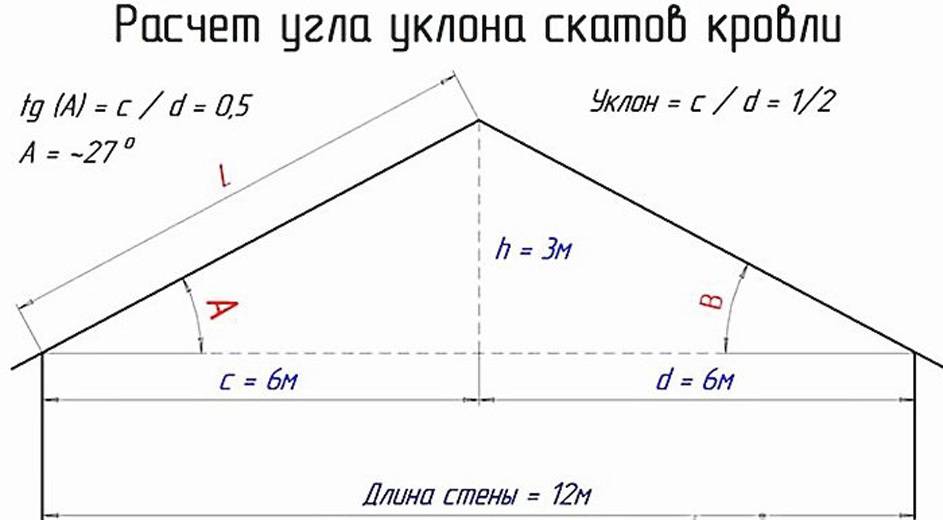

Это иллюстрируют приведенные ниже рисунки.

Решенные задачи

Задача 1 :

Найдите угол наклона прямой, наклон которой равен 1/√3.

Решение :

Пусть θ — угол наклона линии.

Тогда уклон линии равен

м  =  tanθ

Дано : Уклон = 1/√3

Тогда,  

1/√3  =  tanθ

θ =  30°

Итак, угол наклона равен 30°.

Задача 2 :

Если угол наклона прямой равен 45°, найдите ее наклон.

Решение :

Пусть θ — угол наклона линии.

Тогда, наклон линии,

м  =  tanθ

Дано: θ  =  45°

Тогда,

м  =  tan 45°

м =  1

Итак, наклон равен 1. 

Задача 3 :

Если угол наклона прямой равен 30°, найдите ее наклон.

Решение :

Пусть θ — угол наклона линии.

Затем, наклон линии,

м = tanθ

Дано: θ = 30°

Тогда

м = tan30°

м = 1/√3

900 02 Итак, наклон равен 1/√3.

Задача 4 :

Найдите угол наклона прямой, наклон которой равен √3.

Решение :

Пусть θ — угол наклона линии.

Затем, наклон линии,  

м  = tanθ

Дано: Уклон  =  √3

Тогда, 

√3  =  tanθ  

θ  = 60°

Итак, угол наклона равен 60°.

Задача 5 :

Найдите угол наклона прямой, уравнение которой y = x + 32.

Решение :

Пусть θ — угол наклона линии.

Данное уравнение находится в форме пересечения наклона.

То есть,

y = mx + b

Сравнивая

y = x + 32

и

y = mx + b,

получаем наклон m = 1, 

Мы знаем, что наклон линии равен

м  =  tanθ

Тогда

1  =  tanθ

θ  = 45°

Итак, угол наклона равен 4 5°.

Пожалуйста, отправьте свой отзыв на [email protected]

Мы всегда ценим ваши отзывы.

©Все права защищены. onlinemath5all.com

4.3 Наклон линии | Аналитическая геометрия

4.

3 Наклон линии (EMBGD)

На диаграмме показано, что прямая образует угол \(\theta\) с положительной осью \(x\). Это называется
угол наклона прямой.

Мы замечаем, что если градиент изменяется, то значение \(\theta\) также изменяется, поэтому угол
наклон линии связан с ее градиентом. Мы знаем, что градиент – это отношение изменения
\(y\)-направление на изменение \(x\)-направления:

\[m=\frac{\Delta y}{\Delta x}\]

Из тригонометрии мы знаем, что функция тангенса определяется как отношение:

\[\tan \theta = \frac{\text{противоположная сторона}}{\text{прилегающая сторона}}\]

А из схемы мы видим, что

\начать{выровнять*}
\tan \theta &= \dfrac{\Delta y}{\Delta x} \\
\поэтому m &= \tan \theta \qquad \text{ for } \text{0}\text{°} \leq \theta < \текст{180}\текст{°} \конец{выравнивание*}

Следовательно, градиент прямой линии равен тангенсу угла, образованного между прямой и
положительное направление оси \(x\).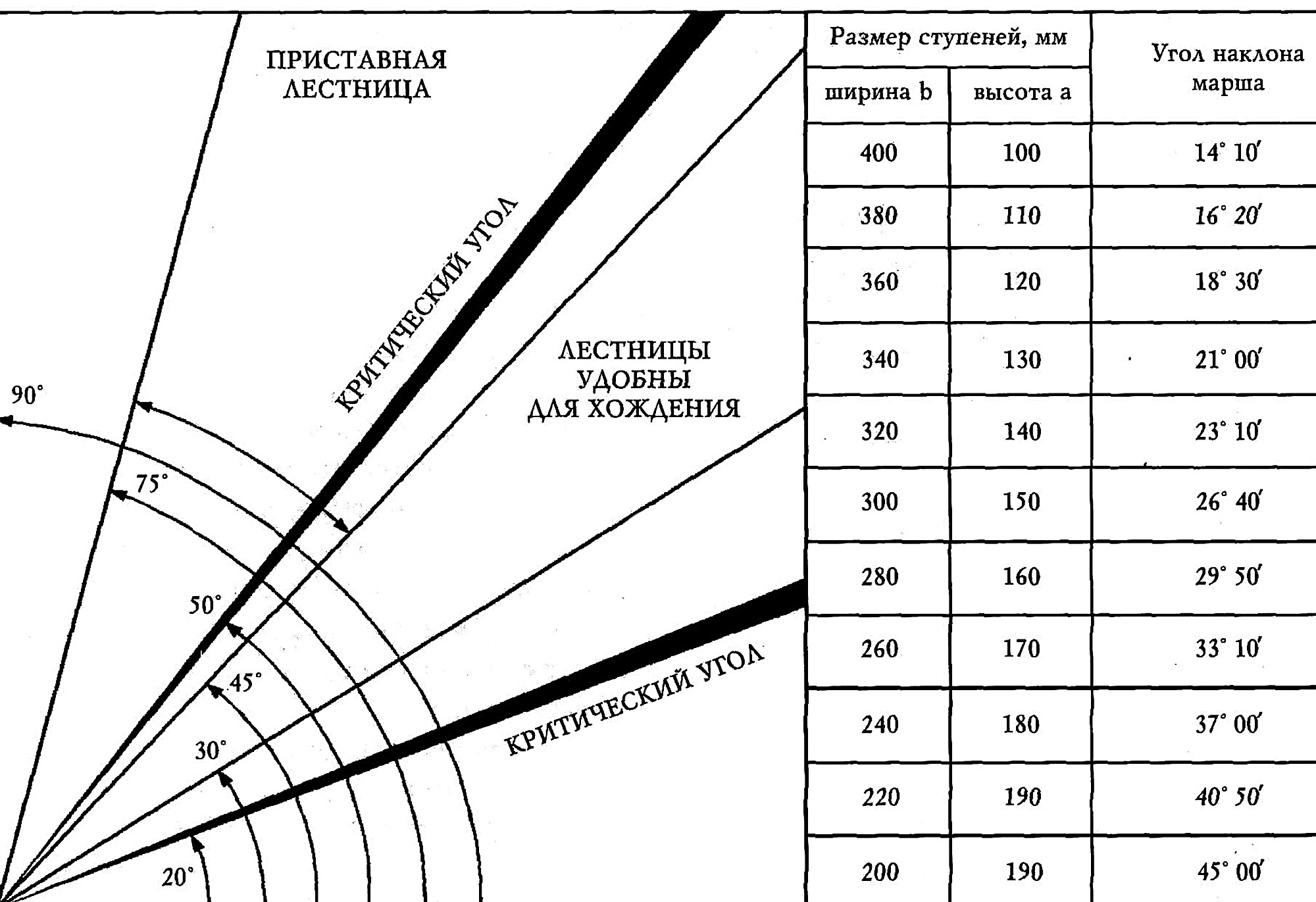

Вертикальные линии

• \(\тета = \текст{90}\текст{°}\)
• Градиент не определен, так как значения \(x\) не изменились (\(\Delta x = 0\)).
• Следовательно, \(\tan \theta\) также не определено (график \(\tan \theta\) имеет асимптоту в \(\theta =
  \text{90}\text{°}\)).

Горизонтальные линии

• \(\тета = \текст{0}\текст{°}\)
• Градиент равен \(\text{0}\), поскольку значения \(y\) не изменяются (\(\Delta y = 0\)).
• Следовательно, \(\tan \theta\) также равно \(\text{0}\) (график \(\tan \theta\) проходит через
  происхождение \((\text{0}\text{°};0))\).

Линии с отрицательным уклоном

Если прямая имеет отрицательный наклон (\(m < 0\), \(\tan \theta < 0\)), то угол, образованный между прямой и положительным направлением оси \(х\) тупая.

Из диаграммы CAST в тригонометрии мы знаем, что функция тангенса отрицательна во втором и четвертом
квадрант. Если мы вычисляем угол наклона для линии с отрицательным градиентом, мы должны добавить
\(\text{180}\text{°}\), чтобы изменить отрицательный угол в четвертом квадранте на тупой угол в
второй квадрант:

Если нам дана прямая с градиентом \(m = -\text{0,7}\), то мы можем определить угол
наклон с помощью калькулятора: 9{-1}(-\текст{0,7}) \\
&= -\текст{35,0}\текст{°}
\конец{выравнивание*}

Этот отрицательный угол лежит в четвертом квадранте. Мы должны добавить \(\text{180}\)\(\text{°}\) чтобы получить тупой
угол во втором квадранте:

\начать{выровнять*}
\тета &= -\текст{35,0}\текст{°} + \текст{180}\текст{°} \\
&= \текст{145}\текст{°}
\конец{выравнивание*}

И мы всегда можем использовать наш калькулятор, чтобы проверить, что тупой угол \(\theta = \text{145}\text{°}\)
дает градиент \(m = -\text{0,7}\).

Угол наклона

Учебник Упражнение 4.5

\(\text{60}\text{°}\)

\begin{align*}
м &= \загар \тета\\
&= \tan \text{60}\text{°} \\
\поэтому m &= \text{1,7}
\end{align*}

\(\text{135}\text{°}\)

\begin{align*}
м &= \загар \тета\\
&= \tan \text{135}\text{°} \\
\поэтому m &= -\text{1}
\end{выравнивание*}

\(\text{0}\text{°}\)

\begin{align*}
м &= \загар \тета\\
&= \tan \text{0}\text{°} \\
\поэтому m &= \text{0}
\end{align*}

\(\text{54}\text{°}\)

\begin{align*}
м &= \загар \тета\\
&= \загар \текст{54}\текст{°} \\
\поэтому m &= \text{1,4}
\end{выравнивание*}

\(\text{90}\text{°}\)

\begin{align*}
м &= \загар \тета\\
&= \загар \текст{90}\текст{°} \\
\поэтому m & \text{ не определено}
\end{align*}

\(\text{45}\text{°}\)

\begin{align*}
м &= \загар \тета\\
&= \tan \text{45}\text{°} \\
\поэтому m &= \text{1}
\end{выравнивание*}

\(\text{140}\text{°}\)

\begin{align*}
м &= \загар \тета\\
&= \tan \text{140}\text{°} \\
\поэтому m &= -\text{0,8}
\end{align*}

\(\text{180}\text{°}\)

\begin{align*}
м &= \загар \тета\\
&= \tan \text{180}\text{°} \\
\поэтому m &= \text{0}
\end{выравнивание*} 9{-1} \влево( \text{0,75} \вправо) \\
\поэтому \тета &= \text{36,8}\text{°}
\end{align*}

\(2y — x = 6\)

\begin{align*}
2у — х&=6\
2у &= х + 6 \\
y &= \frac{1}{2}x + 3 \\
\загар \тета &= м \\
&= \фракция{1}{2} \\
\theta &= \tan^{-1} \left( \text{0,5} \right) \\
\поэтому \тета &= \текст{26,6}\текст{°}
\end{выравнивание*} 9{-1} \влево( \текст{1} \вправо) \\
\поэтому \тета &= \text{45}\text{°}
\end{align*}

\(y=4\)

Горизонтальная линия

\(x = 3y + \frac{1}{2}\)

\begin{align*}
х &= 3y + \frac{1}{2} \\
x — \frac{1}{2} &= 3y \\
\frac{1}{3}x — \frac{1}{6} &= y \\
\поэтому m &= \frac{1}{3} \\
\theta &= \tan^{-1} \left( \frac{1}{3} \right) \\
\поэтому \тета &= \text{18,4}\text{°}
\end{выравнивание*} 9{-1} \влево( \text{0,577} \вправо) \\
\поэтому \тета &= \текст{30}\текст{°}
\конец{выравнивание*}

Рабочий пример 8: Наклон прямой линии

Определить угол наклона (с точностью до \(\text{1}\) десятичного знака) прямой линии
проходящей через точки \((2;1)\) и \((-3;-9)\). {-1}2\\
&= \текст{63,4}\текст{°}
\end{выравнивание*}

Важно: убедитесь, что ваш калькулятор находится в режиме DEG (градусы).

Напишите окончательный ответ

Угол наклона прямой равен \(\text{63,4}\)\(\text{°}\).

temp text

Рабочий пример 9: Наклон прямой линии

Определите уравнение прямой, проходящей через точку \((3;1)\) и с углом
наклон \(\text{135}\text{°}\).

Используйте угол наклона для определения градиента линии

\begin{align*}
м &= \загар \тета\\
&= \tan \text{135}\text{°} \\
\поэтому m &= -1
\конец{выравнивание*}

Запишите градиентно-точечную форму уравнения прямой линии

\[y — y_1 = m(x — x_1)\]

Подставьте \(m = -1\)

\[y — y_1 = -(x — x_1)\]

Подставьте заданную точку \ ((3;1)\)

\begin{выравнивание*}
у — 1 & = -(х — 3) \\
у&=-х+3+1\
&= -х + 4
\конец{выравнивание*}

Напишите окончательный ответ

Уравнение прямой линии \(y = -x + 4\).

temp text

Рабочий пример 10: Наклон прямой линии

Определить острый угол (с точностью до \(\text{1}\) десятичного знака) между прямой, проходящей через
точки \(M(-1;1\frac{3}{4})\) и \(N(4;3)\) и прямая \(y = — \frac{3}{2}x + 4\).

Начертить эскиз

Начертить линию через точки \(M(-1;1\frac{3}{4})\) и \(N(4;3)\) и линию \(y = — \frac{3}{2}x
+ 4\) в подходящей системе координат. Обозначьте \(\alpha\) и \(\beta\) углы наклона
две строки. Обозначьте \(\theta\) острый угол между двумя прямыми.

Обратите внимание, что \(\alpha\) и \(\theta\) — острые углы, а \(\beta\) — тупой угол.

\[\begin{массив}{rll}
\hat{B}_1 &= \text{180}\text{°} — \beta & (\angle \text{на строке}) \\
\text{and} \theta &= \alpha + \hat{B}_1 \quad & (\text{ext.} \angle \text{ of } \triangle =
\text{ сумма внутр. опп}) \\
\поэтому \тета &= \альфа + (\текст{180}\текст{°} — \бета) \\
&= \text{180}\text{°} + \alpha — \beta
\конец{массив}\]
9{-1} \left(-\frac{3}{2}\right) &= -\text{56,3}\text{°}
\конец{выравнивание*}

Этот отрицательный угол лежит в четвертом квадранте. Мы знаем, что угол наклона \(\beta\) равен
тупой угол, лежащий во второй четверти, поэтому

\начать{выравнивать*}
\beta &= -\text{56,3}\text{°} + \text{180}\text{°}\\
&= \текст{123,7}\текст{°}
\конец{выравнивание*}

Определить градиент и угол наклона линии через \(M\) и \(N\)

Определение градиента
\начать{выравнивать*}
m & = \frac{y_2 — y_1}{x_2 — x_1} \\
& = \dfrac{3 — \frac{7}{4}}{4-(-1)} \\
& = \dfrac{\frac{5}{4}}{5} \\
&= \фракция{1}{4}
\end{align*}

Определить угол наклона
\начать{выравнивать*}
\загар \альфа & = м\\
& = \фракция{1}{4} \\
\поэтому \alpha & = \tan^{-1} \left( \frac{1}{4} \right) \\
&= \текст{14,0}\текст{°}
\end{выравнивание*}

Напишите окончательный ответ

\begin{align*}
\тета & = \текст{180}\текст{°} + \альфа — \бета\\
& = \text{180}\text{°} + \text{14,0}\text{°} — \text{123,7}\text{°} \\
& = \текст{70,3}\текст{°}
\end{align*}

Острый угол между двумя прямыми равен \(\text{70,3}\)\(\text{°}\).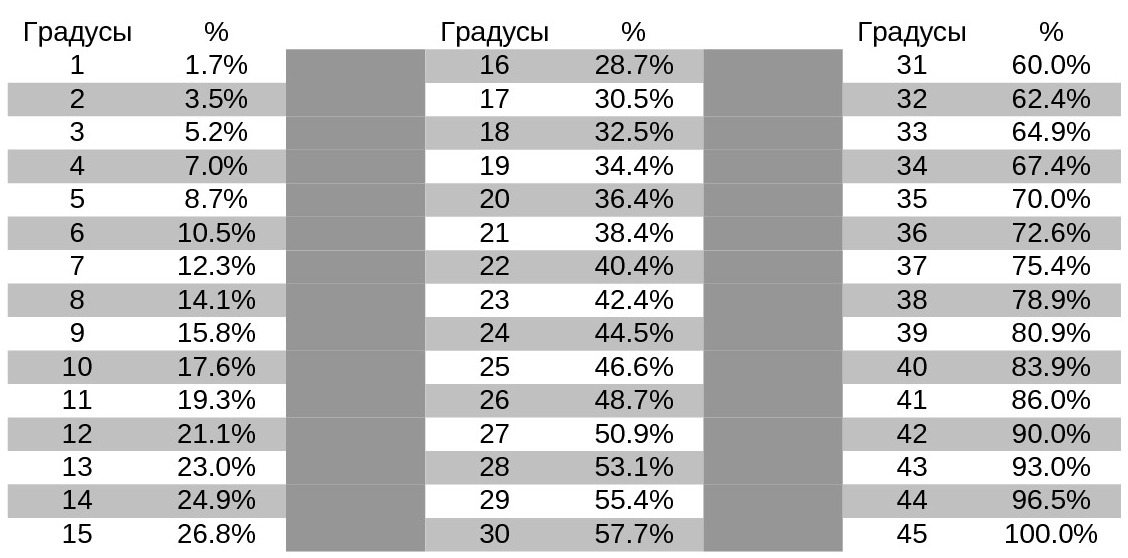 {-1} \left( -\text{2} \right) \\
&= -\текст{63,4}\текст{°} \\
\поэтому \theta &= \text{180}\text{°} — \text{63,4}\text{°} \\
\поэтому \тета &= \text{80}\text{°}
\end{выравнивание*} 9{-1} \влево(-\frac{9}{2} \вправо) \\
&= -\текст{77,5}\текст{°} \\
\поэтому \тета &= \text{180}\text{°} — \text{77,5}\text{°} \\
\поэтому \тета &= \текст{102,5}\текст{°}
\end{align*}

линия, проходящая через \((-1;-6)\) и \((-\frac{1}{2};-\frac{11}{2})\)

\begin{align*}
m &= \frac{y_2 -y_1}{x_2 — x_1} \\
&= \frac{-\frac{11}{2}+ 6}{-\frac{1}{2}+1} \\
&= \ гидроразрыва {\ гидроразрыва {1} {2}} {\ гидроразрыва {1} {2}} \\
\поэтому m &= 1 \\
\theta &= \tan^{-1} \left( 1 \right) \\
\поэтому \тета &= \text{45}\text{°}
\end{выравнивание*} 9{-1} \влево(-\frac{1}{3} \вправо) \\
\поэтому \тета &= -\текст{18,4}\текст{°} \\
\поэтому \тета &= \text{180}\text{°} — \text{18,4}\text{°} \\
\поэтому \тета &= \текст{161,6}\текст{°}
\end{align*}

Градиент undefined

Определить острый угол между линией, проходящей через точки \(A(-2;\frac{1}{5})\)
и \(B(0;1)\) и прямой, проходящей через точки \(C(1;0)\) и \(D(-2;6)\). {-1} \left(-2 \right) \\
\поэтому \alpha &= -\text{63,4}\text{°} \\
\поэтому \alpha &= \text{180}\text{°} — \text{63,4}\text{°} \\
\поэтому \alpha &= \text{116,6}\text{°} \\
\text{And } \theta &= \beta + (\text{180}\text{°} — \alpha) \quad (\text{ext. } \angle
\треугольник)\\
\поэтому \theta &= \text{21,8}\text{°} + (\text{180}\text{°} —
\text{116,6}\text{°} ) \\
&= \текст{85,2}\текст{°}
\конец{выравнивание*}

Определить угол между прямой \(y + x = 3\) и прямой \(x = y + \frac{1}{2}\).

Пусть угол наклона линии \(y + x = 3\) равен \(\alpha\), а угол наклона
наклон линии \(x = y + \frac{1}{2}\) равен \(\beta\). Пусть угол между двумя
строки будут \(\тета\):

\начать{выравнивать*}
у &= — х + 3 \\
\поэтому m &= — 1 \\
\alpha &= \tan^{-1} \left(-1\right) \\
\поэтому \alpha &= -\text{45}\text{°} \\
\поэтому \alpha &= \text{180}\text{°} — \text{45}\text{°} \\
\поэтому \alpha &= \text{135}\text{°} \\
х &= у + \ гидроразрыва {1} {2} \\
х — \фракция{1}{2} &= у \\
\поэтому m &= 1 \\
\beta &= \tan^{-1} \left(1 \right) \\
\поэтому \бета &= \text{45}\text{°} \\
\text{And } \theta &= \beta + (\text{180}\text{°} — \alpha) \quad (\text{ext.