Как проверить прямой угол: простая технология
Чтобы проверить прямой угол, поможет очень старая и простая столярная хитрость. По сути, эта базовая хитрость и не хитрость вовсе. Она основана на теореме Пифагора, которая гласит «Сумма квадратов катетов прямоугольного треугольника равна квадрату гипотенузы». Звучит сложно? Вовсе нет! Давайте разбираться.
Что вы узнаете
Как проверить прямой угол
Если вы хотите проверить, является ли ваше изделие или какая-то его часть строго прямоугольными, используя математику, сделайте следующее. Выберите один угол и с помощью комбинированного угольника предварительно проверьте, действительно ли он является прямым. Затем с помощью рулетки измерьте длину одной из сторон, составляющей прямой угол, и на калькуляторе умножьте полученное число на само себя (или, иными словами, возведите его в квадрат). Запишите это число или сохраните в памяти калькулятора.
Затем измерьте длину второй стороны, которая составляет прямой угол. Проделайте ту же операцию – умножьте это число на само себя. Затем сложите полученное число с тем, которые вы записали до этого. Одна часть уравнения готова!
Проделайте ту же операцию – умножьте это число на само себя. Затем сложите полученное число с тем, которые вы записали до этого. Одна часть уравнения готова!
Чтобы получить третью величину, измерьте расстояние от свободного конца одной стороны до свободного конца другой стороны. Это будет гипотенузой. Умножьте длину гипотенузы на саму себя. Если полученное число совпадает с суммой, которую вы получили до этого (когда складывали квадраты двух сторон), то угол действительно прямой.
Как проверить прямоугольник?
В столярном деле часто используют так называемое «правило 3-4-5». Вы всегда можете использовать его, чтобы определить прямой угол по любой шкале при разметке.
Однако есть более точный (и гораздо более быстрый) способ определить, является ли ваше изделие прямоугольным. Просто измерьте диагонали предполагаемого прямоугольника. Если диагональ, проведённая из левого нижнего в правый верхний угол в точности совпадает по длине с диагональю, проведённой из правого нижнего в левый верхний угол, то элементы действительно составляют прямоугольник.
А что же делать, если их длины не совпали? Скорректируйте изделие. Выберите ту диагональ, которая получилась длиннее, и слегка подтолкните один из её углов внутрь. После этого повторите измерения. Продолжайте корректировать положение до тех пор, пока длины диагоналей не буду совпадать.
Просто? Конечно! Теперь и вы можете использовать этот способ в своей работе.
Автор статьи: Александра
Изучаю инженерное проектирование, механику, архитектуру и дизайн. Люблю создавать вещи своими руками
Как проверить прямой угол в помещении с помощью рулетки — подсказка Древних Египтян🗿 | Дизайнерский ремонт👷
Расскажу, как я за 9 секунд проверяю прямые углы в ходе замеров новостройки, пользуясь лишь рулеткой.
В каждой квартире есть углы, которые необходимо вывести под 90 град. Это углы, в которых будет устанавливаться корпусная мебель: кухонный гарнитур, встроенные шкафы.
Есть также маленькие помещения, такие как гардеробная, ванная и санузел, где все углы будут заставлены сантехприборами, шкафчиками и стеллажами.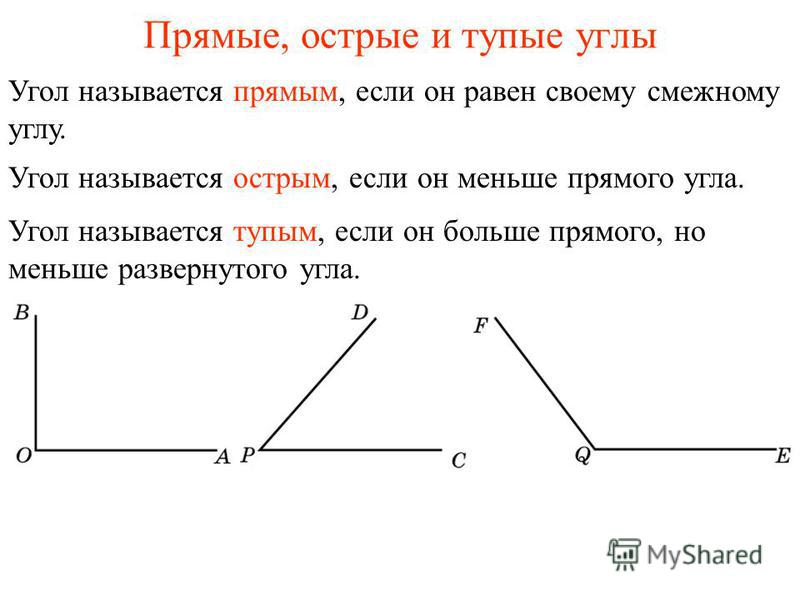 Здесь все углы должны быть прямыми.
Здесь все углы должны быть прямыми.
Есть 2 причины, чтобы проверить эти углы до начала ремонта.
Прорабу и новоселу
Чтобы правильно рассчитать ремонтный бюджет (смету), нужно учитывать каждый угол, который придется приводить к 90 град. Эта работа долгая и поэтому требует отдельной оплаты.
Дизайнеру и новоселу
При разработке планировки необходимо учитывать реальные чистовые размеры помещений.
В маленьком санузле важен каждый сантиметр. Если дизайнер расставит сантехприборы и мебель, не проверив прямые углы, это может привести к ошибке.
В процессе ремонта для получения прямых углов стены отштукатурят и все размеры «съедут». В результате, проходы станут узкими и неудобными и планировку придется переделывать.
Как проверить все нужные углы, если у вас собой только рулетка?
Очень просто. В основу положен принцип «египетского треугольника»
Известно, что еще в Древнем Египте этот принцип использовался при строительстве пирамид с прямоугольным основанием.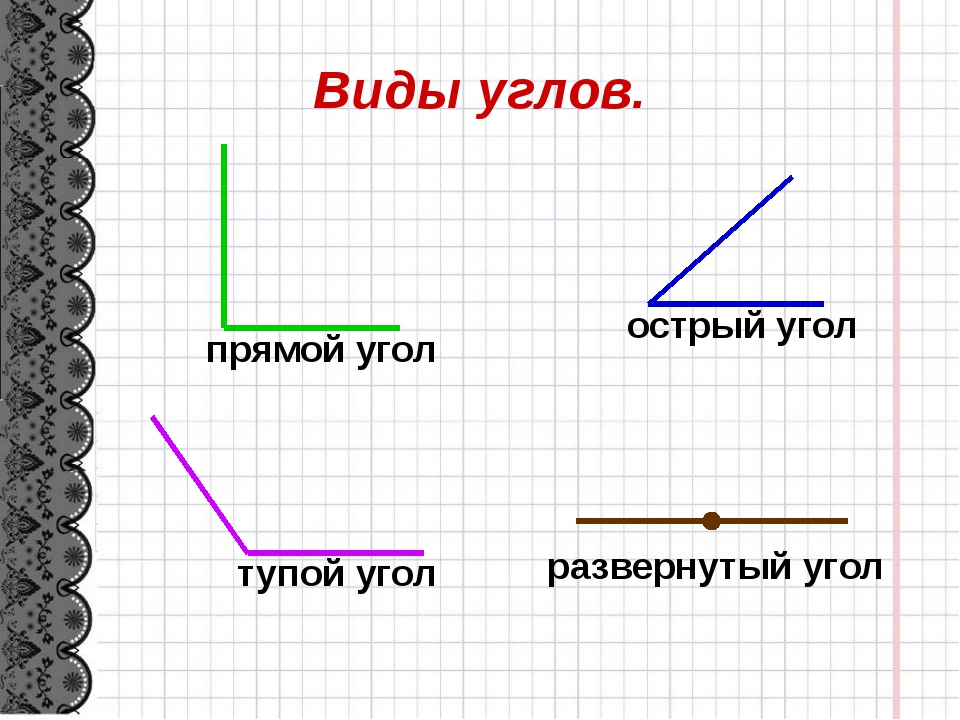
При строительстве таких громадных сооружений угольником не обойдешься)))
Фото Карты Google
Фото Карты Google
Египетским треугольником называется треугольник со сторонами длиной 3, 4, 5 единиц
Он имеет прямой угол там, где сходятся стороны, длиной 3 и 4.
Чтобы проверить в помещении прямой угол или нет, достаточно отложить от угла в разные стороны отрезки, кратные 3 и 4.
Например, отложите от угла в одну сторону 30 см и сделайте отметку, на другой стене отметьте 40 см от того же угла.
Теперь осталось только измерить расстояние между отметками. Если оно равно 50 см — угол прямой, если меньше — угол острый, больше — угол тупой.
Как проверить внешний угол — прямой он или нет, — читайте в комментариях. И добавляйте свои идеи!
Ставьте палец вверх и подписывайтесь на канал https://zen.yandex.ru/remont_school , чтобы видеть больше интересных статей про интерьер и ремонт.
Самые популярные публикации канала:
Как я ищу честных строителей для ремонта квартиры
К а к у з н а т ь ч т о с к р ы в а е т ч е л о в е к , з а д а в 1 в о п р о с
Лучший плинтус для натяжного потолка
Д е н ь г и и з в о з д у х а в х о д е р е м о н т а д о м а и ш т у к а т у р к и с т е н
Не выносите вид грязной мыльницы? Есть современная стильная альтернатива
Почему потеют пластиковые окна изнутри дома
К а к у ю п л и т к у в ы б р а т ь д л я в а н н о й и н а п о л , ч т о б ы н е п р и ш л о с ь е е в ы к и д ы в а т ь — Р е к о м е н д а ц и и д и з а й н е р а
Обидная ошибка с гипсокартоном большинства мастеров
Проверяем прямой угол с помощью лазерного уровня
Сегодня вы научитесь с помощью лазерного уровня проверять соответствие угла 90°. Для этого вам всего лишь нужно следовать пошаговой инструкции, подготовленной специалистом нашей компании.
Для этого вам всего лишь нужно следовать пошаговой инструкции, подготовленной специалистом нашей компании.
Пошаговая инструкция:
Шаг первый. Выставьте лазерный нивелир вдоль первой стены, для этого:
1. От одного края проверяемой стены отмерьте 10 см с помощью рулетки. Поставьте карандашом на полу или стене отметку. Если отделка чистовая, используйте малярный скотч как поверхность для отметки (наклейте его на пол или на стену и разметьте по нему).
2. С помощью рулетки отложите от другого края проверяемой стены 10 см. Поставьте отметку карандашом на полу или на стене.
3. Поставьте лазерный нивелир в углу примыкания двух проверяемых стен, на расстоянии 30-35 см от второй проверяемой стены.
4. Включите отображение вертикальных плоскостей.
5. Нацельте вертикальную плоскость на ближайшую отметку.
6. Путем передвижения построителя плоскостей к или от первой проверяемой стены, выставьте лазерный уровень так, чтобы его вертикальная плоскость проходила через обе поставленные отметки.
Шаг второй. На лазерном уровне включите отображение перпендикулярной вертикальной плоскости.
Шаг третий. Вдоль поверхности проверяемой стены с помощью рулетки замерьте расстояние от первой проверяемой стены до первой построенной плоскости.
Шаг четвертый. Теперь сверьте это расстояние с изначальным (10 см). Если расстояние больше 10 см, значит на этом месте яма. Если расстояние меньше 10 см, значит на этом месте бугор.
Шаг пятый. Затем с помощью рулетки замерьте расстояние от первой проверяемой стены до первой построенной плоскости по высоте первой проверяемой стены
Шаг шестой. И сверьте это расстояние с изначальным (10 см). Если расстояние больше 10 см, значит проверяемая стена завалена от вас. Если расстояние меньше 10 см, значит проверяемая стена завалена на вас.
Шаг седьмой. Повторяем пункты 3,4,5,6 этой инструкции в отношении второй проверяемой стены.
Запомните: Если расстояния между краями первой и краями второй стен попарно одинаково расположены от заданных плоскостей, то угол между этими двумя примыкающими стенами соответствует 90 градусов.
Если хоть одна из стен дальним краем направлена от вас, угол тупой.
Если хоть одна из стен дальним краем направлена к вам, угол между стенами острый.
Посмотрите наше портфолио и убедитесь в этом лично
Также вы можете посмотреть, как проверить прямой угол с помощью лазерного уровня в формате видео. Это займет у вас чуть больше 1 минуты. Не забудьте поставить лайк, если ролик окажется для вас полезным.
Виды углов: острый, прямой, тупой, развёрнутый, выпуклый и полный
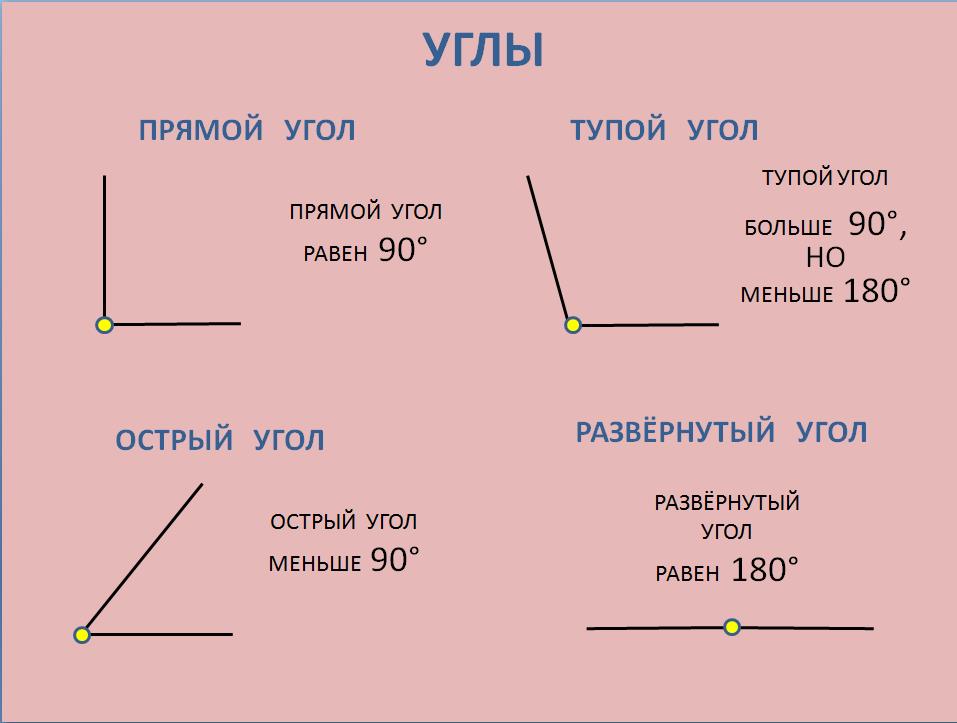
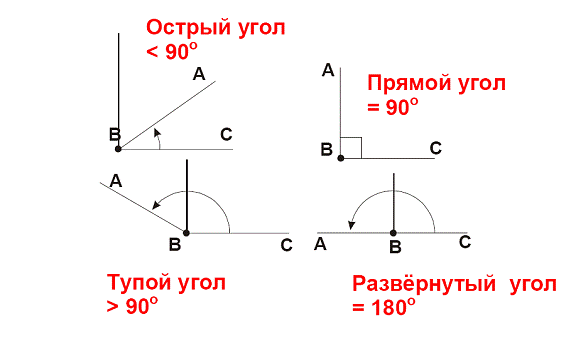
Каждый угол, в зависимости от его величины, имеет своё название:
- Острый угол — это угол, который меньше прямого угла (<90°).
- Прямой угол — это угол, стороны которого перпендикулярны друг другу.
 Прямой угол обозначается буквой d и равен 90°.
Прямой угол обозначается буквой d и равен 90°.Если два смежных угла равны между собой, то каждый из них называется прямым углом. Прямой угол обычно обозначается не дугой, а уголком:
∠AOC и ∠COB — прямые углы. Общая сторона прямых углов OC называется перпендикуляром к прямой AB, а точка O — основанием перпендикуляра.Сумма двух прямых углов равна развёрнутому углу, значит, прямой угол равен половине развёрнутого угла.
- Тупой угол — это угол, который больше прямого угла, но меньше развёрнутого:
90° < тупой угол < 180°.
- Развёрнутый угол — это угол, образованный двумя дополнительными лучами.
Развёрнутый угол равен сумме двух прямых углов или, короче, двум прямым углам. Следовательно, развёрнутый угол равен 180° или 2d.
Все развёрнутые углы равны между собой.
- Выпуклый угол — это угол, который больше развёрнутого угла, но меньше полного:
180° < выпуклый угол < 360°.

- Полный угол — это угол, обе стороны которого совпадают с одним лучом.
Полный угол равен сумме четырёх прямых углов, то есть 4d (360°).
Прилежащие углы
Прилежащие углы — это пара углов, имеющих общую вершину и общую сторону, другие стороны которых лежат по разные стороны от общей стороны.
∠AOB и ∠BOC — прилежащие углы, O — общая вершина, OB — общая сторона.
Если из вершины любого угла провести луч, разделяющий угол на два угла, то образованные углы будут прилежащими.
Угол, разделённый лучом, будет называться суммой полученных углов, например угол AOB является суммой углов AOC и COB:
∠AOB = ∠AOC + ∠COB.
Каждый из прилежащих углов, ∠AOC и ∠COB, называется разностью углов AOB и другого прилежащего, то есть:
∠AOC = ∠AOB — ∠COB,
∠COB = ∠AOB — ∠AOC.
Полезная геометрия | Наука и жизнь
В школе мы несколько лет подряд прилежно изучаем геометрию. Но не зря ли мы тратим время? Чем может помочь геометрия в жизни? Измерить расстояние от точки до точки, вычислить площадь или объём предмета и только? Нет, конечно. Законы геометрии применимы буквально на каждом шагу. Просто нужно знать, как ими воспользоваться.
Вешаем зеркало
Вы решили повесить в прихожей зеркало. Тут же возникает вопрос: какой минимальной высоты должно быть зеркало, чтобы человек среднего роста мог видеть себя в нём целиком? И ещё: имеет ли при этом значение размер помещения, где будет висеть зеркало? Решение. Предмет и его отражение симметричны относительно плоскости зеркала. Построим в нём изображение человека (рис. 1): АВ — человек, А1В1 — его изображение, точка С — глаз, DE — зеркало. Из рисунка видно, что минимальная высота зеркала приблизительно равна половине роста человека, считая от уровня глаз. При этом высота Е нижнего края зеркала от пола должна быть вдвое меньше расстояния от пола до глаз. Легко понять, что, на каком бы расстоянии от такого зеркала ни находился человек, он сможет увидеть себя в нём с головы до ног, значит, размер помещения значения не имеет.
При этом высота Е нижнего края зеркала от пола должна быть вдвое меньше расстояния от пола до глаз. Легко понять, что, на каком бы расстоянии от такого зеркала ни находился человек, он сможет увидеть себя в нём с головы до ног, значит, размер помещения значения не имеет.
Завариваем чай
Перед вами стеклянные чайники четырёх моделей одинаковой вместимости (рис. 2). В каком чайнике заваренный чай останется тёплым дольше? Решение. Из курса физики известно, что время охлаждения пропорционально площади поверхности тела. Значит, чем меньше поверхность чайника, тем дольше остывает чай. Самая маленькая площадь поверхности у четвёртого чайника, так как его форма близка к сфере (S = d2).
Выдерживаем прямые углы
Если вы решили склеить коробку, сделать шкатулку или выложить плитку, важно, чтобы все детали были точными прямоугольниками или квадратами. В противном случае всё пойдёт наперекосяк. Как проверить, имеет ли деталь нужную «геометрию»? Решение. Чтобы проверить, у всех ли деталей, с которыми вы работаете, прямые углы и одинаковые линейные размеры, можно использовать строи-тельный угольник (рис. 3), а можно применить знания по геометрии. Убедитесь в том, что противоположные стороны четырёхугольника равны и при этом диагонали тоже имеют одинаковую длину. Как вы и сами знаете, сделать это можно с помощью линейки. Но вот вопрос: обязательно ли проверять и стороны и диагонали? Геометрия утверждает, что да! Например, на рис. 4 диагонали в четырёхугольнике слева равны, но очевидно, что его углы совсем не прямые. А в четырёхугольнике справа противоположные стороны равны, но это тоже не прямоугольник. Для проверки прямоугольности геометрия ещё советует убедиться в равенстве всех четырёх отрезков, на которые разбиваются диагонали в точке их пересечения.
Чтобы проверить, у всех ли деталей, с которыми вы работаете, прямые углы и одинаковые линейные размеры, можно использовать строи-тельный угольник (рис. 3), а можно применить знания по геометрии. Убедитесь в том, что противоположные стороны четырёхугольника равны и при этом диагонали тоже имеют одинаковую длину. Как вы и сами знаете, сделать это можно с помощью линейки. Но вот вопрос: обязательно ли проверять и стороны и диагонали? Геометрия утверждает, что да! Например, на рис. 4 диагонали в четырёхугольнике слева равны, но очевидно, что его углы совсем не прямые. А в четырёхугольнике справа противоположные стороны равны, но это тоже не прямоугольник. Для проверки прямоугольности геометрия ещё советует убедиться в равенстве всех четырёх отрезков, на которые разбиваются диагонали в точке их пересечения.
Строим прямой угол на земле
Известен старинный способ постро-ения прямого угла на поверхности земли. Его использовали ещё древние египтяне. Они строили прямой угол с помощью обычной верёвки, на которой через равные расстояния завязаны тринадцать узелков. Чтобы отрезки на верёвке были одинаковые, узелки завязывали вокруг колышков, вбитых в землю на равном расстоянии друг от друга. В чём состоит этот «верёвочный» способ? Решение. В древности при закладке храма такую верёвку с узелками использовали для определения направлений его стен. Концы верёвки на месте крайних узелков связывали, а затем натягивали её на три колышка так, как показано на рис. 5. Стороны при этом имели соотношение 3:4:5. В таком треугольнике один из углов получается прямым. Впоследствии этот факт был доказан в теореме Пифагора. Поэтому первых геометров называли ещё «натягивателями верёвок». Нужно отметить, что таким способом построения прямого угла на местности пользуются и сегодня, например при закладке фундамента небольшого строения.
Чтобы отрезки на верёвке были одинаковые, узелки завязывали вокруг колышков, вбитых в землю на равном расстоянии друг от друга. В чём состоит этот «верёвочный» способ? Решение. В древности при закладке храма такую верёвку с узелками использовали для определения направлений его стен. Концы верёвки на месте крайних узелков связывали, а затем натягивали её на три колышка так, как показано на рис. 5. Стороны при этом имели соотношение 3:4:5. В таком треугольнике один из углов получается прямым. Впоследствии этот факт был доказан в теореме Пифагора. Поэтому первых геометров называли ещё «натягивателями верёвок». Нужно отметить, что таким способом построения прямого угла на местности пользуются и сегодня, например при закладке фундамента небольшого строения.
Проверяем перпендикулярность стен
Как проверить, перпендикулярны ли друг другу соседние стены в комнате, воспользовавшись верёвкой с узелками из предыдущей задачи? Решение. Если предположить, что стены в комнате вертикальны, а пол горизонтален, то проверку проводят так. От точки на полу в углу между стенами откладывают отрезки длиной 3 и 4 единицы (рис. 6). Если стены перпендикулярны, то расстояние между концами отрезков будет равно 5 единицам, так как построенный тре-угольник со сторонами 3, 4, 5 — прямоугольный.
От точки на полу в углу между стенами откладывают отрезки длиной 3 и 4 единицы (рис. 6). Если стены перпендикулярны, то расстояние между концами отрезков будет равно 5 единицам, так как построенный тре-угольник со сторонами 3, 4, 5 — прямоугольный.
Отмеряем нужный объём
Часто в рецептуре того или иного блюда требуется взять четверть (или половину) стакана жидкости, муки либо какого-либо другого продукта. Как отмерить такой объём с наибольшей точностью, не прибегая к дополнительным измерительным средствам? Решение. Воспользуемся стаканом цилиндрической формы — это важно для точности измерений. Чтобы отмерить четверть стакана жидкости, надо из наполненного стакана вылить столько, чтобы оставшаяся в нём жидкость закрыла половину дна (рис. 7). Она займёт примерно четверть объёма стакана-цилиндра. Аналогично поступаем, если надо отмерить половину стакана. Наклоняем стакан так, чтобы оставшаяся в нём жидкость закрыла всё дно (рис. 8). А можно ли геометрическим способом узнать объём бутылки? Конечно! Для этого надо заполнить бутылку водой чуть меньше чем наполовину (рис. 9, слева) и измерить объём воды, умножив площадь дна бутылки на высоту налитой в неё воды (напомним, что объём цилиндра вычисляется как произведение площади основания на высоту). Затем нужно перевернуть бутылку горлышком вниз так, чтобы вода не вытекла, и измерить объём верхней цилиндрической части бутылки, оставшейся пустой (рис. 9, справа). Полный объём бутылки равен сумме найденных объёмов. Для точности можно учесть толщину стенок бутылки.
9, слева) и измерить объём воды, умножив площадь дна бутылки на высоту налитой в неё воды (напомним, что объём цилиндра вычисляется как произведение площади основания на высоту). Затем нужно перевернуть бутылку горлышком вниз так, чтобы вода не вытекла, и измерить объём верхней цилиндрической части бутылки, оставшейся пустой (рис. 9, справа). Полный объём бутылки равен сумме найденных объёмов. Для точности можно учесть толщину стенок бутылки.
Укрепляем калитку
Прямоугольная калитка (рис. 10, слева) со временем расшатывается и становится похожей на параллело-грамм. Этого можно избежать, прибив к ней ещё одну планку. Только надо знать, как это сделать. Решение. Выбор такого положения планки, как показано на рис. 10, справа, основан на свойстве жёсткости треугольника. Оно гласит: существует единственный треугольник с заданными длинами сторон. Планка и есть гипотенуза такого треугольника.
Выбираем табурет
Если вы решили предыдущую задачу, то без труда определите, на какой табурет (рис. 11) можно сесть без риска оказаться на полу. Решение. Безопасный табурет изображён на правой картинке, так как его сиденье и ножки образуют треугольник.
11) можно сесть без риска оказаться на полу. Решение. Безопасный табурет изображён на правой картинке, так как его сиденье и ножки образуют треугольник.
Исправляем ошибку кроя
Предположим, вам нужно вырезать для аппликации два разносторонних треугольника из цветной бумаги — «левый» и «правый». Вы случайно вырезали их одинаковыми — оба «левые». Можно ли, не используя новый кусок бумаги, исправить ошибку? Решение. Для исправления ошибки вы можете разрезать один из треугольников, например так, как показано на рис. 12, а затем сложить из него нужный треугольник.
Находим середину
Как без всяких измерений найти середину негнущегося прута, доски или металлического стержня? Решение. Можно отмерить размеры стержня на шнуре, затем сложить его пополам и отложить полученную длину. А можно воспользоваться геометрическим построением середины отрезка с помощью циркуля и линейки, если, конечно, размеры позволяют это сделать. Ещё более рациональное решение даёт физика. Середину однородного стержня легко найти, используя понятие центра тяжести (рис. 13).
Середину однородного стержня легко найти, используя понятие центра тяжести (рис. 13).
Наука и жизнь // Иллюстрации
Наука и жизнь // Иллюстрации
Наука и жизнь // Иллюстрации
Наука и жизнь // Иллюстрации
Наука и жизнь // Иллюстрации
Наука и жизнь // Иллюстрации
Наука и жизнь // Иллюстрации
Наука и жизнь // Иллюстрации
Наука и жизнь // Иллюстрации
Наука и жизнь // Иллюстрации
Наука и жизнь // Иллюстрации
Наука и жизнь // Иллюстрации
‹
›
Как сделать прямой угол для фундамента. Общие правила для любого фундамента
Как сделать прямой угол для фундамента. Общие правила для любого фундамента
Выбираем точку отсчета. Первую сторону нашего фундамента нужно привязать к какому-нибудь объекту нашего участка.
Пример. Сделаем так, чтобы наш фундамент (дом) был параллелен одной из сторон забора. Следовательно, первую бечевку натягиваем равноудалено от этой стороны забора на нужное нам расстояние.
Следовательно, первую бечевку натягиваем равноудалено от этой стороны забора на нужное нам расстояние.
Построение прямого угла (90⁰). В качестве примера будем рассматривать прямоугольный фундамент, в котором все углы максимально близки к 90⁰.
Существует несколько способов как это сделать. Мы рассмотрим 2 основных. © www.gvozdem.ru
Способ 1. Правило золотого треугольника
Для построения прямого угла будем применять теорему Пифагора.
Формула
Чтобы не углубляться в геометрию попробуем описать проще. Чтобы между двумя отрезками a и b сделать угол в 90⁰ нужно сложить длины этих отрезков и вывести корень из этой суммы. Получившиеся число будет являться длинной нашей диагонали соединяющей наши отрезки. Очень просто расчет сделать с помощью калькулятора.
Обычно при разметке фундамента берут размеры сторон, чтобы при выведении из корня получалось целое число. Пример: 3х4х5; 6х8х10.
Если у вас есть рулетка, то в целом проблем не возникнет, если вы будете брать отрезки отличные от общеиспользуемых. Например: 3х3х4,24; 2х2х2,83; 4х6х7,21
Например: 3х3х4,24; 2х2х2,83; 4х6х7,21
Если измерения мы производили в метрах, то значения получаются очень даже понятными: 4м24см; 2м83см; 7м21см.
Калькулятор
Также стоит отметить, что измерения можно производить в любых системах измерения длины главное использовать известное нам соотношение сторон: 3х4х5 метра, 3х4х5 сантиметра и т.п. То есть, если даже у вас нет инструмента для измерения длины, то можно взять, например, рейку (длина рейки не имеет значения) и померить ей (3 рейки х 4 рейки х 5 реек).
Теперь давайте посмотрим как это применить на практике.
Как найти прямой угол на земле. Как пользоваться правилом 3-4-5
1
Поймите, в чем суть правила 3-4-5. Если у треугольника есть три стороны со значениями 3, 4 и 5 см (или кратное им значение), это прямоугольный треугольник, угол между сторонами с меньшими значениями составляет 90 градусов. Если у вас получилось построить треугольник, исходя из значений угла, то можно точно сказать, что угол прямоугольный. Это правило основано на теореме Пифагора :A2+ B2= C2(в прямоугольном треугольнике). Где С – самая длинная сторона (гипотенуза), А и В –остальные стороны (катеты).
Это правило основано на теореме Пифагора :A2+ B2= C2(в прямоугольном треугольнике). Где С – самая длинная сторона (гипотенуза), А и В –остальные стороны (катеты).
- Правило 3-4-5 очень удобно проверить благодаря целым числам. Итак, опираясь на математические расчеты:32+ 42= 9 + 16 = 25 =52.
2
Отмерьте от угла 3 см (или 3 м) на одной стороне. Можно взять любую меру длины. Пометьте отмеренный участок точкой.
- Можно умножить каждое число на одно и то же число – и это правило все равно сработает. Например, это правило будет работать для треугольника со сторонами 30-40-50 сантиметров или метров. Если у вас большая комната, можно использовать следующие числа: 9-12-15, 6-8-10 метров.
3
Отмерьте четыре метра (или длину со значением, которое кратно четырем) на другой стороне. То же самое, если у вас получится сделать треугольник, то угол между этими двумя сторонами будет равен 90 градусам. Снова пометьте отмеренный участок точкой.
Снова пометьте отмеренный участок точкой.
4
Теперь измерьте расстояние между этими двумя метками. Если расстояние кратно пяти, то можно точно сказать, что угол составляет 90 градусов.
- Если расстояние меньше, чем 5 единиц (метров), значит, угол острый (меньше 90 градусов). Если есть такая возможность, нужно немного раздвинуть стороны, образующие этот угол.
- Если расстояние между метками составляет больше 5 единиц (метров), значит, угол тупой (то есть больше 90 градусов). Если есть такая возможность, нужно свести стороны, образующие угол, поближе друг к другу, чтобы угол получился прямым. Строя прямой угол, можно использовать прямой угол рамки.
- Получив прямой угол в 90 градусов, можно проверить остальные углы комнаты, чтобы убедиться в том, что они прямые.
Как ровно разметить фундамент. Подготовка к разметке фундамента
Перед тем как разметить фундамент своими руками составляется проект будущего здания . При этом определяется площадь объекта, внешний вид строения и планировка отдельных помещений. Проект привязывается к участку, где будет проводиться строительство. Сначала проводятся работы по исследованию грунта, а затем осуществляется разметка основания.
Проект привязывается к участку, где будет проводиться строительство. Сначала проводятся работы по исследованию грунта, а затем осуществляется разметка основания.
Для проведения разметки потребуются следующие инструменты:
- Колышки из металла или дерева.
- Строительные уровни.
- Рулетка и отвес.
- Нивелир и лазерный дальномер.
- Шнур.
- Доски и обрезки арматуры.
Перед тем как сделать разметку под фундамент, необходимо произвести подготовительные работы:
- Демонтируются старые строения , убирается мусор и лишние насаждения на участке.
- Площадка выравнивается в горизонтальной плоскости , устраняются все углубления и холмы.
- Подготавливается проезд для транспортных средств, которые будут подвозить строительные материалы и вывозить ненужный мусор. После очищения дороги, ее рекомендуется присыпать гравием для удобного проезда во время дождя.
- Отдельно подготавливается место для складирования разнообразных материалов.

- Перед строительными работами стоит возвести забор, чтобы защитить строительные материалы.
- Продумайте подведение электричества , воды, монтаж санузла, а также временное жилье.
После этого проводится разметка фундамента под дом. Технология монтажа предполагает наличие прямоугольных форм. Общие правила и нормы для разметки подходят для всех разновидностей оснований, на них не влияет материал изготовления или наличие подвального помещения.
Разметка начинается с любой стороны строения . Это может быть фасад или боковая часть постройки. При использовании рулетки стоит отдать предпочтение изделиям из металла, которые имеют длину более 10 м. Модели из ткани не гарантируют точность измерений и провисают при замерах.
Для осуществления обноски рекомендуется использовать бруски (не менее 10 штук), колья (примерно 19 штук), а также шнуры, доски и веревки. Иногда применяются куски арматуры, которые вбиваются в грунт. Они должны быть п-образной формы.
Участок выбирается с учетом следующих факторов:
- Перспектива проведения всех коммуникаций.

- Состояние дорог.
- Географическая привязка к сторонам света .
Важнейшим предназначением разметки является осуществление правильной ориентации будущего строения, относительно местности. Это позволит возвести строение с учетом стандартных технологических правил.
Видео как отмерить прямой угол в помещении или на местности без угольника
Разметка фундамента: углы и диагонали
Разметка фундамента: углы и диагонали. Разметка фундамента – это процесс перенесения размеров будущей конструкции с плана на участок. Разметку фундамента следует проводить грамотно и точно, так как от качественного выполнения данной работы зависит ровность будущего фундамента и соответственно сооружения возводимого на нём. Так же изначальная точная и ровная разметка поможет избежать ошибок в последующих строительных работах.
Для разметки фундамента используют колья, шпагат и рулетку.
При проведении работ по разметки фундамента следует соблюдать определённые правила:
- Установку первого колышка угла фундамента следует проводить, согласно плану застройки, учитывая СНиП. От первого колышка откладывается расстояние равное расстоянию стен фундамента в одну сторону и в другую, желательно с небольшим запасом.
- Две выставленные стороны должны образовать прямой угол. Чтобы проверить ровность угла следует применить правило «египетского» треугольника. «Египетский» треугольник, согласно теореме Пифагора, имеет катеты длинной 3 и 4, и гипотенузу равную 5. Выбор единицы меры не имеет значения. От образованного двумя сторонами угла, в одну сторону откладываем 3 м, а в другую 4 м и фиксируем отмеренное расстояние с помощью либо прищепки, либо узелка из шпагата. Меряем расстояние от одного узелка до другого, должно получиться 5 м. Значит угол прямой. По такому же принципу выставляем две оставшиеся стороны.
- Когда все углы выровнены, начинаем проверять диагонали фундамента.
 Для начала, их следует высчитать математическим способом по уравнению корень квадратный из а2 + в2. Например, если стороны фундамента 8 и 10, диагональ будет равна 64 (8х8) + 100 (10х10) =»164, вычисляем корень из 164, получаем 12,8. Наша диагональ равна 12,8. У прямоугольников и квадратов диагонали равны.
Для начала, их следует высчитать математическим способом по уравнению корень квадратный из а2 + в2. Например, если стороны фундамента 8 и 10, диагональ будет равна 64 (8х8) + 100 (10х10) =»164, вычисляем корень из 164, получаем 12,8. Наша диагональ равна 12,8. У прямоугольников и квадратов диагонали равны. - При выставлении опалубки все углы и диагонали ещё раз внимательно перепроверяются.
- Часто встречаются фундаменты не правильной формы, с различными выступами и нишами. В этом случае, для грамотной разметки фундамента, необходимо разделить его на прямоугольники или квадраты. Если стены образуют не прямой угол, то обозначают контур, а затем вычитаем или прибавляем прямоугольный треугольник.
Информацию о строительстве фундамента можно узнать по телефону +7 (812) 918-82-93 или отправить нам заявку на расчет
Предлагаем услуги по строительству монолитных фундаментов для загородного дома в Санкт-Петербурге и Ленинградской области с высоким качеством проводимых работ и по разумным ценам.
Нахождение угла в прямоугольном треугольнике
Угол с любых двух сторон
Мы можем найти неизвестный угол в прямоугольном треугольнике, если нам известны длины двух его сторон .
Пример
Лестница прислонена к стене, как показано.
Что такое угол между лестницей и стеной?
Ответ — использовать синус, косинус или тангенс!
Но какой использовать? У нас есть специальная фраза «SOHCAHTOA», чтобы помочь нам, и мы используем ее так:
Шаг 1 : найдите имен двух известных нам сторон
- Соседний примыкает к углу,
- Напротив , напротив угла
- , а самая длинная сторона — Гипотенуза .
Пример: в нашем примере лестницы нам известна длина:
- сторона Напротив угол «х», который равен 2,5
- самая длинная сторона, называемая Гипотенуза , что составляет 5
Шаг 2 : теперь используйте первые буквы этих двух сторон ( O pposite и H ypotenuse) и фразу «SOHCAHTOA», чтобы найти, какой из синуса, косинуса или тангенса использовать:
SOH. | S ine: sin (θ) = O pposite / H ypotenuse |
… CAH … | C осин: cos (θ) = A djacent / H ypotenuse |
… TOA | T Угол: tan (θ) = O pposite / A djacent |
В нашем примере это O pposite и H ypotenuse, и это дает нам « SOH cahtoa», что говорит нам, что нам нужно использовать Sine .
Шаг 3 : Поместите наши значения в уравнение синуса:
S дюйм (x) = O pposite / H ypotenuse = 2,5 / 5 = 0,5
Шаг 4 : Теперь решите это уравнение!
грех (х) = 0,5
Далее (поверьте мне на данный момент) мы можем преобразовать это в это:
х = грех -1 (0,5)
Затем возьмите наш калькулятор, введите 0,5 и используйте кнопку sin -1 , чтобы получить ответ:
х = 30 °
И у нас есть ответ!
Но что означает
sin -1 …?
Итак, функция синуса «sin» принимает угол и дает нам соотношение «противоположность / гипотенуза»,
Но sin -1 (так называемый «обратный синус») идет другим путем. ..
..
… это
принимает соотношение «противоположная сторона / гипотенуза» и дает нам угол.
Пример:
- Синус Функция: sin ( 30 ° ) = 0,5
- Функция обратной синусоиды: sin -1 ( 0,5 ) = 30 °
| На калькуляторе нажмите одну из следующих кнопок (в зависимости от от вашей марки калькулятора): либо «2ndF sin», либо «shift sin». |
На своем калькуляторе попробуйте использовать sin и sin -1 , чтобы увидеть, какие результаты вы получите!
Также попробуйте cos и cos -1 . И tan и tan -1 .
Давай, попробуй.
Шаг за шагом
Вот четыре шага, которые нам нужно выполнить:
- Шаг 1 Найдите две известные нам стороны — противоположную, смежную и гипотенузу.

- Шаг 2 Используйте SOHCAHTOA, чтобы решить, какой из Sine, Cosine или Tangent использовать в этом вопросе.
- Шаг 3 Для синуса вычислить противоположное / гипотенузу, для косинуса вычислить смежное / гипотенузу или для касательного вычислить противоположное / смежное.
- Шаг 4 Найдите угол с помощью калькулятора, используя один из следующих значений: sin -1 , cos -1 или tan -1
Примеры
Давайте посмотрим на еще пару примеров:
Пример
Найдите угол подъема
плоскости из точки А на земле.
- Шаг 1 Две известные нам стороны — это O pposite (300) и A djacent (400).
- Шаг 2 SOHCAH TOA сообщает нам, что мы должны использовать T angent.
- Шаг 3 Вычислить напротив / рядом = 300/400 = 0,75
- Шаг 4 Найдите угол с помощью калькулятора, используя tan -1
Tan x ° = напротив / рядом = 300/400 = 0. 75
75
tan -1 из 0,75 = 36,9 ° (с точностью до 1 знака после запятой)
Если не указано иное, углы обычно округляются до одного десятичного знака.
Пример
Найдите величину угла a °
- Step 1 Две известные нам стороны: A djacent (6750) и H ypotenuse (8100).
- Step 2 SOH CAH TOA сообщает нам, что мы должны использовать осин C .
- Шаг 3 Вычислить смежный / гипотенузу = 6,750 / 8,100 = 0,8333
- Шаг 4 Найдите угол с помощью калькулятора, используя cos -1 из 0,8333:
cos a ° = 6,750 / 8,100 = 0,8333
cos -1 из 0,8333 = 33,6 ° (с точностью до 1 знака после запятой)
Калькулятор прямоугольного треугольника | Найдите a, b, c и угол
Найти недостающую сторону или угол проще простого, чем с помощью нашего замечательного инструмента — стороны прямоугольного треугольника и калькулятора углов. Выберите два заданных значения, введите их в калькулятор, и оставшиеся неизвестные будут определены в мгновение ока! Если вам интересно, как найти недостающую сторону прямоугольного треугольника, продолжайте прокручивать, и вы найдете формулы, лежащие в основе нашего калькулятора.
Выберите два заданных значения, введите их в калькулятор, и оставшиеся неизвестные будут определены в мгновение ока! Если вам интересно, как найти недостающую сторону прямоугольного треугольника, продолжайте прокручивать, и вы найдете формулы, лежащие в основе нашего калькулятора.
Как найти стороны прямоугольного треугольника
Есть несколько методов получения длин сторон прямоугольного треугольника. В зависимости от того, что дано, вы можете использовать разные отношения или законы, чтобы найти недостающую сторону:
- С учетом двух сторон
Если вы знаете две другие стороны прямоугольного треугольника, это самый простой вариант; все, что вам нужно сделать, это применить теорему Пифагора:
a² + b² = c²
, если отрезок
aявляется недостающей стороной, преобразовать уравнение к форме, когда a находится на одной стороне, и извлечь квадратный корень:a = √ (c² - b²), если участок
bнеизвестен, тоb = √ (c² - a²)для гипотенузы c отсутствует, формула
c = √ (a² + b²)
- Заданный угол и гипотенуза
Примените закон синусов или тригонометрии, чтобы найти длины сторон прямоугольного треугольника:
- Заданный угол и одна ножка
Найдите недостающую ногу с помощью тригонометрических функций:
a = b * tan (α)b = a * tan (β)
- Заданная площадь и одна нога
Как мы помним из основной формулы площади треугольника, мы можем вычислить площадь, умножив высоту и основание треугольника и разделив результат на два. Прямоугольный треугольник — это частный случай разностороннего треугольника, в котором одна ножка является высотой, а вторая ножка является основанием, поэтому уравнение упрощается до:
Прямоугольный треугольник — это частный случай разностороннего треугольника, в котором одна ножка является высотой, а вторая ножка является основанием, поэтому уравнение упрощается до:
площадь = a * b / 2
Например, если мы знаем только площадь прямоугольного треугольника и длину участка a , мы можем вывести уравнение для других сторон:
-
b = 2 * площадь / а -
c = √ (a² + (2 * площадь / a) ²)
Как найти угол прямоугольного треугольника
Если вы знаете, что один угол отличается от прямого, вычисление третьего угла несложно:
Дано β : α = 90 - β
Дано α : β = 90 - α
Однако, если заданы только две стороны треугольника, определение углов прямоугольного треугольника требует применения некоторых основных тригонометрических функций:
для α
-
sin (α) = a / c, поэтомуα = arcsin (a / c)(обратный синус) -
cos (α) = b / c, поэтомуα = arccos (b / c)(обратный косинус) -
tan (α) = a / b, поэтомуα = arctan (a / b)(арктангенс) -
cot (α) = b / asoα = arccot (b / a)(обратный котангенс)
и для β
-
sin (β) = b / c, поэтомуβ = arcsin (b / c)(обратный синус) -
cos (β) = a / c, поэтомуβ = arccos (a / c)(обратный косинус) -
tan (β) = b / a, поэтомуβ = arctan (b / a)(арктангенс) -
cot (β) = a / bsoβ = arccot (a / b)(обратный котангенс)
Как решить прямоугольный треугольник с одной стороной?
Чтобы собрать треугольник с одной стороной, вам также понадобится , один из непрямых углов . В противном случае это невозможно:
В противном случае это невозможно:
- Если у вас есть гипотенуза , умножьте ее на sin (θ) , чтобы получить длину стороны , противоположной углу.
- Либо умножьте гипотенузу на cos (θ), чтобы получить сторону, примыкающую к углу.
- Если у вас есть сторона без гипотенузы, смежная с углом , разделите ее на cos (θ) , чтобы получить длину гипотенузы .
- Либо умножьте эту длину на tan (θ), чтобы получить длину стороны, противоположной углу.
- Если у вас есть угол и сторона , противоположная , вы можете разделить длину стороны на sin (θ) , чтобы получить гипотенузу .
- Или разделите длину на tan (θ), чтобы получить длину стороны, примыкающей к углу.
Как найти недостающую сторону прямоугольного треугольника? Как найти угол? Пример
Давайте покажем, как найти стороны прямоугольного треугольника с помощью этого инструмента:
- Предположим, мы хотим найти недостающую сторону, заданную площадь и одну сторону.
 Выберите нужный вариант из раскрывающегося списка . Это третий.
Выберите нужный вариант из раскрывающегося списка . Это третий. - Введите указанные значения . Например, площадь прямоугольного треугольника равна 28 кв. Дюйм, а b = 9 дюймов.
- Наш калькулятор сторон и углов прямоугольного треугольника отображает недостающие стороны и углы! Теперь мы знаем, что:
- a = 6,222 дюйма
- c = 10,941 дюйм
- α = 34,66 °
- β = 55,34 °
Теперь давайте проверим, как работает поиск углов прямоугольного треугольника:
- Обновите калькулятор. Выберите нужный вариант . Предположим, что у нас есть две стороны, и мы хотим найти все углы. Вариант по умолчанию — правильный.
- Введите длину стороны . В нашем прямоугольном треугольнике гипотенуза равна 13 дюймов, а катет a = 5 дюймов.
- Отсутствует сторона и углы . В нашем примере b = 12 дюймов, α = 67,38 ° и β = 22,62 °.

Сколько линий симметрии у прямоугольного треугольника?
Если прямоугольный треугольник равнобедренный (т.е., его две негипотенузные стороны имеют одинаковую длину) он имеет одну линию симметрии . В противном случае треугольник будет иметь без линий симметрии .
Может ли прямоугольный треугольник иметь равные стороны?
Нет, у прямоугольного треугольника все 3 стороны не могут быть равны , так как все три угла также не могут быть равны, , поскольку один должен быть 90 ° по определению. Однако у прямоугольного треугольника две стороны, не являющиеся гипотенузой, могут быть равны по длине. Это также будет означать, что два других угла равны 45 °.
Все ли прямоугольные треугольники похожи?
Не все прямоугольные треугольники похожи на , хотя некоторые могут быть такими же. Они похожи, если все их углы имеют одинаковую длину или если соотношение двух сторон одинаково.
Калькулятор прямоугольного треугольника
Укажите 2 значения ниже, чтобы рассчитать другие значения прямоугольного треугольника. Если в качестве единицы измерения угла выбраны радианы, он может принимать такие значения, как пи / 3, пи / 4 и т. Д.
Калькулятор связанных треугольников | Калькулятор по теореме Пифагора
Прямой треугольник
Прямоугольный треугольник — это тип треугольника, угол которого составляет 90 °.Правые треугольники и отношения между их сторонами и углами являются основой тригонометрии.
В прямоугольном треугольнике сторона, противоположная углу 90 °, является самой длинной стороной треугольника и называется гипотенузой. Стороны прямоугольного треугольника обычно называют переменными a, b и c, где c — гипотенуза, а a и b — длины более коротких сторон. Их углы также обычно обозначаются с использованием заглавной буквы, соответствующей длине стороны: угол A для стороны a, угол B для стороны b и угол C (для прямоугольного треугольника это будет 90 °) для стороны c, как показано ниже.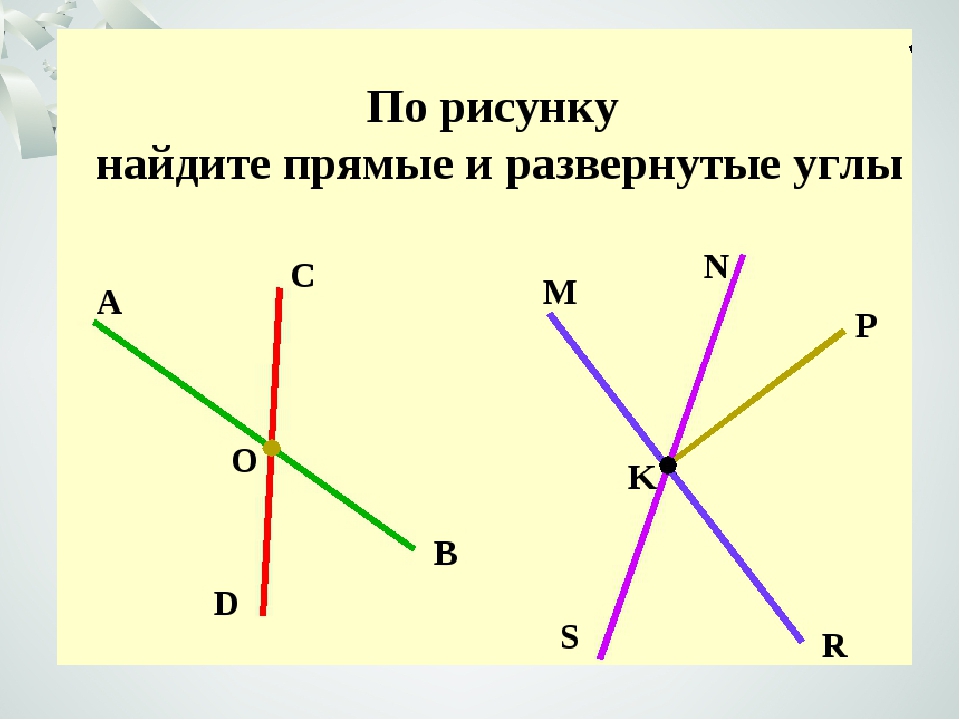 .В этом калькуляторе для обозначения неизвестных угловых величин используются греческие символы α (альфа) и β (бета). h относится к высоте треугольника, которая представляет собой длину от вершины прямого угла треугольника до гипотенузы треугольника. Высота делит исходный треугольник на два меньших, похожих треугольника, которые также похожи на исходный треугольник.
.В этом калькуляторе для обозначения неизвестных угловых величин используются греческие символы α (альфа) и β (бета). h относится к высоте треугольника, которая представляет собой длину от вершины прямого угла треугольника до гипотенузы треугольника. Высота делит исходный треугольник на два меньших, похожих треугольника, которые также похожи на исходный треугольник.
Если все три стороны прямоугольного треугольника имеют целые числа, он известен как треугольник Пифагора.В треугольнике этого типа длины трех сторон в совокупности известны как тройка Пифагора. Примеры включают: 3, 4, 5; 5, 12, 13; 8, 15, 17 и т. Д.
Площадь и периметр прямоугольного треугольника рассчитываются так же, как и любого другого треугольника. Периметр — это сумма трех сторон треугольника, а площадь можно определить с помощью следующего уравнения:
Специальные прямоугольные треугольники
Треугольник 30 ° -60 ° -90 °:
30 ° -60 ° -90 ° относится к угловым измерениям в градусах этого типа специального прямоугольного треугольника.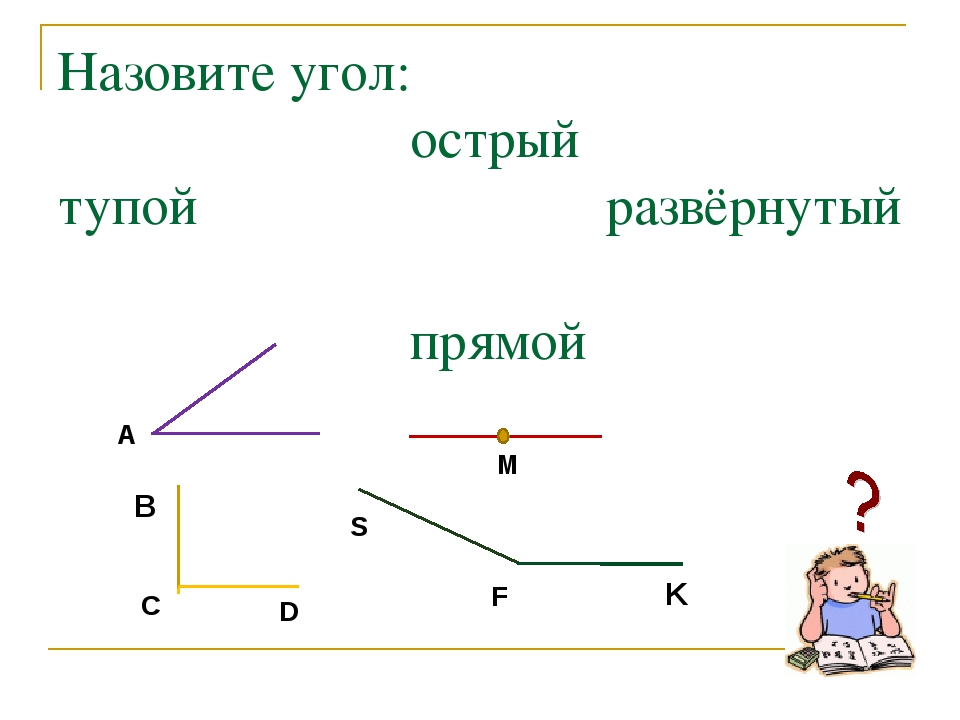 В этом типе прямоугольного треугольника стороны, соответствующие углам 30 ° -60 ° -90 °, имеют соотношение 1: √3: 2. Таким образом, в этом типе треугольника, если длина одной стороны и соответствующий угол стороны известны, длина других сторон может быть определена с использованием указанного выше соотношения. Например, учитывая, что сторона, соответствующая углу 60 °, равна 5, пусть a — длина стороны, соответствующей углу 30 °, b — длина стороны 60 °, а c — длина стороны 90 °. сторона .:
В этом типе прямоугольного треугольника стороны, соответствующие углам 30 ° -60 ° -90 °, имеют соотношение 1: √3: 2. Таким образом, в этом типе треугольника, если длина одной стороны и соответствующий угол стороны известны, длина других сторон может быть определена с использованием указанного выше соотношения. Например, учитывая, что сторона, соответствующая углу 60 °, равна 5, пусть a — длина стороны, соответствующей углу 30 °, b — длина стороны 60 °, а c — длина стороны 90 °. сторона .:
Углы: 30 °: 60 °: 90 °
Соотношение сторон: 1: √3: 2
Длина сторон: a: 5: c
Тогда, используя известные отношения сторон этого особого типа треугольника:
Как видно из вышеизложенного, знание только одной стороны треугольника 30 ° -60 ° -90 ° позволяет относительно легко определить длину любой из других сторон.Этот тип треугольника можно использовать для вычисления тригонометрических функций, кратных π / 6.
45 ° -45 ° -90 ° треугольник:
Треугольник 45 ° -45 ° -90 °, также называемый равнобедренным прямоугольным треугольником, поскольку он имеет две стороны равной длины, представляет собой прямоугольный треугольник, в котором стороны, соответствующие углам, составляют 45 ° -45 ° -90 °, соблюдайте соотношение 1: 1: √2. {2}} [/ latex].
{2}} [/ latex].
Ключевые термины
- ножки : стороны, прилегающие к прямому углу в прямоугольном треугольнике.
- прямоугольный треугольник : [латекс] 3 [/ латекс] -сторонняя форма, где один угол имеет значение [латекс] 90 [/ латекс] градусов
- гипотенуза : сторона, противоположная прямому углу треугольника, и самая длинная сторона прямоугольного треугольника.
- Теорема Пифагора : Сумма площадей двух квадратов на ножках ([латекс] a [/ латекс] и [латекс] b [/ латекс]) равна площади квадрата на гипотенузе ([ латекс] с [/ латекс]).\ circ [/ latex]). Прямоугольный треугольник — это треугольник, в котором один угол является прямым. Соотношение сторон и углов прямоугольного треугольника является основой тригонометрии.
Сторона, противоположная прямому углу, называется гипотенузой (на рисунке сторона [латекс] c [/ латекс]). Боковые стороны, прилегающие к прямому углу, называются ножками (стороны [латекс] a [/ латекс] и [латекс] b [/ латекс]).
 Сторона [латекс] a [/ латекс] может быть идентифицирована как сторона, прилегающая к углу [латекс] B [/ латекс] и противоположная (или противоположная) углу [латекс] A [/ латекс].Сторона [латекс] b [/ латекс] — это сторона, прилегающая к уголку [латекс] A [/ латекс] и противоположная уголку [латекс] B [/ латекс].
Сторона [латекс] a [/ латекс] может быть идентифицирована как сторона, прилегающая к углу [латекс] B [/ латекс] и противоположная (или противоположная) углу [латекс] A [/ латекс].Сторона [латекс] b [/ латекс] — это сторона, прилегающая к уголку [латекс] A [/ латекс] и противоположная уголку [латекс] B [/ латекс].Прямой треугольник: Теорема Пифагора может использоваться, чтобы найти значение длины недостающей стороны в прямоугольном треугольнике.
Если длины всех трех сторон прямоугольного треугольника являются целыми числами, треугольник называется треугольником Пифагора, а длины его сторон в совокупности известны как тройка Пифагора.
Теорема Пифагора
Теорема Пифагора, также известная как теорема Пифагора, является фундаментальным соотношением в евклидовой геометрии.{2}} [/ латекс]
В этом уравнении [латекс] c [/ латекс] представляет длину гипотенузы, а [латекс] a [/ латекс] и [латекс] b [/ латекс] — длины двух других сторон треугольника.

Хотя часто говорят, что знание теоремы предшествовало ему, [2] теорема названа в честь древнегреческого математика Пифагора (ок. 570 — ок. 495 до н. Э.). Ему приписывают первое записанное доказательство.
Теорема Пифагора: Сумма площадей двух квадратов на ножках ([латекс] a [/ латекс] и [латекс] b [/ латекс]) равна площади квадрата на гипотенузе ( [латекс] c [/ латекс]).2} & = \ sqrt {25} \\ c & = 5 ~ \ mathrm {cm} \ end {align}} [/ latex]
Как работают тригонометрические функции
Тригонометрические функции могут использоваться для поиска недостающих длин сторон в прямоугольных треугольниках.
Цели обучения
Узнавать, как тригонометрические функции используются для решения задач о прямоугольных треугольниках, и определять их входные и выходные данные
Основные выводы
Ключевые моменты
- Прямоугольный треугольник имеет один угол со значением 90 градусов ([latex] 90 ^ {\ circ} [/ latex]) Три тригонометрические функции, наиболее часто используемые для поиска недостающей стороны прямоугольного треугольника: [латекс ] \ Displaystyle {\ грех {т} = \ гидроразрыва {противоположный} {гипотенуза}} [/ латекс], [латекс] \ displaystyle {\ соз {т} = \ гидроразрыва {прилегающий} {гипотенуза}} [/ латекс], и [латекс] \ displaystyle {\ tan {t} = \ frac {противоположный} {смежный}} [/ latex]
Тригонометрические функции
Мы можем определить тригонометрические функции через угол [латекс] t [/ латекс] и длины сторон треугольника.
 Соседняя сторона — это сторона, ближайшая к углу. («Соседний» означает «рядом».) Противоположная сторона — это сторона, противоположная углу. Гипотенуза — это сторона треугольника, противоположная прямому углу, и она самая длинная.
Соседняя сторона — это сторона, ближайшая к углу. («Соседний» означает «рядом».) Противоположная сторона — это сторона, противоположная углу. Гипотенуза — это сторона треугольника, противоположная прямому углу, и она самая длинная.Прямой треугольник: Стороны прямоугольного треугольника по отношению к углу [латекс] t [/ латекс].
При поиске недостающей стороны прямоугольного треугольника, но единственная информация, которую вы предоставляете, — это измерение острого угла и длина стороны, используйте тригонометрические функции, перечисленные ниже:
- Синус [латекс] \ displaystyle {\ sin {t} = \ frac {напротив} {гипотенуза}} [/ латекс]
- Косинус [латекс] \ displaystyle {\ cos {t} = \ frac {соседний} {гипотенуза}} [/ латекс]
- Касательная [латекс] \ Displaystyle {\ tan {t} = \ frac {напротив} {смежный}} [/ латекс]
Тригонометрические функции равны отношениям, которые связывают определенные длины сторон прямоугольного треугольника.
 При поиске отсутствующей стороны первым делом необходимо определить, какие стороны и под каким углом даны, а затем выбрать соответствующую функцию, которая будет использоваться для решения проблемы.
При поиске отсутствующей стороны первым делом необходимо определить, какие стороны и под каким углом даны, а затем выбрать соответствующую функцию, которая будет использоваться для решения проблемы.Вычисление тригонометрической функции прямоугольного треугольника
Иногда вы знаете длину одной стороны треугольника и угол, и вам нужно найти другие измерения. Используйте одну из тригонометрических функций ([latex] \ sin {} [/ latex], [latex] \ cos {} [/ latex], [latex] \ tan {} [/ latex]), определите стороны и заданный угол , составьте уравнение и с помощью калькулятора и алгебры найдите недостающую длину стороны.{\ circ} [/ latex] и длиной гипотенузы [latex] 25 [/ latex] футов, найдите длину стороны, противоположной острому углу (округлите до ближайшей десятой):
Прямой треугольник: Дан прямоугольный треугольник с острым углом [латекс] 34 [/ латекс] градуса и длиной гипотенузы [латекс] 25 [/ латекс] футов, найдите длину противоположной стороны.

Глядя на рисунок, решите для стороны, противоположной острому углу [латекса] 34 [/ латекса] градуса. Соотношение сторон будет равняться противоположной стороне и гипотенузе .{\ circ} [/ latex] и длина гипотенузы [latex] 300 [/ latex] футов, найдите длину гипотенузы (округлите до десятых):
Прямой треугольник: Для прямоугольного треугольника с острым углом [латекс] 83 [/ латекс] градуса и длиной гипотенузы [латекс] 300 [/ латекс] футов найдите длину гипотенузы.
Глядя на рисунок, решите гипотенузу острому углу [латекс] 83 [/ латекс] градуса. Соотношение сторон будет равняться смежной стороне и гипотенузе .{\ circ} \ right)}} \\ x & = \ frac {300} {\ left (0,1218 \ dots \ right)} \\ x & = 2461,7 ~ \ mathrm {feet} \ end {align}} [/ латекс]
Синус, косинус и тангенс
Мнемоника
SohCahToa может использоваться для определения длины стороны прямоугольного треугольника.
Цели обучения
Используйте аббревиатуру SohCahToa для определения синуса, косинуса и тангенса в терминах прямоугольных треугольников.
Основные выводы
Ключевые моменты
- Распространенный мнемоник для запоминания отношений между функциями синуса, косинуса и тангенса — SohCahToa.
- SohCahToa образован из первых букв « S ine is o pposite over h ypotenuse ( Soh ), C osine is a djacent over h ypotenuse ( h ypotenuse ), Касательная противоположна соседней ( Тоа ) ».
Определения тригонометрических функций
Для прямоугольного треугольника с острым углом [латекс] t [/ латекс] первые три тригонометрические функции:
- Синус [латекс] \ displaystyle {\ sin {t} = \ frac {напротив} {гипотенуза}} [/ латекс]
- Косинус [латекс] \ displaystyle {\ cos {t} = \ frac {соседний} {гипотенуза}} [/ латекс]
- Касательная [латекс] \ Displaystyle {\ tan {t} = \ frac {напротив} {смежный}} [/ латекс]
Распространенным мнемоническим символом для запоминания этих отношений является SohCahToa , образованный из первых букв « S In is o pposite over h ypotenuse ( Soh ), C acent osine is a .
 более ч гипотенуза ( Cah ), касательная противоположна соседней ( Тоа ).{\ circ} [/ latex] и прилегающую сторону [latex] 45 [/ latex] ножек, решите для длины противоположной стороны. (округляем до десятых)
более ч гипотенуза ( Cah ), касательная противоположна соседней ( Тоа ).{\ circ} [/ latex] и прилегающую сторону [latex] 45 [/ latex] ножек, решите для длины противоположной стороны. (округляем до десятых)Прямой треугольник: Дан прямоугольный треугольник с острым углом [латекс] 62 [/ латекс] градуса и прилегающей стороной [латекс] 45 [/ латекс] ступней, решите для длины противоположной стороны.
Во-первых, определите, какую тригонометрическую функцию использовать при заданной соседней стороне, и вам нужно найти противоположную сторону. Всегда определяйте, какая сторона дана, а какая неизвестна под острым углом ([латекс] 62 [/ латекс] градуса).\ circ [/ latex], гипотенуза составляет 30 футов, а длина отсутствующей стороны — это противоположная ножка, [latex] x [/ latex] футов.
Определите, какую тригонометрическую функцию использовать при заданной гипотенузе, и вам нужно найти противоположную сторону. Вспоминая мнемонику « S ohCahToa», указанные стороны представляют собой гипотенузу и противоположные «h» и «o», что означает использование «S» или тригонометрической функции синуса.
 {\ circ} \ right)} \\ x & = 30 \ cdot \ left (0.5299 \ dots \ right) \\ x & = 15.9 ~ \ mathrm {feet} \ end {align}} [/ latex]
{\ circ} \ right)} \\ x & = 30 \ cdot \ left (0.5299 \ dots \ right) \\ x & = 15.9 ~ \ mathrm {feet} \ end {align}} [/ latex]Определение углов из соотношений: обратные тригонометрические функции
Обратные тригонометрические функции можно использовать для определения острого угла прямоугольного треугольника.
Цели обучения
Использование обратных тригонометрических функций при решении задач с прямоугольными треугольниками
Основные выводы
Ключевые моменты
- Отсутствующее значение острого угла прямоугольного треугольника можно найти, если заданы две длины стороны.{-1} [/ латекс].
Использование тригонометрических функций для поиска отсутствующей стороны при заданном остром угле так же просто, как определение сторон относительно острого угла, выбор правильной функции, создание уравнения и решение. Так же просто найти недостающий острый угол при наличии двух сторон прямоугольного треугольника.
 {- 1} [/ latex] на калькуляторе), чтобы найти угол ([latex] A [/ latex]) с двух сторон.\ circ [/ latex] с противоположной длиной стороны [латекс] 12 ~ \ mathrm {feet} [/ latex], найдите острый угол с точностью до градуса:
{- 1} [/ latex] на калькуляторе), чтобы найти угол ([latex] A [/ latex]) с двух сторон.\ circ [/ latex] с противоположной длиной стороны [латекс] 12 ~ \ mathrm {feet} [/ latex], найдите острый угол с точностью до градуса:Прямой треугольник: Найдите угол [латекс] A [/ латекс], если задана противоположная сторона и гипотенуза.
От угла [латекс] А [/ латекс] даны стороны напротив и гипотенузы . Поэтому используйте тригонометрическую функцию синуса. ( Soh от SohCahToa) Напишите уравнение и решите его, используя обратный ключ для синуса.{\ circ} \ end {align}} [/ латекс]
Как найти угол в прямоугольном треугольнике
Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает одно
или другие ваши авторские права, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее
в
информацию, описанную ниже, назначенному ниже агенту. Если репетиторы университета предпримут действия в ответ на
Если репетиторы университета предпримут действия в ответ на
ан
Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент
средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как
в виде
ChillingEffects.org.Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатов), если вы существенно
искажать информацию о том, что продукт или действие нарушает ваши авторские права. Таким образом, если вы не уверены, что контент находится
на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.Чтобы отправить уведомление, выполните следующие действия:
Вы должны включить следующее:
Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени;
Идентификация авторских прав, которые, как утверждается, были нарушены;
Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \
достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например нам требуется
а
ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание
к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба;
д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; а также
Ваше заявление: (а) вы добросовестно полагаете, что использование контента, который, по вашему мнению, нарушает
ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы
либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.Отправьте жалобу нашему уполномоченному агенту по адресу:
Чарльз Кон
Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105Или заполните форму ниже:
Что такое прямой угол? — Определение и формула — Видео и стенограмма урока
Обозначение
Прямые углы имеют особые обозначения.
 Это символ, из-за которого кажется, что под углом находится маленький квадрат.Выглядит это так:
Это символ, из-за которого кажется, что под углом находится маленький квадрат.Выглядит это так:Маленькая квадратная рамка говорит вам, что это прямой угол.
Во многих местах вы увидите прямые углы. Вы увидите их в квадратах и прямоугольниках, где каждый угол представляет собой прямой угол. Одно из самых полезных мест, где вы их увидите, — это треугольники. Когда треугольник имеет прямой угол, он становится треугольником особого типа, называемым прямоугольным треугольником . У прямоугольных треугольников всегда ровно один угол, равный 90 градусам.Выглядят они так:
Правые треугольники служат основой для многих математических вещей, таких как определение расстояния вверх по склону, если вам известна только высота холма, и определение ширины холма. Без прямоугольных треугольников не было бы тригонометрии. Тригонометрические функции синуса, косинуса и тангенса основаны на прямоугольном треугольнике.

Теорема Пифагора
Одна из самых важных формул, с которыми вы когда-либо сталкивались в отношении прямоугольных треугольников, — это теорема Пифагора. Теорема Пифагора — это формула, которая связывает все три стороны прямоугольного треугольника друг с другом. Это позволяет вам найти одну сторону по двум другим.
Сторона c всегда гипотенуза или сторона, противоположная прямому углу. Гипотенуза — это всегда самая длинная сторона прямоугольного треугольника. Теорема Пифагора говорит вам, что квадрат гипотенузы такой же длины, как сумма квадратов двух других сторон.
Давайте посмотрим, как мы можем использовать теорему Пифагора, чтобы помочь нам решать проблемы. Допустим, у нас есть этот треугольник, и мы хотим найти недостающую сторону.
Недостающая сторона — это наша гипотенуза, поэтому мы можем обозначить эту сторону c .
 Сторона с цифрой 3 может быть помечена как a или b . Мы обозначим его и . Другая сторона — это b . Мы можем вставить нашу информацию в теорему Пифагора, чтобы найти недостающую сторону, вот так:
Сторона с цифрой 3 может быть помечена как a или b . Мы обозначим его и . Другая сторона — это b . Мы можем вставить нашу информацию в теорему Пифагора, чтобы найти недостающую сторону, вот так:Мы использовали свои навыки алгебры, чтобы выделить переменную x , найти ее и найти ответ.После прохождения процесса мы видим, что наша гипотенуза равна 5.
Если бы нам дали гипотенузу и одну из сторон и попросили найти другую сторону, что мы будем делать?
Начнем так же, как и раньше. Мы обозначаем 5 как c , потому что это гипотенуза. На 4-й стороне мы обозначим b , а на стороне x мы обозначим a . Затем мы вставляем нашу информацию в теорему Пифагора и решаем относительно x .
Мы все еще используем наши навыки алгебры, чтобы найти x .
 На этот раз нам пришлось переместить наш b на другую сторону путем вычитания. Наш ответ оказывается 3.
На этот раз нам пришлось переместить наш b на другую сторону путем вычитания. Наш ответ оказывается 3.Резюме урока
Прямые углы определяются как углы, которые составляют ровно 90 градусов. Самое важное место, где вы их увидите, — это треугольники. Формула, полученная из прямоугольного треугольника , является теоремой Пифагора , которая связывает все стороны прямоугольного треугольника друг с другом.Теорема Пифагора говорит вам, что квадрат гипотенузы такой же длины, как сумма квадратов двух других сторон.
Как найти углы прямоугольного треугольника
Обновлено 3 ноября 2020 г.
Крис Дезиел
Сложите значения трех углов в любом треугольнике, и вы получите 180 градусов. Если у вас прямоугольный треугольник, один из его углов по определению равен 90 градусам. Это означает, что сумма двух других углов должна составлять 90 градусов, и если вы знаете один из них, вы можете сразу найти другой.Но как найти углы, если вы тоже не знаете? Ответ заключается в том, чтобы полагаться на другое важное свойство треугольника — длину его сторон.
 Они связаны с величиной углов.
Они связаны с величиной углов.TL; DR (слишком длинный; не читал)
Найдите углы в прямоугольном треугольнике, вычислив их синус, косинус или тангенс, которые являются функциями длин сторон треугольника.
Синус, косинус и тангенс
Когда вы выбираете, какой из двух углов (ø) в прямоугольном треугольнике вы хотите найти, вы устанавливаете три стороны по отношению к нему.Линия, которая касается угла и продолжается до угла 90 градусов, называется стороной , прилегающей к углу , а сторона, противоположная углу, — стороной , противоположной стороне . Гипотенуза всегда находится на стороне, противоположной прямому углу. Основываясь на этих определениях, математики используют три соотношения, которые определяют угол в терминах длин сторон:
Синус (sin) — это отношение противоположной стороны к гипотенузе:
\ sin ø = \ frac {\ text {напротив}} {\ text {hypotenuse}}
Косинус (cos) — это отношение смежной стороны к гипотенузе:
\ cos ø = \ frac {\ text {смежный} } {\ text {hypotenuse}}
Касательная (загар) — это отношение противоположной стороны к соседней стороне:
\ tan ø = \ frac {\ text {напротив}} {\ text {смежный }}
Каждое отношение каждой пары линий соответствует определенному углу, и эти отношения сведены в таблицу вместе с углами, которые они определяют.
 Если вы можете измерить длину хотя бы двух сторон прямоугольного треугольника, все, что вам нужно сделать, это вычислить синус, косинус или тангенс угла и использовать таблицу, чтобы найти его.
Если вы можете измерить длину хотя бы двух сторон прямоугольного треугольника, все, что вам нужно сделать, это вычислить синус, косинус или тангенс угла и использовать таблицу, чтобы найти его.Лестница у стены
Одно из наиболее известных практических применений этих принципов — лестница, опирающаяся на вертикальную стену. Величины углов, которые лестница образует с землей и стеной, имеют решающее значение. Если угол относительно стены слишком мал, лестница упадет назад, а если угол на земле слишком мал, лестница соскользнет.Поскольку угол между стеной и землей составляет 90 градусов, вы можете рассчитать два угла, которые образует лестница, используя синус, косинус или тангенс, и таким образом вы можете предотвратить несчастный случай.
Лестница образует гипотенузу прямоугольного треугольника.
Это расстояние является соседней стороной при определении угла, под которым лестница образует с землей.
Используйте таблицы косинусов, чтобы найти угол между лестницей и землей.


 Прямой угол обозначается буквой d и равен 90°.
Прямой угол обозначается буквой d и равен 90°.
 Для начала, их следует высчитать математическим способом по уравнению корень квадратный из а2 + в2. Например, если стороны фундамента 8 и 10, диагональ будет равна 64 (8х8) + 100 (10х10) =»164, вычисляем корень из 164, получаем 12,8. Наша диагональ равна 12,8. У прямоугольников и квадратов диагонали равны.
Для начала, их следует высчитать математическим способом по уравнению корень квадратный из а2 + в2. Например, если стороны фундамента 8 и 10, диагональ будет равна 64 (8х8) + 100 (10х10) =»164, вычисляем корень из 164, получаем 12,8. Наша диагональ равна 12,8. У прямоугольников и квадратов диагонали равны. ..
.. 
 Выберите нужный вариант из раскрывающегося списка . Это третий.
Выберите нужный вариант из раскрывающегося списка . Это третий.
 Сторона [латекс] a [/ латекс] может быть идентифицирована как сторона, прилегающая к углу [латекс] B [/ латекс] и противоположная (или противоположная) углу [латекс] A [/ латекс].Сторона [латекс] b [/ латекс] — это сторона, прилегающая к уголку [латекс] A [/ латекс] и противоположная уголку [латекс] B [/ латекс].
Сторона [латекс] a [/ латекс] может быть идентифицирована как сторона, прилегающая к углу [латекс] B [/ латекс] и противоположная (или противоположная) углу [латекс] A [/ латекс].Сторона [латекс] b [/ латекс] — это сторона, прилегающая к уголку [латекс] A [/ латекс] и противоположная уголку [латекс] B [/ латекс].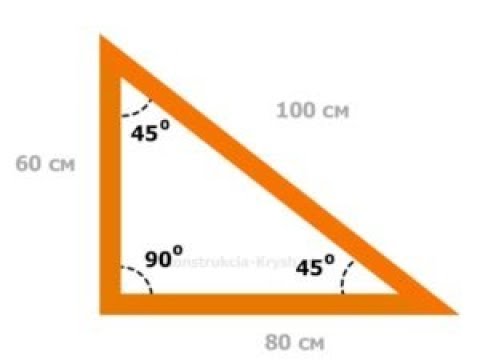
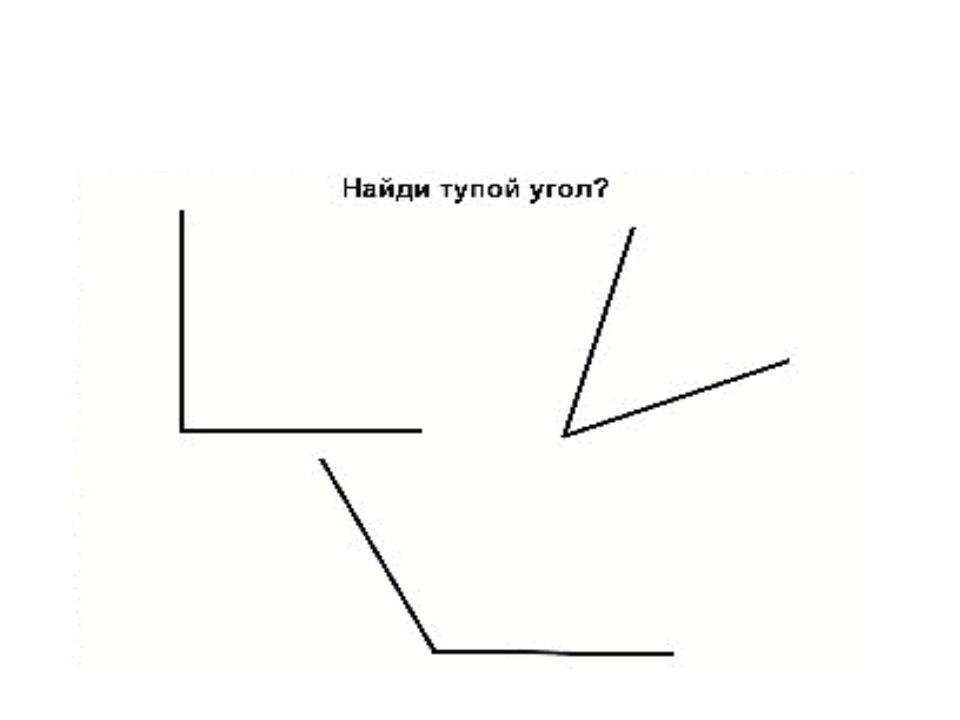 Соседняя сторона — это сторона, ближайшая к углу. («Соседний» означает «рядом».) Противоположная сторона — это сторона, противоположная углу. Гипотенуза — это сторона треугольника, противоположная прямому углу, и она самая длинная.
Соседняя сторона — это сторона, ближайшая к углу. («Соседний» означает «рядом».) Противоположная сторона — это сторона, противоположная углу. Гипотенуза — это сторона треугольника, противоположная прямому углу, и она самая длинная. При поиске отсутствующей стороны первым делом необходимо определить, какие стороны и под каким углом даны, а затем выбрать соответствующую функцию, которая будет использоваться для решения проблемы.
При поиске отсутствующей стороны первым делом необходимо определить, какие стороны и под каким углом даны, а затем выбрать соответствующую функцию, которая будет использоваться для решения проблемы.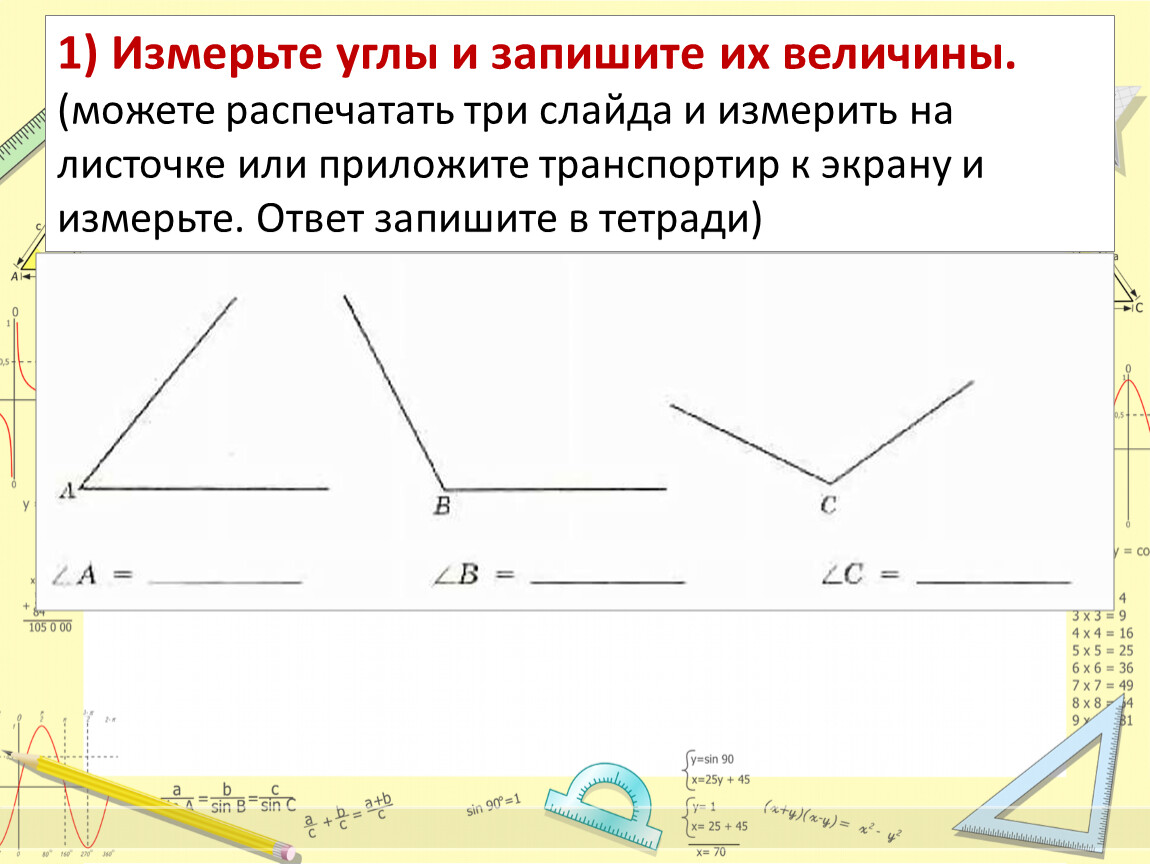
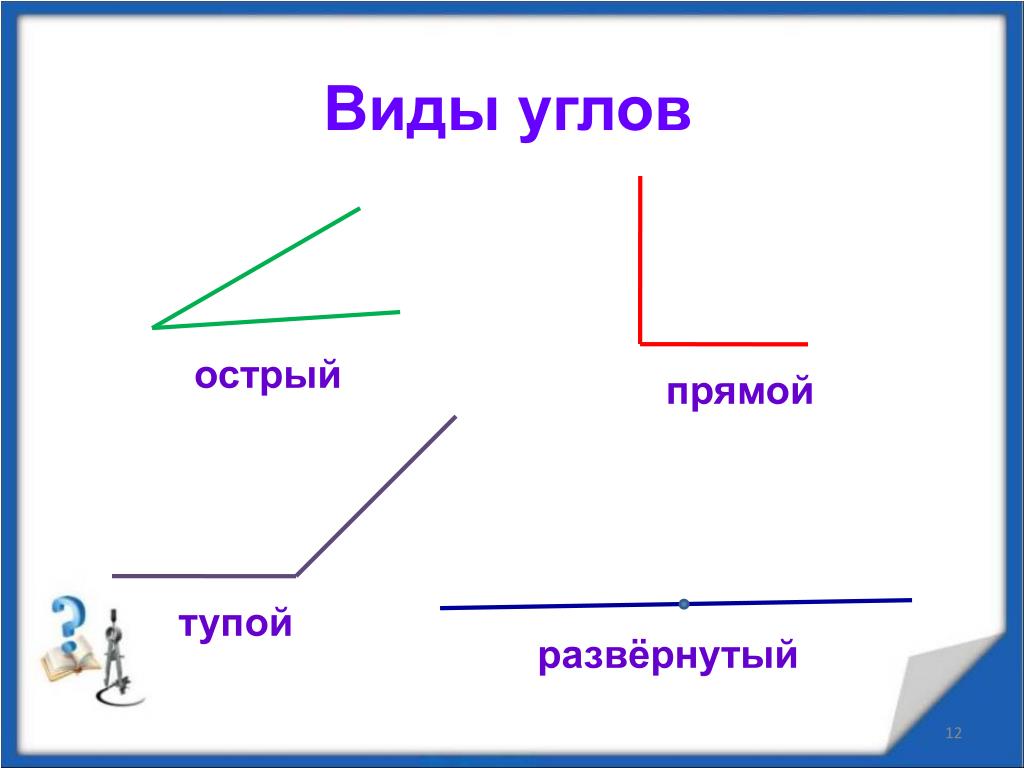
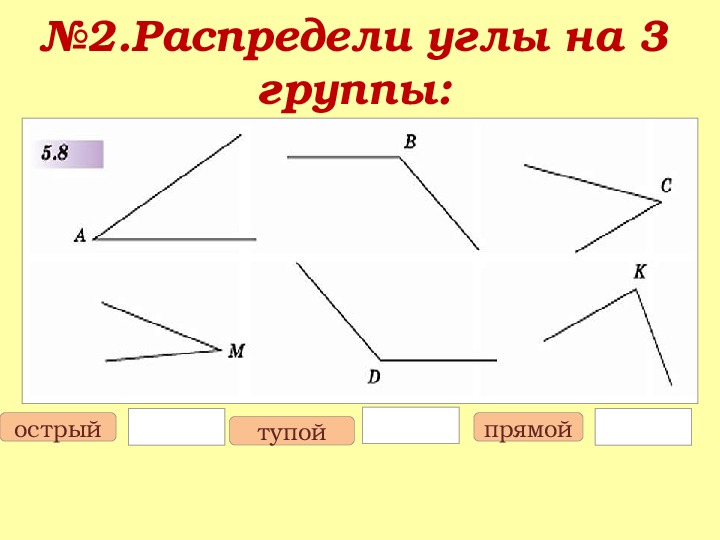 более ч гипотенуза ( Cah ), касательная противоположна соседней ( Тоа ).{\ circ} [/ latex] и прилегающую сторону [latex] 45 [/ latex] ножек, решите для длины противоположной стороны. (округляем до десятых)
более ч гипотенуза ( Cah ), касательная противоположна соседней ( Тоа ).{\ circ} [/ latex] и прилегающую сторону [latex] 45 [/ latex] ножек, решите для длины противоположной стороны. (округляем до десятых)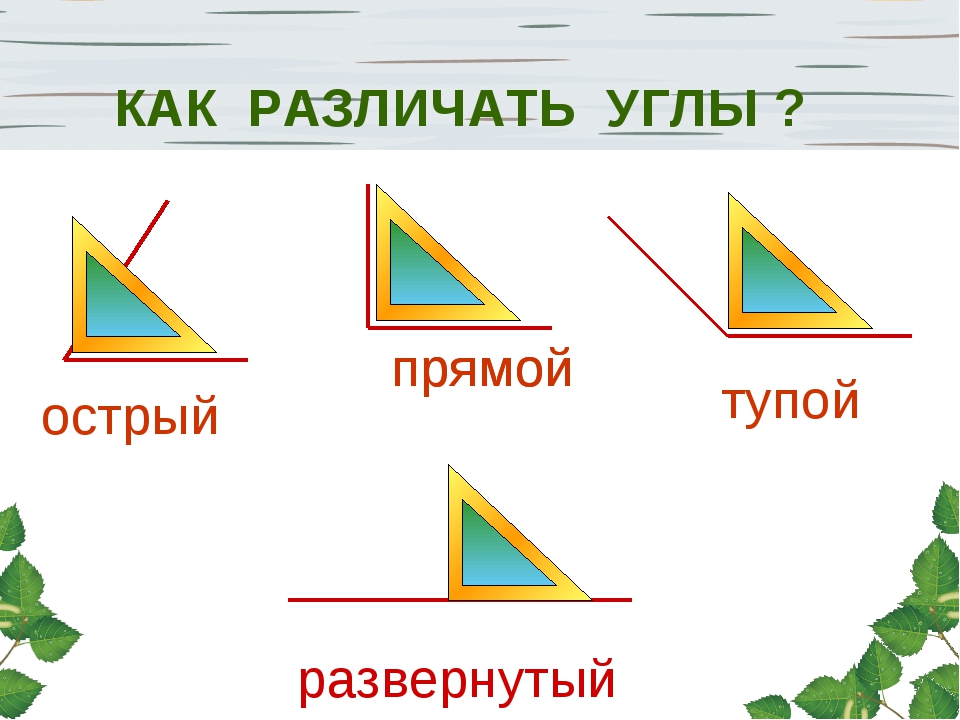 {\ circ} \ right)} \\ x & = 30 \ cdot \ left (0.5299 \ dots \ right) \\ x & = 15.9 ~ \ mathrm {feet} \ end {align}} [/ latex]
{\ circ} \ right)} \\ x & = 30 \ cdot \ left (0.5299 \ dots \ right) \\ x & = 15.9 ~ \ mathrm {feet} \ end {align}} [/ latex]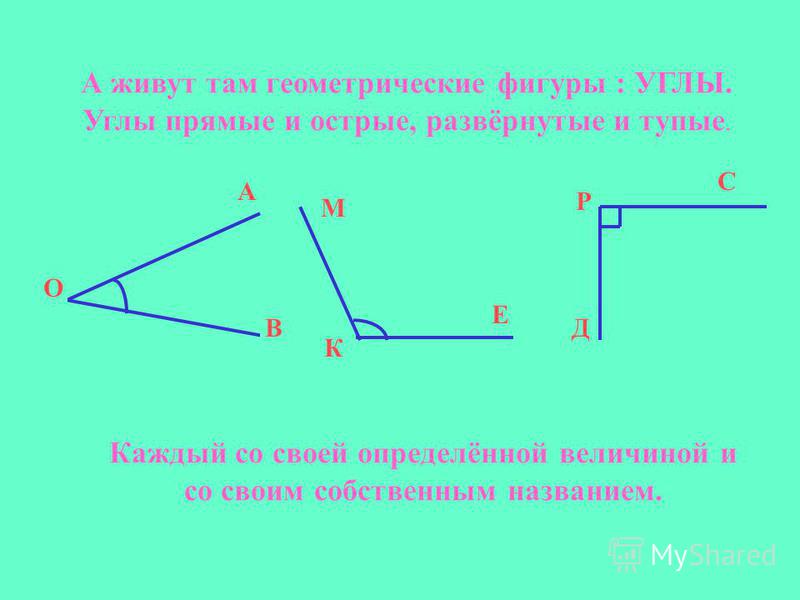 {- 1} [/ latex] на калькуляторе), чтобы найти угол ([latex] A [/ latex]) с двух сторон.\ circ [/ latex] с противоположной длиной стороны [латекс] 12 ~ \ mathrm {feet} [/ latex], найдите острый угол с точностью до градуса:
{- 1} [/ latex] на калькуляторе), чтобы найти угол ([latex] A [/ latex]) с двух сторон.\ circ [/ latex] с противоположной длиной стороны [латекс] 12 ~ \ mathrm {feet} [/ latex], найдите острый угол с точностью до градуса: Если репетиторы университета предпримут действия в ответ на
Если репетиторы университета предпримут действия в ответ на д. — относится ваша жалоба;
д. — относится ваша жалоба;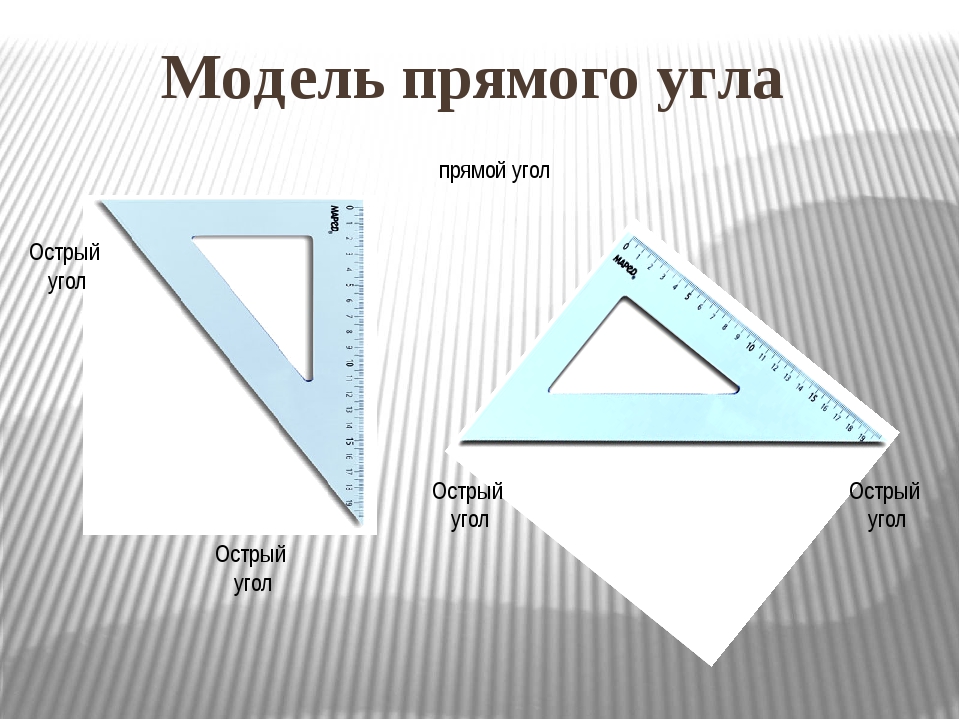 Это символ, из-за которого кажется, что под углом находится маленький квадрат.Выглядит это так:
Это символ, из-за которого кажется, что под углом находится маленький квадрат.Выглядит это так: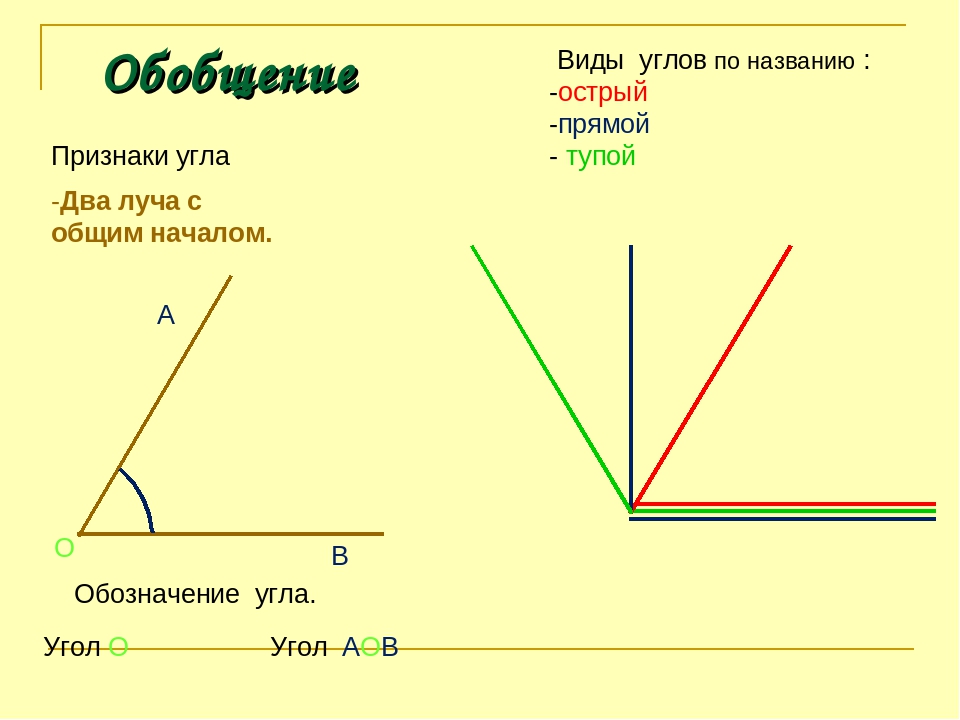
 Сторона с цифрой 3 может быть помечена как a или b . Мы обозначим его и . Другая сторона — это b . Мы можем вставить нашу информацию в теорему Пифагора, чтобы найти недостающую сторону, вот так:
Сторона с цифрой 3 может быть помечена как a или b . Мы обозначим его и . Другая сторона — это b . Мы можем вставить нашу информацию в теорему Пифагора, чтобы найти недостающую сторону, вот так: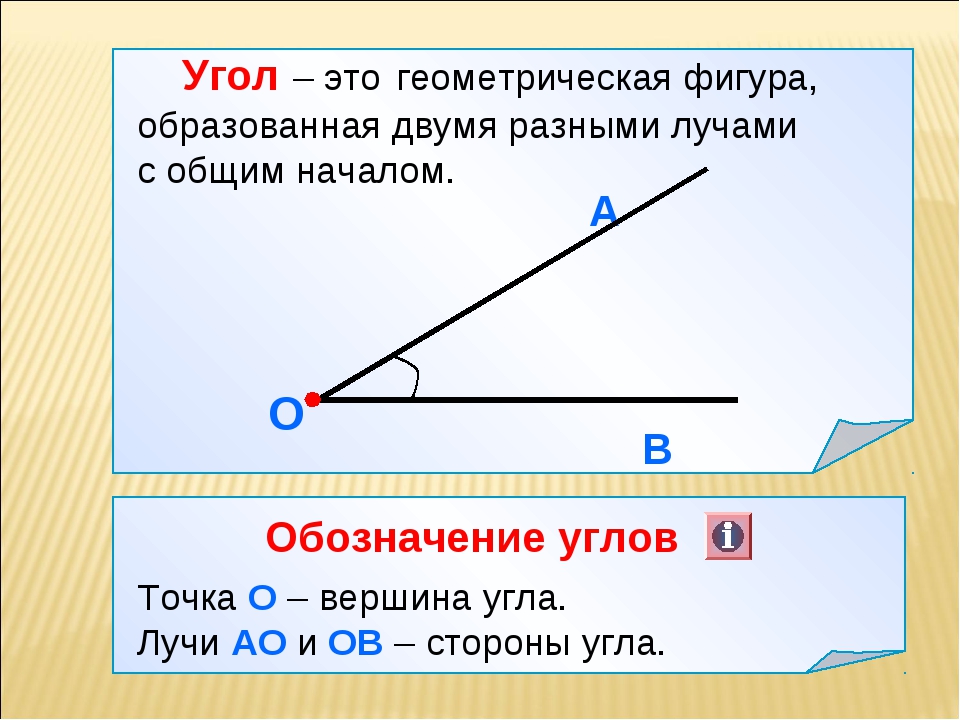 На этот раз нам пришлось переместить наш b на другую сторону путем вычитания. Наш ответ оказывается 3.
На этот раз нам пришлось переместить наш b на другую сторону путем вычитания. Наш ответ оказывается 3.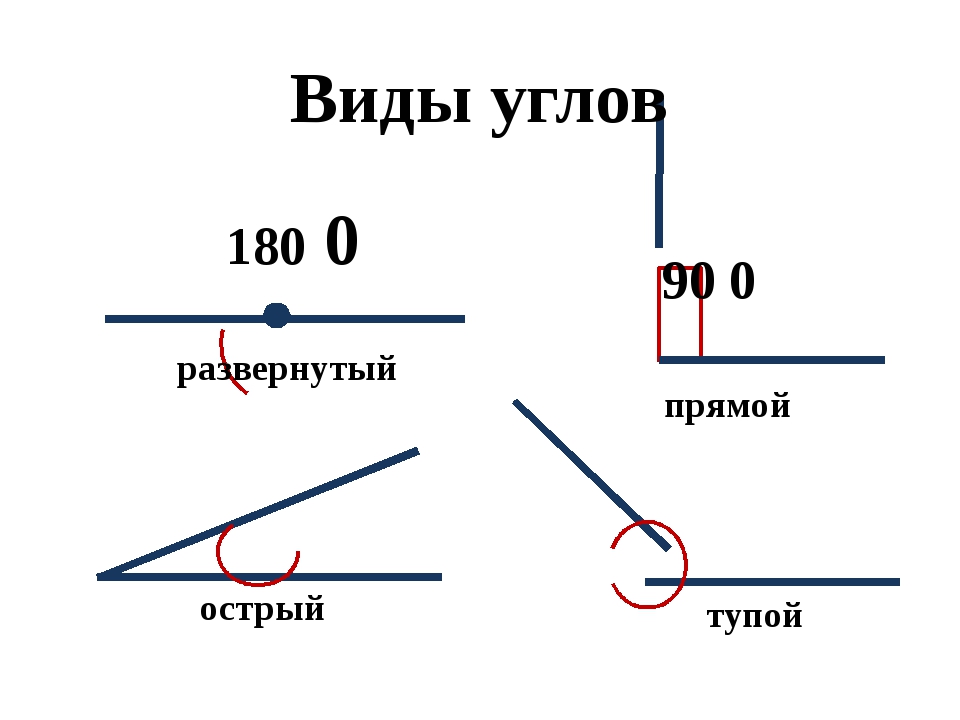 Они связаны с величиной углов.
Они связаны с величиной углов.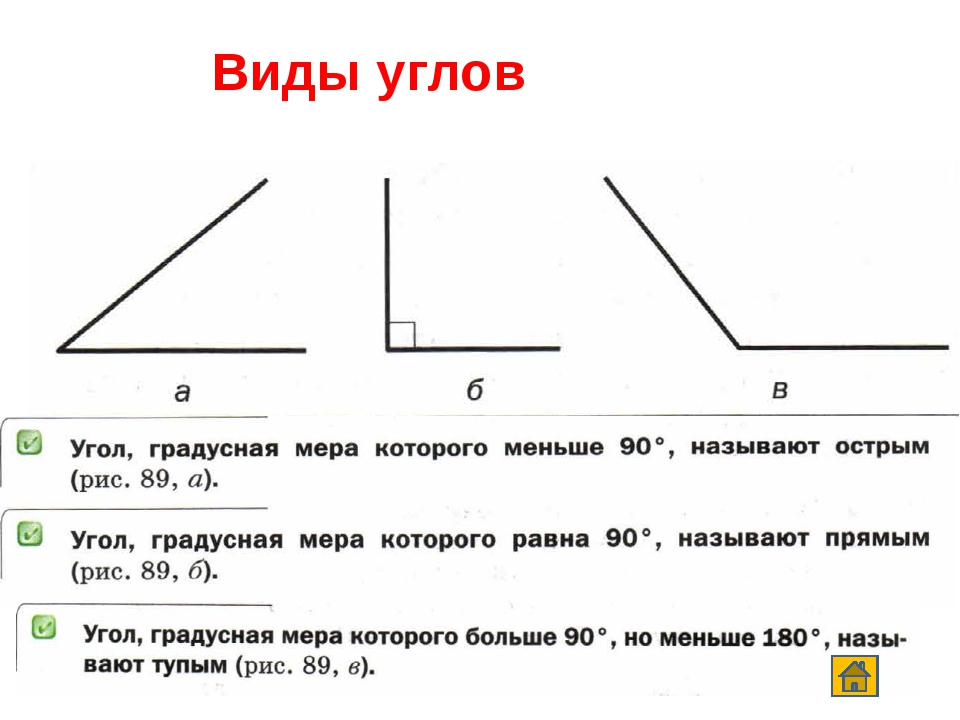 Если вы можете измерить длину хотя бы двух сторон прямоугольного треугольника, все, что вам нужно сделать, это вычислить синус, косинус или тангенс угла и использовать таблицу, чтобы найти его.
Если вы можете измерить длину хотя бы двух сторон прямоугольного треугольника, все, что вам нужно сделать, это вычислить синус, косинус или тангенс угла и использовать таблицу, чтобы найти его.