Как узнать угол прямой: Найти угол наклона прямой онлайн

Коэффициент наклона прямой

Что такое линейная функция и как выглядит ее график мы подробно разбирали здесь.

В этой статье мы остановимся на том, как находить коэффициент наклона прямой.

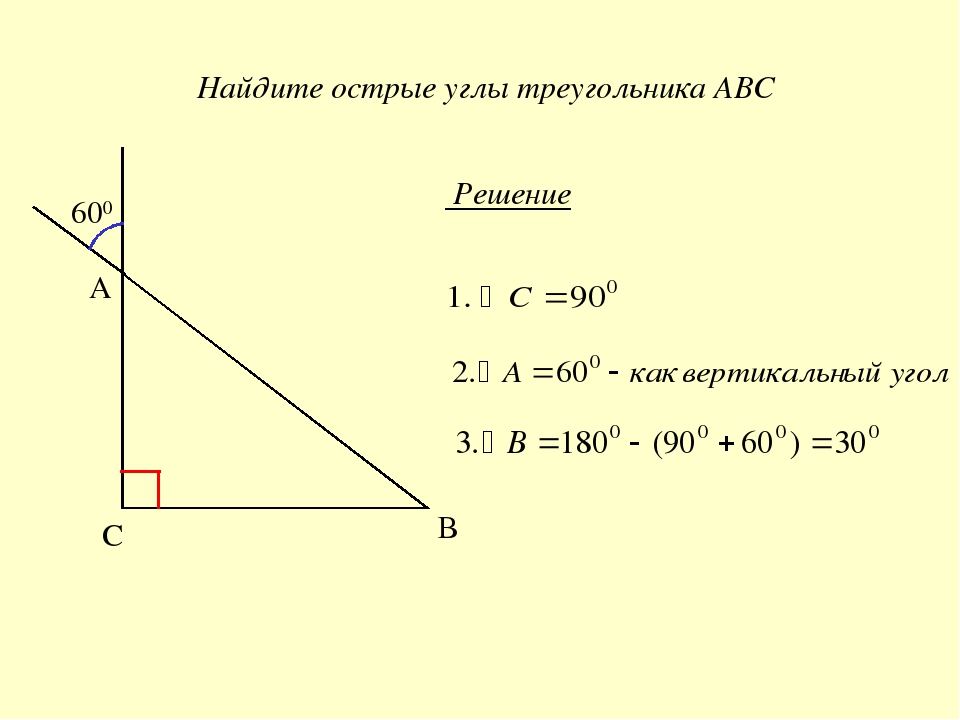
Как мы знаем, уравнение прямой имеет вид . В этом уравнении коэффициент при отвечает за наклон прямой и называется коэффициентом наклона. Он равен тангенсу угла между прямой и положительным направлением оси .

Внимание! Не просто между прямой и осью , а именно между прямой и положительным направлением оси .

Например, в прямой коэффициент наклона равен , в прямой  коэффициент наклона равен .

В уравнении прямой  слагаемое, содержащее отсутствует, следовательно, коэффициент при  равен нулю. Угол наклона этой прямой к оси  равен нулю — прямая  параллельна оси .

Если прямая наклонена вправо, то угол между прямой и положительным направлением оси — острый, соответственно, тангенс этого угла больше нуля, и коэффициент .

Например:

Здесь

Если прямая наклонена влево, то угол между прямой и положительным направлением оси — тупой, соответственно, тангенс этого угла меньше нуля, и коэффициент :

Здесь .

Решим две задачи на нахождение коэффициента наклона прямой.

1. Най­ди­те уг­ло­вой ко­эф­фи­ци­ент пря­мой, про­хо­дя­щей через точки с ко­ор­ди­на­та­ми (-1;-1) и (1;3).

Решим эту задачу  двумя способами.

А). Так как прямая проходит через точки (-1;-1) и (1;3), координаты этих точек удовлетворяют уравнению прямой . То есть если мы координаты каждой точки подставим в уравнение прямой, то получим верное равенство. Так как у нас две точки, получаем систему:

или

Вычтем из второго уравнения первое, и получим , отсюда .

Б). Построим график этой функции. Для этого нанесем данные точки А(-1;-1) и В(1;3) на координатную плоскость и проведем через них прямую:

Коэффициент равен тангенсу угла наклона между прямой и положительным направлением оси , на чертеже это угол :

Чтобы найти рассмотрим прямоугольный треугольник АВС с вершинами в данных точках.

Угол прямоугольного треугольника АВС равен углу (соответственные углы, полученный при пересечении параллельных прямых АС и ОХ секущей АВ):

равен отношению противолежащего катета к прилежащему, то есть

Отсюда

2. Най­ди­те уг­ло­вой ко­эф­фи­ци­ент пря­мой, про­хо­дя­щей через точки с ко­ор­ди­на­та­ми (4;0) и (0;8).

Решение с помощью системы уравнений абсолютно аналогично решению предыдущей задачи, можете воспроизвести его самостоятельно.

Выполним это задание с помощью графика.

Нанесем данные токи на координатную плоскость и проведем через них прямую:

Угол между прямой и положительным направлением оси ОХ — это угол :

Коэффициент наклона прямой  . Чтобы найти , построим прямоугольный треугольник ВОА: 

В этом прямоугольном треугольнике угол    — внешний. Мы можем найти тангенс внутреннего угла  .  .

. Отсюда  .

Еще раз! Если прямая наклонена влево, то коэффициент наклона прямой отрицательный.

И.В. Фельдман, репетитор по математике.

Угловой коэффициент прямой

  Угловой коэффициент прямой. В этой статье мы с вами рассмотрим задачи связанные с координатной плоскостью включённые в ЕГЭ по математике. Это задания на:

— определение углового коэффициента прямой, когда известны две точки через которые она проходит;
— определение абсциссы или ординаты точки пересечения двух прямых на плоскости.

Что такое абсцисса и ордината точки было описано в прошлой статье данной рубрики. В ней мы уже рассмотрели несколько задач связанных с координатной плоскостью. Что необходимо понимать для рассматриваемого типа задач? Немного теории.

Уравнение прямой на координатной плоскости имеет вид:

где k – это и есть угловой коэффициент прямой.

Следующий момент! Угловой коэффициент прямой равен тангенсу угла наклона прямой. Это угол между данной прямой и осью ох.

Он лежит в пределах от 0 до 180 градусов.

То есть, если мы приведём уравнение прямой к виду y = kx + b, то далее всегда сможем определить коэффициент k (угловой коэффициент).

Так же, если мы исходя из условия сможем определить тангенс угла наклона прямой, то тем самым найдём её угловой коэффициент.

Следующий теоретический момент! Уравнение прямой походящей через две данные точки. Формула имеет вид:

Подробнее об этой формуле рассказано в этой статье!

Рассмотрим задачи (аналогичные задачам из открытого банка заданий):

Найдите угловой коэффициент прямой, проходящей через точки с координатами (–6;0) и (0;6).

В данной задаче самый рациональный путь решения это найти тангенс угла между осью ох и данной прямой. Известно, что он равен угловому коэффициенту. Рассмотрим прямоугольный треугольник образованный прямой и осями ох и оу:

Тангенсом угла в прямоугольном треугольнике является отношение противолежащего катета к прилежащему:

*Оба катета равны шести (это их длины).

Конечно, данную задачу можно решить используя формулу нахождения уравнения прямой проходящей через две данные точки. Но это будет более длительный путь решения.

Ответ: 1

Найдите угловой коэффициент прямой, проходящей через точки с координатами (5;0) и (0;5).

Формула уравнения прямой походящей через две данные точки имеет вид:

Наши точки  имеют координаты (5;0) и (0;5). Значит,

Приведём формулу к виду  y = kx + b   

Получили, что угловой коэффициент  k = – 1.

Ответ: –1

Прямая a проходит через точки с координатами (0;6) и (8;0). Прямая b проходит через точку с координатами (0;10) и параллельна прямой a. Найдите абсциссу точки пересечения прямой b с осью оx.

В данной задаче можно найти уравнение прямой a, определить угловой коэффициент для неё. У прямой b угловой коэффициент будет такой же, так как они параллельны. Далее можно найти уравнение прямой b. А затем, подставив в него значение y = 0, найти абсциссу. НО!

В данном случае, проще использовать свойство подобия треугольников.

Прямоугольные треугольники, образованные данными (параллельными) прямыми о осями координат подобны, а это значит, что отношения их соответствующих сторон равны.

Искомая абсцисса равна 40/3.

Ответ: 40/3

Прямая a проходит через точки с координатами (0;8) и (–12;0). Прямая b проходит через точку с координатами (0; –12) и параллельна прямой a. Найдите абсциссу точки пересечения прямой b с осью оx.

Для данной задачи самый рациональный путь решения — это применение свойства подобия треугольников. Но мы решим её другим путём.

Нам известны точки, через которые проходит прямая а. Можем составить уравнение прямой. Формула уравнения прямой походящей через две данные точки имеет вид:

По условию точки  имеют координаты (0;8) и (–12;0). Значит,

Приведём к виду   y = kx + b:

Получили, что угловой  k = 2/3.

*Угловой коэффициент можно было найти через тангенс угла в прямоугольном треугольнике с катетами 8 и 12.

Известно, у параллельных прямых угловые коэффициенты равны. Значит уравнение прямой проходящей через точку (0;-12) имеет вид:

Найти величину b  мы можем подставив абсциссу и ординату в уравнение:

Таким образом, прямая имеет вид:

Теперь чтобы найти искомую абсциссу точки пересечения прямой с осью ох, необходимо подставить у = 0:

Ответ: 18

Найдите ординату точки пересечения оси оy и прямой, проходящей через точку В(10;12) и параллельной прямой, проходящей через начало координат и точку А(10;24).

Найдём уравнение прямой проходящей через точки с координатами (0;0) и (10;24).

Формула уравнения прямой походящей через две данные точки имеет вид:

Наши точки  имеют координаты (0;0) и (10;24). Значит,

Приведём к виду   y = kx + b   

Угловые коэффициенты параллельных прямых равны. Значит, уравнение прямой, проходящей через точку В(10;12) имеет вид:

Значение b  найдём подставив в это уравнение координаты точки В(10;12):

Получили уравнение прямой:

Чтобы найти ординату точки пересечения этой прямой с осью оу  нужно подставить в найденное уравнение х = 0:

*Самый простой способ решения. При помощи параллельного  переноса сдвигаем данную прямую вниз вдоль оси оу до точки (10;12). Сдвиг происходит на 12 единиц, то есть точка А(10;24) «перешла» в точку В(10;12), а точка О(0;0) «перешла» в точку (0;–12). Значит, полученная прямая будет пересекать ось оу в точке (0;–12).

Искомая ордината равна  –12.

Ответ: –12

Найдите ординату точки пересечения прямой, заданной уравнением 

3х + 2у = 6, с осью Oy.

Координата точки пересечения заданной прямой с осью оу имеет вид (0;у). Подставим в уравнение абсциссу х = 0, и найдём ординату:

Ордината  точки пересечения прямой с осью оу равна 3.

*Решается система:

Ответ: 3

Найдите ординату точки пересечения прямых, заданных уравнениями 

3х + 2у = 6   и  у = – х.

Когда заданны две прямые, и стоит вопрос о нахождении координат точки пересечения этих прямых, решается система из данных уравнений:

В первом уравнении подставляем    – х   вместо у:

Ордината равна минус шести.

Ответ: – 6

Найдите угловой коэффициент прямой, проходящей через точки с координатами (–2;0) и (0;2).

Посмотреть решение

Найдите угловой коэффициент прямой, проходящей через точки с координатами (2;0) и (0;2).

Посмотреть решение

Прямая a проходит через точки с координатами (0;4) и (6;0). Прямая b проходит через точку с координатами (0;8) и параллельна прямой a. Найдите абсциссу точки пересечения прямой b с осью Ox.

Посмотреть решение

Прямая a проходит через точки с координатами (0;4) и (–6;0). Прямая b проходит через точку с координатами (0; –6) и параллельна прямой a. Найдите абсциссу точки пересечения прямой b с осью Ox.

Посмотреть решение

Найдите ординату точки пересечения оси оy и прямой, проходящей через точку B (6;4) и параллельной прямой, проходящей через начало координат и точку A (6;8).

Посмотреть решение

Найдите абсциссу точки пересечения прямой, заданной уравнением 2х + 2у = 6, с осью ох.

Посмотреть решение

Найдите абсциссу точки пересечения прямых, заданных уравнениями 3х + 2у = 6  и у = х.

Посмотреть решение

Конечно, некоторые задачи, которые мы рассмотрели можно было решить более рациональными способами. Но ставилась цель показать разные подходы к решению. Надеюсь, это удалось.

1. Необходимо чётко усвоить, что угловой коэффициент прямой равен тангенсу угла наклона прямой. Это поможет вам при решении многих задач данного типа.

2. Формулу нахождения прямой проходящей через две данные точки нужно понимать обязательно. С её помощью всегда найдёте уравнение прямой, если даны координаты двух её точек.

3. Помните о том, что угловые коэффициенты параллельных прямых равны.

4. Как вы поняли, в некоторых задачах удобно использовать признак подобия треугольников. Задачи решаются практически устно.

5. Задачи в которых даны две прямые и требуется найти абсциссу или ординату точки их пересечения можно решить графическим способом. То есть, построить их на координатной плоскости (на листе в клетку) и определить точку пересечения визуально. *Но этот способ применим не всегда.

6. И последнее. Если дана прямая и координаты точек её пересечения с осями координат, то в таких задачах удобно находить угловой коэффициент через нахождение тангенса угла в образованном прямоугольном треугольнике. Как «увидеть» этот треугольник при различных расположениях прямых на плоскости схематично показано ниже:

>> Угол наклона прямой от 0 до 90 градусов <<

>> Угол наклона прямой от 90 до 180 градусов <<

В данных двух случаях, по свойству тангенса:

То есть, чтобы найти уголвой коэффициент прямой, необходимо вычислить тангенс бетта в полученном прямоугольном треугольнике и записать результат с отрицательным знаком.

В данной рубрике продолжим рассматривать задачи, не пропустите!

На этом всё. Успеха Вам!

С уважением, Александр.

P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.

прямоугольных треугольников

прямоугольных треугольников

Давайте снова согласимся со стандартным правилом обозначения частей прямоугольного треугольника. Пусть прямой угол обозначен C , а гипотенуза c. Пусть A и B обозначают два других угла, а a и b стороны, противоположные им соответственно.

Решение прямоугольных треугольников

Мы можем использовать теорему Пифагора и свойства синусов, косинусов и тангенсов для решения треугольника, то есть для нахождения неизвестных частей через известные части.

• Теорема Пифагора:   a ²  +  b ²  =  c ² .
• Синусы: sin A = a/c, sin B  = b/c.
• Косинусы:   cos  A  =  b/c, cos  B  =  a/c.
• Касательные: tan A = a/b, tan B  = b/a.

Давайте сначала рассмотрим некоторые случаи, когда мы не знаем всех сторон. Предположим, мы не знаем гипотенузу, но знаем две другие стороны. Теорема Пифагора даст нам гипотенузу. Например, если a  = 10 и b  = 24, затем c ²  =  a ²  +  b ²  = 10  ²  + 24  ²  = 100 + 576 = 676. Квадратный корень из 676 равен 26, поэтому c  = 26. (Приятно привести примеры, когда из квадратных корней получаются целые числа; в жизни это обычно не так.)

Теперь предположим, что мы знаем гипотенузу и одну сторону, но должны найти другую. Например, если b  = 119 и c  = 169, затем a ²  = c ²  –  b ²  = 169 9002 4 2  – 119  ²  = 28 561 – 14 161 = 14 400, и квадратный корень из 14 400 равно 120, поэтому a  = 120.

Мы можем знать только одну сторону, но мы также знаем угол. Например, если сторона a  = 15 и угол A  = 41°, мы можем использовать синус и тангенс, чтобы найти гипотенузу и другую сторону. Поскольку грех A  = a/c, мы знаем c  = a /sin A  = 15/sin 41. Используя калькулятор, это 15/0,6561 = 22,864. Кроме того, tan A = a/b, , поэтому b = a /tan A = 15/tan 41 = 15/0,8693 = 17,256. Используете ли вы синус, косинус или тангенс, зависит от того, какую сторону и угол вы знаете.

Обратные триггерные функции: арксинус, арккосинус и арктангенс

Теперь давайте рассмотрим задачу нахождения углов, если известны стороны. Опять же, вы используете триггерные функции, но наоборот. Вот пример. Предположим a  = 12,3 и b  = 50,1. Тогда тангенс A = a/b = 12,3/50,1 = 0,2455. Раньше, когда люди использовали таблицы триггерных функций, они просто смотрели в таблицу тангенсов, чтобы увидеть, какой угол имеет тангенс 0,2455. На калькуляторе мы используем обратные триггерные функции, называемые арктангенс, арксинус и арккосинус. Обычно на калькуляторе есть кнопка с надписью «inv» или «arc», которую вы нажимаете перед нажатием соответствующей кнопки триггера.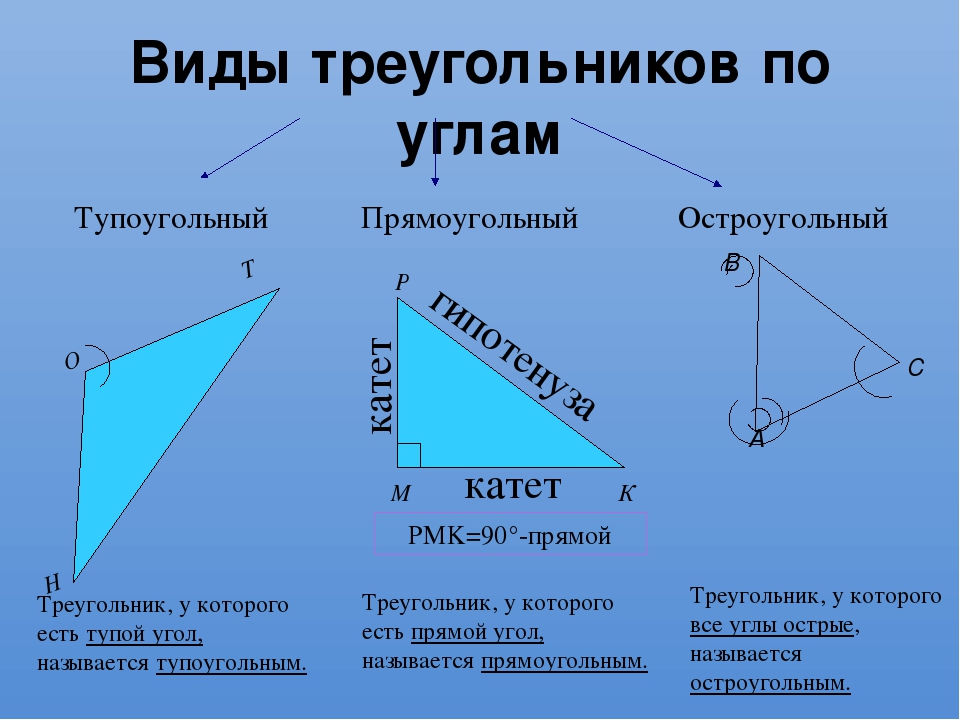 Арктангенс 0,2455 равен 13,79., поэтому угол A равен 13,79°. (Если хотите, вы можете преобразовать 0,79 градуса в минуты и секунды.)

Вот и все.

Остальные три тригонометрические функции: котангенс, секанс и косеканс

Для большинства целей достаточно трех триггерных функций: синуса, косинуса и тангенса. Однако бывают случаи, когда нужны какие-то другие. В исчислении часто используется секанс. Вы можете спросить: «Почему шесть триггерных функций?» Это своего рода симметрия. Есть шесть способов сделать отношения двух сторон прямоугольного треугольника, и это дает шесть функций:

1. sin  A  =  a/c (opp/hyp)
2. cos  A  =  b/c (adj/hyp)
3. tan  A  =  a/b (opp/adj)
4. детская кроватка A  =  b/a (adj/opp)
5. сек  A  =  c/b (hyp/adj)
6. csc  A  =  c/a (hyp/opp)

Из листинга видно, что котангенс (сокращенно cot или иногда ctn) является величиной, обратной величине тангенса, секанс (сокращенно sec) является величиной, обратной величине косинуса, а косеканс (сокращенно csc или иногда cosec) является величиной, обратной величине синуса. Они в значительной степени избыточны, но стоит знать, что они собой представляют на случай, если вы столкнетесь с ними. Обратите внимание, что котангенсы являются тангенсами дополнительных углов, а это означает, что cot A  = tan B, и косекансы являются секущими дополнительных углов, а это означает, что csc A  = sec  B.

Эти три другие функции также можно интерпретировать с помощью единичной круговой диаграммы.

Мы рассматриваем угол AOB. Напомним, что его касательной является прямая AC. По симметрии тангенсом угла FOB является прямая FG, но FOB является дополнительным углом AOB, , следовательно, котангенс AOB равен FG.

Далее, интерпретировать секущие геометрически. Угол AOB появляется в треугольнике COA как угол AOC, so sec  AOB  = sec  AOC  = hyp/adj =  OC/OA  =  ОС. Итак, секанс — это линия, проведенная из центра круга к касательной AC. Причина, по которой его называют секущим, заключается в том, что он пересекает круг, а слово «секанс» происходит от латинского слова, означающего «разрезание».

Аналогично, косекансом угла AOB является прямая OG , проведенная из центра окружности к прямой FG котангенса.

Упражнения

Примечание: как обычно, во всех упражнениях на прямоугольные треугольники c обозначают гипотенузу, a и b перпендикулярные стороны, A и B углы, противоположные a и б соответственно.

26. В каждом из следующих прямоугольных треугольников, две стороны которых заданы, вычислите sin, cos и тангенс углов A и B. Выразите результаты в виде обыкновенных дробей.

(и). c  = 41, a  = 9.

(ii). c  = 37, a  = 35.

(iii). a  = 24, b  = 7.

31. В прямоугольном треугольнике c  = 6 футов 3 дюйма и tan  В  = 1,2. Найдите a и b.

34. a  = 1,2, b  = 2,3. Найти A и c.

42. a  = 10,11, b  = 5,14. Найти B и c.

В следующих нескольких задачах треугольники не являются прямоугольными, но вы можете решить их, используя свои знания о прямоугольных треугольниках.

61. В косом треугольнике ABC, A  = 30°, B  = 45°, а перпендикуляр из C на AB равен 12 дюймов в длину. Найдите длину АВ.

67. Если сторона равностороннего треугольника равна а, найти высоту и радиусы описанной и вписанной окружностей.

202. От вершины здания высотой 50 футов углы возвышения и углубления вершины и низа другого здания равны 19° 41′ и 26° 34′ соответственно. Каковы высота и расстояние до второго здания.

207. С вершины маяка высотой 175 футов углы наклона вершины и низа флагштока составляют 23° 17′ и 42° 38′ соответственно. Какой высоты столб?

214. В двух точках на расстоянии 65 футов друг от друга на одной стороне дерева и на одной линии с ним углы возвышения вершины дерева составляют 21° 19′ и 16° 20′. Найдите высоту дерева.

215. Когда воздушный шар проходит между двумя точками A, и B, находящимися на расстоянии 2 миль друг от друга, углы места воздушного шара в этих точках составляют 27° 19′ и 41° 45′ соответственно. Найдите высоту воздушного шара. Возьмите A и B одного уровня.

233. Верхняя часть маяка находится на высоте 230 футов над уровнем моря. Как далеко находится объект, который находится «на горизонте»? [Предположим, что Земля представляет собой сферу радиусом 3956 миль.]

234. На какой высоте должен находиться наблюдатель, чтобы он мог видеть объект на Земле на расстоянии тридцати миль? Предположим, что Земля представляет собой гладкий шар.

В каждой из фигур, названных в следующих нескольких задачах, объект должен выразить свою площадь (i) через радиус R, , то есть радиус описанной окружности, (ii) через апофема r, то есть радиус вписанной окружности, и (iii) по стороне а.

251. Равносторонний треугольник. [См. задачу 67 выше.]

252. Квадрат.

253. Правильный пятиугольник.

254. Правильный шестигранник.

255. Правильный восьмиугольник.

Советы

26. Вам нужны только sin, cos и тангенс углов A и B ; вам не нужны сами углы. Таким образом, вам нужна только третья сторона, которую вы можете вычислить с помощью теоремы Пифагора, а затем взять отношения двух сторон.

31. Вы знаете c и tan B. К сожалению, tan B — это отношение двух неизвестных вам сторон, а именно b/a. Существует несколько способов решения этой проблемы. Вот два.

Метод 1. Возьмем уравнение 1.2 = tan  B  =  b/a, , чтобы получить соотношение между a и b, , а именно b  = 1,2 a . Теорема Пифагора тогда дает 6,25 ² = a ² + 1,44 a ² , из которых можно определить a, и затем найти b.

Способ 2. Из тангенса B, можно определить угол B (используйте арктангенс). Отсюда вы можете найти cos B, , а затем a, , и вы можете найти sin B, , а затем b.

34. Поскольку у вас есть a и b, вы можете использовать тангенсы, чтобы найти A и теорему Пифагора, чтобы найти c.

42. Найдите B по касательной и c по теореме Пифагора.

61. Начните с рисования фигуры. Хотя треугольник ABC не является прямоугольным, он распадается на два прямоугольных треугольника. Вы можете использовать касательные, чтобы найти две части стороны AB и сложить их вместе.

67. Равносторонний треугольник ABC имеет три угла при вершине по 60°. Отбросьте перпендикуляр из одной вершины, скажем, вершины C, , и вы получите два конгруэнтных прямоугольных треугольника ACF и BCF, , и вы можете найти длину этого перпендикуляра, а это высота равностороннего треугольника. Описанная окружность — это та, которая проходит через три вершины, а вписанная окружность — это та, которая касается внутри трех сторон. Отбрасывая перпендикуляры из другой вершины равностороннего треугольника и применяя тригонометрию к полученным маленьким треугольникам, можно найти радиусы этих двух окружностей.

202. Поскольку вы знаете высоту своего здания и угол наклона к основанию другого здания, вы можете определить, как далеко оно находится. Тогда угол подъема на вершину другого здания скажет вам, насколько оно выше вашего.

207. Подсказка похожа на 202. Смотрите, триггер может быть полезен, если вы одинокий смотритель маяка и не знаете, что делать!

214. Это полезная задача. Вы можете использовать его, чтобы найти высоты недоступных вещей. Нарисуйте фигуру. Есть два неизвестных: высота х дерева и расстояние х ближайшей точки к дереву. Дальнейшая точка — 90 003 x 90 004 + 65 футов от дерева. Используя тангенсы известных углов, вы можете составить два уравнения, которые можно решить для определения y и x.

215. Это похоже на 214, но в этой задаче шарик лежит между двумя точками. Нарисуйте фигуру. Определите свои переменные. Составьте уравнения и решите их.

233. Очень интересная задача. Различные его обратные значения использовались на протяжении веков для вычисления радиуса Земли. В этой задаче мы предполагаем, что знаем о Земле. Все, что вам нужно здесь, это теорема Пифагора. Одна сторона прямоугольного треугольника равна 90 003 r, 90 004 радиуса Земли, а гипотенуза равна 90 003 r 90 004 + 90 003 h 90 004, где 90 003 h 90 004 — высота маяка. Теорема Пифагора третья сторона треугольника.

234. Поставьте эту задачу аналогично 233, но известны другие переменные.

251–255. Вы можете сделать все это сразу, оставив вычисления напоследок. Пусть n — количество сторон правильного многоугольника. Проведите линии от центра фигуры к вершинам и к серединам сторон. У вас получится 2 n маленьких треугольников. Каждый из них представляет собой прямоугольный треугольник с гипотенузой R, катетом р, и другая нога а /2. Угол в центре равен 360°/(2 n ) = 180°/ n. Используя тригонометрию, вы можете легко написать уравнения, связывающие площадь правильного многоугольника по мере необходимости.

Ответы

26. (и). b = 40. So sin A  = cos B  = 9/41, cos A  = sin B  = 40/41, tan A 90 004  = 9/40, желто-коричневый B  = 40 /9.

(ii). b = 12. So sin A  = cos B  = 35/37, cos A  = sin B  = 12/37, tan A 9 0004  = 35/12, желто-коричневый B  = 12 /37.

(iii). c = 25. So sin A  = cos B  = 24/25, cos A  = sin B  = 7/25, tan A 90 004 = 24/7, коричневый  B  = 7 /24.

31. a  = 4 фута, b  = 4,8 фута, около 4 футов 10 дюймов.

34. A  = 27,55°, около 28°. c  = 2,6.

42. B  = 26,95° или 26°57′. c  = 11,3.

61. AB = 12/тангенс A + 12/тангенс B = 12(√3 + 1) дюймов, примерно 33 дюйма.

67. ( a √3)/2, ( a √3)/3 и ( a √3)/6 соответственно.

202. Расстояние = 50/тангенс 26°34′ = 100 футов. Высота = 50 + 100 tan 19°41′ = 85,8′ = 85’9″.

207. Расстояние = 175/тангенс 42°38′ = 190 футов. Рост = 175 — 190 тангенс 23°17′ = 93,23′ = 9’3″.

214. Два уравнения

0,293052 = тангенс 16°20′ = ч /(65 +  x ), и

0,3 = тангенс 21°19′ = ч/х .

где x — расстояние от ближайшей точки до основания дерева. Вы можете решить их одновременно за х и ч.

Расстояние x = 196 футов. Высота ч = 76,5 футов.

215. Если ч — высота воздушного шара, а х — расстояние по земле от точки А до точки непосредственно под воздушным шаром, то два эквариона равны

тангенс 27°19′ = ч/х и

тангенс 41°45′ = ч / (2 –  x )

Вы можете решить эту пару уравнений на х и ч.

Высота = 0,654 мили = 3455 футов.

233. Мелочь больше 18,5 миль.

234. 600 футов.

251–255. Площадь правильного n -угольника равна A = nra /2. Чтобы найти A через R, r, или a, , используйте соотношения

cos 180°/ n = r/R, и

тангенс 180°/ n = a /(2 r ).

Затем

(i) в пересчете на R, площадь A = nR ²  cos 180°/ n  sin 180°/ n ,

(ii) в пересчете на r, площадь A = nr ² tan 180&deg/ n , и

(iii) в пересчете на а, площадь A = na ² /(4tan 180&deg/ и ).

Проблема	Форма	(i) R	(ii) r	(iii) a 9079 9
251	треугольник	(3 R 2 √3)/4	3 р 2  √3	( a 2 √3)/4
252	квадратный	2 Р 2	4 р 2	a 2
253	пятиугольник	(5 R 2  sin 108°)/2	5 r 2 tan 36°	(5 a 2 tan 54°)/4
254	шестигранник	(3 R 2 √3)/2	2 р 2  √3	(3 a 2 √3)/2
255	восьмиугольник	2 Р 2  √2	8 r 2 tan 22°30′	2 a 2 tan 67°30′

Отступление от троек Пифагора

Это не имеет ничего общего с тригонометрией, но это интересно. Вы, наверное, заметили, как Кроули часто выбирал две стороны прямоугольного треугольника целыми числами, а третья тоже оказывалась целым числом. Как и в задаче 26, где все три прямоугольных треугольника имели целые числа в качестве сторон, а именно 9:40:41, 12:35:37 и 7:24:25. Кроме того, в начале этой страницы был треугольник 5:12:13 (на самом деле 10:24:26, но он похож на треугольник 5:12:13). И, без сомнения, вы уже знаете о прямоугольном треугольнике 3:4:5.

Итак, существуют ли другие специальные прямоугольные треугольники, все стороны которых являются целыми числами? Да и изучались они давно. Три числа a, b, и c такие, что a ²  +  b ²  =  c ² образуют пифагорейскую тройку , в честь Пифагора. Он жил около 550 г. до н. э. и, вероятно, знаю немало из них. Но древние вавилоняне около 1800 г. до н. э. знали их все, и многие были известны в других древних цивилизациях, таких как Китай и Индия.

Прежде чем читать абзац, посмотрите, сможете ли вы найти еще несколько пифагорейских троек. Не считайте за новые те, у которых есть общий множитель, например 6:8:10, так как они будут похожи на меньшие.

В « элементах » Евклида есть описание всех возможных пифагорейских троек. Вот современный парафраз Евклида. Возьмем любые два нечетных числа m и n, с m n и взаимно простые (то есть без общих множителей). Пусть a  =  mn, пусть b  = ( n ²  –  m ² )/2, и пусть 900 03 c  = ( n ²  +  м ^{2 9{2},}a2+b2=c2,}

 используется для нахождения длины любой стороны прямоугольного треугольника.

• В прямоугольном треугольнике один из углов имеет значение 90 градусов.
• Самая длинная сторона прямоугольного треугольника называется гипотенузой, и это сторона, лежащая против угла 90 градусов.
• Если длина гипотенузы помечена как

  ccc

  , а длины других сторон помечены как

  aaa

   и

  bbb

  , теорема Пифагора утверждает, что 9\circ90∘

  ). Прямоугольный треугольник – это треугольник, в котором один угол прямой. Соотношение между сторонами и углами прямоугольного треугольника является основой тригонометрии.

  Сторона, противолежащая прямому углу, называется гипотенузой (на рисунке сторона

  ссс

  ). Стороны, примыкающие к прямому углу, называются катетами (стороны

  aaa

  и

  bbb

  ). Сторона

  aaa

  может быть идентифицирована как сторона, прилегающая к углу

  BBB

  и напротив (или напротив) угла

  AAA

  . Сторона

  bbb

  — это сторона, примыкающая к углу

  AAA

  и противолежащая углу

  BBB

  .

  Прямоугольный треугольник: Теорему Пифагора можно использовать, чтобы найти значение длины недостающей стороны в прямоугольном треугольнике.

  Если длины всех трех сторон прямоугольного треугольника являются целыми числами, такой треугольник называется пифагорейским треугольником, а длины его сторон в совокупности называются пифагорейской тройкой.

  Теорема Пифагора

  Теорема Пифагора, также известная как теорема Пифагора, является фундаментальным соотношением в евклидовой геометрии. Он определяет отношение между тремя сторонами прямоугольного треугольника. В нем говорится, что квадрат гипотенузы (сторона, противоположная прямому углу) равен сумме квадратов двух других сторон. Теорему можно записать в виде уравнения, связывающего длины сторон

  aaa

  ,

  bbb

  9{2}}a2+b2=c2

  В этом уравнении

  ccc

  представляют длину гипотенузы, а

  aaa

  и

  bbb

  длины гипотенузы две другие стороны треугольника.

  Хотя часто говорят, что знание теоремы предшествовало ему, ^[2] теорема названа в честь древнегреческого математика Пифагора (ок. 570 – ок. 495 до н.э.). Ему приписывают первое зарегистрированное доказательство.

  Теорема Пифагора: 92a2+b2=c2

  .

  Поиск недостающей длины стороны

  Пример 1. Прямоугольный треугольник имеет длину стороны

  101010

  футов и длину гипотенузы

  202020

  футов.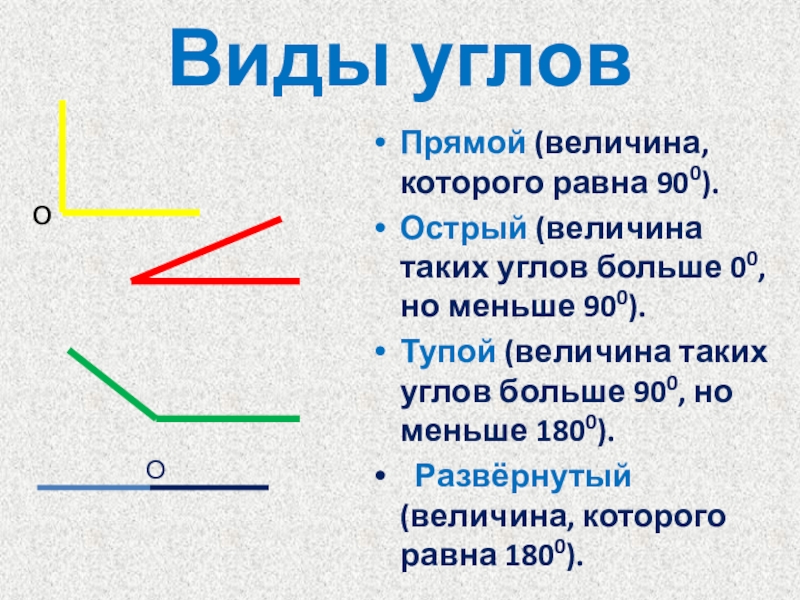 Найдите длину другой стороны. (округлить до десятых долей фута)

  Подставить

  a=10a=10a=10

   и

  c=20c=20c=20

   в теорему Пифагора и найти

  ббб

  .

  92} &=\sqrt{300} \\
  б &=17,3 ~\mathrm{футов}
  \end{выравнивание}
  }a2+b2(10)2+b2100+b2b2b2

  ​b​=c2=(20)2=400=300=300

  ​=17,3 фута​​

  Пример 2. Длина сторон прямоугольного треугольника

  333

  см и

  444

  см. Найдите длину гипотенузы.

  Подставить

  a=3a=3a=3

   и

  b=4b=4b=4

   в теорему Пифагора и найти

  ccc

  910 13 . 92} &=\sqrt{25} \\
  с &=5~\mathrm{см}
  \end{выравнивание}
  }a2+b232+429+1625c2c2

  ​c​=c2=c2=c2=c2=25=25

  ​=5 см​​

  Как работают тригонометрические функции

  Тригонометрические функции можно использовать для нахождения отсутствующих длин сторон в прямоугольных треугольниках.

  Цели обучения

  Узнайте, как тригонометрические функции используются для решения задач о прямоугольных треугольниках, и определите их входы и выходы

  Основные выводы

  Ключевые моменты 9{\ circ} 90 ∘

  ) Три тригонометрические функции, наиболее часто используемые для определения недостающей стороны прямоугольного треугольника: }sint=hypotenuseopposite​

  ,

  cos⁡t=adjacenthypotenuse\displaystyle{\cos{t} = \frac {adjacent}{hypotenuse}}cost=hypotenuseadjacent​

  , и

  tan⁡t=oppositeadjacent\displaystyle{\tan{ t} = \frac {противоположный} {смежный}} tant=соседнийпротивоположный​

Тригонометрические функции

Мы можем определить тригонометрические функции через угол

ttt

и длины сторон треугольника. Прилегающая сторона – это сторона, ближайшая к углу. (Смежный означает «рядом с».) Противоположная сторона – это сторона, расположенная напротив угла. Гипотенуза — это сторона треугольника, противоположная прямому углу, и она самая длинная.

Прямоугольный треугольник: Стороны прямоугольного треугольника относительно угла

ttt

.

При поиске отсутствующей стороны прямоугольного треугольника, когда единственной полученной информацией является измерение острого угла и длина стороны, используйте тригонометрические функции, перечисленные ниже: {t} = \frac {напротив} {гипотенуза}}sint=гипотенузанапротив​

Тригонометрические функции равны отношениям, которые связывают определенные длины сторон прямоугольного треугольника. При поиске отсутствующей стороны первым шагом является определение того, какие стороны и какой угол даны, а затем выбор подходящей функции для решения проблемы.

Оценка тригонометрической функции прямоугольного треугольника

Иногда вы знаете длину одной стороны треугольника и угла, и вам нужно найти другие измерения. Используйте одну из тригонометрических функций ( 9{\circ}34∘

и длину гипотенузы

252525

футов, найдите длину стороны, противоположной острому углу (округлите до десятых):

Прямоугольный треугольник: Дан прямоугольный треугольник с острого угла

343434

градусов и длины гипотенузы

252525

футов, найдите длину противоположной стороны.

Глядя на рисунок, найдите сторону, противоположную острому углу

343434 9{\circ}83∘

и длину гипотенузы

300300300

футов, найдите длину гипотенузы (округлив до десятых):

Прямоугольный треугольник: Дан прямоугольный треугольник с острым углом

838383

 градусов и длину гипотенузы

300300300

футов, найдите длину гипотенузы.

Глядя на рисунок, найдите гипотенузу к острому углу

838383

 градусов. Отношение сторон равно 9{\circ}\right)}} \\
x &= \frac{300}{\left(0,1218\dots\right)} \\
х &=2461,7~\mathrm{футы}
\end{выравнивание}
}costcos(83∘)x⋅cos(83∘)xxx​=hypotenuseadjacent​=x300​=300=cos(83∘)300​=(0,1218…)300​=2461,7 футов​​

Синус, косинус и Тангенс

Мнемосхему

SohCahToa можно использовать для определения длины стороны прямоугольного треугольника.

Цели обучения

Используйте аббревиатуру SohCahToa для определения синуса, косинуса и тангенса в терминах прямоугольных треугольников

Key Takeaways

Key Points

• Общая мнемоника для запоминания взаимосвязей между функциями синуса, косинуса и тангенса — SohCahToa.
• SohCahToa образован из первых букв « S ine is o pposite over h ypotenuse ( Soh ), C osine is 913 24 a djacent over h ypotenuse ( Cah ), Тангенс противоположен соседнему ( Тоа )».

Определения тригонометрических функций

Для прямоугольного треугольника с острым углом 

ttt

 первые три тригонометрические функции таковы:

• сайт}{гипотенуза} } sint=hypotenuseopposite​

• Косинус        

  cos⁡t=adjacenthypotenuse\displaystyle{ \cos{t} = \frac {adjacent}{hypotenuse} }cost=hypotenuseadjacent​

• Касательная      

  tan⁡t=oppositeadjacent\displaystyle{ \tan{t} = \frac {напротив}{adjacent} }tant=adjacentopposite​

Общая мнемоника для запоминания этих взаимосвязей — SohCahToa , образованная из первых букв « S ine is o pposite over h ypotenuse ( Soh ), 9 1324 C озин — это a djacent более ч ypotenuse ( Cah ), Тангенс противоположен соседнему ( 9{\ circ} 62∘

и смежная сторона

454545

футов, найдите длину противоположной стороны. (округлить до десятых)

Прямоугольный треугольник: Дан прямоугольный треугольник с острым углом

626262

градусов и смежной стороной

454545

футов, найти противоположную сторону длина.

Сначала определите, какую тригонометрическую функцию использовать, если дана смежная сторона, и вам нужно решить для противоположной стороны. Всегда определяйте, какая сторона дана, а какая неизвестна по острому углу ( 9\circ32∘

, гипотенуза равна 30 футам, а недостающая длина стороны равна противоположному катету,

xxx

футов.

Определите, какую тригонометрическую функцию использовать, если задана гипотенуза, и вам нужно решить для противоположной стороны. Вспоминая мнемонику « S ohCahToa», указанные стороны представляют собой гипотенузу и противолежащие стороны или «h» и «o», которые использовали бы «S» или синусоидальную тригонометрическую функцию.

sin⁡t=противоположная гипотенуза in⁡(32∘)=x3030⋅sin⁡(32∘)=xx=30⋅sin⁡(32∘)x=30⋅(0,529{\ круг} \ справа)} \\
x &= 30\cdot\left( 0.5299\dots\right) \\
х &= 15,9 ~\mathrm{футов}
\end{выравнивание}
}sintsin(32∘)30⋅sin(32∘)xxx​=hypotenuseopposite​=30x​=x=30⋅sin(32∘)=30⋅(0,5299…)=15,9 футов​​

Нахождение углов из отношений : Обратные тригонометрические функции

Обратные тригонометрические функции можно использовать для нахождения измерения острого угла прямоугольного треугольника.

Цели обучения

Использование обратных тригонометрических функций при решении задач на прямоугольные треугольники 9{-1}tan−1

.

Использование тригонометрических функций для определения отсутствующей стороны при заданном остром угле так же просто, как определение сторон относительно острого угла, выбор правильной функции, составление уравнения и решение. Найти недостающий острый угол по двум сторонам прямоугольного треугольника так же просто.

Обратные тригонометрические функции

Чтобы найти недостающий острый угол, используйте те же три тригонометрические функции, но используйте обратный ключ ( 9\circA∘

с противоположной стороной

12 футов12~\mathrm{feet}12 футов

, найдите острый угол с точностью до ближайшего градуса:

Прямоугольный треугольник: Найдите величину угла

9000 2 ААА

, если даны противолежащий катет и гипотенуза.

Из угла

AAA

даны стороны напротив и гипотенуза . Поэтому используйте тригонометрическую функцию синуса. ( Soh от SohCahToa)  Напишите уравнение и решите его, используя обратный ключ для синуса.
9{\ круг}
\end{выравнивание}
}sinA∘sinA∘A∘A∘A​=hypotenuseopposite​=2512​=sin-1(2512​)=sin-1(0.48)=29∘​​

Лицензии и атрибуты

Лицензионное содержимое CC, опубликованное ранее

• Курирование и доработка. Автор : Boundless.com. Лицензия : Общественное достояние: Неизвестно Авторские права

Лицензионный контент CC, конкретное указание авторства

• Прямоугольный треугольник. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
• Теорема Пифагора. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
• 346px-Rtriangle.svg.jpg. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
• 265px-Pythagorean. svg.jpg. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
• Тригонометрия прямоугольного треугольника. Предоставлено : OpenStax. Расположен по адресу : https://openstax.org/books/алгебра-и-тригонометрия/pages/7-2-right-triangle-trigonometry. Лицензия : CC BY-SA: Attribution-ShareAlike
• Тригонометрические функции. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
• 346px-Rtriangle.svg.jpg. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
• 265px-Pythagorean.svg.jpg. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
• Оригинальная фигура Джанет Хеймбах. Лицензия CC BY-SA 4.0. Предоставлено : Джанет Хеймбах. Лицензия : CC BY-SA: Attribution-ShareAlike
• Оригинальная фигура Джанет Хеймбах. Лицензия CC BY-SA 4.0. Предоставлено : Джанет Хеймбах. Лицензия : CC BY-SA: Attribution-ShareAlike
• CNX_Precalc_Figure_05_04_002.jpg. Предоставлено : OpenStax. Расположен по адресу : https://openstax.org/books/алгебра-и-тригонометрия/pages/7-2-right-triangle-trigonometry. Лицензия : CC BY-SA: Attribution-ShareAlike
• Тригонометрические функции. Предоставлено : Википедия. Расположен по адресу : https://en.wikipedia.org/wiki/Trigonometric_functions. Лицензия : CC BY-SA: Attribution-ShareAlike
• Тригонометрия прямоугольного треугольника. Предоставлено : OpenStax. Расположен по адресу : https://openstax.org/books/алгебра-и-тригонометрия/pages/7-2-right-triangle-trigonometry. Лицензия : CC BY-SA: Attribution-ShareAlike
• 346px-Rtriangle.svg.jpg. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
• 265px-Pythagorean.svg.jpg. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
• Оригинальная фигура Джанет Хаймбах. Лицензия CC BY-SA 4.0. Предоставлено : Джанет Хеймбах. Лицензия : CC BY-SA: Attribution-ShareAlike
• Оригинальная фигура Джанет Хеймбах. Лицензия CC BY-SA 4.0. Предоставлено : Джанет Хеймбах. Лицензия : CC BY-SA: Attribution-ShareAlike
• CNX_Precalc_Figure_05_04_002.jpg. Предоставлено : OpenStax. Расположен по адресу : https://openstax.org/books/алгебра-и-тригонометрия/pages/7-2-right-triangle-trigonometry. Лицензия : CC BY-SA: Attribution-ShareAlike
• Оригинальная фигура Джанет Хеймбах. Лицензия CC BY-SA 4.0. Предоставлено : Джанет Хеймбах. Лицензия : CC BY-SA: Attribution-ShareAlike
• CNX_Precalc_Figure_05_04_002.jpg. Предоставлено : OpenStax. Лицензия : CC BY-SA: Attribution-ShareAlike
• Оригинальная фигурка Джанет Хаймбах. Лицензия CC BY-SA 4.0. Предоставлено : Джанет Хеймбах. Лицензия : CC BY-SA: Attribution-ShareAlike
• Тригонометрия прямоугольного треугольника. Предоставлено : openstax. Расположен по адресу : https://openstax.org/books/алгебра-и-тригонометрия/pages/7-2-right-triangle-trigonometry. Лицензия : CC BY-SA: Attribution-ShareAlike
• Тригонометрические функции. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
• 346px-Rtriangle.svg.jpg. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
• 265px-Pythagorean.svg.jpg. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
• Оригинальная фигура Джанет Хеймбах. Лицензия CC BY-SA 4.0. Предоставлено : Джанет Хеймбах. Лицензия : CC BY-SA: Attribution-ShareAlike
• Оригинальная фигура Джанет Хеймбах. Лицензия CC BY-SA 4.0. Предоставлено : Джанет Хеймбах. Лицензия : CC BY-SA: Attribution-ShareAlike
• CNX_Precalc_Figure_05_04_002.jpg. Предоставлено : OpenStax. Расположен по адресу : https://openstax.org/books/алгебра-и-тригонометрия/pages/7-2-right-triangle-trigonometry. Лицензия : CC BY-SA: Attribution-ShareAlike
• Оригинальная фигурка Джанет Хаймбах. Лицензия CC BY-SA 4.0. Предоставлено : Джанет Хеймбах.