Калькулятор треугольника
Введите 3 значения, включая хотя бы одну сторону, в следующие 6 полей и нажмите кнопку «Рассчитать». Если в качестве единицы измерения угла выбран радиан, он может принимать такие значения, как пи/2, пи/4 и т. д.
Треугольник — это многоугольник с тремя вершинами. Вершина — это точка, в которой встречаются две или более кривых, линий или ребер; в случае треугольника три вершины соединены тремя отрезками, называемыми ребрами. Треугольник обычно называют его вершинами. Следовательно, треугольник с вершинами a, b и c обычно обозначается как Δabc. Кроме того, треугольники, как правило, описываются на основе длины их сторон, а также их внутренних углов. Например, треугольник, в котором все три стороны имеют одинаковую длину, называется равносторонним треугольником, а треугольник, в котором две стороны имеют одинаковую длину, называется равнобедренным. Когда ни одна из сторон треугольника не имеет одинаковой длины, он называется разносторонним, как показано ниже.
Засечки на ребрах треугольника — общепринятое обозначение, отражающее длину стороны, где одинаковое количество засечек означает одинаковую длину. Аналогичные обозначения существуют для внутренних углов треугольника, обозначаемых разным количеством концентрических дуг, расположенных в вершинах треугольника. Как видно из приведенных выше треугольников, длина и внутренние углы треугольника напрямую связаны, поэтому имеет смысл, что равносторонний треугольник имеет три равных внутренних угла и три стороны одинаковой длины. Обратите внимание, что треугольник, представленный в калькуляторе, показан не в масштабе; хотя он выглядит равносторонним (и имеет маркировку углов, которые обычно читаются как равные), он не обязательно является равносторонним и представляет собой просто изображение треугольника. При вводе фактических значений выходные данные калькулятора будут отражать форму входного треугольника.
Треугольники, классифицированные по их внутренним углам, делятся на две категории: прямоугольные и косоугольные. Прямоугольный треугольник — это треугольник, в котором один из углов равен 90°, и обозначается двумя отрезками, образующими квадрат в вершине, составляющей прямой угол. Самая длинная сторона прямоугольного треугольника, лежащая против прямого угла, называется гипотенузой. Любой треугольник, который не является прямоугольным, классифицируется как косоугольный и может быть либо тупоугольным, либо остроугольным. В тупоугольном треугольнике один из углов треугольника больше 90°, а в остроугольном треугольнике все углы меньше 90°, как показано ниже.
Прямоугольный треугольник — это треугольник, в котором один из углов равен 90°, и обозначается двумя отрезками, образующими квадрат в вершине, составляющей прямой угол. Самая длинная сторона прямоугольного треугольника, лежащая против прямого угла, называется гипотенузой. Любой треугольник, который не является прямоугольным, классифицируется как косоугольный и может быть либо тупоугольным, либо остроугольным. В тупоугольном треугольнике один из углов треугольника больше 90°, а в остроугольном треугольнике все углы меньше 90°, как показано ниже.
Факты, теоремы и законы треугольника
- Зная длины всех трех сторон любого треугольника, каждый угол можно вычислить с помощью следующего уравнения. Обратитесь к треугольнику выше, предполагая, что значения a, b и c известны.
Площадь треугольника
Существует несколько различных уравнений для расчета площади треугольника, в зависимости от того, какая информация известна. Вероятно, наиболее известное уравнение для вычисления площади треугольника включает его основание, b и высота h . «Основание» относится к любой стороне треугольника, где высота представлена длиной отрезка, проведенного от вершины, противоположной основанию, к точке на основании, образующей перпендикуляр.
Вероятно, наиболее известное уравнение для вычисления площади треугольника включает его основание, b и высота h . «Основание» относится к любой стороне треугольника, где высота представлена длиной отрезка, проведенного от вершины, противоположной основанию, к точке на основании, образующей перпендикуляр.
Зная длину двух сторон и угол между ними, можно использовать следующую формулу для определения площади треугольника. Обратите внимание, что используемые переменные относятся к треугольнику, показанному в калькуляторе выше. Учитывая а = 9, b = 7 и C = 30°:
Другой метод вычисления площади треугольника использует формулу Герона. В отличие от предыдущих уравнений, формула Герона не требует произвольного выбора стороны в качестве основания или вершины в качестве начала координат. Однако для этого требуется, чтобы длины трех сторон были известны. Опять же, в отношении треугольника, представленного в калькуляторе, если a = 3, b = 4 и c = 5:
Медиана, внутренний радиус и радиус описанной окружности
Медиана
Медиана треугольника определяется как длина отрезка, проходящего от вершины треугольника до середины противоположной стороны. Треугольник может иметь три медианы, каждая из которых будет пересекаться в центре тяжести (среднее арифметическое положение всех точек треугольника) треугольника. Обратитесь к приведенному ниже рисунку для пояснения.
Треугольник может иметь три медианы, каждая из которых будет пересекаться в центре тяжести (среднее арифметическое положение всех точек треугольника) треугольника. Обратитесь к приведенному ниже рисунку для пояснения.
Медианы треугольника представлены отрезками m a , m b и m c . Длину каждой медианы можно рассчитать следующим образом:
Где a, b и c представляют длину стороны треугольника, как показано на рисунке выше.
Например, учитывая, что a=2, b=3 и c=4, медиана m a может быть рассчитана следующим образом: круг, который поместится внутри заданного многоугольника, в данном случае треугольника. Внутренний радиус перпендикулярен каждой стороне многоугольника. В треугольнике внутренний радиус можно определить, построив две биссектрисы угла, чтобы определить центр треугольника. Внутренний радиус — это расстояние по перпендикуляру между центром вписанной стороны и одной из сторон треугольника.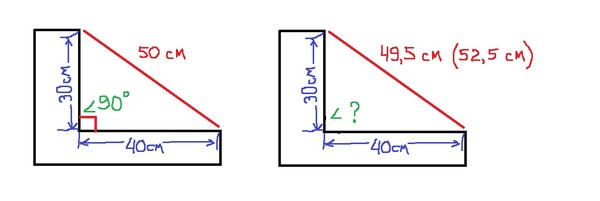 Можно использовать любую сторону треугольника, если определено перпендикулярное расстояние между стороной и центром вписанной стороны, поскольку центр вписанной стороны по определению равноудален от каждой стороны треугольника.
Можно использовать любую сторону треугольника, если определено перпендикулярное расстояние между стороной и центром вписанной стороны, поскольку центр вписанной стороны по определению равноудален от каждой стороны треугольника.
Для целей этого калькулятора внутренний радиус рассчитывается с использованием площади (Area) и полупериметра (s) треугольника по следующим формулам:
| внутренний радиус = |
| с = |
|
где a, b и c — стороны треугольника
Радиус окружности
Радиус окружности определяется как радиус окружности, проходящей через все вершины многоугольника, в данном случае треугольника. Центр этой окружности, где встречаются все серединные перпендикуляры каждой стороны треугольника, является центром описанной окружности треугольника и является точкой, от которой измеряется радиус описанной окружности. Центр описанной окружности треугольника не обязательно должен находиться внутри треугольника. Стоит отметить, что у всех треугольников есть описанная окружность (окружность, проходящая через каждую вершину) и, следовательно, радиус описанной окружности.
Центр описанной окружности треугольника не обязательно должен находиться внутри треугольника. Стоит отметить, что у всех треугольников есть описанная окружность (окружность, проходящая через каждую вершину) и, следовательно, радиус описанной окружности.
Для целей данного калькулятора радиус описанной окружности рассчитывается по следующей формуле:
| радиус описанной окружности = |
|
Где а — сторона треугольника, а А — угол, противоположный стороне а
Хотя сторона а и угол А используются, в формуле можно использовать любую из сторон и соответствующие им противоположные углы.
ПРЯМОУГОЛЬНАЯ ТРИГОНОМЕТРИЯ — Mathtec
названия сторон и вершин треугольника
небольшая подборка
ТРИГОНОМЕТРИЯ ПРЯМОГО УГЛА
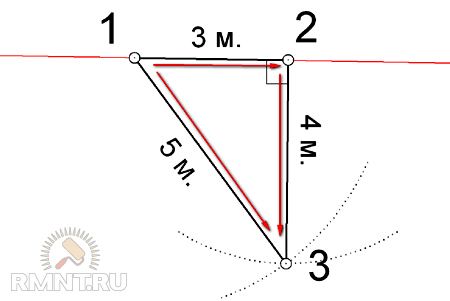
Теорема Пифагора, также известная как теорема Пифагора, используется для вычисления длин сторон прямоугольных треугольников. В прямоугольном треугольнике один угол равен 90 градусов, см. рис. 1. или рис. 2, отмечен маленьким квадратом в левом нижнем углу. Если мы знаем длину любой из двух сторон треугольника, мы можем вычислить третью неизвестную сторону треугольника.
В прямоугольном треугольнике один угол равен 90 градусов, см. рис. 1. или рис. 2, отмечен маленьким квадратом в левом нижнем углу. Если мы знаем длину любой из двух сторон треугольника, мы можем вычислить третью неизвестную сторону треугольника.
Рис.2. Прямоугольный треугольник
Пифагор был известным греческим математиком и философом. Хотя теорема названа в его честь, он, вероятно, не изобрел ее, поскольку есть свидетельства того, что многие культуры использовали эту теорему за сотни лет до Пифагора. Но есть разница между использованием метода и его доказательством, поэтому ему приписывают его доказательство. Более длинная сторона треугольника называется гипотенузой, это греческое слово, как и Пифагор.
ТАК ЧТО ЗНАЧИТ ФОРМУЛА?
Формула гласит, что «Квадрат гипотенузы (более длинной стороны)» равен сумме квадратов двух более коротких сторон (a и b).
Рис.3. Классический треугольник 3,4,5
Прямоугольный треугольник (далее называемый треугольником) имеет длину основания 4 см и высоту по вертикали 3 см, рассчитайте длину гипотенузы. Нарисуйте схему.
Нарисуйте схему.
Составьте уравнение. Подставьте числа в формулу. Возведите числа в квадрат и сложите результаты вместе. Не забудьте в конце извлечь квадратный корень из с. Этот конкретный треугольник называется треугольником 3,4,5 по понятным причинам и используется во многих практических приложениях. Математика, используемая здесь, довольно проста, и мы скоро рассмотрим, как это сделать с помощью калькулятора, и покажем вам ярлык, который вы можете использовать, если хотите.
Это может показаться немного придирчивым, но квадратный корень из 25 имеет 2 решения: одно положительное, как в приведенном выше, и одно отрицательное, как в -5см. Это потому, что -5 x -5 также равно 25. Технически ответ равен +/- 5 см, и тогда вы бы заявили, что +5 — правильный ответ. Это то, что нужно иметь в виду на последующие годы.
Визуально это можно показать ниже на рис.4.
Рис.4. Графический подход к теореме Пифагора.
Как использовать калькулятор для приведенного выше уравнения
Этот метод на калькуляторе является кратким методом для определения длины длинной стороны треугольника. Вставьте символ квадратного корня, квадраты длин сторон заключите в скобки. Это позволяет быстро получить решение. Не просто запишите ответ, покажите, как вы работаете, и не забудьте единицы измерения (см, м, км, кг и т. д.) и умейте округлять до двух знаков после запятой.
Вставьте символ квадратного корня, квадраты длин сторон заключите в скобки. Это позволяет быстро получить решение. Не просто запишите ответ, покажите, как вы работаете, и не забудьте единицы измерения (см, м, км, кг и т. д.) и умейте округлять до двух знаков после запятой.
ПРИМЕР РАСЧЕТА
Упражнение 1. Вычислите длину гипотенузы в этих треугольниках. Дайте ответ с точностью до 2 знаков после запятой.
ОТВЕТЫ:
1) 10,30 см
2) 3,22 м
3) 15,26 м
4) 102,00 см
НАЙТИ КОРОТКУЮ СТОРОНУ ПРЯМОГО УГЛА D ТРЕУГОЛЬНИК
Чтобы найти короткую сторону прямоугольного треугольника, мы переформулируем формулу Пифагора так, чтобы a или b были предметом. Затем выполните ту же процедуру, что и выше, для нахождения длины гипотенузы. Вы также можете использовать быстрый метод на калькуляторе.
Упражнение 2. Вычислите длины неизвестных меньших сторон, используя теорему Пифагора.
Ответы на 2dp
1)95,70 м
2)182,93
3)13,86 м
4)63,11 м
Упражнение 3(а) Зная высоту крыши и размеры основания, рассчитайте общую длину крыши Парфенона.
3(b) Рассчитайте приблизительную высоту балки крыши, учитывая, что фермы образуют равносторонний треугольник.
На стройплощадке строится сарай. Строитель решает скрепить одну из стеновых рам куском дерева размером 4 x 2 дюйма. Это удержит конструкцию на месте, пока оставшаяся древесина будет прибита на место. По данным замерам рассчитайте минимальную длину диагональных раскосов, крепящих раму. Ответ в этом случае будет приблизительным, как это обычно бывает со многими практическими примерами.
ответ 244,13 см |
Древесина, используемая в этих строительных работах, была получена с Mitre 10 Mega Lincoln Rd в отрезках по 5 м, поэтому часто необходимо выполнять расчеты и распиливать древесину на земле на строительной площадке.