Как вычислить угол 90 градусов: Как найти прямой угол

Camino Угол 90 градусов, ∅80/125 Condensing (71.MT7.00.49) в Санкт-Петербурге

• Описание
• Отзывы
• Доставка

Данные оборудования

• 
  Родина бренда

  (Россия)

• 
  Сборка

  (Россия)

• 
  Производитель

  Camino

• 
  Артикул производителя

  71.MT7.00.49

• 
  Гарантия

  12 мес.

Потребительские характеристики

• 
  Материал дымохода
  
• 
  Цвет
  
• 
  Диаметр внутр.

  мм

• 
  Диаметр наруж.

  мм

• 
  Диаметр общ.

  мм

• 
  Утеплитель

  нет

Размеры, вес, подключение

• 
  Размер (В×Ш×Г)
  
• 
  Вес

  0. 00 кг

Самовывоз

Вы можете самостоятельно забрать свой заказ в Санкт-Петербурге из филиала транспортной компании, которую выбрали при оформлении заказа. Это самый распространенный и недорогой способ доставки. Однако, транспортная компания может осуществить и адресную доставку.

Внимание!!! Обязательно согласуйте стоимость адресной доставки во избежание недоразумений.

Инструкция о порядке получения заказа будет отправлена на Ваш адрес электронной почты.

Ориентировочный расчет доставки в Санкт-Петербург и Ленинградскую область компанией Деловые Линии

заводская упаковка+ жесткая упаковка+ картонная коробка+ дополнительная упаковка+ воздушно-пузырьковая плёнка+ мешок+ паллетный борт (только до терминала)

Ориентировочный расчет доставки ТК СДЭК

Ответы на частые вопросы

Как купить, если я не в Москве?

Если Вам необходима доставка оборудования в регионы РФ, то доставка оборудования будет осуществляться транспортной компанией, которую мы можем подобрать сами из наиболее оптимальных вариантов или если Вы работали с другой компанией — предложить свою.
При заказе в регионы РФ заказ оплачивается предварительно: безналичным расчетом в банке или банковской картой онлайн.

В какие города вы осуществляете доставку?

Мы осуществляем доставку в регионы РФ транспортными компаниями ПЭК, Деловые Линии, Байкал-Сервис, Энергия, ЖелДорЭкспедиция и др. Список городов доставки представлен в разделе города доставки.

Как можно оплатить заказ?

Варианты оплаты зависят о того каким способом будет
осуществляться доставка оборудования.

• При самовывозе вы можете воспользоваться любым удобным для вас способом:
  наличными, банковской картой в офисе, банковской картой онлайн, получить счет для оплаты в банке.
• При доставке экспедитором: наличными в момент получения. Безналичным
  расчетом, банковской картой онлайн — при предварительной оплате заказа.
• При доставке через транспортные компании или в регионы РФ: безналичным расчетом, банковской картой онлайн.

Как будет осуществляться доставка по России

1. Доставка оборудования в регионы России осуществляется
   после подтверждения заказа и его оплаты. При оплате банковской картой
   онлайн Вам будет предоставлена информация о порядке оплаты заказа на
   сайте Сбербанка. Если оплата осуществлялась безналичным расчетом, то
   основанием для оплаты является счет, который будет отправлен на Ваш
   адрес эл. почты. При оплате счета через банк взимается комиссия. Мин.
   комиссия, как правило, в отделениях Сбербанка.

2. После поступления денежных средств на счет компании, в
   течение двух дней осуществляется отправка товара транспортной компанией.

3. После отправки на Ваш адрес будет выслана вся информация
   о грузе посредством SMS-сообщения или на адрес эл. почты, указанный при
   оформлении заказа.

4. По прибытии груза в назначенный пункт, менеджеры
   транспортной компании известят Вас о необходимости его получения.

Какой у вас телефон?

+7(495)48-132-48

Хочу отправить заказ от Юр. лица

Мы принимаем заявки в Excel на адрес [email protected]

Хочу сделать большой или получить КП, я — Физ. лицо

Если Ваша заявка в Excel и с артикулами. Мы принимаем заявки на адрес [email protected]

Хочу сделать заказ, я — Физ. лицо

Вы можете оформить заказ на сайте, наш менеджер свяжется с Вами по указанным контактам

У меня проблемы

Бывает. Присылайте свои запросы на адрес [email protected] или по телефону +7(495)48-132-48

Я — поставщик

Вы можете прислать свое предложение на [email protected]

Я сделал заказ, как узнать статус

Заказов очень много. Приносим свои извинения. Можно позвонить +7(495)48-132-48

Работаете ли вы с НДС?

Работаем, мы официальный магазин. Предоставляем все документы: счет, УПД, договор.

Почему я должен вам доверять?

Нет ни одной компании в РФ с одноименным названием. Теплодвор — это запатентованное имя, которым обладаем только мы. Это не дешевая услуга, которая подразумевает раскрытие всех персональных данных ее владельцев. Выбирая Теплодвор вы получаете гарантию от Государственных органов и можете быть уверены в качестве предоставляемых услуг. Для обсуждения подробностей — +7(495)48-132-48

Приобретая camino Угол 90 градусов, ∅80/125 Condensing с доставкой в Санкт-Петербург по выгодной цене, Вы получаете не только товар высокого качества, но и гарантию того, что данная продукция сертифицирована и имеет всю необходимую документацию.

Если нет времени для самостоятельного изучения, Вы можете обратиться за получением консультации к любому из наших менеджеров по телефону, Whatsapp или электронной почте, указанных на странице Контакты.

Мы работаем как с физическими лицами так и с юридическими лицами и предпринимателями с НДС.
Вы можете купить Camino Угол 90 градусов, ∅80/125 Condensing в нашем интернет-магазине с доставкой или забрать заказ самостоятельно.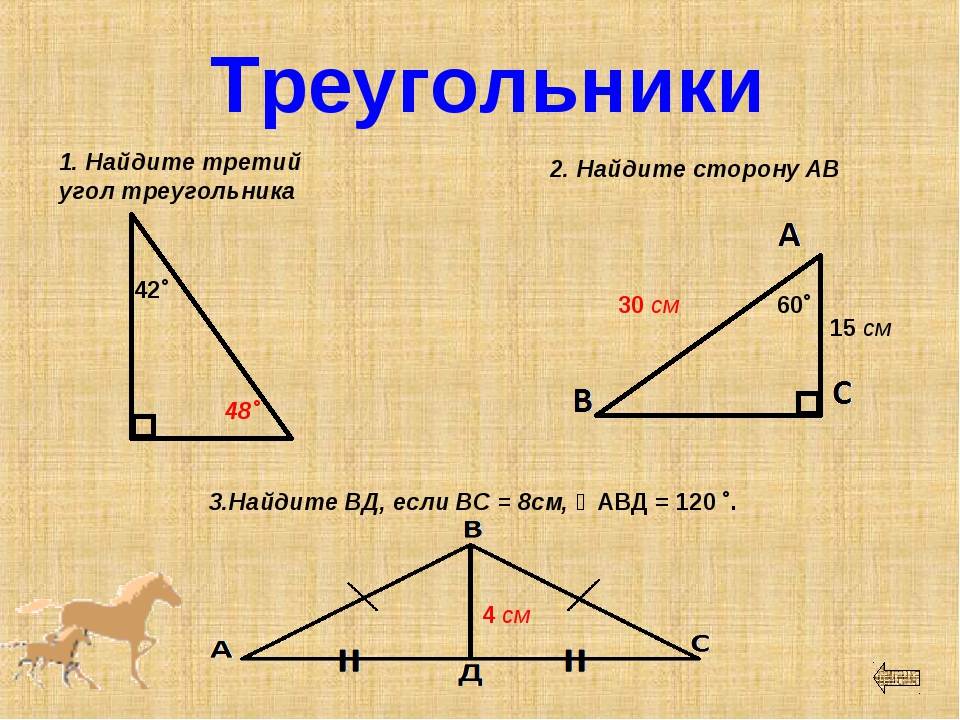

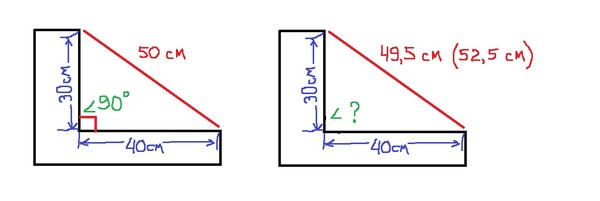
Углы 30, 45, 60, 90 градусов: наглядные, боевые, электрические

Можно определить углы 30, 45, 60, 90 градусов с помощью своей ладони.

Содержание

1. Градусы наглядные: как их определить с помощью своей ладони
2. Градусы стихотворные и число «пи»
3. Градусы боевые: почему наши деды победили
4. Градусы электрические: отклонение между напряжением и током
5. Градусы драматические: косинус 90 градусов равен нулю
6. Градусы из радиоточки
7. Градусы музыкальные

Градусы наглядные: как их определить с помощью своей ладони

Рис. 1. Углы 0, 30, 45, 60 и 90 градусов.

Наша рука, оказывается, очень даже может помочь с величинами углов, с градусами. Если посмотреть на нее под определенным углом зрения (см. рис. 1), то вот они, родимые: 0 градусов, 30, 45, 60 и даже 90 градусов!

Почему нам так важны именно эти величины? Почему нас могут интересовать углы 0, 30, 60 и 90 градусов, а также 45? Нет бы поинтересоваться, скажем, углами 15, 20, 75 или 80 градусов…

Оказывается, все дело в синусах и косинусах! Ибо синус нуля градусов есть ноль, а косинус 90 градусов — тоже равен нулю. Синус 30 градусов равен половинке единицы. Такое же значение 0,5 дает косинус 60 градусов.

А вот 45 градусов интересны тем, что синус и косинус 45 градусов равны между собой. Это значит, что тангенс 45 градусов будет равен единице. Ведь мы помним, что тангенс угла есть частное от деления синуса угла на косинус угла.

Но не только об этом хотелось сказать, глядя на рисунок…

Градусы стихотворные и число «пи»

Есть такое число – «пи». Оно почему-то равно 3,14. Хотя не совсем так. Это число с бесконечным количеством цифр после запятой. После запятой стоят не только цифры 1 и 4, но и множество других цифр.

Первый десяток цифр числа «пи» легко написать, если запомнить необычное стихотворение. Правда, стихи про «пи» нужно писать со старинной буквой «ять» — ведь и число «пи» очень старое, и стихотворение совсем не молодое:

Кто и шутя, и скоро пожелаетъ
Пи узнать число  — ужъ знаетъ

Зачем в стихотворении стоит «ять» на конце? И при чем тут «пи»? Все очень просто: считаем буквы в словах стихотворения и подставляем цифры в число «пи».

Получается, кто=3, и=1, шутя=4, и=1, скоро=5 и так далее: 3,1415926536… Многоточие на конце — это значит, что есть продолжение цифрам, бесконечное продолжение.

Причем тут градусы? При том, что «пи» — это величина развернутого угла, но не в градусах, а в радианах (другая единица измерения величины угла). «Пи» радиан есть угол величиной 180 градусов.

Как говорят математики, отсюда нетрудно догадаться, что 0 градусов есть ноль радиан. 90 градусов есть «пи пополам» радиан. Нам этот термин «пи пополам» еще пригодится далее. Все остальные градусы таким же образом можно свести к разным частям числа «пи».

Получается, что мы теперь знаем стишок про 180 градусов — стишок про «пи»! Что это дает?

Градусы боевые: почему наши деды победили

Плывет боевой корабль. Вернее, идет боевой корабль, ибо корабли не плавают, а ходят. Штурман прокладывает курс на карте. И вдруг появляется супостат. Тревога!

Штурман откладывает карту в сторону. Достает маневренный планшет. Теперь он отслеживает на нем положение корабля относительно одного противника или сразу нескольких противников.

Тут — сплошные градусы. Кто из супостатов виден под каким углом? Угол есть решающая величина. Приходится учитывать как углы, так и их синусы, и косинусы.

Кто в школе учился, тот помнит, что синус и косинус угла не может быть больше единицы. Хоть что делай, больше единицы не получается.

А вот в годы войны у штурмана боевого корабля косинусы углов доходили порой до четырех! Потому и победили, что делали невозможное! Даже с косинусами, ограниченными правильной математикой!

Так что запомним вопреки математике: в годы войны косинусы углов могут доходить до «четырех». В том числе, поэтому наши деды победили!

Градусы электрические: отклонение между напряжением и током

Ну, синус? Ну, косинус? И что тут такого? Спросим любого человека, например, возле пивного ларька, что такое синус и как давно он пользовался косинусом после школы. Что услышим в ответ?! Во, именно «это» и услышим.

Вместе с тем мы постоянно живем, можно сказать, под градусом, точнее, под косинусом! Ежедневно мы пользуемся электричеством: нажимаем кнопки и выключатели, и дело с концом — все светится, крутится, работает.

Чтобы электричество выполняло свое предназначение, нужно электрическое напряжение и электрический ток. Обе «субстанции» должны быть вместе и одновременно. Но эти две величины могут иметь между собой угол отклонения, измеряемый «косинусом фи», как выражаются энергетики на своем профессиональном языке.

Если отклонение напряжения от тока есть ноль градусов, то электрическая мощность будет получена умножением величины напряжения на величину тока.

Допустим, подключаем электрообогреватель. Он начинает излучать тепло, равное по мощности этой самой величине: напряжение 220В (двести двадцать вольт) умножить на ток, скажем, 5А (пять ампер) равно 1КВт (1 киловатт) мощности. Становится тепло!

Если между напряжением и током есть отклонение, хотя бы на 1 градус, то придется перемножать не только напряжение и ток, но и полученный результат дополнительно умножать на косинус угла отклонения. Ноль градусов отклонения — косинус равен единице, умножение на единицу ничего не меняет. А вот косинус всего лишь 1-го градуса возможного отклонения уже меньше единицы. Не намного, но меньше. Это значит, что греть наша батарея будет уже слабее.

Чем больше отклонение электрического напряжения от электрического тока, чем будет больше между ними градусов так называемого угла «фи». Тем слабее будут греть батареи, хуже станет накал лампочек, и вообще будет меньше электричества.

И не говорите теперь, что косинус — это абстракция, которую мы оставили в школе навсегда…

Градусы драматические: косинус 90 градусов равен нулю

А что как напряжение и ток отклоняются друг от друга на 90 градусов?! Ведь косинус такого угла равен нулю. Умножение на ноль есть ноль. Это, что называется, страшный сон энергетиков — ужасная апокалиптическая драма!

Представьте себе, газ сжигается на тепловых электростанциях, вода крутит турбины на гидроэлектростанциях, нейтроны делятся в реакторах атомных электростанций. Ток «бежит» по проводам в дома. А там — косинус угла «фи» равен нулю — полный швах! Батареи не греют, лампочки не светятся, холодильники не работают.

Чтобы мысленный эксперимент с отклонением напряжения и тока на 90 градусов не стал реальностью, энергетики по всему миру постоянно следят за «косинусом фи». Денно и нощно, без устали, без перерывов.

Почему отклоняются напряжение и ток? Из-за потребителей электричества! Нет, не из-за домашних электрических обогревателей. И не из-за домашних лампочек накаливания. Но из-за оборудования заводов и фабрик.

Везде, где крутятся электромоторы, их «кручение» приводит как бы к обратному закручиванию электричества. Работающее оборудование возвращает энергетикам в электрические сети сдвинутое между собой напряжение и ток.

Образно говоря, чтобы крутить моторы, электричество должно «упираться» во что-то. И из-за этого понемногу «проворачивается» в обратную сторону. Что и приводит к возникновению угла сдвига между напряжением и током.

Если не следить за последствиями такого «сдвига», то угол между напряжением и током будет постоянно расти. Косинус фи начнет уменьшаться. Электростанции начнут работать сначала чуть-чуть вхолостую, потом все больше и больше, потом еще больше…

Градусы из радиоточки

Если напряжение и ток встанут друг относительно друга на 90 градусов — это будет недопустимое отклонение или «сдвиг по фазе на пи пополам»! Тогда электричество останется в проводах, но оно ничего не будет греть, освещать, двигать.

«Сдвиг по фазе на пи пополам» есть расхожее выражение, которое означает абсолютную неприемлемость того или иного действия, поступка.

Пришло оно к нам из того самого электротехнического «косинуса фи».

Про сдвиг между напряжением и током можно написать не одну драму с яркими событиями и участниками. Но мы не будем это делать, ибо наши энергетики не допустят подобного хода событий…

Кстати, кто помнит еще советское радио, что звучало практически в каждом доме? Там по утрам во многих городах сообщали не только про погоду. Погода — это тоже градусы, но другие.

Из радиоточки строго так говорили, обычно после прогноза погоды: «на сегодня режим энергопотребления установлен два тире два» или «.., два тире один». Это про «наши» градусы, про «косинус фи»!

Что это за режимы такие: 2-2, 2-1 и другое? То были прямые указания предприятиям, как они должны именно сегодня компенсировать возникающие сдвиги между напряжением и током.

Энергетики шли к компенсирующим установкам и включали озвученные по радио режимы. Вот ведь насколько важны углы! Про них даже по центральному радио (с местным уклоном, разумеется) вещали ежедневно.

А вы говорите градусы, синусы, косинусы! И зачем мы их в школе «проходили», если вокруг нас их как не было, так и нет? Оказывается, были, есть и будут. Даже в обычной электрической розетке, в лампочке, в утюге.

Градусы музыкальные

Для тех, кто «добрался» до конца — маленький сюрприз: музыкальные «градусы». Вот как, оказывается, можно сыграть на фортепиано про число «пи» с точностью аж до 122 знаков после запятой. Музыка «развернутого угла 180 градусов»!

Словами добавить нечего, достаточно послушать. И все это про «пи» и про градусы, которые в школе «прошли» и забыли:

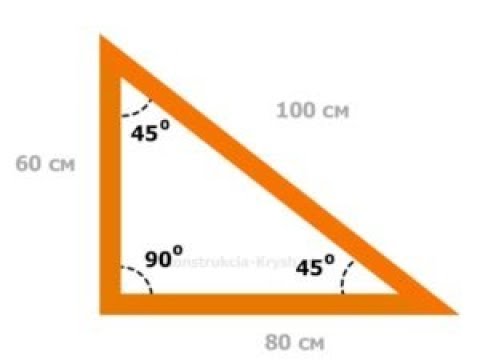
30-60-90 Треугольник. Теорема, соотношение и формула 04 Пол Маццола

Что такое 30-60-90 треугольник?

Треугольник 30-60-90  – это прямоугольный треугольник, в котором три внутренних угла равны 30° , 60° и 90° . Прямоугольные треугольники с внутренними углами 30-60-90 известны как особых прямоугольных треугольников 9.0018 .

Особые треугольники в геометрии из-за сильных взаимосвязей, которые раскрываются при изучении их углов и сторон.

Что такое треугольник 30-60-90

Во всех треугольниках легко понять отношения между углами и их противоположными сторонами. Чем больше угол, тем длиннее противоположная сторона.

Соотношение треугольников между углами и противоположными сторонами

Это означает, что из трех внутренних углов наибольший внутренний угол лежит напротив самой длинной из трех сторон, а наименьший угол будет находиться напротив самой короткой стороны.

В прямоугольном треугольнике напомним, что сторона, противолежащая прямому углу (наибольшему углу), называется гипотенузой (самая длинная сторона, а две другие стороны называются катетами.

30-60-90 отношение треугольника

A Треугольник 30-60-90 градусов является особым прямоугольным треугольником, поэтому длины его сторон всегда соответствуют друг другу Соотношение сторон соответствует соотношению треугольника 30-60-90:

• угол) = x

• Гипотенуза (против угла 90 градусов) = 2 x

• Длинная сторона (против угла 60 градусов) = x √3

30- Соотношение треугольников 60-90 и теорема

Теорема треугольника 30-60-90

Эти три специальных свойства можно рассматривать как теорему треугольника 30-60-90, и они являются уникальными для этих специальных прямоугольных треугольников:

1. Гипотенуза самая длинная сторона) всегда в два раза длиннее короткой ноги

2. Длина более длинного катета равна длине короткого катета, умноженной на √3

3. Если известна длина любой стороны треугольника 30-60-90, можно найти недостающие длины сторон

Другими интересными свойствами треугольников 30-60-90 являются:

Другие интересные свойства специальных прямоугольных треугольников

Как решить треугольник 30-60-90

Образование — это знание того, что треугольники 30-60-90 имеют три заложенных свойства в теореме. Мудрость заключается в том, чтобы знать, что делать с этим знанием. Предположим, у вас есть 30-60-90 треугольник:

Как решить треугольник 30-60-90

Мы знаем, что гипотенуза этого треугольника в два раза больше длины короткого катета:

Мы также знаем, что длинный катет — это произведение короткого катета на квадратный корень из 3:

Мы установили специальное число 30-60-90, чтобы продемонстрировать простоту нахождения длины трех сторон. Попробуйте решить эту задачу:

30-60-90 Пример задачи треугольника

Длинная сторона равна короткой стороне, умноженной на √3 , поэтому можете ли вы вычислить длину короткой стороны? Вы сказали 5?

Длина гипотенузы всегда в два раза больше длины короткого катета. Вы получили 10 ?

Вы можете создать свою собственную формулу треугольника 30-60-90, используя известную информацию в вашей задаче и следующие правила. Эта таблица правил треугольника 30-60-90 поможет вам найти недостающие длины сторон.

30-60-90 правила треугольника

правила треугольника 30-60-90

Если вы знаете. ..	Тогда…	Чтобы получить…
Гипотенуза	Разделить на 2	Короткая ножка
Короткая ножка	Умножить на 2	Гипотенуза
Короткая ножка	Умножить на √3	Длинная ножка
Длинная ножка	Разделить на √3	Короткая ножка

При работе с треугольниками 30-60-90 у вас может возникнуть соблазн установить соотношение между гипотенузой и длинным катетом. Это соотношение сложно из-за квадратного корня из 3,9.0003

Работайте осторожно, концентрируясь на соотношении гипотенузы и короткого катета, а затем короткого катета и длинного катета.

Вы заметите, что наши примеры до сих пор предоставляли только информацию, которую можно было бы легко «подключить», используя наши три свойства. Иногда геометрия не так проста.

30-60-90 правила треугольника

Что, если длинная сторона помечена простым целым числом?

Вы вскакиваете в проблему, поскольку для получения короткого катета нужно просто разделить длинный катет на квадратный корень из 3, а затем удвоить полученное значение, чтобы получить гипотенузу.

Но вы не можете оставить задачу так:

Правила математики не допускают радикала в знаменателе, поэтому вы должны рационализировать дробь. Умножьте числитель и знаменатель на √3 :

Это упрощает до:

Если вы не указали десятичный ответ, это может быть вашим окончательным ответом для длины короткой стороны. Удвоение дает 18 √3 для гипотенузы.

Еще один предупреждающий флаг с 30-60-90 треугольников заключается в том, что вы можете настолько увлечься тремя свойствами, что потеряете из виду сам треугольник. Это по-прежнему треугольник, поэтому сумма его внутренних углов должна составлять 180° , а три его стороны должны соответствовать теореме Пифагора:

Вы можете использовать теорему Пифагора, чтобы проверить свою работу или ускорить решение.

Треугольник 30-60-90 и теорема Пифагора

Примеры треугольника 30-60-90

У прямоугольного треугольника короткая сторона имеет длину 14 метра  с измерением противоположного угла 30° . Каковы две другие длины?

Треугольник 30-60-90 — нахождение недостающих длин

Мы сразу знаем, что треугольник равен 30-60-90, так как сумма двух идентифицированных углов составляет 120° :

Недостающий угол измеряется 60° . Отсюда следует, что гипотенуза равна 28 м , а длинный катет равен 14 м  * √3 .

Что у вас есть треугольник с гипотенузой, обозначенной 2,020  мм , короткая сторона обозначена 1,010  мм , а длинная часть — 1,010√3 .

Ваше знание треугольника 30-60-90 поможет вам сразу это распознать. Вы можете уверенно обозначить три внутренних угла, потому что видите взаимосвязь между гипотенузой и коротким катетом, а также между коротким катетом и длинным катетом.

Вот более сложная задача. Какова длина более короткой стороны, отрезок прямой MH ?:

Пример специальной задачи с треугольником

Вы сказали 50 дюйма ? На самом деле это два треугольника 30-60-90, что означает гипотенузу MA  также 100 дюймов , что означает кратчайший катет MH 900 45  есть  50  дюйма .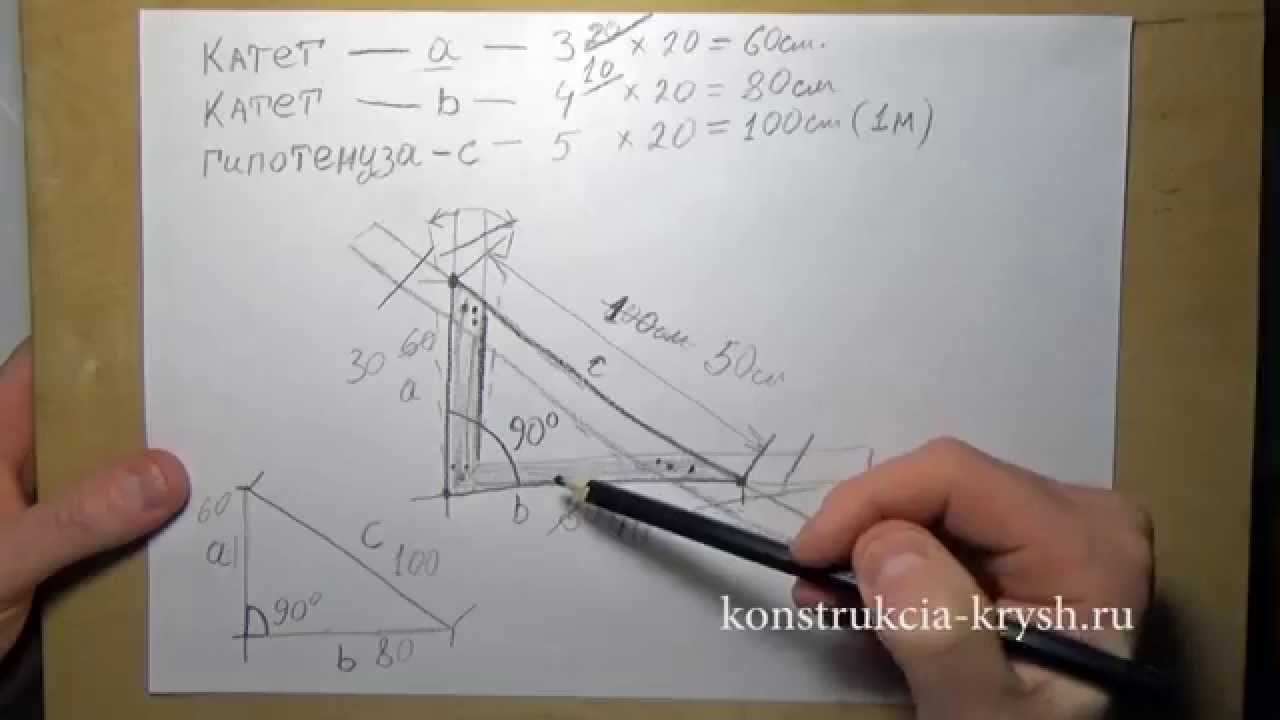

Как найти угол в прямоугольном треугольнике?

Треугольники представляют собой трехсторонние замкнутые многоугольники, образованные пересечением трех линий. В повседневной жизни встречается очень часто. Это одна из основных фигур геометрии. У него три стороны, три угла и три вершины. Прямоугольный треугольник – это треугольник, у которого один из углов всегда равен 90°. Для прямоугольных треугольников выведена теорема Пифагора, которая гласит, что квадрат гипотенузы (наибольшая сторона) равен сумме квадратов основания и перпендикуляра.

Зная длину по крайней мере двух сторон прямоугольного треугольника, мы можем найти значение любого угла прямоугольного треугольника. Для этого мы используем различные тригонометрические функции, такие как синус, косинус, тангенс, котангенс, сек и косек. Они помогают нам связать углы прямоугольного треугольника с его сторонами.

Свойства

• Среди трех вершин есть прямоугольная
• Сторона, противоположная прямоугольной вершине, называется гипотенуза .
• Длина сторон соответствует теореме Пифагора, которая гласит:

гипотенуза ² = основание ² + высота ²

90 311

• Гипотенуза — самая длинная сторона прямоугольного треугольника. .
• Углы, отличные от прямого угла, являются острыми, так как значение меньше 90 ^o

Тригонометрические функции

ABC — прямоугольный треугольник, в котором ∠B — прямой угол

• cosθ: Это дает отношение основания к гипотенузе прямоугольного треугольника.

cosθ = основание / гипотенуза

• sinθ: Это дает отношение высоты к гипотенузе прямоугольного треугольника.

sinθ = высота / гипотенуза

• tanθ: Это отношение высоты к основанию прямоугольного треугольника.

tanθ = высота / основание cosθ

cosecθ: Обратно sinθ

Чтобы найти углы прямоугольного треугольника, мы можем взять обратное тригонометрическое отношение данных сторон треугольника.

Пример:

Если sinθ = x, то мы можем написать

θ = sin ^-1 х.

Возвращает угол, для которого значение синуса угла равно x.

Аналогично, существуют cos ^-1 θ, tan ^-1 θ, cot ^-1 θ, sec ^-1 θ и cosec ^-1 θ

Примеры задач

Вопрос 1. Дан прямоугольный треугольник, основание которого равно 10 см, а гипотенуза равна 20 см. Найдите значение угла при основании.

Решение:

Дано, Основание = 10 см

Гипотенуза = 20 см

Пусть значение угла при основании равно θ. Мы можем написать

cosθ = основание / гипотенуза = 10/20 = 1/2

θ = cos ^-1 (1/2) = 60 ^o

Таким образом, значение угла при основании равно 60 ^о .

Вопрос 2. Найдите величину углов прямоугольного треугольника, если один из острых углов в 2 раза больше другого.

Решение:

Поскольку мы знаем, что сумма всех трех углов треугольника равна 180 ^o .

Поскольку один из углов равен 90 ^o , а один из острых углов в два раза больше другого, мы можем рассматривать их как θ и 2θ.

Итак, мы можем написать

90 ^o + θ + 2θ = 180 ^o

3θ = 180 ^o – 90 ^o

3θ = 90 ^о

θ = 90 ^о /3 = 30 ^или

2θ = 2 × 30 ^o = 60 ^o

Итак, углы равны 30 ^o , 60 ^{o 9 0304} , и 90 ^или .

Вопрос 3. Найдите значение угла подъема лестницы длиной 5 м, если основание лестницы находится на расстоянии 3 м от стены.

Решение:

Поскольку лестница действует как гипотенуза прямоугольного треугольника, а расстояние до основания равно 3 м, мы можем написать

Гипотенуза = 5 м

Основание = 3 м

Пусть угол возвышения равен θ. Итак, мы можем записать

cosθ = основание / гипотенуза = 3/5

θ = cos ^-1 (3/5)

θ = 53 ^o

Таким образом, значение угла высоты 53 ^или .

Вопрос 4. Найдите значение гипотенузы, если высота равна 8 м, а угол при основании равен 30 ^o .

Решение:

Учитывая, что угол основания равен 30 ^o , а высота равна 8 м, мы можем применить функцию синуса, чтобы найти длину гипотенузы.

sin30 ^o = высота / гипотенуза

гипотенуза = высота / sin30 ^o

Поскольку значение sin30 ^o равно 1/2, мы можем написать

гипотенуза = высота / (1/2 ) = 2 × высота

Таким образом, гипотенуза = 2 × 8 = 16 м

Таким образом, длина гипотенузы равна 16 м.