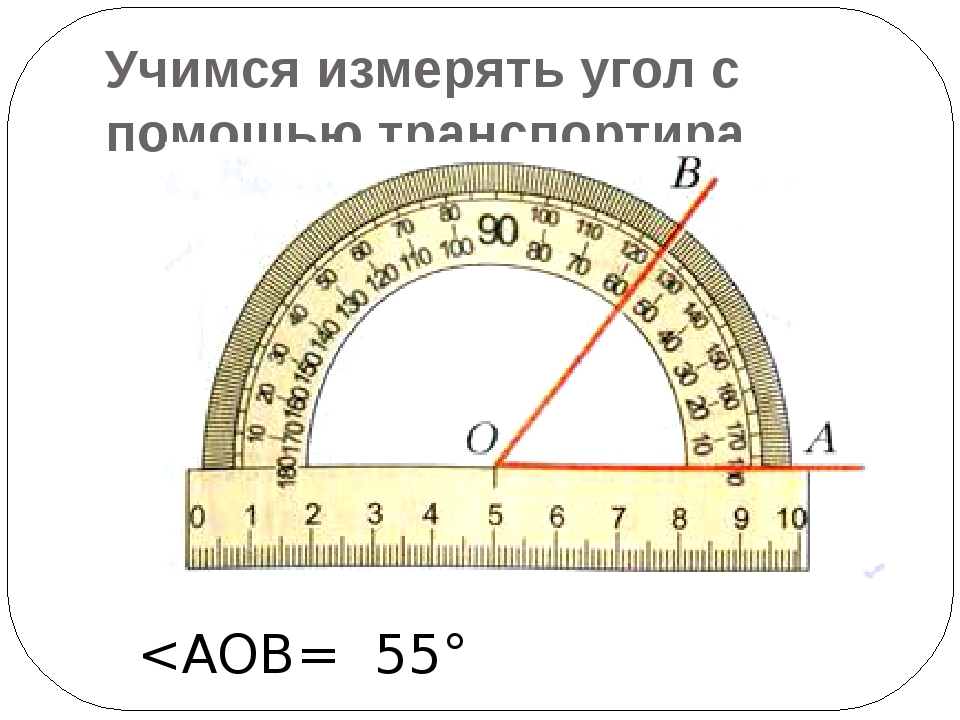
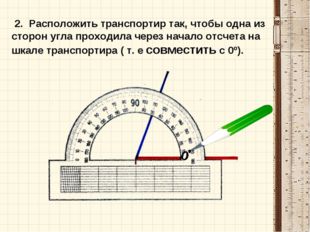
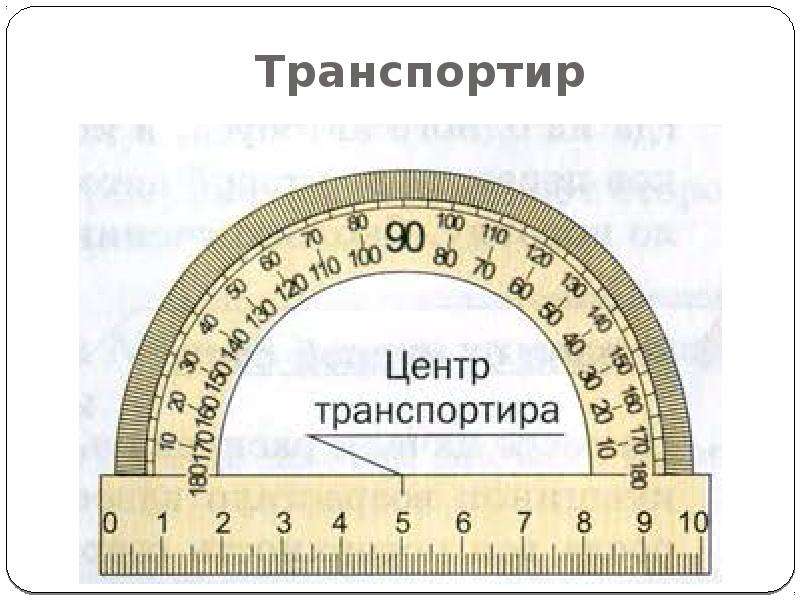
Как высчитать угол 90 градусов рулеткой
При отделочных работах и строительстве бывает нужна четкая геометрия: перпендикулярные стены и иные конструкции, требующие прямого угла в 90 градусов. Обыкновенный угольник не может позволить проверить или разметить углы со сторонами в несколько метров. Описываемый же метод превосходно подходит для разметки или проверки любых углов — длинна сторон не ограничена. Основной инструмент для измерений — рулетка.
Мы будем рассматривать точную разметку прямого угла, а также метод проверки уже размеченных углов на стенах и других объектах.
Теорема Пифагора
Теорема основана на утверждении, что у прямоугольного треугольника сумма квадратов длин катетов равна квадрату длины гипотенузы. В виде формулы записывается это так:
Стороны a и b — катеты, между которыми угол равен ровно 90 градусов. Следовательно, сторона c — гипотенуза. Подставляя в эту формулу две известные величины, мы можем вычислить третью, неизвестную. А следовательно можем размечать прямые углы, а также проверять их.
А следовательно можем размечать прямые углы, а также проверять их.
Теорема Пифагора известна еще под названием «египетский треугольник». Это треугольник со сторонами 3, 4 и 5, причем совершенно не важно, в каких единицах длинны. Между сторонами 3 и 4 — ровно девяносто градусов. Проверим данное утверждение вышеприведенной формулой: a²+b²=c² = (3×3)+(4×4) = 9+16 = (5×5) = 25 — все сходится!
А теперь применим теорему на практике.
Проверка прямого угла
Начнем с самого простого — проверки прямого угла с помощью теоремы Пифагора. Самым частым примером в отделке и строительстве является проверка перпендикулярности стен. Перпендикулярные стены — это стены, расположенные друг к другу под прямым углом 90°.
Итак, берем любой проверяемый внутренний угол. На стенах (на одной высоте) или на полу отмечаем на обоих стенах отрезки произвольных длин. Длинна этих отрезков произвольная, по возможности нужно отмечать как можно больше, но чтобы между отметками на стенах удобно было мерить диагональ. Например, мы отметили 2,5 метра (или 250 см.) на одной стене и 3 метра (или 300 см.) на другой. Теперь длину отрезка каждой стены возводим в квадрат (умножаем саму на себя) и получившиеся произведения складываем. Выглядит это так: (2,5×2,5)+(3×3)=15,25 — это диагональ в квадрате. Теперь нужно извлечь из этого числа квадратный корень √15,25≈3,90 — 3,9 метра должна составлять диагональ между нашими отметками. Если измерение рулеткой показывает другую длину диагонали — проверяемый угол развернут и имеет отклонение от 90°.
Например, мы отметили 2,5 метра (или 250 см.) на одной стене и 3 метра (или 300 см.) на другой. Теперь длину отрезка каждой стены возводим в квадрат (умножаем саму на себя) и получившиеся произведения складываем. Выглядит это так: (2,5×2,5)+(3×3)=15,25 — это диагональ в квадрате. Теперь нужно извлечь из этого числа квадратный корень √15,25≈3,90 — 3,9 метра должна составлять диагональ между нашими отметками. Если измерение рулеткой показывает другую длину диагонали — проверяемый угол развернут и имеет отклонение от 90°.
Калькулятор расчета диагонали прямого угла
Извлечение квадратного корня никогда меня не привлекало — простому человеку не обойтись без калькулятора, к тому же, не на всех мобильных устройствах калькуляторы умеют извлекать его. Поэтому можно пользоваться упрощенным методом. Нужно лишь запомнить: у прямого угла со сторонами ровно 100 сантиметров, диагональ равна 141,4 см. Таким образом, у прямого угла со сторонами 2 м. — диагональ равна 282,8 см. То есть на каждый метр плоскости приходится 141,4 см. У этого метода один недостаток: от измеряемого угла нужно откладывать одинаковые расстояния на обеих стенах и отрезки эти должны быть кратны метру. Не буду утверждать, но по моей скромной практике — это гораздо удобнее. Хотя не стоит забывать о первоначальном способе совсем — в некоторых случаях он очень актуален.
То есть на каждый метр плоскости приходится 141,4 см. У этого метода один недостаток: от измеряемого угла нужно откладывать одинаковые расстояния на обеих стенах и отрезки эти должны быть кратны метру. Не буду утверждать, но по моей скромной практике — это гораздо удобнее. Хотя не стоит забывать о первоначальном способе совсем — в некоторых случаях он очень актуален.
Сразу же возникает вопрос: какое отклонение от вычисленной длинны диагонали считать нормой (погрешностью), а какое нет? Если проверяемый угол с отмеченными сторонами по 1 м. будет 89°, то диагональ уменьшится до 140 см. Из понимания этой зависимости можно сделать объективный вывод, что погрешность диагонали 141,4 см. в несколько миллиметров не даст отклонения в один целый градус.
Как проверить внешний угол? Проверка внешнего угла по сути не отличается, нужно лишь продлить линии каждой стены на полу (или земле, при помощи шнура) и получившийся внутренний угол измерить обычным способом.
Как разметить прямой угол рулеткой
Разметка может основываться как на общей теореме Пифагора, так и на принципе «египетского треугольника». Однако это только в теории линии просто чертятся на бумаге, «ловить» же все выбранные размеры растянутыми шнурами или линиями на полу — задача посложнее.
Однако это только в теории линии просто чертятся на бумаге, «ловить» же все выбранные размеры растянутыми шнурами или линиями на полу — задача посложнее.
Поэтому я предлагаю упрощенный способ, основанный на диагонали 141,4 см. у треугольника со сторонами 100 см. Вся последовательность разметки изображена на картинках ниже. Важно не забывать: диагональ 141,4 см. нужно умножать на количество метров в отрезке А-Б. Отрезки А-Б и А-В должны быть равны и соответствовать целому числу в метрах. Картинки увеличиваются по клику!
Как разметить острый угол
Гораздо реже возникает надобность в создании острых углов, в частности 45°. Для формирования подобных фигур формулы более сложные, однако это не самое проблематичное. Гораздо сложнее свести все линии, начерченные или натянутые шнурами — дело это непростое. Поэтому я предлагаю использовать упрощенный метод. Сначала размечается прямой угол 90°, а затем диагональ 141,4 делится на нужное количество равных частей. Например, чтобы получить 45°, диагональ нужно поделить пополам и от точки А провести линию через место деления. Таким образом мы получим два угла по 45 градусов. Если поделить диагональ на 3 части, то получится три угла по 30 градусов. Думаю алгоритм вам понятен.
Таким образом мы получим два угла по 45 градусов. Если поделить диагональ на 3 части, то получится три угла по 30 градусов. Думаю алгоритм вам понятен.
Собственно я рассказал все, что мог рассказать, надеюсь все изложил понятным языком и у вас больше не возникнет вопросов как размечать и проверять прямые углы. Стоит добавить, что уметь делать это должен любой отделочник или строитель, ведь полагаться на строительный угольник небольшого размера — непрофессионально.
При ремонте, строительстве или самостоятельном изготовлении мебели часто бывает необходимо проверить или построить прямой угол. В любом случае, очень важна точность измерения, но если стороны угла равны нескольким метрам, то это сложно будет сделать с помощью угольника. Сегодня мы рассмотрим несколько универсальных методов замера прямого угла с помощью рулетки.
Теорема Пифагора
Проверить прямой угол поможет известная каждому со школьных времен теорема Пифагора. Вспомним определение: ”В прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов” ( a 2 + b 2 = с 2 ), где a и b – катеты, а с – гипотенуза. Подставив в формулу известные нам две величины, получим неизвестную третью.
Подставив в формулу известные нам две величины, получим неизвестную третью.
А теперь вернемся к нашим замерам и применим теорему на практике.
Для того, чтобы проверить угол, отмечаем на обеих стенах произвольные отрезки, желательно отмерять их побольше, чтобы удобнее было отмерять диагональ между ними. После того, как вы отметили эти отрезки, возведите длину каждого в квадрат и сложите. Из полученного результата извлеките квадратный корень (для удобства можно воспользоваться калькулятором). Теперь замеряем рулеткой длину диагонали между двумя отрезками, она должна совпадать с полученным результатом. Если в результате измерения получилось другое число, то угол не равен 90 градусов.
Египетский треугольник
Также не стоит забывать и о такой геометрической фигуре, как египетский треугольник – прямоугольник с длинами сторон 3, 4, 5, причем совершенно не важно в каких величинах, ведь между катетами длиной 3 и 4 угол, равный ровно 90 градусов. Давайте проверим?
a 2 + b 2 = (3 2 + 4 2 ) = (9 + 16) = 25; √25 = 5.
Как проверить угол с помощью египетского треугольника?
Отмерьте на одной стене отрезок длиной 3 метра, а на другой – отрезок длиной 4 метра. Теперь измеряем расстояние между двумя этими отметками точно так же, как в способе с теоремой Пифагора. Если получившийся результат кратен 5, то в том, что полученный угол равен 90 градусов, можно не сомневаться.
Как отмерить угол, используя рулетку
Можно самостоятельно смастерить угольник для замера углов:
- Соединяем две рейки одна перпендикулярно другой.
- Измеряем на одной рейке 60 см, на другой 80, лишнее обрезаем.
- Прибиваем третью рейку к одной отметке.
- Измеряем гипотенузу, прибиваем рейку ко второй метке.
- Еще раз проверяем размеры и при необходимости фиксируем ещё в нескольких местах.
- Обрезаем лишние концы.
Как видите, знание нескольких простых школьных теорем может помочь и в строительстве, и в ремонте. Зная несколько простых хитростей, вы всегда с легкостью можете создать или проверить прямой угол.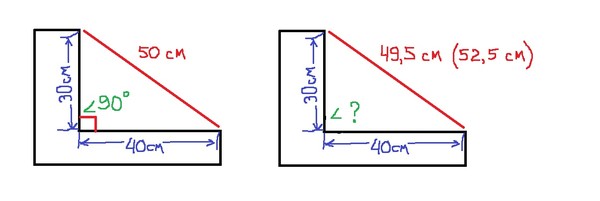
Строительная рулетка для электрика является таким же обязательным инструментом, как и индикатор напряжения. Даже у тех профессионалов, которые имеют в комплекте инструмента осепостроители и лазерные дальномеры, непременно в подсумке всегда присутствует обыкновенная рулетка.
Без нее не обойтись ни при разметке трасс электропроводки, ни при монтаже подрозетников.
Однако далеко не каждый знаком со всеми секретами и дополнительными возможностями при использовании строительной рулетки.
У нее оказывается очень много скрытых способностей, которые помогут вам заменить сразу несколько инструментов и значительно сэкономить время на ремонт.
Кстати, один из важных советов, для тех кто пользуется китайскими дешевыми рулетками заключается в следующем — если у вас именно такой экземпляр, то старайтесь все замеры делать одной рулеткой.
Один и тот же размер при измерении разными рулетками может не совпадать.
Один знакомый измерял расстояние стен в доме китайским инструментом, а в магазине при покупке материалов воспользовался их рулеткой.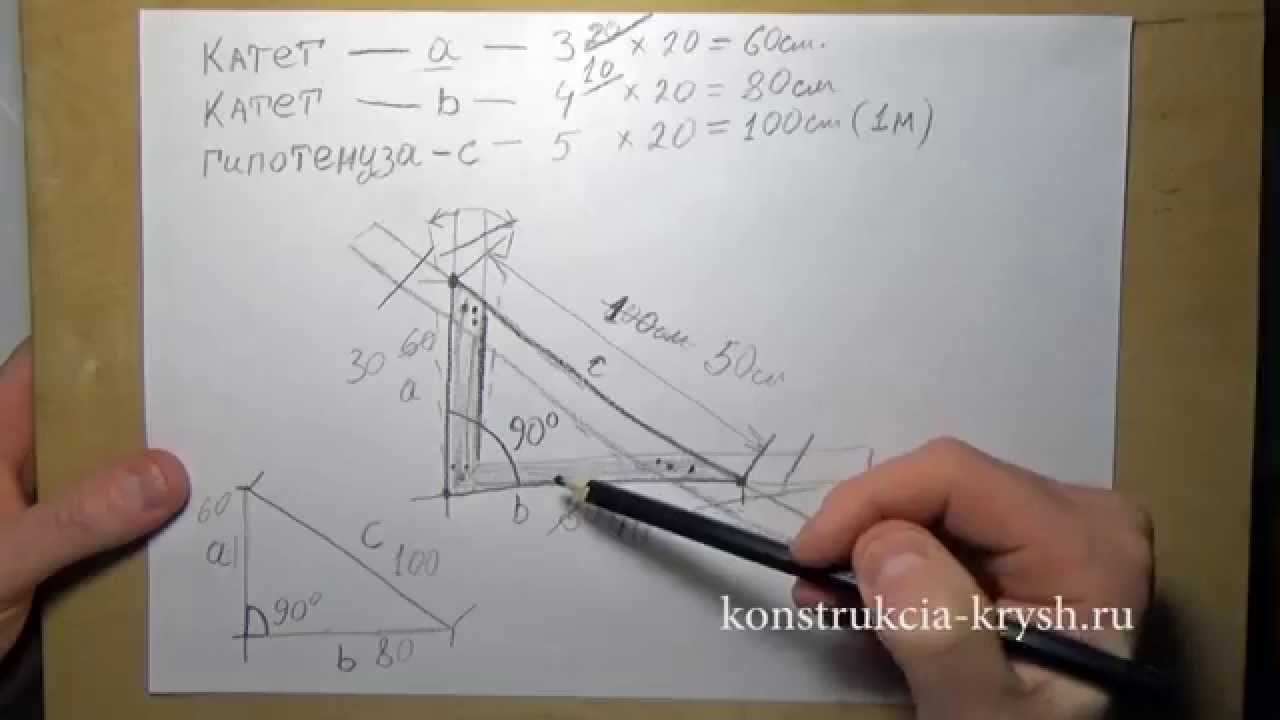 В итоге, дома очень был удивлен результатом покупки.
В итоге, дома очень был удивлен результатом покупки.
Подвижный зацеп сегодня встречается почти на каждой рулетке. И эта штука вовсе не для того, чтобы удобно спину почесать 🙂
Новички вообще нередко думают, что это какой-то брак. Какая в итоге будет точность, если один из ключевых элементов болтается и не закреплен надежно? Некоторые даже умудряются его заклепать сразу же после покупки.
Оказывается, что подвижный зацеп это необходимость, без которой вообще не возможна нормальная работа.
Объясняется это тем, что измерения рулеткой можно производить двумя способами:
- от предмета
Когда вы измеряете расстояние от предмета, зацеп выполняет роль нулевой точки. При измерении с захватом предмета, зацеп выдвигается на свою толщину. Тем самым нулевая отметка снова совпадает с краем предмета.
Поэтому не стоит сматывать строительную рулетку с эффектным щелчком в конце, тем самым вы только сократите срок ее службы.
Еще во многих моделях лента рулетки в самом начале на расстоянии 2,5см имеет отверстие. Сделано оно не просто так, а опять же чтобы облегчить вашу работу в одиночку.
Сделано оно не просто так, а опять же чтобы облегчить вашу работу в одиночку.
Когда не за что закрепиться зацепом или неудобно им пользоваться из-за косой поверхности, простым шилом или гвоздиком через отверстие намертво закрепляете ленту и растягиваете ее на любую длину.
Воспользовавшись таким отверстием в рулетке вам не придется применять подобные захваты как на фото ниже. А всю работу по разметке можно легко проделывать без напарника.
Как вы понимаете при замерах в углах, серединой ленты рулетки очень трудно залезть непосредственно в угол. Также неудобно делать точные измерения в дверном или оконном проеме.
Поэтому в том случае когда нужно замерить проем, используйте корпус как продолжение рулетки.
На внешней стороне самой рулетки указан размер корпуса, который и нужно прибавить к показаниям ленты при измерении.
Если такого размера на корпус не нанесено, никто вам не мешает самостоятельно его измерить и написать в любом удобном месте.
Есть еще способ сделать подобные замеры с применением малярной ленты. Наклеиваете на поверхность кусочек ленты и производите два измерения в противоположных направлениях.
Наклеиваете на поверхность кусочек ленты и производите два измерения в противоположных направлениях.
При этом карандашом в качестве метки лучше ставить галочки, а не простые черточки. Они будут визуально точнее показывать отметку. Тогда как черточка может быть нарисована криво, что и вызовет погрешность.
Проделав два измерения нужно сложить результаты и получите точный размер.
На многих зацепах рулетка имеет небольшое отверстие. Этим отверстием удобно зацепиться за шуруп или гвоздь. После этого зацеп уже никуда не соскочит.
Особенно это полезно, когда вы в одиночку проводите измерения на больших расстояниях. Погрешность измерения при этом будет не более 1-2мм, так как центр шурупа находится практически на нулевой отметке ленты.
Еще при помощи этого разъема в зацепе очень удобно рисовать окружности. Не нужно при себе иметь ни циркуля, ни транспортира.
В некоторых моделях зацепы выполняют магнитными. Помимо прямого их назначения, такими зацепами удобно поднимать упавшие предметы не слезая со стремянки.
Если применить небольшую доработку к дешевой рулетке, то из одного инструмента получается отличное приспособление для разметки.
Берете ножку циркуля, которая применяется с простыми карандашами, и закрепляете ее на внешней стороне рулетки.
Эту конструкцию можно сделать съемной, или вообще приспособить под отдельную рулетку.
Таким устройством очень удобно делать различные отметки или пользоваться им как рейсмусом.
А при использовании шурупа легко рисуются окружности нужного диаметра.
Если вы работаете с гипсокартоном или другой поверхностью, которую можно безопасно поцарапать, то рулетку стоит переделать под еще одну возможность. Надфилем на зацепе делаете зазубрины.
После чего с помощью этого зацепа легко делаются отметки на поверхности. При этом уже даже не обязательно чтобы под рукой был карандаш.
Внешнюю часть рулетки легко превратить в мини напоминалку или поверхность для записей. Берете малярную ленту и наклеиваете сбоку рулетки.
Если нет под рукой малярки, то можно писать прямо на самом корпусе.
Правда для этого, сначала надо пройтись по поверхности наждачкой нулевкой.
Так вы сделаете ее несколько бархатной, после чего надписи будут наноситься горазд легче.
Писать конечно нужно карандашом, после чего все это легко стирается резинкой.
С помощью строительной рулетки очень легко разделить любое число с точность до миллиметра пополам, не прибегая к услугам калькулятора.
Берете размер на рулетке, к примеру 116см — и сложив ленту пополам совмещаете с ним нулевую отметку, там где верхний зацеп.
Ровно в месте перегиба и будет требуемый результат — 58см.
Этим же способом можно не только делить, но и отнимать. Например общая длина стенки у вас 2м 11см, а распредкоробка находится от первого края на расстоянии в 1м 38см. Вам нужно быстро узнать сколько остается от этой распредкоробки до другого края стены, чтобы отмерить кабель канал.
Вытягиваете ленту на 2м 11см и складываете ее пополам.
Затем ищете отметку в 1м 38см. Как раз напротив нее, на второй половине ленты, и будет показано нужное вам расстояние — 73см.
Используя обыкновенную ленту рулетки можно легко разделить рабочую поверхность или заготовку на требуемое количество равных частей. Данный метод подходит в первую очередь для больших поверхностей — для труб или кабель каналов уже не сработает.
Как вы поступаете обычно? Замеряете общую длину или ширину, затем делаете вычисления и делите расстояние на нужное количество частей. После чего вновь линейкой или рулеткой отмеряете на поверхности эти части.
Оказывается все это можно проделать без калькулятора и даже без вычислений. Берете на рулетке число, которое больше чем ширина заготовки, и при этом кратно той величине, на которое вы хотите разделить расстояние.
Например ширина доски 17см, а вам ее нужно разделить на четыре равные части. Сдвигаете рулетку по диагонали до ближайшей отметки в 20см. После чего легко делите эти 20см на 4 и отмечаете метки на расстояниях 5см, 10см, 15см, 20см.
В итоге вы всего одним движением рулетки разделили поверхность на нужное количество частей.
Захотели поделить на 6 частей — ничего сложного. Можно сдвинуть диагональ до 30см и проделать то же самое.
Еще рулеткой на круглой трубе можно точно отмерить поперечный срез. Для этого плотно прижимаете по периметру трубы ленту, совместив концы. Если совместили ровно, никак иначе как под углом в 90 градусов она не ляжет.
Чем шире лента рулетки, тем предпочтительней. Проделать такой же фокус можно и с простым листком бумаги.
Когда невозможно измерить диаметр трубы или заготовки с торца, опять поможет строительная рулетка и геометрия. Обхватываете трубу лентой и измеряете ее окружность. После чего полученный результат нужно разделить на число Пи = 3,14. Это и будет необходимый диаметр.
Еще раз применив знания геометрии, строительной рулеткой без угольников и других инструментов можно проверить точность прямого угла. Как вы знаете из школьного курса — сумма квадратов катетов прямоугольного треугольника равна квадрату гипотенузы.
Берете любую поверхность где должен быть прямой угол, например две стены комнаты. Отмеряете рулеткой в одну сторону 30см, а в другую 40см и ставите метки. Если угол действительно прямой и строители не накосячили, то соединив эти две метки по гипотенузе, вы должны получить на рулетке расстояние ровно в 50см.
Такой метод применим к любым поверхностям и изделиям. Главное что вам нужно соблюдать при измерении — это пропорции 3 -4 -5.
Если вы еще не приобрели себе рулетку, подобрать необходимую модель и ознакомиться с текущими ценами на них можно здесь.
Как проверить прямой угол без угольника
При отделочных работах и строительстве бывает нужна четкая геометрия: перпендикулярные стены и иные
конструкции, требующие прямого угла в 90 градусов. Обыкновенный угольник не может позволить проверить или
разметить углы со сторонами в несколько метров. Описываемый же метод превосходно подходит для разметки или
Описываемый же метод превосходно подходит для разметки или
проверки любых углов — длинна сторон не ограничена. Основной инструмент для измерений — рулетка.
Мы будем рассматривать точную разметку прямого угла, а также метод проверки уже размеченных углов на стенах
и других объектах.
Теорема Пифагора
Теорема основана на утверждении, что у прямоугольного треугольника сумма квадратов длин катетов равна
квадрату длины гипотенузы. В виде формулы записывается это так:
a²+b²=c²
Стороны a и b — катеты, между которыми угол равен ровно 90 градусов. Следовательно, сторона c — гипотенуза.
Подставляя в эту формулу две известные величины, мы можем вычислить третью, неизвестную. А следовательно можем
размечать прямые углы, а также проверять их.
Теорема Пифагора известна еще под названием «египетский треугольник». Это треугольник со сторонами 3, 4 и 5,
причем совершенно не важно, в каких единицах длинны. Между сторонами 3 и 4 — ровно девяносто градусов. Проверим
данное утверждение вышеприведенной формулой: a²+b²=c² = (3×3)+(4×4) = 9+16 = (5×5) = 25 — все
сходится!
А теперь применим теорему на практике.
Проверка прямого угла
Начнем с самого простого — проверки прямого угла с помощью теоремы Пифагора. Самым частым примером
в отделке и строительстве является проверка перпендикулярности стен. Перпендикулярные стены —
это стены, расположенные друг к другу под прямым углом 90°.
Итак, берем любой проверяемый внутренний угол. На стенах (на одной высоте) или на полу отмечаем на обоих
стенах отрезки произвольных длин. Длинна этих отрезков произвольная, по возможности нужно отмечать как можно
Длинна этих отрезков произвольная, по возможности нужно отмечать как можно
больше, но чтобы между отметками на стенах удобно было мерить диагональ. Например, мы отметили 2,5 метра (или 250
см.) на одной стене и 3 метра (или 300 см.) на другой. Теперь длину отрезка каждой стены возводим в квадрат
(умножаем саму на себя) и получившиеся произведения складываем. Выглядит это так: (2,5×2,5)+(3×3)=15,25 —
это диагональ в квадрате. Теперь нужно извлечь из этого числа квадратный корень √15,25≈3,90 — 3,9 метра
должна составлять диагональ между нашими отметками. Если измерение рулеткой показывает другую длину диагонали —
проверяемый угол развернут и имеет отклонение от 90°.
Калькулятор расчета диагонали прямого угла
Извлечение квадратного корня никогда меня не привлекало — простому человеку не обойтись без калькулятора, к тому же,
не на всех мобильных устройствах калькуляторы умеют извлекать его. Поэтому можно пользоваться упрощенным методом. Нужно
Поэтому можно пользоваться упрощенным методом. Нужно
лишь запомнить: у прямого угла со сторонами ровно 100 сантиметров, диагональ равна 141,4 см. Таким образом, у
прямого угла со сторонами 2 м. — диагональ равна 282,8 см. То есть на каждый метр плоскости приходится 141,4 см. У этого
метода один недостаток: от измеряемого угла нужно откладывать одинаковые расстояния на обеих стенах и отрезки эти должны
быть кратны метру. Не буду утверждать, но по моей скромной практике — это гораздо удобнее. Хотя не стоит забывать
о первоначальном способе совсем — в некоторых случаях он очень актуален.
Сразу же возникает вопрос: какое отклонение от вычисленной длинны диагонали считать нормой (погрешностью), а какое
нет? Если проверяемый угол с отмеченными сторонами по 1 м. будет 89°, то диагональ уменьшится до 140 см. Из
понимания этой зависимости можно сделать объективный вывод, что погрешность диагонали 141,4 см. в несколько миллиметров
в несколько миллиметров
не даст отклонения в один целый градус.
Как проверить внешний угол? Проверка внешнего угла по сути не отличается, нужно лишь продлить линии каждой стены
на полу (или земле, при помощи шнура) и получившийся внутренний угол измерить обычным способом.
Как разметить прямой угол рулеткой
Разметка может основываться как на общей теореме Пифагора, так и на принципе «египетского треугольника». Однако
это только в теории линии просто чертятся на бумаге, «ловить» же все выбранные размеры растянутыми шнурами или
линиями на полу — задача посложнее.
Поэтому я предлагаю упрощенный способ, основанный на диагонали 141,4 см. у треугольника со сторонами 100 см. Вся
последовательность разметки изображена на картинках ниже. Важно не забывать: диагональ 141,4 см. нужно умножать на
нужно умножать на
количество метров в отрезке А-Б. Отрезки А-Б и А-В должны быть равны и соответствовать целому числу в метрах.
Картинки увеличиваются по клику!
Как разметить острый угол
Гораздо реже возникает надобность в создании острых углов, в частности 45°. Для формирования подобных
фигур формулы более сложные, однако это не самое проблематичное. Гораздо сложнее свести все линии, начерченные
или натянутые шнурами — дело это непростое. Поэтому я предлагаю использовать упрощенный метод. Сначала размечается
прямой угол 90°, а затем диагональ 141,4 делится на нужное количество равных частей. Например, чтобы получить
45°, диагональ нужно поделить пополам и от точки А провести линию через место деления. Таким образом мы получим
два угла по 45 градусов. Если поделить диагональ на 3 части, то получится три угла по 30 градусов. Думаю алгоритм
вам понятен.
Собственно я рассказал все, что мог рассказать, надеюсь все изложил понятным языком и у вас больше не возникнет
вопросов как размечать и проверять прямые углы. Стоит добавить, что уметь делать это должен любой отделочник или
строитель, ведь полагаться на строительный угольник небольшого размера — непрофессионально.
Оцените публикацию:
Оценка: 4.3 (105 голосов)
Смотрите также другие статьи
Как отмерить прямой угол с помощью рулетки
При ремонте, строительстве или самостоятельном изготовлении мебели часто бывает необходимо проверить или построить прямой угол. В любом случае, очень важна точность измерения, но если стороны угла равны нескольким метрам, то это сложно будет сделать с помощью угольника. Сегодня мы рассмотрим несколько универсальных методов замера прямого угла с помощью рулетки.
Сегодня мы рассмотрим несколько универсальных методов замера прямого угла с помощью рулетки.
Теорема Пифагора
Проверить прямой угол поможет известная каждому со школьных времен теорема Пифагора. Вспомним определение: »В прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов» ( a2 + b2 = с2 ), где a и b — катеты, а с — гипотенуза. Подставив в формулу известные нам две величины, получим неизвестную третью.
А теперь вернемся к нашим замерам и применим теорему на практике.
Для того, чтобы проверить угол, отмечаем на обеих стенах произвольные отрезки, желательно отмерять их побольше, чтобы удобнее было отмерять диагональ между ними. После того, как вы отметили эти отрезки, возведите длину каждого в квадрат и сложите. Из полученного результата извлеките квадратный корень (для удобства можно воспользоваться калькулятором). Теперь замеряем рулеткой длину диагонали между двумя отрезками, она должна совпадать с полученным результатом. Если в результате измерения получилось другое число, то угол не равен 90 градусов.
Если в результате измерения получилось другое число, то угол не равен 90 градусов.
Египетский треугольник
Также не стоит забывать и о такой геометрической фигуре, как египетский треугольник — прямоугольник с длинами сторон 3, 4, 5, причем совершенно не важно в каких величинах, ведь между катетами длиной 3 и 4 угол, равный ровно 90 градусов. Давайте проверим?
a2 + b2 = (32 + 42) = (9 + 16) = 25; √25 = 5.
Как проверить угол с помощью египетского треугольника?
Отмерьте на одной стене отрезок длиной 3 метра, а на другой — отрезок длиной 4 метра. Теперь измеряем расстояние между двумя этими отметками точно так же, как в способе с теоремой Пифагора. Если получившийся результат кратен 5, то в том, что полученный угол равен 90 градусов, можно не сомневаться.
Как отмерить угол, используя рулетку
Можно самостоятельно смастерить угольник для замера углов:
- Соединяем две рейки одна перпендикулярно другой.

- Измеряем на одной рейке 60 см, на другой 80, лишнее обрезаем.
- Прибиваем третью рейку к одной отметке.
- Измеряем гипотенузу, прибиваем рейку ко второй метке.
- Еще раз проверяем размеры и при необходимости фиксируем ещё в нескольких местах.
- Обрезаем лишние концы.
Как видите, знание нескольких простых школьных теорем может помочь и в строительстве, и в ремонте. Зная несколько простых хитростей, вы всегда с легкостью можете создать или проверить прямой угол.
Египетский треугольник. Прямой угол без инструмента. |
15.01.2016 profipol_dp
3 710 просмотра
Как выставить угол 90 градусов без специального инструмента (угольника)?
Допустим, у нас есть линия к которой нам нужно выставить перпендикуляр, т.е. еще одну линию под углом 90 градусов относительно первой. Или у нас есть угол (например, угол комнаты) и нам нужно проверить равен ли он 90 градусам.
Все это можно сделать с помощью одной только рулетки и карандаша.
Есть две отличные штуки, такие как «Египетский треугольник» и теорема Пифагора, которые нам в этом помогут.
Итак, Египетский треугольник — это прямоугольный треугольник с соотношением всех сторон равным 3:4:5 (катет 3: катет 4: гипотенуза 5).
Египетский треугольник напрямую связан с теоремой Пифагора — сумма квадратов катетов равна квадрату гипотенузы (3*3 + 4*4 = 5*5).
Как нам это может помочь? Все очень просто.
Задача №1. Нужно построить перпендикуляр к прямой линии (например, линию под 90 градусов к стене).
Шаг 1. Для этого от точки №1 (где будет наш угол) нужно отмерить на этой линии любое расстояние кратное трем или четырем — это будет наш первый катет (равный трем или четырем частям, соответственно), получаем точку №2.
Для простоты вычислений можно взять расстояние, например 2м (это 4 части по 50см).
Шаг 2. Затем от этой же точки №1 отмеряем 1,5м (3 части по 50см) вверх (выставляем примерный перпендикуляр), чертим линию (зеленая).
Шаг 3. Теперь из точки №2 нужно поставить метку на зеленой линии на расстоянии 2,5м (5 частей по 50см). Пересечение этих меток и будет нашей точкой №3.
Соединив точки №1 и №3 мы получим линию-перпендикуляр нашей первой линии.
Задача №2. Вторая ситуация — есть угол и нужно проверить прямой ли он.
Вот он, наш угол. Крнечно проще проверить большим угольником. А если его нет?
Отмеряем от угла любую длину кратную четырем, в данном случае это 1,6м.
В другую сторону три части, соответственно 1,2м.
И между этими точками должно оказаться пять частей, т.е. 2м.
Как видите, у нас угол оказался прямее всех прямых.
Чего и вам желаем!
Это тоже интересно:
инструмент, разметка укладки кафеля,
Как отмерить угол 90 градусов рулеткой. Как разметить фундамент. Строительный лайфхак своими руками.
 Исправляем ошибку кроя
Исправляем ошибку кроя
Часто домашнему мастеру необходимо срочно произвести какое либо измерение или сделать разметку под определенным углом, а под рукой нет либо угольника, либо транспортира. В этом случае его выручат несколько простых правил.
Угол 90 градусов.
Если нужно срочно построить прямой угол, а угольника нет, можно воспользоваться любым печатным изданием. Угол бумажного листа — очень точный прямой угол (90 град.). Резательные (вырубочные) машины в типографиях настроены очень точно. Иначе исходный рулон бумаги начнет резаться вкривь и вкось. Поэтому вы можете быть уверены, что этот угол — именно прямой.
А если нет даже печатного издания или необходимо построить угол на местности, например при разметке фундамента или листа фанеры с неровными краями? В этом случае нам поможет правило золотого (или египетского) треугольника.
Золотым (или египетским, или Пифагоровым) треугольником называется треугольник со сторонами, которые соотносятся друг с другом как 5:4:3. По теореме Пифагора, у прямоугольного треугольника квадрат гипотенузы равен сумме квадратов катетов. Т.е. 5х5 = 4х4 + 3х3. 25=16+9 и это неоспоримо.
По теореме Пифагора, у прямоугольного треугольника квадрат гипотенузы равен сумме квадратов катетов. Т.е. 5х5 = 4х4 + 3х3. 25=16+9 и это неоспоримо.
Поэтому для построения прямого угла достаточно на заготовке провести прямую линию длиной 5 (10,15,20 и т.д. кратной 5 см). А затем, из краев этой линии начать отмерять с одной стороны 4 (8,12,16 и т.д кратно 4 см), а с другой — 3 (6,9,12,15 и т.д. кратно 3 см) расстояния. Должны получиться дуги с радиусом 4 и 3 см. Где эти дуги пересекутся между собой и будет прямой (90 градусов) угол.
Угол 45 градусов.
Такие углы обычно применяют при изготовлении прямоугольных рамок. Материал из которого делается рамка (багет) пилится под углом 45 градусов и стыкуется. Если под рукой нет стусла или транспортира, получить шаблон угла в 45 градусов можно следующим образом. Необходимо взять лист писчей бумаги или любого печатного издания и согнуть его так, что бы линия сгиба проходила точно через угол, а края загнутого листа совпадали. Получившийся угол и будет равен 45 градусам.
Получившийся угол и будет равен 45 градусам.
Угол 30 и 60 градусов.
Угол в 60 градусов требуется для построения равносторонних треугольников. Например, вам надо напилить такие треугольники для декоративных работ или точно установить силовой укос. Угол в 30 градусов редко применяется в чистом виде. Однако с его помощью (и с помощью угла в 90 градусов) строится угол 120 градусов. А это угол, необходимый для построения равносторонних шестиугольников, фигуры весьма популярной у столяров.
Для построения весьма точного шаблона этих углов в любой момент необходимо запомнить константу (число) 173. Они вытекает из соотношений синусов и косинусов этих углов.
Возьмите лист бумаги из любого печатного издания. Его угол равен точно 90 градусам. От угла по одной стороне отмерьте 100 мм (10 см.), а по другой — 173 мм (17,3 см). Соедините эти точки. Таким образом мы и получили шаблон, у которого один угол 90 градусов, один 30 градусов и один 60 градусов. Можете проверить на транспортире — все точно!
Запомните это число — 173, и вы всегда сможете построить углы в 30 и 60 градусов.
Прямоугольность заготовки.
При разметке заготовок или построений на деталях кроме самих углов весьма важно и их соотношение. Особенно это важно при изготовлении прямоугольных деталей или например при разметке фундамента, раскрое больших листов материала. Неправильное построение или разметка приносит впоследствии много лишней работы или к появлению большого числа отходов.
К сожалению, даже весьма точные разметочные инструменты, даже профессиональные, всегда имеют определенную погрешность.
Между тем, существует весьма простой метод определения прямоугольности детали или построения. В прямоугольнике диагонали абсолютно равны! Значит, после построения необходимо измерить длины диагоналей прямоугольника. Если они равны, все в порядке, это действительно прямоугольник. А если нет — вы построили параллелограмм или ромб. В этом случае следует немного «поиграть» смежными сторонами, что бы добиться точного (для данного случая) равенства диагоналей размечаемого прямоугольника.
Строительная рулетка для электрика является таким же обязательным инструментом, как и индикатор напряжения. Даже у тех профессионалов, которые имеют в комплекте инструмента осепостроители и лазерные дальномеры, непременно в подсумке всегда присутствует обыкновенная рулетка.
Без нее не обойтись ни при разметке трасс электропроводки, ни при монтаже подрозетников.
Однако далеко не каждый знаком со всеми секретами и дополнительными возможностями при использовании строительной рулетки.
У нее оказывается очень много скрытых способностей, которые помогут вам заменить сразу несколько инструментов и значительно сэкономить время на ремонт.
Кстати, один из важных советов, для тех кто пользуется китайскими дешевыми рулетками заключается в следующем — если у вас именно такой экземпляр, то старайтесь все замеры делать одной рулеткой.
Один и тот же размер при измерении разными рулетками может не совпадать.
Один знакомый измерял расстояние стен в доме китайским инструментом, а в магазине при покупке материалов воспользовался их рулеткой. В итоге, дома очень был удивлен результатом покупки.
В итоге, дома очень был удивлен результатом покупки.
Подвижный зацеп на рулетке
Подвижный зацеп сегодня встречается почти на каждой рулетке. И эта штука вовсе не для того, чтобы удобно спину почесать 🙂
Новички вообще нередко думают, что это какой-то брак. Какая в итоге будет точность, если один из ключевых элементов болтается и не закреплен надежно? Некоторые даже умудряются его заклепать сразу же после покупки.
Оказывается, что подвижный зацеп это необходимость, без которой вообще не возможна нормальная работа.
Объясняется это тем, что измерения рулеткой можно производить двумя способами:
Когда вы измеряете расстояние от предмета, зацеп выполняет роль нулевой точки. При измерении с захватом предмета, зацеп выдвигается на свою толщину. Тем самым нулевая отметка снова совпадает с краем предмета.
Точность измерения при этом как раз таки не страдает, а наоборот соблюдается.
Правда следует сделать справедливое замечание — подвижный зацеп со временем разбивается и может появиться погрешность до пары миллиметров.
Происходит это из-за постоянных ударов зацепа при закрытии.
Поэтому не стоит сматывать строительную рулетку с эффектным щелчком в конце, тем самым вы только сократите срок ее службы.
Еще во многих моделях лента рулетки в самом начале на расстоянии 2,5см имеет отверстие.
Сделано оно не просто так, а опять же чтобы облегчить вашу работу в одиночку.
Когда не за что закрепиться зацепом или неудобно им пользоваться из-за косой поверхности, простым шилом или гвоздиком через отверстие намертво закрепляете ленту и растягиваете ее на любую длину.
Воспользовавшись таким отверстием в рулетке вам не придется применять подобные захваты как на фото ниже.
А всю работу по разметке можно легко проделывать без напарника.
Измерения в проемах и углах
Как вы понимаете при замерах в углах, серединой ленты рулетки очень трудно залезть непосредственно в угол. Также неудобно делать точные измерения в дверном или оконном проеме.
Поэтому в том случае когда нужно замерить проем, используйте корпус как продолжение рулетки.
На внешней стороне самой рулетки указан размер корпуса, который и нужно прибавить к показаниям ленты при измерении.
Если такого размера на корпус не нанесено, никто вам не мешает самостоятельно его измерить и написать в любом удобном месте.
Есть еще способ сделать подобные замеры с применением малярной ленты. Наклеиваете на поверхность кусочек ленты и производите два измерения в противоположных направлениях.
При этом карандашом в качестве метки лучше ставить галочки, а не простые черточки. Они будут визуально точнее показывать отметку. Тогда как черточка может быть нарисована криво, что и вызовет погрешность.
Проделав два измерения нужно сложить результаты и получите точный размер.
Отверстие в зацепе
На многих зацепах рулетка имеет небольшое отверстие. Этим отверстием удобно зацепиться за шуруп или гвоздь. После этого зацеп уже никуда не соскочит.
Особенно это полезно, когда вы в одиночку проводите измерения на больших расстояниях. Погрешность измерения при этом будет не более 1-2мм, так как центр шурупа находится практически на нулевой отметке ленты.
Погрешность измерения при этом будет не более 1-2мм, так как центр шурупа находится практически на нулевой отметке ленты.
Еще при помощи этого разъема в зацепе очень удобно рисовать окружности. Не нужно при себе иметь ни циркуля, ни транспортира.
В некоторых моделях зацепы выполняют магнитными. Помимо прямого их назначения, такими зацепами удобно поднимать упавшие предметы не слезая со стремянки.
Рулетка маркер
Если применить небольшую доработку к дешевой рулетке, то из одного инструмента получается отличное приспособление для разметки.
Берете ножку циркуля, которая применяется с простыми карандашами, и закрепляете ее на внешней стороне рулетки.
Эту конструкцию можно сделать съемной, или вообще приспособить под отдельную рулетку.
Таким устройством очень удобно делать различные отметки или пользоваться им как рейсмусом.
А при использовании шурупа легко рисуются окружности нужного диаметра.
Если вы работаете с гипсокартоном или другой поверхностью, которую можно безопасно поцарапать, то рулетку стоит переделать под еще одну возможность. Надфилем на зацепе делаете зазубрины.
Надфилем на зацепе делаете зазубрины.
После чего с помощью этого зацепа легко делаются отметки на поверхности. При этом уже даже не обязательно чтобы под рукой был карандаш.
Рулетка памятка
Внешнюю часть рулетки легко превратить в мини напоминалку или поверхность для записей. Берете малярную ленту и наклеиваете сбоку рулетки.
Если нет под рукой малярки, то можно писать прямо на самом корпусе.
Правда для этого, сначала надо пройтись по поверхности наждачкой нулевкой.
Так вы сделаете ее несколько бархатной, после чего надписи будут наноситься горазд легче.
Писать конечно нужно карандашом, после чего все это легко стирается резинкой.
Рулетка калькулятор
С помощью строительной рулетки очень легко разделить любое число с точность до миллиметра пополам, не прибегая к услугам калькулятора.
Берете размер на рулетке, к примеру 116см — и сложив ленту пополам совмещаете с ним нулевую отметку, там где верхний зацеп.
Ровно в месте перегиба и будет требуемый результат — 58см.
Этим же способом можно не только делить, но и отнимать. Например общая длина стенки у вас 2м 11см, а распредкоробка находится от первого края на расстоянии в 1м 38см. Вам нужно быстро узнать сколько остается от этой распредкоробки до другого края стены, чтобы отмерить кабель канал.
Вытягиваете ленту на 2м 11см и складываете ее пополам.
Затем ищете отметку в 1м 38см. Как раз напротив нее, на второй половине ленты, и будет показано нужное вам расстояние — 73см.
Деление рулеткой на несколько частей
Используя обыкновенную ленту рулетки можно легко разделить рабочую поверхность или заготовку на требуемое количество равных частей. Данный метод подходит в первую очередь для больших поверхностей — для труб или кабель каналов уже не сработает.
Как вы поступаете обычно? Замеряете общую длину или ширину, затем делаете вычисления и делите расстояние на нужное количество частей. После чего вновь линейкой или рулеткой отмеряете на поверхности эти части.
После чего вновь линейкой или рулеткой отмеряете на поверхности эти части.
Оказывается все это можно проделать без калькулятора и даже без вычислений. Берете на рулетке число, которое больше чем ширина заготовки, и при этом кратно той величине, на которое вы хотите разделить расстояние.
Например ширина доски 17см, а вам ее нужно разделить на четыре равные части. Сдвигаете рулетку по диагонали до ближайшей отметки в 20см. После чего легко делите эти 20см на 4 и отмечаете метки на расстояниях 5см, 10см, 15см, 20см.
В итоге вы всего одним движением рулетки разделили поверхность на нужное количество частей.
Захотели поделить на 6 частей — ничего сложного. Можно сдвинуть диагональ до 30см и проделать то же самое.
Еще рулеткой на круглой трубе можно точно отмерить поперечный срез. Для этого плотно прижимаете по периметру трубы ленту, совместив концы. Если совместили ровно, никак иначе как под углом в 90 градусов она не ляжет.
Чем шире лента рулетки, тем предпочтительней. Проделать такой же фокус можно и с простым листком бумаги.
Проделать такой же фокус можно и с простым листком бумаги.
Когда невозможно измерить диаметр трубы или заготовки с торца, опять поможет строительная рулетка и геометрия. Обхватываете трубу лентой и измеряете ее окружность. После чего полученный результат нужно разделить на число Пи = 3,14. Это и будет необходимый диаметр.
Еще раз применив знания геометрии, строительной рулеткой без угольников и других инструментов можно проверить точность прямого угла. Как вы знаете из школьного курса — сумма квадратов катетов прямоугольного треугольника равна квадрату гипотенузы.
Берете любую поверхность где должен быть прямой угол, например две стены комнаты. Отмеряете рулеткой в одну сторону 30см, а в другую 40см и ставите метки. Если угол действительно прямой и строители не накосячили, то соединив эти две метки по гипотенузе, вы должны получить на рулетке расстояние ровно в 50см.
Научившись правильно размечать стены будущего дома своими руками, Вы не только сэкономите немного бюджета, но и сможете потом внести какие-то коррективы. Потому что, проект на бумаге – это одно, а когда увидите воочию, как и где в будущем доме будут расположены стены, возможно захотите что-то исправить. А не умея это делать – придется опять платить.
Потому что, проект на бумаге – это одно, а когда увидите воочию, как и где в будущем доме будут расположены стены, возможно захотите что-то исправить. А не умея это делать – придется опять платить.
Сейчас я покажу схематично, один из простых способов разметки как прямоугольных стен любой сложности, так и эркеров, без специальных приспособлений, с помощью одной только рулетки.
Разметка фундамента под дом с прямыми углами
Начнем, пожалуй, с самого простого – разметки дома прямоугольной формы. Тем более что даже дома со сложной планировкой, но с прямыми углами, основываются на этом методе.
Начинается разметка любого по форме дома с определения его местоположения на строительном участке.
Если вы начинаете строить, то у Вас уже должно быть на руках разрешение на строительство и сопутствующие документы, в которых прописан минимальный отступ от всех границ участка.
Начнем с самого простого примера, когда участок, как и дом, имеет прямоугольную форму (см. схему выше). Не имея специальных, дорогостоящих инструментов под рукой, на мой взгляд, самый простой способ произвести разметку фундамента
схему выше). Не имея специальных, дорогостоящих инструментов под рукой, на мой взгляд, самый простой способ произвести разметку фундамента
будет следующий:
- Определяем местоположение будущего дома на участке, в нашем случае это правый нижний угол.
- Выбираем две самые близлежащие границы участка (в нашем случае, это границы, обозначенные на схеме выше — черным цветом).
- Выставляем первые 4 колышка обозначенные цифрами 1-4, в соответствии с отступами от границ участка и натягиваем между ними, как показано черным пунктиром, шнуры. Таким образом, мы нашли один угол нашего дома.
- Затем от колышка №2 замеряем длину, равную длине стены BD, и выставляем колышек №6. Аналогично выставляем колышек №8.
- От колышка №3, вдоль нижней границы участка, отмеряем длину стены CD, и выставляем колышек №7. Аналогично выставляем колышек №5.
- Натягиваем шнуры, как показано на схеме черным пунктиром, получившиеся углы и будут углами дома.
- Проверяем, на сколько правильный получился у нас прямоугольник, методом, описанным ниже.

Стоит отметить, что очень часто бывает так, что участок имеет не прямоугольную форму, тогда необходимо отталкиваться не от двух сторон участка, а только лишь от какой-нибудь одной, натянув лишь один шнур, параллельно ей. Остальные шнуры натягиваются «на глаз», исправляя затем ошибки, как описано далее.
Проверка диагоналей и исправление ошибок разметки фундамента
Если Вы все сделали правильно, то расстояние от точки A до точки D, должно быть равно расстоянию от точки B до точки C. Другими словами – диагонали прямоугольника должны быть равны (менее 1 см – допустимая разница).
Если у Вас обе диагонали равной длины – поздравляю, основная часть разметки пройдена и можно приступать к разметке внутренних стен. Но, к большому сожалению, в большинстве случаев при замерах диагоналей, есть незначительные расхождения. Причин может быть несколько – не совсем прямоугольный участок, высокая трава, мешающая замерам, да и вообще человеческий фактор.
Как быть в этом случае, начинать все заново?
Нет, ни в коем случае! Если расхождения не в метрах, начинать заново ничего не нужно. Надо просто «подправить» углы, сейчас я расскажу, как это сделать.
Надо просто «подправить» углы, сейчас я расскажу, как это сделать.
Допустим, что у Вас диагональ CB получилась длиннее диагонали AD на 20 см, тогда Ваш периметр дома выглядит как на схеме.
Порядок дальнейших действий с разметкой фундамента под дом
:
- Углы A и B сдвигаем влево, примерно на 10 см (половину разницы размеров диагоналей).
- Замеряем заново все стороны и диагонали. Стороны не должны измениться в размерах, но лучше перестраховаться.
- Если разница уменьшилась, но все же они не равны (допустим разница стала 5 см), то повторяем пункты 1 и 2, но уже сдвигая их на 2,5см.
- Если теперь диагональ AD стала больше, то так же повторяем пункты 1 и 2, но сдвигая углы в противоположную сторону (в нашем случае вправо).
Разметка фундамента сложной формы
Хорошо, когда размечается обычный прямоугольный фундамент под дом, сделать это своими руками не представляет никаких трудностей. А как быть, если дом сложной формы.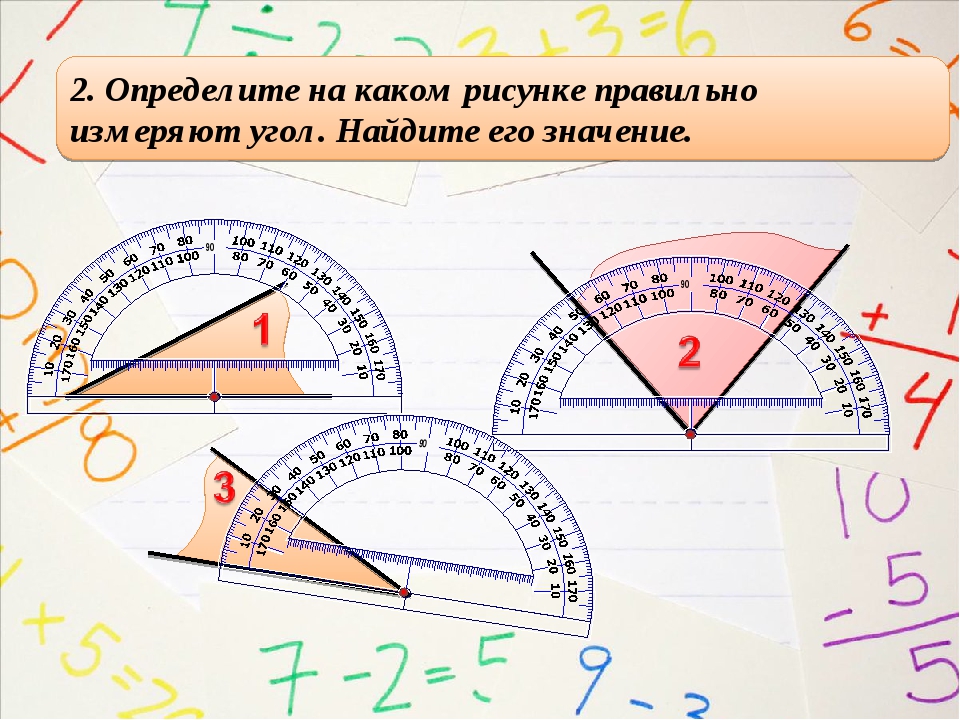
Тут, конечно, разметка будет немного сложнее, но все же не на столько, чтобы за это отдавать часть своего драгоценного бюджета.
Размечая дом сложной формы своими руками, порядок действий должен быть следующий:
- Необходимо дом заключить в прямоугольник, как показано на схеме синим пунктиром (исключив выступающие эркеры).
- Размечаем данный прямоугольник на участке, как в предыдущем разделе, проверяем и поправляем диагонали.
- Затем размечаем все оставшиеся углы таким же способом, как и для прямоугольного дома, только натягивать шнуры будем не от границ участка, а уже от границ самого дома (синего прямоугольника).
- Проверять диагонали каждого отдельного получившегося прямоугольника, в принципе, не надо, потому что если синий прямоугольник получится идеально ровным, то натягивая параллельно его сторонам шнуры, мы получим точную разметку фундамента будущего дома.
Разметка эркера
Сама по себе разметка эркера, хоть и сложнее чем прямоугольная разметка, но тоже не представляет собой особой сложности и опасности, как может показаться на первый взгляд.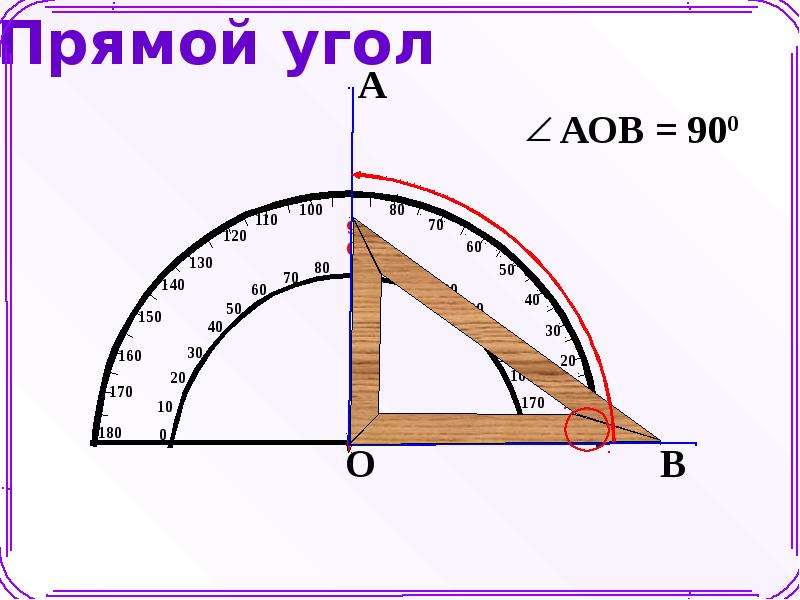
Я не буду так подробно описывать разметку эркера, как это было в предыдущем разделе с фундаментом прямоугольной формы, потому что принципы те же самые. Опишу только нюансы, которые необходимо учесть, если вы делаете это своими руками.
Разметку эркера будем производить так же – своими руками. Порядок разметки фундамента под дом
в виде эркера следующий:
- Итак, дом уже размечен, шнуры не убираем.
- На шнурах 5-7 и 1-3 размечаем выпуклость эркера и натягиваем шнур.
- Затем на нижней границе участка отмеряем длину эркера и выставляем колышек №9.
- Переносим эту длину на сторону дома CD (точка H) и натягиваем шнур между полученной точкой и колышком №9 (уже должны получиться очертания в виде прямоугольника).
- Далее просто от точки C и от точки H, согласно проекту, отмечаем одинаковые расстояния и переносим их на шнур, натянутый в пункте 2 (точки E и F).
Разметка прямых углов фундамента дома с помощью «египетского треугольника»
Есть еще один способ сделать разметку фундамента своими руками – с помощью «египетского треугольника».
Как известно из школьного курса геометрии – «египетский треугольник» это прямоугольный треугольник со сторонами 3, 4 и 5. А в каких единицах, в сантиметрах или километрах – не важно.
Для того, чтобы собрать такой треугольник своими руками, необходимо 3 относительно жестких рейки, размером 3м, 4м и 5м, деревянных или металлических. И если из этих реек собрать треугольник, то он будет прямоугольный.
С помощью такого треугольника можно размечать прямые углы и направления перпендикулярных стен.
Но, как показывает практика, этот треугольник, во-первых, сложно сделать идеальным, а во-вторых, если дом большой, то и треугольник нужен большой, а это просто нецелесообразно. Маленьким треугольником, будет погрешность, которую все равно потом исправлять, измерением диагоналей.
Учитыва вышесказанное — изготавливать «египетский треугольник» своими руками, для разметки фундамента, в большинстве случаев не имеет смысла.
Итак, на первый взгляд, все очень трудно и без профессиональной помощи – не обойтись, но это далеко не так.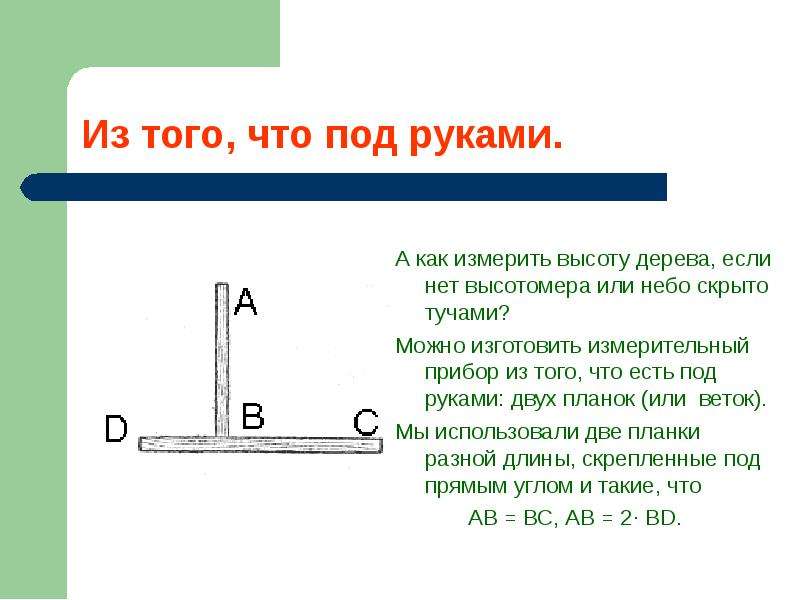 Если вникнуть и понять суть, то разметка фундамента под дом своими руками станет для Вас сущим пустяком.
Если вникнуть и понять суть, то разметка фундамента под дом своими руками станет для Вас сущим пустяком.
Вот несколько советов:
- Перед тем, как начинать разметку, обязательно убедитесь, что Вы сделали достаточные отступы от соседских участков и красной линии (согласно документам).
- Идеальными колышками будут куски арматуры диаметром 10-14мм, так вы сможете более точно произвести разметку фундамента.
- Хорошо натягивайте шнур между колышками, чтобы из-за травы, его направление не отклонялось.
- Натянутые шнуры не убирайте, пока траншея не прокопается лопатой на 2-3 ряда, иначе, точная разметка может превратиться в неровный фундамент.
Внимание! Как бы Вы точно не разметили фундамент под дом
, все равно, при дальнейших работах с ним после заливки, будь то кладка кирпича, блоков или дальнейшая заливка, необходимо перепроверять диагонали.
Многие строители сталкиваются с такой проблемой — как найти угол 90 градусов с помощью строительной рулетки и карандаша?
Давайте рассмотрим как на практике любой желающий в течение нескольких минут может с помощью строительной рулетки и карандаша сделать точный угольник с прямым углом, то есть 90°.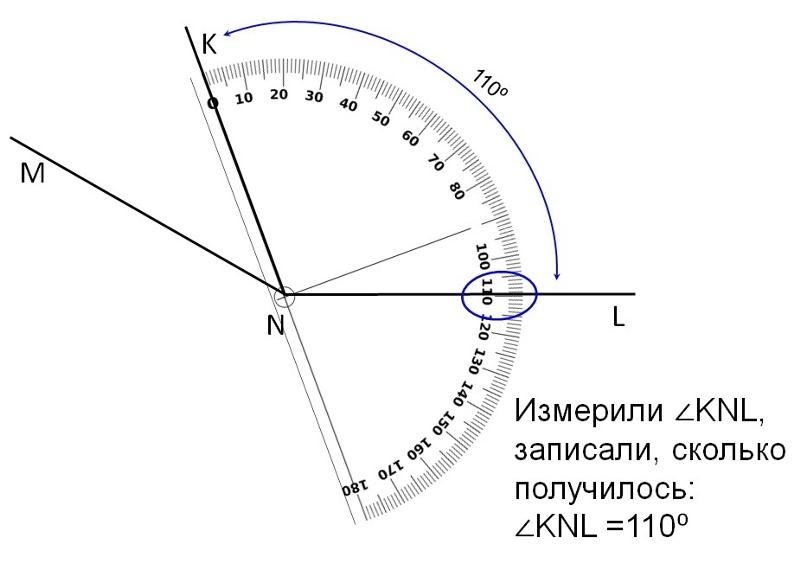
Технология получения треугольника с прямым углом
1. Для начала определимся с системой исчесления, к примеру будем считать в «см».
2. Придумываем любое число, например 20.
Примечание: Здесь может быть любое число на ваше усмотрение. Чем больше число, тем больше размер самого треугольника.
3. Берем комбинацию чисел «3, 4, 5» и последовательно умножаем каждое из этих чисел на придуманное нами число 20.
4. Получаются следующие числа: 60, 80, 100.
5. Присваиваем их поочередно к сторонам треугольника:
- Первый кактет 60 см
- Второй кактет 80 см
- Гипотенуза 100 см.
6. Пользуемся.
Как сделать самому угольник с прямым углом за 5 минут?
1. Соединяем между собой две ровные деревянные рейки, так чтобы одна из них была перпендикулярна другой.
2. Измеряем два катета по выше изложенной системе.
3. Прибиваем деревянную рейку к первой метке.
4. Измеряем гипотенузу и фиксируем на втором катете.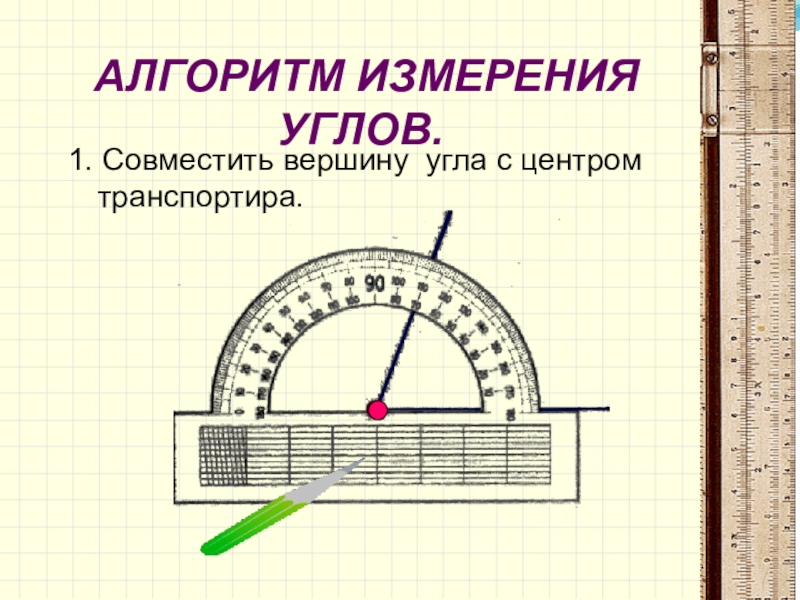
От правильности сделанной разметки будет зависеть долговечность здания. Чтобы сделать разметку не потребуется особых усилий и наличия различных инструментов. Всю работу могут выполнить два человека с минимальным набором инструментов:
- строительный шнур;
- рулетка;
- угольник;
- колышки;
- гидроуровень.
Разметка выполняется после выравнивания стройплощадки. Чем лучше будет подготовлено место, тем легче и удобнее будет переносить проектные схемы с бумаги на саму площадку. Сам процесс можно разделить на разметку внешнего периметра и разметку самого фундамента, включая внутренние перегородки и пристройки к будущему зданию.
Прямоугольный фундамент
Первую сторону фундаментной основы привязывают к какому-либо объекту на площадке. Ориентиром для привязки может служить ограждение участка или соседние постройки. Стоит учитывать и расположение солнца.
Согласно выбранному ориентиру, натягивают первый шнур на нужное расстояние и забивают два колышка.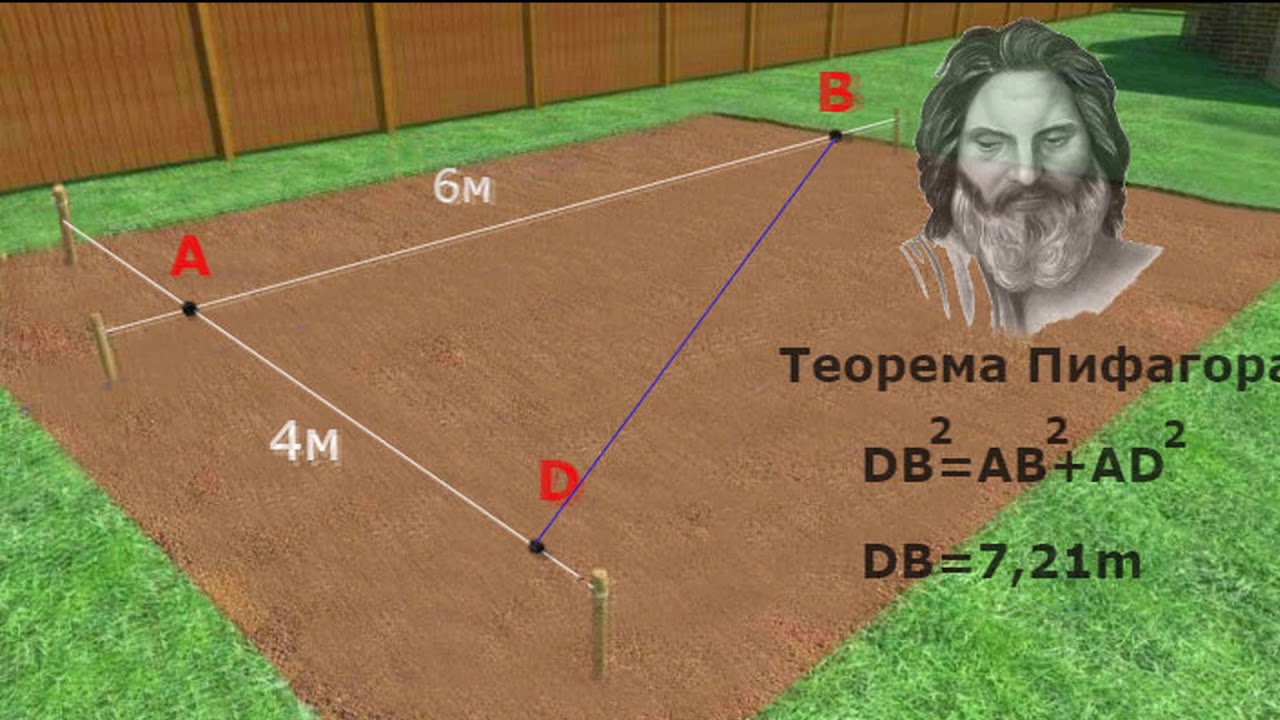 Чтобы колышки не провалились во время копания траншеи, их устанавливают дальше угла фундамента. Места пересечения шнуров будут обозначать углы. Такой способ размещения шнуров позволит сохранить первоначальную разметку при выемке грунта.
Чтобы колышки не провалились во время копания траншеи, их устанавливают дальше угла фундамента. Места пересечения шнуров будут обозначать углы. Такой способ размещения шнуров позволит сохранить первоначальную разметку при выемке грунта.
Разметка внешнего контура и формирование угла фундамента
Например, будет строиться дом 6 х 8. После разметки стороны, которая будет служить его длиной, размечают вторую сторону. Для этого забивают еще колышек, привязывают к нему шнур и натягивают перпендикулярно первому. Точку пересечения шнуров скрепляют. Это и будет угол фундамента. На втором шнуре нужно сделать отметку, которая должна равняться ширине 6 м.
Для формирования угла применяется теорема Пифагора. Чтобы не заниматься глубокими геометрическими расчетами, берут два отрезка 3 м и 4 м. На первом шнуре, который обозначает длину фундамента, от угла отмеряют 4 м и ставят отметку.
На втором шнуре наносят отметку на расстоянии 3 м. Далее рулеткой соединяют одну отметку с другой так, чтобы на рулетке было отделено 5 м.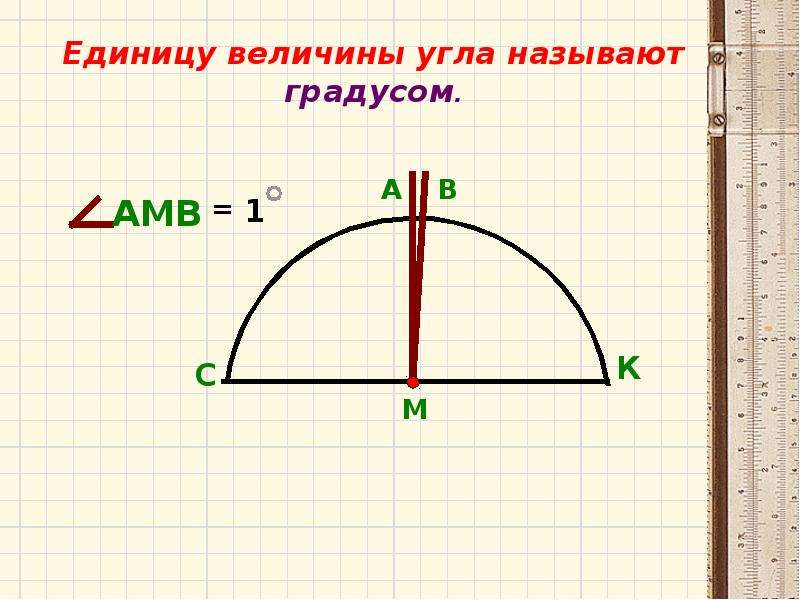 Если расстояние между отметками будет равно 5 м, все нормально. Если нет, то конец второго шнура с отметкой 3 м перемещают, пока рулетка не установится на нужное расстояние.
Если расстояние между отметками будет равно 5 м, все нормально. Если нет, то конец второго шнура с отметкой 3 м перемещают, пока рулетка не установится на нужное расстояние.
Построение прямоугольника
Пошаговая инструкция определения прямого угла
После выравнивания угла в 90 градусов, на шнуре длины делают отметку 8 м, а на шнуре ширины 6 м. Дальше переходят к третьей стороне. Натягивают третий шнур перпендикулярно первому и скрепляют на отметке 8 м.
Четвертый шнур натягивают перпендикулярно второму и скрепляют на отметке 6 м. Чтобы получить четырехугольник с прямыми углами необходимо, чтобы обе отметки на третьем и четвертом шнурах совпали.
Если длины диагоналей четырехугольника одинаковые, то получен прямоугольник. Но диагонали могут быть одинаковые и в равнобедренной трапеции. Поэтому главным условием построения правильного прямоугольника является наличие угла 90º, а в равнобедренной трапеции таких углов нет.
Этот способ является внешней разметкой.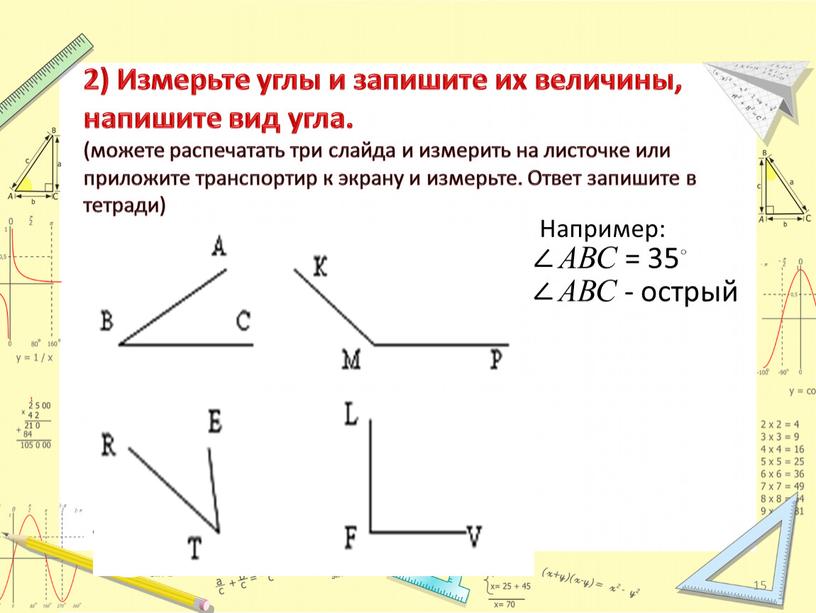 Она подходит для плитного фундамента. При изготовлении фундаментной основы ленточного типа производят разметку по внутреннему периметру, с учетом ширины ленты.
Она подходит для плитного фундамента. При изготовлении фундаментной основы ленточного типа производят разметку по внутреннему периметру, с учетом ширины ленты.
После того, как первоначальная разбивка сделана, переходят ко второму этапу — обноски территории. Это позволит сохранить натянутые шнуры, обозначающие контуры основы до конца строительства.
Обноски устанавливают за пределами траншей. Они состоят из попарно вбитых столбиков, соединенных планкой. Установка обноски является ответственным моментом. Их монтируют так, чтобы верхние части планок были на одном уровне. Для этого и требуется гидроуровень. Шнуры, натянутые на верхние планки, будут служить нулевой горизонтальной отметкой опоры.
Разметка под плитный фундамент
Эта работа легкая, но является важным этапом строительства. Без точной разбивки, дальнейшая эксплуатация будущего дома может обернуться частым ремонтом здания и фундаментной основы.
Как произвести правильно эту работу? Для этого на подготовленном участке с помощью колышков и шнуров наносят наружный контур основания. Потом через обноски натягивают шнуры, которые будут служить нулевой отметкой и черновым полом будущего дома. Особенностями разметки плитного фундамента является:
Потом через обноски натягивают шнуры, которые будут служить нулевой отметкой и черновым полом будущего дома. Особенностями разметки плитного фундамента является:
- проводить ее проще, потому что здесь достаточно разметить только внешний контур периметр, а с установкой внутренних стен и перегородок определяются уже, когда фундамент готов;
- разбивку опоры делают на 1 м шире во все стороны от периметра, чтоб была возможность установить дренажную систему и отмостку;
- если в проекте предусмотрена терраса, балкон или другие пристройки, их тоже размечают и заливают вместе с фундаментом.
Ведь это основание должно быть монолитным и гарантировать целостность и надежность построенного объекта.
Ленточное основание и столбчатый фундамент
Делается разбивка внешнего контура по теореме Пифагора. Дальше отступают проектную ширину ленты и выполняют разметку внутри. Шнуры закрепляют за установленные обноски на высоте нулевой горизонтальной отметки.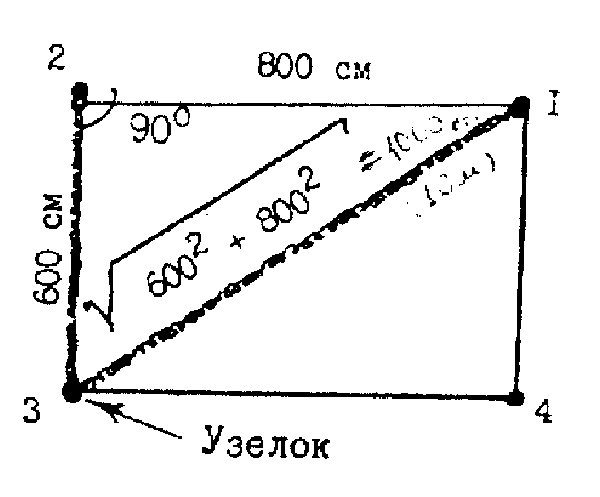
Со столбчатым фундаментом вся работа выполняется так же, как под ленточное основание. Отличие в том, что по углам и по всему периметру, согласно проектной документации, наносят разметку на места заглубления столбов.
После заглубления столбов до проектной отметки и при наличии в проекте установки ростверка, делают еще одну разметку, применив двухъярусную обноску.
Сначала натягивают шнуры для внешнего и внутреннего периметров ростверка на уровне оголовок столбов. Дальше выполняют верхнюю обноску на уровне ростверка.
Если фундамент произвольной конфигурации
Очень часто фундаменты имеют неправильную форму. Современные постройки могут иметь Г- или Т-образную форму, разные выступы. Отдельные стены здания бывают округленными.
Но даже при очень сложном фундаменте начинают с разметки прямоугольника, а уже к нему добавляют другие фигуры.
Для крыльца или дымохода камина выполняют прямоугольное основание. Их можно просто пристроить к основному фундаменту без установки дополнительных шнуров. Но в некоторых случаях устанавливают дополнительные обноски.
Но в некоторых случаях устанавливают дополнительные обноски.
Разметку окружностей, дуг и многоугольных элементов выполняют относительно их центра. Для круглой основы вбивают колышек в нужную точку фундамента, и с помощью шнура вместо циркуля наносят линии основания.
При разметке многоугольного элемента размечают квадрат, а потом формируют многоугольник. Возле каждого угла ставят обноски, и шнуром намечают периметры.
Неправильная форма опоры
Такие основания встречаются редко, но если возникла такая потребность, то разметку делаем так: на чертеж накладывают кальку с координатной сеткой и намечают опорные точки.
Потом натягивают координатную сетку из шнуров и на следующем этапе, с помощью этой сетки, переносят все опорные точки контура на грунт.
Подводя итог, можно сказать, что разметка фундамента своими руками не представляет трудности и не требует определенного опыта. Сделать его может любой застройщик на своем участке самостоятельно, без применения каких-либо сложных инструментов.
Единственной трудностью может послужить нанесение разметки нулевой горизонтальной точки. Для этого используют гидроуровень или нивелир. Но и в этом случае можно применить простой дедовский способ.
Понадобится обычный длинный поливной шланг. Если он изготовлен из непрозрачного материала, то на его концы добавляют отрезки из прозрачной трубки и заливают в него воду. Один конец шланги подводят к выбранной нулевой точке и совмещают уровень воды с этой точкой. Уровень воды на втором конце шланги и будет означать нулевой горизонтальный уровень.
Разметка под фундамент своими руками
В данной статье опишем процесс разметки участка под фундамент своими руками.
План статьи:
Общие правила для разметки фундамента
Построение прямоугольного фундамента (т.Пифагора)
Построение прямоугольного фундамента (метод паутина)
Разметка под столбчатый фундамент
Разметка под ленточный фундамент
Разметка под плитный фундамент
Общие правила для любого фундамента
Выбираем точку отсчета. Первую сторону нашего фундамента нужно привязать к какому-нибудь объекту нашего участка.
Первую сторону нашего фундамента нужно привязать к какому-нибудь объекту нашего участка.
Пример. Сделаем так, чтобы наш фундамент (дом) был параллелен одной из сторон забора. Следовательно, первую бечевку натягиваем равноудалено от этой стороны забора на нужное нам расстояние.
Построение прямого угла (90⁰). В качестве примера будем рассматривать прямоугольный фундамент, в котором все углы максимально близки к 90⁰.
Существует несколько способов как это сделать. Мы рассмотрим 2 основных. © www.gvozdem.ru
Способ 1. Правило золотого треугольника
Для построения прямого угла будем применять теорему Пифагора.
Формула
Чтобы не углубляться в геометрию попробуем описать проще. Чтобы между двумя отрезками a и b сделать угол в 90⁰ нужно сложить длины этих отрезков и вывести корень из этой суммы. Получившиеся число будет являться длинной нашей диагонали соединяющей наши отрезки. Очень просто расчет сделать с помощью калькулятора.
Очень просто расчет сделать с помощью калькулятора.
Обычно при разметке фундамента берут размеры сторон, чтобы при выведении из корня получалось целое число. Пример: 3х4х5; 6х8х10.
Если у вас есть рулетка, то в целом проблем не возникнет, если вы будете брать отрезки отличные от общеиспользуемых. Например: 3х3х4,24; 2х2х2,83; 4х6х7,21
Если измерения мы производили в метрах, то значения получаются очень даже понятными: 4м24см; 2м83см; 7м21см.
Калькулятор
Также стоит отметить, что измерения можно производить в любых системах измерения длины главное использовать известное нам соотношение сторон: 3х4х5 метра, 3х4х5 сантиметра и т.п. То есть, если даже у вас нет инструмента для измерения длины, то можно взять, например, рейку (длина рейки не имеет значения) и померить ей (3 рейки х 4 рейки х 5 реек).
Теперь давайте посмотрим как это применить на практике.
Инструкция по разметке прямоугольного фундамента
Способ 1.
 Правила золотого треугольника (т.Пифагора)
Правила золотого треугольника (т.Пифагора)
Рассмотрим на примере построение прямоугольного фундамента с размерами 6х8м с помощью золотого треугольника (т.Пифагора).
1. Размечаем первую сторону фундамента. Это самая простая часть в построении нашего прямоугольника. Главное, что нужно помнить. Если хотим чтобы наш фундамент (дом) был параллелен одной из сторон забора либо другого объекта на участке или за его пределами, то первую линию нашего фундамента делаем равноудаленной от выбранного нами объекта. Данную процедуру мы описывали выше. Для размещения первой бечевки можно использовать колушки, прочно закрепленные в грунте, но в идеальном варианте для данной цели использовать обноску. Ее и будем использовать. Расстояние между обносками для данной стороны сделаем 14м: между обносками и будущими углами по 3м и 8м под фундамент.
2. Натягиваем вторую бечевку максимально перпендикулярно первой. Идеально перпендикулярно на практике натянуть сложно, поэтому на рисунке мы также отобразили ее не много отклоненной.
3. Скрепляем обе бечевки в точке пересечения. Скрепить можно скобкой либо скотчем. Главное чтобы надежно.
4. Приступаем к формированию прямого угла с применением теоремы Пифагора. Будем строить прямоугольный треугольник с катетами 3 на 4 метра и гипотенузой 5 метров. Для начала отмеряем на первой бечевке 4 метра от места пересечения бечевок, а на второй 3 метра. Ставим отметки на шнурке с помощью скотча (прищепка и т.п.).
5. Соединяем рулеткой обе отметки. Один конец рулетки фиксируем у отметки в 4 метра и ведем в сторону отметки в 3 метра на другой бечевке.
6. Если у нас прямоугольный треугольник, то обе отметки должны сойтись при расстоянии в 5 метров. В нашем случае отметки не сошлись. Поэтому перемещаем бечевку в нашем случае вправо до того момента когда отметка на 3 м совпадет с делением рулетки на 5 м.
7. В итоге у нас получился прямоугольный треугольник с углом в 90⁰ между двумя бечевками.
8. Больше отметки нам не нужны и их можно убрать.
9. Приступаем к построению прямоугольника. Отмеряем на обеих бечевках длины сторон нашего фундамента 6 и 8 метров соответственно. Ставим отметки на бечевках.
10. Натягиваем третью бечевку максимально перпендикулярно к первой бечевке. Скрепляем обе бечевки на отметке в 8 м.
11. Натягиваем четвертую бечевку максимально перпендикулярно ко второй бечевке. Скрепляем обе бечевки на отметки в 6 метров.
12. Делаем отметки на третьей бечевке 6 метров и на четвертой 8 метров.
13. Чтобы получить четырехугольник с прямыми углами в нашем случае необходимо, чтобы обе отметки на третьей и четвертой бечевках совпали. Для этого перемещаем обе бечевки до момента соединения отметок.
14. В итоге, если все правильно измерили, то у нас должен получиться правильный прямоугольник. Давайте проверим, получился ли он с помощью измерения диагоналей.
15. Измеряем длины диагоналей. Если они одинаковые, как в нашем случае, мы имеем правильный прямоугольник. Диагонали имеют одинаковую длину и в равнобедренной трапеции. Но у нас известен один угол в 90⁰, а в равнобедренной трапеции таких углов нет.
16. Готовая разметка прямоугольного фундамента с применением теоремы Пифагора. © www.gvozdem.ru
Способ 2. Паутина
Очень простой способ сделать разметку в виде прямоугольника с углами в 90⁰. Самое главное что нам понадобится — это бечевка, которая не растягивается, и точность ваших измерений с помощью рулетки.
1. Нарезаем куски бечевки, которые нам понадобятся для формирования разметки. В данном примере мы строим фундамент со сторонами 6 на 8 метров. Также для правильного построения прямоугольника нам понадобятся равные диагонали, которые для прямоугольника 6 на 8 метров будут равны 10 метрам (т.Пифагора описана выше). Также нужно взять запас длины бечевок на крепление.
2. Соединяем нашу «паутину» как на рисунке. Скрепляем стороны с диагоналями в 4 местах по углам. Сами диагонали в точке пересечения скреплять не нужно.
3. Натягиваем первую бечевку (точки 1,2). Крепить ее будем с помощью колышков. Главное чтобы колышки крепко держались в земле и при натяжении нашей конструкции их не увело. Этот важный момент нужно учесть.
4. Натягиваем угол 3. Главное условие чтобы бечевка 1-3 и диагональ 2-3 не провисали и были максимально натянуты. После фиксации с помощь колышка в точке 3 мы имеем угол в точке 1 в 90⁰.
5. Натягиваем угол 4 и устанавливаем колышек. Следим, чтобы бечевка в точках 2-4, 3-4 и диагональ 1-4 не провисали и были максимально натянуты.
6. Если соблюдены все условия, то в результате у нас должен получиться прямоугольник с углами максимально близкими 90⁰.
Разметка под фундамент дома
Разметка под столбчатый фундамент
Делаем двухъярусную обноску. Нижний ярус – это уровень столбов.
Верхний ярус обноски – уровень ростверка.
Подробную инструкцию читаем в статье: Разметка под столбчатый фундамент с ростверком
Разметка под ленточный фундамент
Создаем прямоугольник для внешнего контура применяя т.Пифагора. Затем отступаем на величину, равную ширине ленты и делаем внутренний контур.
Разметка под плитный фундамент
Самой простой способ разметки. Строим прямоугольник по размерам фундамента применяя теорему Пифагора для нахождения прямого угла. © www.gvozdem.ru
От автора
В данной статье мы рассмотрели, как произвести разметку под фундамент своими руками с построением прямоугольника с углами в 90⁰. В целом ничего сложно в разметке нет. Цена вопроса – это стоимость бечевки, доски для обноски (эконом вариант — колышки) и умение пользоваться рулеткой.
Похожие статьи:
Самый простой способ как можно вычислить прямой угол подручными средствами
Каждый из нас учился в школе. Там человек получает огромное количество тех знаний, которые впоследствии могут понадобиться в жизни. Не все, конечно, могут в полной мере оценить значимость полученных знаний в школьной время, но сейчас речь не об этом.
Математика. Это страшное для многих слово, которое пугало достаточное количество школьников в своё время. Цифры, формулы и расчёты поддавались только самым пытливым. И с каждым годом этот сложный предмет становился всё сложнее и сложнее.
В старших классах появляется геометрия и всё становится ещё сложнее и непонятнее. Возможно, многие хоть раз в жизни, но в сердцах проклинали непонятную им науку и задавались вопросом, зачем это вообще нужно, и понадобится ли это в жизни.
Возможно, в повседневной жизни применить полученные в школе знания не удавалось. Вряд ли требовалось посреди белого дня высчитывать логарифмы и квадратные уравнения или доказывать, что две параллельные никогда не сойдутся. Но, где уж точно могут понадобиться знания геометрии и математике, так это в строительстве и при осуществлении ремонта.
В данной статье речь пойдёт о вычислении прямого угла, что требуется при строительстве зданий. Точность при возведении строений должна быть соблюдена в обязательном порядке, ведь только точные расчёты могут избавить от перекосов и нестабильности организации всего здания. Вычисление прямого угла при строительстве — не такой уж и трудный процесс, при котором потребуется знание и применение некоторых простых правил математики и геометрии. Подробнее об этом будет рассказано ниже.
Действительно ли прямой угол?
Возможно, некоторые читатели, ознакомившиеся с заголовком данной статьи, возразят, что прямой угол можно получить не всегда, и не всегда при строительстве используются именно ровные и точные прямые углы.
И, в принципе, они правы. Получить его весьма сложно, особенно если наблюдается неровность фундамента, на котором осуществляется строительство здания. Но, даже учитывая это обстоятельство, ни в коем случае нельзя делать вывод, что расчёт прямого угла можно делать просто «на глаз». В любом случае, если не представляется возможным вычислить идеальный прямой угол, то требуется достичь наиболее приближённого значения к идеальному углу в 90 градусов. И этого можно добиться, используя незатейливые инструменты и не самые сложные математические знания и познания в геометрии.
Что понадобится для определения прямого угла?
Итак, какие инструменты понадобится использовать для того, чтобы проверить прямой угол. Сразу стоит отметить, что никаких приборов и серьёзных инструментов для этого не потребуется. Нужно будет использовать весьма простые вещи, которые могут найтись практически в каждом хозяйстве. И даже если их не имеется под рукой, их с лёгкостью можно приобрести в магазине. С этим никаких трудностей не возникнет.
Для вычисления прямого угла нужно взять:
- Карандаш;
- Строительную рулетку.
И всё. Вот так вот всё просто.
Как можно вычислить прямой угол?
Итак, в этой статье будет описан принцип 3-4-5 при определении угла в 90 градусов. Ничего сложного в этом нет. Потребуется просто лишь чуть пораскинуть мозгами и вникнуть во все расчёты, которые смогут помочь в проверке угла.
Итак, нужно обозначить следующие шаги:
- Для начала стоит разобраться в том, почему принцип так обозначен — 3-4-5. Это не просто набор цифр, это величина сторон прямоугольного треугольника. Теорема Пифагора гласит: квадрат гипотенузы равен сумме квадратов катетов. Цифры 3-4-5 очень подходят для проверки этого простого правила геометрии: 3*3+4*4=5*5, то есть 9+16=25. Именно эти цифры и будут использоваться в дальнейших вычислениях;
- Итак, потребуется для начала отмерить 3 метра от угла вдоль одной из стен. Тут следует отметить, что 3 метра — предпочтительная длина замера, но в том случае, если комната маленькая, можно отметить всего 30 сантиметров. В месте замера нужно сделать отметку;
- В принципе, можно использовать и другие цифры, но рекомендуется в любом случае использовать пропорционально увеличенные числа, например: 9-12-15 или же 30-40-50;
- После проделанного предварительного замера нужно отмерить 4 метра вдоль другой стены, тоже от угла. Ну или соответственно 40 сантиметров, если комната маленькая. Нужно сделать отметку;
- Теперь остаётся сделать последнее действие, по которому уже можно судить прямой угол или нет. От измеряющего потребуется измерить расстояние между сделанными отметками. По полученным данным можно будет сделать определённые выводы:
- Если расстояние между отметками будет равняться 5 метрам ровно, это будет означать, что угол является прямым;
- В том случае, если измеренное расстояние будет равняться меньше 5 метров, угол будет меньше, чем 90 градусов;
- Ну и, наконец, величина угла будет составлять больше 90 градусов, если полученная величина замера будет равняться больше 5 метров.
Вывод
Вот, как просто можно вычислить прямой угол без использования каких-либо строительных инструментов и приборов. Использовать можно самое простое, но в то же время весьма действенное средство, которое вкупе с использованием имеющихся знаний и бесхитростных расчётов, может помочь произвести измерение.
При использовании предложенных величин, ключевым становится финальный замер между двумя отметками, которые были сделаны ранее. Расстояние, которое будет равняться точно 5 метрам, покажется, что он прямой. Если же величина будет больше или меньше 5 метров, это будет означать, что он прямым не является.
Как расположить под прямым углом в строительстве
Выложить точные прямые углы на строительных проектах, таких как фундаменты под навесы, настилы или террасы , легко, если вы используете геометрию.
Согласно теореме Пифагора, квадрат двух сторон треугольника, примыкающих к прямому углу (катеты), равен квадрату третьей стороны (гипотенузы). Математически это выражается как a² + b² = c².
Для использования умножьте длину каждого катета треугольника на себя, затем сложите две суммы вместе, чтобы найти длину гипотенузы, когда угол равен 90 °.
Самый простой способ сделать это — использовать метод 3-4-5:
- Отмерьте 3 фута от угла, который вы хотите сделать 90 ° в одном направлении.
- Отмерьте 4 фута от угла, который вы хотите сделать 90 ° в другом направлении.
- Измерьте поперек двух точек и отрегулируйте угол так, чтобы расстояние на третьей стороне треугольника составляло 5 футов.
Вы также можете использовать числа, кратные 3-4-5, в том же соотношении (например, 6, 8, 10) для образования больших или меньших прямых углов.
Посмотрите это видео, чтобы узнать больше.
Дополнительная литература
ВИДЕО ТРАНСКРИПТ
Джо Труини: Вы, возможно, не думали, что когда-нибудь дойдете до использования геометрии средней школы, но если вам когда-либо приходилось выкладывать линии идеально квадратными, под углом 90 градусов угол, вот шанс его использовать.
Если это такой большой проект, как этот, где мы расширяем внутренний дворик, квадрат обрамления был бы слишком маленьким; это было бы недостаточно точно. Итак, мы собираемся использовать теорему Пифагора, основанную на соотношении три, четыре, пять.
Итак, вдоль одной линии я измерил и отметил три фута, а вдоль пересекающейся линии я проделал то же самое, только на четырех футах. А теперь, чтобы применить теорему на практике, вы просто измеряете поперек двух линий и перемещаете кол, внутрь или наружу, пока пятиметровая отметка не совпадет с отметкой, сделанной вами на этой линии. Потом можно вбивать ставку.
И он не будет идеально выровнен в первый раз, но вы можете перемещать ставку внутрь или наружу, из стороны в сторону, как вам нужно.
И это работает — здесь я сделал это на трех, четырех и пяти футах. Но вы можете использовать любое из этих соотношений, например, шесть, восемь или 10. Чем крупнее проект, тем больше числа, тем точнее он будет.
Получение квадрата с треугольником 3: 4: 5
Этот пост может быть немного математическим ботаником, но иногда в строительстве математический ботаник — это тот, кто делает разницу между падением здания и тем, которое длится сто лет. Старые дома заброшены…]
Читать далее
Пост «Получение квадрата с треугольником 3: 4: 5» первым появился в блоге Craftsman.
Известно, что в старых домах отсутствуют прямые углы. Они менялись и оседали с годами, и все не ровно и не ровно. Но я научу вас, как это исправить.
Признаюсь, математика не была моим лучшим предметом в школе. Я гораздо более наглядный человек, и страница, полная цифр, никак не влияет на мое художественное чутье. Но был один курс математики, который имел для меня некоторый смысл.Геометрия. При строительстве и реконструкции геометрия может быть вашим лучшим другом. (Прошу прощения, если это начинает звучать как особенное после школы.)
Вы помните теорему Пифагора?
? Я тоже. Но треугольник 3: 4: 5 для непрофессионала заменяет теорему Пифагора. Треугольник 3: 4: 5 — лучший из известных мне способов определить с абсолютной уверенностью, что угол составляет 90 градусов. Это правило гласит, что если одна сторона треугольника имеет размер 3, а соседняя сторона — 4, то диагональ между этими двумя точками должна иметь размер 5, чтобы он был прямоугольным.Еще не запутались?
Это может быть 3 мм, 3 дюйма, 3 фута или 3 мили. Неважно, какую единицу измерения вы используете, пока вы придерживаетесь соотношения 3: 4: 5. И вы также можете использовать кратные 3: 4: 5, например 6: 8: 10 или 9:12:15. Используйте то, что хотите, хотя 3: 4: 5 легче всего запомнить.
Строите колоду, обрамляете стену, кладете плитку? Почти каждый строительный объект в какой-то момент требует прямых углов. А с треугольником 3: 4: 5 вы можете найти свои прямые углы без каких-либо сложных вычислений.
Выберите одну ногу вашего проекта и отмерьте 3 фута от угла. Отметьте на доске отметку в 3 фута. Теперь измерьте соседнюю доску от того же угла до 4 футов и поставьте там отметку. Затем измерьте расстояние между двумя отметками. Если это 5 футов, то у вас идеально квадратный угол. Поздравляю! Если размер меньше 5 футов, угол слишком мал (<90 градусов) и его необходимо немного увеличить. Если он больше 5 футов, угол слишком большой (> 90 градусов) и его необходимо немного закрыть.
Этот удобный трюк убережет вас от серьезных ошибок в будущем. Я знаю, что это самый полезный математический элемент, кроме 1 + 1 = 2, и я использую его почти каждую неделю. Надеюсь, теперь вам не придется гадать, правильны ли ваши проекты. Используя треугольник 3: 4: 5, вы можете знать наверняка.
Какие еще полезные математические приемы вы используете в строительстве, о которых мы могли не знать?
Рулетка | |
| |
Комбинированный квадрат | |
| |
Карпентерская площадь (также называемая Рамочной площадью) | |
| |
Длинная прямая кромка | |
| |
уровень | |
| |
Метрология — что измерять
Сначала это может показаться «легкой задачей», но решить, что измерять, может быть непросто.Первая часть этой задачи — определить, какие измерения необходимы, чтобы установить соответствие определенным критериям. Далее необходимо определить, доступны ли инструменты, необходимые для выполнения требуемых измерений, и, если нет, то как обеспечить выполнение требований с помощью имеющихся инструментов.
Скажем, например, что нам нужно определить размер металлической пластины, а также определить, является ли она квадратом. В нашем распоряжении есть возможность измерять длину с помощью рулетки, но нет возможности измерять углы.Мы знаем, что квадрат — это форма, у которой четыре равные стороны, которые являются прямыми линиями. Кроме того, чтобы быть квадратом, эта форма должна иметь прямые углы в углах. Измерение четырех сторон нашей металлической пластины и обнаружение их одинаковой длины не позволяет нам сделать вывод, что форма является квадратом, потому что углы могут быть не прямыми.
По определению квадрат имеет четыре стороны равной длины, расположенные под углами 90 градусов. Оба критерия должны быть выполнены, чтобы объект был квадратом.Прямоугольник будет иметь четыре стороны с углами 90 градусов, но не будет квадратом, потому что не все стороны будут одинаковой длины.
Вместо этого форма может быть параллелограммом, который соответствует этому критерию для всех сторон, равных, но не удовлетворяет второму требованию о том, что углы являются прямыми (или 90 градусов) углами. Теперь, поскольку у нас есть возможность измерять длину, но нет возможности измерять углы, мы не можем, исходя из того, что все стороны имеют одинаковую длину, быть уверенными в том, что металлическая пластина является квадратом, не зная углов на углах.Однако проявив немного изобретательности (и еще меньше математики), мы можем определить, является ли тарелка квадратом. Мы знаем, что если объект представляет собой квадрат, его диагонали также должны быть одинаковой длины. Мы могли бы использовать немного более сложную математику и выяснить, какой должна быть длина диагонали треугольника с двумя равными сторонами определенной длины для угла их пересечения на угол 90 градусов. Но есть еще более простое решение. Диагонали должны быть одинаковой длины! Итак, измерив четыре стороны и определив, что все они имеют одинаковую длину, а затем диагонали, чтобы убедиться, что они имеют одинаковую длину, можно удовлетворить наши потребности, используя только измерения длины.
В некоторых случаях альтернативные средства, описанные выше, могут дать более точные измерения, чем те, которые можно было бы сразу считать интуитивно понятными или «традиционными». Например, при съемке земли легко измерить длину с большей точностью, чем углы. Допустим, геодезист хочет разметить участок земли со стороной 100 футов и ровно квадратным. Начиная с угла, геодезист с помощью рулетки устанавливает точку точно в 100 футах.Геодезист смотрит на эту точку из начальной точки, используя транзит (ту штуку, похожую на телескоп, которую используют геодезисты). Затем геодезист поворачивает проход на 90 градусов (телескоп откалиброван), чтобы установить линию, вдоль которой будет измеряться вторая сторона длиной 100 футов. Транзит — это очень точный инструмент, способный измерять углы с разумной точностью, но, к сожалению, очень небольшая неточность в измерении угла приведет к значительно большей неточности по мере увеличения расстояния от устройства.Поскольку измерения расстояния обычно более точны, чем измерения углов, измерение длин диагоналей в этом случае, вероятно, приведет к созданию более точного участка земли.
Интересный боковой фон — Мой сосед недавно закладывал фундамент из цементных блоков для сарая, которое он купил. Он знал размеры сарая, но также должен был убедиться, что фундамент, который он собирался построить, имел квадратные углы.Как инженер я видел в этом реальную проблему. У меня есть строительный квадрат, но, конечно, он не может точно установить надежный квадратный угол, так как его самая длинная рука имеет длину всего около 2 футов, а сарай — 10 футов на 12 футов. Однако у соседа было интересное и простое решение, которое он назвал правилом 3, 4, 5. Треугольник со сторонами, длина которых составляет 3 единицы, 4 единицы и 5 единиц, определяет прямой угол на пересечении длинных сторон 3 и 4 единицы. Это был простой способ определить его квадратные углы, которые, будучи инженером, я должен был проверить, используя мое правило равной диагонали, как описано выше.Удобно то, что единицы измерения могут быть любыми — дюймы, футы, метры, ярды, мили. . .
Во многих случаях «очевидные» измерения приводят к результатам, которые либо менее точны, чем возможно, либо просто бессмысленны. Определение того, какие параметры использовать для достижения требуемой точности, имеет решающее значение для успешной метрологии.
— FJF —
Измерение углов и расстояний до точной модели
Что отличает прочную конструкцию и дизайн от M.Оптическая иллюзия К. Эшера? Точные измерения.
В SketchUp инструменты «Рулетка», «Транспортир» и поле «Измерения» позволяют точно моделировать:
Помимо этих инструментов, вы также можете объединить советы из этой статьи с небольшой математикой, чтобы точно оценить высоту здания.
Измерение расстояния
Инструмент «Рулетка» может измерять расстояние, создавать направляющие или отображать координаты по оси x. Вот где вы найдете рулетку в интерфейсе SketchUp:
- Панель инструментов «Начало работы»
- Строительный инструмент
- Панель инструментов большого набора инструментов
- Меню инструментов в строке меню
- Палитра инструментов (macOS)
Совет: Выбрав инструмент «Рулетка», вы можете сразу увидеть длину линии или площадь лица.Наведите курсор рулетки на линию или грань, и вы увидите расстояние или площадь в поле «Измерения».
Чтобы измерить геометрию или установить направляющую линию, выполните следующие действия:
Примечание: Хорошее правило, которое следует запомнить; Вы будете использовать конечные точки для создания направляющих , точек , вы можете создать направляющие , линии , используя средние точки, линии или грани.
- Выберите инструмент Рулетка () или нажмите кнопку T .
Примечание. По умолчанию инструмент «Рулетка» настроен на создание направляющих линий и направляющих точек во время измерения.В режиме создания направляющих рядом с курсором рулетки появляется знак плюса (). Если вы хотите просто измерить между двумя точками без создания направляющей, вы можете нажать Ctrl (Microsoft Windows) или Option (macOS). В этом режиме значок «плюс» рядом с инструментом «Измерить» исчезает. Этот режим будет действовать до тех пор, пока вы не переключите инструменты. - Щелкните начальную точку измерения. Если вам нужно выбрать конечную или среднюю точку, механизм вывода SketchUp поможет вам найти ее. Чтобы создать направляющую линию, щелкните линию, которая должна быть параллельна вашей направляющей линии.
- Переместите курсор в направлении, которое вы хотите измерить. Когда вы перемещаете мышь, временная линия измерительной ленты со стрелками на каждом конце тянется от вашей начальной точки, как показано на рисунке.
Совет: Вот несколько советов, которые помогут вам перемещать курсор рулетки в трехмерном пространстве:
- Линия измерительной ленты меняет цвет в соответствии с цветами оси, когда она параллельна любой оси. На рисунке вы видите измерительную ленту, выровненную по красной оси.
- Нажмите и удерживайте кнопку направления во время измерения, чтобы заблокировать ось.Стрелка вверх блокирует синюю ось, стрелка влево блокирует зеленую ось, а стрелка вправо блокирует красную ось.
- В поле «Измерения» динамически отображается длина вашей измерительной ленты.
- Нажмите Esc , если вам нужно начать все сначала.
- (необязательно) Чтобы создать направляющую линию, нажмите Ctrl (Microsoft Windows) или Option (macOS). Рядом с курсором рулетки () появится знак плюса.
- Щелкните в конечной точке измерения. Расстояние от начальной точки отображается в поле «Измерения». Если вы нажали Ctrl на предыдущем шаге, направляющая линия появится в виде пунктирной линии, которая проникает в бесконечное трехмерное пространство (по крайней мере, в вашей модели). На следующем рисунке указатели отмечают расстояние 3 фута от внутренних стен. (См. Раздел Добавление текста в модель для получения информации о маркировке расстояний в вашей модели.)
- (Необязательно) Чтобы переместить направляющую линию на точное расстояние от начальной точки, введите число и единицу измерения, а затем нажмите . Введите .
Совет: При измерении от конечной точки и создании направляющей SketchUp создает направляющую точку, как показано на рисунке. Направляющая точка — это конечная пунктирная линия, а направляющая линия — бесконечная.
Измерение угла
Измерьте угол, если вы хотите продублировать этот угол в другом месте модели или создать планы, например, для проекта деревообработки. Чтобы измерить угол или создать наклонные направляющие линии, используйте инструмент Транспортир.
Инструмент Транспортир () находится в нескольких частях интерфейса SketchUp:
- Строительный инструмент
- Панель инструментов большого набора инструментов
- Меню инструментов
- Палитра инструментов (macOS)
На видео вы увидите, как измерять углы и устанавливать направляющие с помощью инструмента Транспортир. Чтобы узнать, как пройти через этот процесс, прочтите оставшуюся часть этого раздела.
Чтобы измерить угол и создать наклонную направляющую линию, выполните следующие действия:
- Выберите инструмент Транспортир ().Курсор изменится на транспортир. Центральная точка зафиксирована на курсоре.
- Щелкните, чтобы задать вершину угла, который нужно измерить. (См. Выноску 1 на рисунке.) Если вам нужно заблокировать ориентацию, нажмите и удерживайте клавишу Shift перед тем, как щелкнуть.
Совет: Когда вы нажимаете и удерживаете клавишу Shift, чтобы заблокировать / ограничить плоскость вращения, вы можете нажать Alt (Microsoft Windows> или Command (macOS), чтобы освободить транспортир от предполагаемой плоскости. Угол транспортира будет остается углом исходной плоскости, но теперь вы можете перемещать транспортир, чтобы вывести другую геометрию.
- Щелкните в том месте, где начинается угол, который вы хотите измерить. (См. Выноску 2 на рисунке.)
Совет: Вы можете щелкнуть и перетащить от вершины к первой точке, чтобы определить ось вращения. Это особенно полезно, если вам нужно вращать по оси, которая не находится в красной, зеленой или синей плоскостях. Нажмите Esc в любой момент, чтобы начать все заново.
- Переместите курсор, чтобы измерить угол. (См. Выноску 3 на рисунке.)
Совет: Вот несколько советов, которые помогут вам найти измерение прямого угла:- При перемещении курсора угол динамически отображается в поле «Измерения».
- Когда курсор находится близко к транспортиру, угол привязывается к делениям транспортира, которые показывают приращение 15 градусов. Когда ваш курсор находится дальше от центра транспортира, вы можете измерить угол более точными измерениями.
- Щелкните, чтобы установить наклонную направляющую линию.
- (Необязательно) Введите значение и нажмите Введите , чтобы изменить угол направляющей линии (относительно начальной линии). Вы можете ввести десятичное значение, например 34.1 , или наклон, например 1: 6 . Измените это значение сколько угодно раз, пока не сделаете другой выбор или не выберете другую команду.
Примечание. SketchUp может обрабатывать до 0,1 градуса угловой точности.
Редактирование направляющих линий
Чтобы изменить ориентацию направляющей линии или направляющей точки, вы можете переместить или повернуть ее. Подробности см. В разделах «Перемещение объектов вокруг» и «Переворачивание и вращение».
Примечание: Вы не можете изменить размер направляющей линии, потому что направляющие линии бесконечны по длине.
Скрытие и стирание направляющих линий
Направляющие обычно создаются как временное вспомогательное средство для построения части вашей модели. Сохранение слишком большого количества направляющих линий в вашей модели может снизить точность вывода SketchUp и производительность отображения, поэтому вы можете скрыть направляющие линии во время работы или удалить все направляющие линии после завершения 3D-модели.
Чтобы скрыть направляющие линии, вы можете использовать один из следующих методов:
- С помощью инструмента Select () выберите одну или несколько направляющих, а затем выберите Edit> Hide .
- Щелкните контекстным щелчком выбранную направляющую или направляющие и выберите Hide из появившегося меню, как показано на рисунке.
Чтобы снова сделать скрытые направляющие видимыми, выберите Правка> Показать и выберите параметр в подменю «Показать».
Удаление направляющих линий полностью удаляет их и больше никогда не будет. Вот несколько способов удалить направляющие линии:
- С помощью инструмента Select () выберите одну или несколько направляющих, а затем выберите Edit> Delete .
- Щелкните руководство и выберите Стереть в появившемся меню.
- Щелкните направляющую линию с помощью инструмента Eraser ().
- Выберите Правка> Удалить направляющие , чтобы удалить все направляющие в текущем контексте.
Точная оценка высоты здания
Если вы не знаете высоту существующего здания, которое пытаетесь смоделировать, вот несколько методов, которые вы можете использовать, чтобы сделать обоснованное предположение:
- Подсчитать повторяющиеся единицы.
- Сделать снимок с объектом известной высоты
- Использовать тригонометрию.
Когда вы будете готовы выдавить контуры здания до нужной высоты, убедитесь, что вы находитесь в представлении ISO, выбрав Камера> Стандартные виды> ISO . Затем используйте инструмент Push / Pull (), чтобы выдавить здание в 3D и ввести точную высоту здания.
Метод 1. Подсчет повторяющихся единиц
Часто здания строятся из кирпича, блоков или других модульных строительных материалов.Измерьте высоту одного блока, подсчитайте общее количество блоков на фасаде и умножьте его, чтобы получить приблизительную общую высоту.
Этот метод также работает для всех уровней здания. Если вы можете измерить один уровень на фасаде вашего здания, вы можете умножить его на общее количество уровней, чтобы получить приблизительное общее измерение.
Метод 2: сфотографировать объект известной высоты
Когда вы делаете снимок здания, которое планируете смоделировать, включите на снимок что-нибудь (или кого-нибудь), высота которого вам известна.
Совет: Вот несколько советов по оценке высоты здания с помощью этого метода:
- Метрная палка или человек работает хорошо.
- Для точности разместите «известное количество» как можно ближе к зданию.
- Сделайте снимок как можно дальше, чтобы минимизировать вертикальное искажение.
Вы можете использовать программу для редактирования фотографий, чтобы оценить высоту вашего здания на основе объекта (или человека), который вы включили в фотографию.
Метод 3. Используйте простую тригонометрию
С помощью нескольких простых измерений можно с некоторой точностью оценить высоту. Взгляните на рисунок ниже. Все, что вам нужно знать:
- Ваше расстояние от дома
- Высота ваших глаз
- Угол между землей и верхом здания
Используйте эту формулу для расчета высоты здания:
Высота = (загар (угол) x расстояние) + высота глаз
Например, при расстоянии до здания 25 метров, угле 37 градусов и высоте глаз 1.75 метров, формула будет такой:
Высота = коричневый (37) x 25 м + 1,75 м
= 0,75355 x 25 м + 1,75 м
= 20,6 м
Примечание: На вашем калькуляторе кнопка загара вычисляет тангенс угла.
Краткий справочник измерительной коробки
В этом разделе вы найдете таблицы, в которых перечислены все значения, которые принимает поле «Измерения», в зависимости от того, какой инструмент вы используете. Помните, что после использования инструмента вы можете просто ввести значение и нажать Введите .Вам не нужно нажимать на поле «Измерения». Кроме того, пока вы не внесете еще одно изменение в свою модель или не выберете другой инструмент, вы можете продолжать вводить значения, которые изменяют ваше действие.
Указание единиц измерения
В следующей таблице показано, как указать единицы измерения. Если вы не укажете единицу измерения, SketchUp использует единицы из вашего шаблона. Чтобы просмотреть или изменить единицы измерения по умолчанию, выберите Окно > Информация о модели и выберите Единицы на боковой панели слева.
| Шт. | Как это указать | Пример |
|---|---|---|
| дюймов | + « | 10 ” |
| футов | + ’ | 10 ’ |
| Миллиметры | + мм | 10 мм |
| Сантиметров | + см | 10 см |
| Метры | номер + м | 10 мес. |
Создание массивов
Массив выстраивает геометрию в линию (линейный массив , ) или вокруг точки (радиальный массив , ).Вы создаете массив, когда копируете геометрию с помощью инструмента «Перемещение» или инструмента «Повернуть». В следующей таблице перечислены все модификаторы, которые вы можете использовать при создании массивов.
| Тип массива | Как это указать | Пример | Шаг |
|---|---|---|---|
| Внешний | + x | 3x | Равное расстояние как у оригинала, так и у исходной копии |
| Внешний | + * | 3 * | Равное расстояние как у оригинала, так и у исходной копии |
| Внутренний | + / | 3/ | Равное расстояние между оригиналом и исходной копией |
Ввод значений измерения для конкретного инструмента
Сразу после использования инструмента вы можете ввести точные значения, которые появятся в поле «Измерения».Значения, которые вы можете ввести, зависят от инструмента.
Примечание: Точный формат разделителя списка может отличаться в зависимости от региональных настроек вашего компьютера. Для европейских пользователей символ разделителя списка может быть точкой с запятой вместо запятой.
Следующие ссылки указывают на статью, в которой описаны допустимые значения и модификаторы для каждого инструмента:
7 отличных способов, с помощью которых рулетка может упростить работу по дому
unsplash
Скромная рулетка имеет множество функций, облегчающих вашу работу, и они скрыты у всех на виду.
Вы умеете пользоваться рулеткой?
Я думал, что да, пока человек в TikTok не показал мне, что я всю жизнь сгибал ленту под углом 90 градусов, когда она ударяется о стену — зря.
Измерительная лента — обманчиво простое устройство, имеющее важную цель — точно измерять предметы. Но у него есть несколько функций, призванных упростить эту работу, скрытые на виду.
Посмотрите, о скольких из них вы знали …
ПРОЧИТАЙТЕ БОЛЬШЕ:
* Стул Bunnings, которым «одержимы» австралийские поклонники декора, находится здесь
* Недорогое отопление: 7 способов согреть ваш дом за 50 долларов или меньше
* Удовольствие своими руками: удовольствие от прогулки в строительный магазин через 7 недель
ЛЕНТОЧНЫЙ КОРПУС
Вам когда-нибудь приходилось получать точные измерения в ограниченном пространстве?
Вы аккуратно протянули ленту по длине пола, стены или окна, а затем согнули ее под углом 90 градусов, потому что основание рулетки мешало?
Что ж, вы почувствуете себя немного глупо.
Ken Long / TIKTOK
Не сгибайте ленту у стены. Прибавьте размер ленты к длине измеряемого пространства.
Изгибать ленту не нужно, так как на ней уже напечатана длина меры.
Консультант по ремонту Кен Лонг поделился простым советом на TikTok.
«Почти каждая рулетка показывает расстояние отсюда до отсюда», — говорит он, указывая на обе стороны.
Все, что вам нужно сделать, это добавить число ширины к вашему измерению, и вы получите точное измерение с половиной хлопот.
Материал
Корпус ленты можно найти в небольшом прямоугольнике у основания.
Это очень полезно при измерении внутри окна или в других местах, где вы можете быть ограничены.
Представитель Mitre 10 Лиза Уилсон говорит, что ленточный корпус является обычным явлением, но не у всех метрических рулеток он есть.
«Некоторые рулетки серии Mitre 10 имеют эту функцию, но не все. На самом деле у нас есть метрическая версия той же самой ленты, которая используется в видео TikTok, которая есть, и это наша самая продаваемая эксклюзивная модель.»
В буннингах есть 8-метровая и 10-метровая рулетка с ленточными маркерами на корпусах. У более дешевых моделей ее нет.
THE CURVE
Stuff
Кривая помогает цифрам выделяться среди
Вы когда-нибудь задумывались, почему лезвие вашей рулетки изогнуто?
Вогнутая конструкция помогает удерживать лезвие жестким в выдвинутом состоянии. Изгиб также позволяет выделять числа на лезвии, чтобы помочь вам прочитать измерения .
ГВОЗДЬ / ВИНТ
Материал
На конце крючка каждой рулетки есть небольшая прорезь.
Небольшая прорезь в середине крючка на конце рулетки предназначена для удержания головки гвоздя или винта.
Идея состоит в том, чтобы удерживать конец на месте, если вы один и у вас нет другого человека, который бы удерживал другой конец. Вставьте его и вперед.
ИДЕАЛЬНЫЕ КРУГИ
Забудьте о попытках нарисовать круг от руки и в лучшем случае получить шаткий овал.Прикрепите конец рулетки к гвоздю, чтобы он оставался на месте, возьмите карандаш на нужном вам размере и используйте его, чтобы нарисовать идеальный круг.
РЕГУЛИРУЕМЫЙ КОНЕЦ
Материал
Первый дюйм ленты намеренно короткий, чтобы учесть «истинный ноль».
Металл на конце измерительной ленты намеренно покачивается.
Первый дюйм ленты короче 1/16 дюйма. Это не ошибка, это означает, что вы получите точные показания независимо от того, измеряете ли вы внутреннюю или внешнюю кромку поверхности.
Металлический наконечник имеет толщину ровно 1/16 дюйма.
Таким образом, если вы сделаете внутреннее измерение — прижав загнутый конец к объекту, который вы измеряете, — вы получите точное измерение.
Если зацепить конец за предмет, который вы измеряете, пространство в заклепках сдвинет крючок на 1/16 дюйма между крючком и лентой для компенсации.
Эта функция известна как истинный ноль.
ВЕРХНИЙ КРЮК
Материал
Рулетка со странным крючком предназначена для захвата чего угодно в любом направлении.
У некоторых рулеток есть странный крючок на другой стороне.
Они предназначены для крепления к любой поверхности в любом направлении, что упрощает измерение предметов в труднодоступных местах.
ИНСТРУМЕНТ ДЛЯ РАЗБОРКИ
123RF
У некоторых рулеток есть крючки с зубчатым краем, которые могут пригодиться для разметки измерений.
Распространенная ошибка заключается в том, что все измеряется идеально, только для того, чтобы помнить, что вам нужен способ пометить измерение.Но карандаша под рукой нет.
У некоторых рулеток есть крючки с зазубринами, предназначенные для замены одного. Если край крючка на вашей рулетке зазубрен, вы можете использовать саму меру, чтобы сделать легкую отметку на дереве или стене.
Простой способ проверить квадрат
Один из старейших приемов в книге по деревообработке — это, так сказать, простой метод определения того, когда какая-либо сборка или предмет имеет квадратную форму. Этот базовый трюк на самом деле вовсе не уловка; он основан на теореме Пифагора, которая гласит: «Сумма квадратов двух сторон прямоугольного треугольника равна квадрату третьей стороны или гипотенузе.»
Как проверить квадрат
Другими словами, если вы хотите определить, является ли сборка квадратной, используя математику, выберите грань, которую вы хотите проверить на квадрат. Проверьте один угол сборки с обрамляющим или комбинированным квадратом, чтобы убедиться, что это прямой угол. Затем, используя рулетку, измерьте вдоль одного края от этого прямого угла, чтобы получить длину, и с помощью калькулятора умножьте это значение длины на само себя (или возведите значение длины в квадрат). Сохраните этот квадрат длины в памяти калькулятора.
Затем измерьте одну из кромок, прилегающих к кромке, которую вы измерили ранее, чтобы получить ширину сборки. Выполните ту же задачу, умножив это значение на само себя (или возведя значение в квадрат), а затем прибавьте его к исходному значению в памяти калькулятора. Теперь у вас есть половина уравнения.
Чтобы получить третье значение, измерьте по диагонали (без препятствий) от открытого конца длинного края до открытого конца широкого края. Это даст то, что называется гипотенузой.Умножьте саму гипотенузу на время, и если это значение совпадает с суммой двух сторон в квадрате (другими словами, значение, которое вы сохранили в памяти, ваша сборка будет квадратной.
Правило 3-4-5
В деревообработке это иногда называют правилом 3-4-5. Хотя вы всегда можете использовать правило 3-4-5 для определения квадрата в любом масштабе, когда вы выкладываете проект, есть более точный (и намного более быстрый) способ определить, является ли ваша почти завершенная сборка квадратной.
Измерьте диагонали рулеткой и проверьте, совпадают ли два расстояния. Если они равны, ваша сборка квадратная.
Показательный пример: взгляните на рисунок наружной двери с приподнятой панелью. Если мы измеряем от одного угла до противоположного по диагонали (как показано красной линией), а затем сравниваем это расстояние с противоположным диагональным измерением (как показано синей линией), два расстояния должны точно совпадать. Если они равны, сборка квадратная.
Что делать, если два диагональных измерения не совпадают? Отрегулируйте сборку. На изображении выше, если длина красной линии больше, чем длина синей линии, нажмите внутрь на два красных угла.