Кубатурник оцилиндрованного бревна — sky38.ru
- Главная
—
- Статьи
—
- Кубатурник
—
Кубатурник оцилиндрованного бревна
Кубатурник оцилиндрованного бревна
где А — ширина теплового паза, b — глубина компенсационного паза, D — диаметр оцилиндрованного бревна(ОЦБ), h- высота ряда, H — высота ОЦБ.
Объем одного бревна высчитывается по формуле: π* (1/2D)² • L
где π — это 3,14, D — диаметр бревна, L — длина бревна.
Таблица кубатуры ОЦБ, длина бревна 6000мм:
Диаметр ОЦБ D, мм
|
Паз ОЦБ A, мм
|
Высота ряда h, мм
|
Высота бревна Н, мм
|
Объем ОЦБ, м3
|
Площадь ОЦБ, м2
|
Кол-во ОЦБ в 1 м3, шт
|
|
140
|
70
| 121,2 | 130,6 |
0,09
|
1,453
|
11,1
|
|
160
|
80
| 138,5 | 149,2 |
0,12
|
1,662
|
8,29
|
|
180
|
90
| 155,8 | 167,9 |
0,15
|
1,869
|
6,55
|
|
200
|
100
| 173,2 | 186,6 |
0,19
|
2,078
|
5,31
|
|
220
|
110
| 190,5 | 205,2 |
0,23
|
2,286
|
4,39
|
|
240
|
120
| 207,8 | 223,9 |
0,27
|
2,493
|
3,69
|
|
260
|
130
| 225,1 | 242,5 |
0,32
|
2,701
|
3,14
|
|
280
|
140
| 242,4 | 261,2 |
0,37
|
2,908
|
2,71
|
|
300
|
150
| 259,8 | 279,9 |
0,42
|
3,117
|
2,36
|
|
320
|
160
| 277,1 | 298,5 |
0,48
|
3,325
|
2,07
|
|
340
|
170
| 294,4 | 317,2 |
0,54
|
3,532
|
1,84
|
|
360
|
180
| 311,7 | 335,8 |
0,61
|
3,74
|
1,64
|
Кубатурник древесины, бревен, брусьев, досок и других пиломатериалов
Толщина в верхнем отрубе, см. | Объем м³, при длине, м. | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 3 | 3,5 | 4 | 4,5 | 5 | 5,5 | 6 | 6,5 | 7 | 7,5 | 8 | 8,5 | 9 | |
| 14 | 0,052 | 0,061 | 0,073 | 0,084 | 0,097 | 0,110 | 0,123 | 0,135 | 0,150 | 0,164 | 0,179 | 0,195 | 0,21 |
| 16 | 0,069 | 0,082 | 0,095 | 0,110 | 0,124 | 0,140 | 0,155 | 0,172 | 0,189 | 0,200 | 0,220 | 0,240 | 0,26 |
| 18 | 0,086 | 0,103 | 0,120 | 0,138 | 0,156 | 0,175 | 0,194 | 0,210 | 0,230 | 0,25 | 0,28 | 0,3 | 0,32 |
| 20 | 0,107 | 0,126 | 0,147 | 0,170 | 0,190 | 0,210 | 0,23 | 0,26 | 0,28 | 0,30 | 0,33 | 0,36 | 0,39 |
| 22 | 0,130 | 0,154 | 0,178 | 0,200 | 0,230 | 0,250 | 0,28 | 0,31 | 0,34 | 0,37 | 0,40 | 0,43 | 0,46 |
| 24 | 0,157 | 0,184 | 0,210 | 0,240 | 0,270 | 0,300 | 0,33 | 0,36 | 0,40 | 0,43 | 0,47 | 0,50 | 0,55 |
| 26 | 0,185 | 0,210 | 0,250 | 0,280 | 0,320 | 0,350 | 0,39 | 0,43 | 0,46 | 0,50 | 0,54 | 0,58 | 0,63 |
| 28 | 0,220 | 0,250 | 0,290 | 0,330 | 0,370 | 0,410 | 0,45 | 0,49 | 0,53 | 0,58 | 0,63 | 0,67 | 0,72 |
| 30 | 0,25 | 0,29 | 0,33 | 0,38 | 0,42 | 0,47 | 0,52 | 0,56 | 0,61 | 0,66 | 0,72 | 0,78 | 0,83 |
| 32 | 0,28 | 0,33 | 0,38 | 0,43 | 0,48 | 0,53 | 0,59 | 0,64 | 0,70 | 0,76 | 0,82 | 0,88 | 0,94 |
| 34 | 0,32 | 0,37 | 0,43 | 0,49 | 0,54 | 0,60 | 0,66 | 0,72 | 0,78 | 0,85 | 0,92 | 0,98 | 1,06 |
| 36 | 0,36 | 0,42 | 0,48 | 0,54 | 0,60 | 0,67 | 0,74 | 0,80 | 0,88 | 0,95 | 1,02 | 1,10 | 1,18 |
| 38 | 0,39 | 0,46 | 0,53 | 0,60 | 0,67 | 0,74 | 0,82 | 0,90 | 0,97 | 1,05 | 1,13 | 1,22 | 1,30 |
| 40 | 0,43 | 0,50 | 0,58 | 0,66 | 0,74 | 0,82 | 0,90 | 0,99 | 1,07 | 1,16 | 1,25 | 1,35 | 1,44 |
| 42 | 0,47 | 0,56 | 0,64 | 0,73 | 0,81 | 0,90 | 1,0 | 1,08 | 1,18 | 1,28 | 1,38 | 1,48 | 1,58 |
| 44 | 0,52 | 0,61 | 0,70 | 0,80 | 0,89 | 0,99 | 1,09 | 1,20 | 1,30 | 1,40 | 1,51 | 1,62 | 1,73 |
| 46 | 0,57 | 0,67 | 0,77 | 0,87 | 0,94 | 1,08 | 1,19 | 1,31 | 1,41 | 1,53 | 1,65 | 1,77 | 1,90 |
| 48 | 0,62 | 0,73 | 0,84 | 0,95 | 1,06 | 1,18 | 1,30 | 1,41 | 1,54 | 1,67 | 1,80 | 1,93 | 2,07 |
В таблице дана выборка наиболее популярных размеров бревен.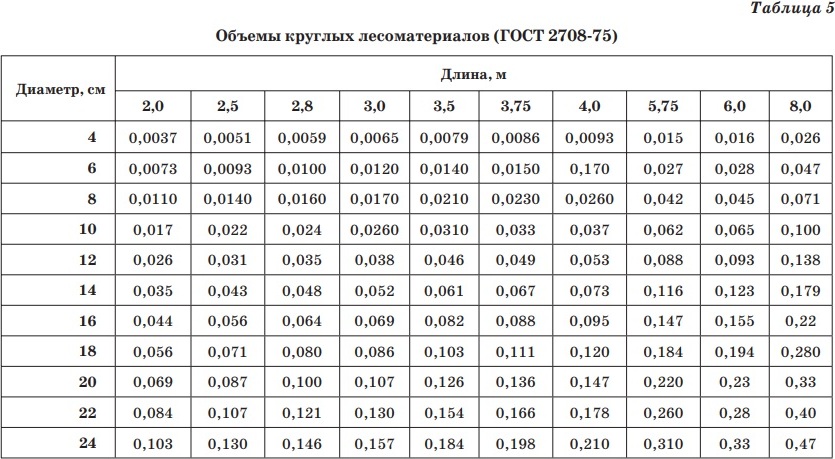 Если Вы хотите посмотреть более подробный кубатурник, то он отображен в ГОСТ 2708-75 «Лесоматериалы круглые. Таблицы объемов».
Если Вы хотите посмотреть более подробный кубатурник, то он отображен в ГОСТ 2708-75 «Лесоматериалы круглые. Таблицы объемов».
| D, мм | B, мм | L, м | V, м³ | B, мм | L, м | V, м³ | B, мм | L, м | V, м³ |
|---|---|---|---|---|---|---|---|---|---|
| 180 | 90 | 6,39 | 0,162 | 108 | 6,94 | 0,177 | 120 | 7,41 | 0,188 |
| 200 | 100 | 5,75 | 0,180 | 120 | 6,25 | 0,196 | 133 | 6,67 | 0,209 |
| 220 | 110 | 5,22 | 0,199 | 132 | 5,68 | 0,216 | 147 | 6,06 | 0,230 |
| 240 | 120 | 4,79 | 0,217 | 144 | 5,21 | 0,236 | 160 | 5,56 | 0,251 |
| 260 | 130 | 4,42 | 0,235 | 156 | 4,81 | 0,255 | 173 | 5,13 | 0,272 |
| 280 | 140 | 4,11 | 0,253 | 168 | 4,46 | 0,275 | 187 | 4,76 | 0,293 |
| 300 | 150 | 3,83 | 0,271 | 180 | 4,17 | 0,294 | 200 | 4,44 | 0,314 |
| 320 | 160 | 3,59 | 0,289 | 192 | 3,91 | 0,314 | 213 | 4,17 | 0,335 |
| 340 | 170 | 3,38 | 0,307 | 204 | 3,68 | 0,334 | 227 | 3,92 | 0,356 |
| 360 | 180 | 3,19 | 0,325 | 216 | 3,47 | 0,353 | 240 | 3,70 | 0,377 |
| 380 | 190 | 3,02 | 0,343 | 228 | 3,29 | 0,373 | 253 | 3,51 | 0,398 |
| 400 | 200 | 2,87 | 0,361 | 240 | 3,13 | 0,393 | 267 | 3,33 | 0,419 |
D — диаметр профилированного бревна;
B — ширина продольного паза;
L — количество погонных метров профилированного бревна необходимых для строительства одного квадратного метра стены сруба дома;
V— объем бревна на строительство одного квадратного метра стены сруба дома
| Ширина, мм | Толщина, мм | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 50 | 60 | 75 | 100 | 130 | 150 | 180 | 200 | 220 | 250 | |
| 130 | 0,065 | 0,078 | 0,0975 | 0,13 | ||||||
| 150 | 0,075 | 0,09 | 0,0113 | 0,15 | 0,195 | 0,225 | ||||
| 180 | 0,09 | 0,108 | 0,0135 | 0,18 | 0,234 | 0,27 | 0,324 | |||
| 200 | 0,1 | 0,12 | 0,015 | 0,2 | 0,26 | 0,3 | 0,4 | |||
| 220 | 0,11 | 0,132 | 0,0165 | 0,22 | 0,395 | 0,434 | ||||
| 250 | 0,125 | 0,15 | 0,188 | 0,25 | 0,5 | 0,625 | ||||
| Толщина, мм | Ширина, мм | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| 16 | 75 | 100 | 125 | 150 | |||||
| 19 | 75 | 100 | 125 | 150 | 175 | ||||
| 22 | 75 | 100 | 125 | 150 | 175 | 200 | 225 | ||
| 25 | 75 | 100 | 125 | 150 | 175 | 200 | 225 | 250 | 275 |
| 32 | 75 | 100 | 125 | 150 | 175 | 200 | 225 | 250 | 275 |
| 40 | 75 | 100 | 125 | 150 | 175 | 200 | 225 | 250 | 275 |
| 44 | 75 | 100 | 125 | 150 | 175 | 200 | 225 | 250 | 275 |
| 50 | 75 | 100 | 125 | 150 | 175 | 200 | 225 | 250 | 275 |
| 60 | 75 | 100 | 125 | 150 | 175 | 200 | 225 | 250 | 275 |
| 75 | 75 | 100 | 125 | 150 | 175 | 200 | 225 | 250 | 275 |
| 100 | 100 | 125 | 150 | 175 | 200 | 225 | 250 | 275 | |
| 125 | 125 | 150 | 175 | 200 | 225 | 250 | |||
| 150 | 150 | 175 | 200 | 225 | 250 | ||||
| 175 | 175 | 200 | 225 | 250 | |||||
| 200 | 200 | 225 | 250 | ||||||
| 250 | 250 | ||||||||
Более подробно с градацией хвойного сортамента Вы можете ознакомиться в ГОСТе 24454-80. Номинальные размеры длины пиломатериалов устанавливают от 1,0 до 6,5 м с градацией 0,25 м. При целевом заказе на пилораме, допускается изготавливать пиломатериалы с размерами сечения, не указанными в таблице и длиной более 6,5 м, вплоть до 9 м.
Номинальные размеры длины пиломатериалов устанавливают от 1,0 до 6,5 м с градацией 0,25 м. При целевом заказе на пилораме, допускается изготавливать пиломатериалы с размерами сечения, не указанными в таблице и длиной более 6,5 м, вплоть до 9 м.
А если Вам необходимо посчитать кубатуру дров то можно ознакомиться с нашей статьей.
Дрова мы по прежнему возим, обращайтесь.
кубатура · PyPI
Статус действий Github:
Статус покрытия:
Что такое кубатура?
Метод численного интегрирования. Из MathWorld
http://mathworld.wolfram.com/Cubature.html, Уберхубер (1997, стр. 71) и
Кроммер и Уберхубер (1998, стр. 49 и 155-165) используют слово «квадратура» для
означает численное вычисление одномерного интеграла, а «кубатура» означает
численное вычисление кратного интеграла.
Cubature для Python
Это оболочка для C-пакета профессора Стивена Джонсона, доступная по адресу https://github.com/stevengj/cubature.
Текущая версия представляет собой оболочку версии 1.0.4 пакета профессора Джонсона.
Документация
См. документацию модуля здесь http://saullocastro.github.io/cubature.
Оболочка Python для пакета Cubature
Из Wiki Nanostructures and Computation в Массачусетском технологическом институте
http://ab-initio.mit.edu/wiki/index.php/Cubature, Стивен В. Джонсон
http://math.mit.edu/~stevenj написал простой пакет C для адаптивного
многомерное интегрирование (кубатура) вектор-функций по
гиперкубы, и это оболочка Python для упомянутого пакета C.
Установка из исходного кода
У вас должен быть установлен Cython. Затем выполните:
python setup.py install
или (обычно в Linux):
установка python3 setup.py
Установка из репозитория pip
Просто выполните:
python -m pip install cubature
или (обычно в Linux):
python3 -m pip install cubature
Запуск тестов
Для запуска тестов необходимо загрузить исходный код. После установки как
После установки как
как описано выше, перейдите в корневую папку исходного кода и запустите:
ру.тест .
Оболочка Python была проверена с использованием тестовых интегралов из C
пакет и некоторые дополнительные функции тестирования от Genz. Подынтегральные выражения
были реализованы в Cython и проверены с помощью Mathematica.
Ссылка на эту оболочку Python для Cubature
Просим вас правильно цитировать эту библиотеку Python. Кроме того, было бы
полезно, если бы вы могли процитировать документы, в которых этот метод применялся как
хорошо.
Кастро, С.Г.П.; Лукьянов, А.; и другие. «Оболочка Python для Cubature: адаптивная многомерная интеграция». DOI: 10.5281/zenodo.2541552. Версия 0.17.2, 2023 г.
Ссылки на документы, использующие эту оболочку Python для Cubature
Используется для интеграции матриц касательной жесткости в вычислительной механике твердого тела
Castro, S.G.P. и другие. «Оценка нелинейных нагрузок на изгиб геометрически несовершенных составных цилиндров и конусов методом Ритца». Композитные конструкции, Vol. 122, 284-299, 2015.
Композитные конструкции, Vol. 122, 284-299, 2015.
Castro, S.G.P. и другие. «Полуаналитический подход к линейному и нелинейному анализу неподкрепленных многослойных композитных цилиндров и конусов при осевых нагрузках, скручивании и давлении». Тонкостенные конструкции, Vol. 90, 61-73, 2015.
Примеры
Некоторые примеры приведены в «./examples» https://github.com/saullocastro/cubature/tree/master/examples.
Расколите меня!
Вы можете разветвить этот репозиторий и модифицировать его любым удобным для вас способом.
хотеть. Также было бы неплохо, если бы вы могли отправить запрос на включение сюда на случай, если
вы думаете, что ваши модификации ценны для другого человека.
Лицензия
Эта оболочка соответствует условиям лицензии GNU-GPL Стивена Г. Джонсона, описанным в Пакет C _.
Кубатурный фильтр Калмана Обучение гибридных дифференциальных уравнений рекуррентных физиологических динамических моделей нейронной сети
- Список журналов
- Рукописи авторов HHS
- PMC99
Являясь библиотекой, NLM предоставляет доступ к научной литературе. Включение в базу данных NLM не означает одобрения или согласия с
Включение в базу данных NLM не означает одобрения или согласия с
содержание NLM или Национальных институтов здравоохранения.
Узнайте больше о нашем отказе от ответственности.
Annu Int Conf IEEE Eng Med Biol Soc. Авторская рукопись; доступно в PMC 2023 6 февраля.
Опубликовано в окончательной редакции как:
Annu Int Conf IEEE Eng Med Biol Soc. 2021 ноябрь; 2021: 763–766.
doi: 10.1109/EMBC46164.2021.9631038
PMCID: PMC99
NIHMSID: NIHMS1868070
PMID: 3489140 2
, 1 , 1 , 1 , 1 , 2 , 3 , 4 и 1
Информация об авторе Информация об авторских правах и лицензии Отказ от ответственности
Моделирование биологических динамических систем является сложной задачей из-за взаимозависимости различных системных компонентов, некоторые из которых не до конца изучены. Чтобы заполнить существующие пробелы в нашей способности механически моделировать физиологические системы, мы предлагаем объединить нейронные сети с моделями, основанными на физике. В частности, мы демонстрируем, как мы можем аппроксимировать отсутствующие обыкновенные дифференциальные уравнения (ОДУ) в сочетании с известными ОДУ, используя методы байесовской фильтрации для обучения параметров модели и одновременной оценки динамических переменных состояния. В качестве учебного случая мы используем хорошо изученную модель кровообращения в сетчатке человека и заменяем одну из ее основных ОДУ приближением нейронной сети, представляя случай, когда у нас есть неполные знания о динамике физиологического состояния. Результаты показывают, что динамика состояния, соответствующая отсутствующим ОДУ, может быть хорошо аппроксимирована с помощью нейронной сети, обученной с использованием подхода рекурсивной байесовской фильтрации в сочетании с известными динамическими дифференциальными уравнениями состояния.
Чтобы заполнить существующие пробелы в нашей способности механически моделировать физиологические системы, мы предлагаем объединить нейронные сети с моделями, основанными на физике. В частности, мы демонстрируем, как мы можем аппроксимировать отсутствующие обыкновенные дифференциальные уравнения (ОДУ) в сочетании с известными ОДУ, используя методы байесовской фильтрации для обучения параметров модели и одновременной оценки динамических переменных состояния. В качестве учебного случая мы используем хорошо изученную модель кровообращения в сетчатке человека и заменяем одну из ее основных ОДУ приближением нейронной сети, представляя случай, когда у нас есть неполные знания о динамике физиологического состояния. Результаты показывают, что динамика состояния, соответствующая отсутствующим ОДУ, может быть хорошо аппроксимирована с помощью нейронной сети, обученной с использованием подхода рекурсивной байесовской фильтрации в сочетании с известными динамическими дифференциальными уравнениями состояния. Это демонстрирует, что динамику и влияние отсутствующих переменных состояния можно зафиксировать с помощью совместной оценки состояния и оценки параметров модели в рамках рекурсивной байесовской оценки состояния (RBSE). Результаты также показывают, что этот подход RBSE к обучению параметров NN дает лучшие результаты (точность измерения/оценки состояния), чем обучение нейронной сети с обратным распространением во времени в тех же условиях.
Это демонстрирует, что динамику и влияние отсутствующих переменных состояния можно зафиксировать с помощью совместной оценки состояния и оценки параметров модели в рамках рекурсивной байесовской оценки состояния (RBSE). Результаты также показывают, что этот подход RBSE к обучению параметров NN дает лучшие результаты (точность измерения/оценки состояния), чем обучение нейронной сети с обратным распространением во времени в тех же условиях.
Ключевые слова: Рекуррентные нейронные сети, байесовская фильтрация, дифференциальные уравнения, кровообращение сетчатки. или молекулярные концентрации с течением времени. Такие модели основаны на известной физике описываемых систем и данных, полученных в результате экспериментов с людьми, животными, клеточными культурами, или комбинации таких данных в многомасштабных моделях. Сложные биологические системы состоят из множества взаимосвязанных процессов. Как правило, ОДУ для некоторых из этих процессов неизвестны, и могут возникнуть трудности с получением данных, необходимых для подбора параметров модели и формулирования математического выражения, лежащего в основе биофизики. Машинное обучение с учетом физики появилось как метод заполнения пробелов в моделях, основанных на дифференциальных уравнениях в целом. Например, Раисси и др. разработали систему глубокого обучения для решения задач, связанных с нелинейными дифференциальными уравнениями в частных производных [1], а Weinan et al. использовали глубокое обучение для решения многомерных параболических уравнений [2]. Хотя эти методы являются многообещающими, обучение глубокой нейронной сети, основанной на физике, может быть громоздким из-за длинных циклов и неизвестных начальных состояний, которые снижают эффективность обратного распространения во времени. Здесь мы представляем использование рекурсивной байесовской оценки и кубатурных фильтров Калмана для эффективного обучения рекуррентной нейронной сети, основанной на физике.
Машинное обучение с учетом физики появилось как метод заполнения пробелов в моделях, основанных на дифференциальных уравнениях в целом. Например, Раисси и др. разработали систему глубокого обучения для решения задач, связанных с нелинейными дифференциальными уравнениями в частных производных [1], а Weinan et al. использовали глубокое обучение для решения многомерных параболических уравнений [2]. Хотя эти методы являются многообещающими, обучение глубокой нейронной сети, основанной на физике, может быть громоздким из-за длинных циклов и неизвестных начальных состояний, которые снижают эффективность обратного распространения во времени. Здесь мы представляем использование рекурсивной байесовской оценки и кубатурных фильтров Калмана для эффективного обучения рекуррентной нейронной сети, основанной на физике.
Рекурсивная байесовская оценка — это вероятностный метод рекурсивной оценки функции плотности вероятности (PDF) путем извлечения информации о параметрах или состояниях динамической системы в реальном времени из измерений выходных данных системы и модели системы. Оценка состояния в данный момент времени основана на старой оценке этого состояния и новых данных измерений. Фильтры Калмана — это рекурсивные байесовские фильтры для многомерных нормальных распределений, которые обычно используются в обработке сигналов, навигации и автоматическом управлении. Использование фильтров Калмана для обучения рекуррентных нейронных сетей (RNN) было предложено и успешно реализовано в прошлом [3], [4]. Здесь мы представляем первую реализацию RNN, обученных фильтром Калмана, для оценки отсутствующих ОДУ в моделях сложных биологических систем.
Оценка состояния в данный момент времени основана на старой оценке этого состояния и новых данных измерений. Фильтры Калмана — это рекурсивные байесовские фильтры для многомерных нормальных распределений, которые обычно используются в обработке сигналов, навигации и автоматическом управлении. Использование фильтров Калмана для обучения рекуррентных нейронных сетей (RNN) было предложено и успешно реализовано в прошлом [3], [4]. Здесь мы представляем первую реализацию RNN, обученных фильтром Калмана, для оценки отсутствующих ОДУ в моделях сложных биологических систем.
Мы используем проверенную модель кровообращения в сетчатке человека для проверки нашего метода [5]. Мы сравниваем предлагаемый нами метод с традиционным методом, т. е. с обратным распространением во времени (BPTT), для различных уровней аддитивного шума. Результаты показывают, что наш метод был успешным в оценке поведения системы с NRMSE 0,038 и превосходил обратное распространение для всех протестированных параметров.
A. Кубический фильтр Калмана
В этой статье мы обучаем гибридную модель ОДУ и нейронной сети, используя рекурсивную байесовскую оценку состояния. В частности, когда модели прогнозирования и наблюдения являются линейными и гауссовскими, интегралы апостериорной рекурсии состояния могут быть решены аналитически, что приводит к известным уравнениям времени Калмана и обновлению измерений [6]. Когда используются нелинейные модели, требуемые интегралы часто становятся трудноразрешимыми, и приходится искать численные стратегии. Альтернативы включают линеаризацию нелинейных функций (расширенные фильтры Калмана, EKF) или методы выборки, такие как фильтры частиц [7], неароматизированные фильтры Калмана (UKF) [8] или кубатурные фильтры Калмана (CKF) [9].], которые предполагают разные уровни простоты системы. Например, EKF, UKF и CKF предполагают гауссовость моделей измерения и переходных моделей, в то же время обрабатывая интеграцию, используя эту гауссовость по-разному. В то время как EKF линеаризует модели, используя разложение Тейлора первого порядка, UKF и CKF используют неароматизированные и кубатурные правила для вычисления интегралов, таких как
I(ℓ)=∫𝒟ℓ(x)p(x)dx
(1)
где ℓ — нелинейная функция от x∈Rdx и p ( x ) = 𝒩( μ , Σ ) является гауссовской PDF со средним значением μ и ковариацией Σ 9 0136 , как взвешенная сумма оценок функций конечного числа детерминированных точек. Для кубатурного правила третьей степени интеграл в (1) может быть аппроксимирован как
Для кубатурного правила третьей степени интеграл в (1) может быть аппроксимирован как
I(ℓ)≈12dx∑j=12dxℓ(STξj+μ)
(2)
где ξj=[1]j2dx/2 — детерминированные точки [9], а S — нижнее треугольное разложение Холецкого такое, что Σ = СС ⊤ . Важно подчеркнуть, что кубатурное правило требует только две точки на измерение x , т. е. 2 d x , чтобы вычислить сумму в (2), что делает его более подходящим при работе в многомерные пространства состояний. Предполагая гауссовость апостериорных состояний, CKF может решать интегралы, необходимые для байесовской рекурсии, а также моменты (среднее значение и ковариация) нового апостериорного состояния [9].].
Напротив, фильтры частиц не предполагают какого-либо конкретного распределения, а аппроксимируют распределение линейной комбинацией дельт Дирака. Таким образом, моменты распространяющихся частиц могут быть легко вычислены. Одним из недостатков фильтров частиц является большое количество частиц, необходимое для точного представления распределения. Эта проблема сильно усугубляется, если размерность пространства состояний велика, что делает эту стратегию фильтрации неосуществимой в таких сценариях [10].
Одним из недостатков фильтров частиц является большое количество частиц, необходимое для точного представления распределения. Эта проблема сильно усугубляется, если размерность пространства состояний велика, что делает эту стратегию фильтрации неосуществимой в таких сценариях [10].
B. Обучение рекуррентных нейронных сетей с расширенным скрытым пространством
Байесовская фильтрация (BF) рассматривалась для обучения нейронных сетей, применяемых в динамических системах [11], с использованием EKF [12] и совсем недавно применялась для отслеживания целей в навигации внутри помещений [13], где модели перехода состояний и измерения могут быть произвольные нейронные сети с прямой связью, такие как:
с.=g(s,u;ω~)+n~y=q(s;ϕ)+r
(3)
где n~∼𝒩(0,σn~2I), s — вектор латентных состояний, u — внешние входы, r — аддитивный шум измерения с r∼𝒩(0,σr2I), а ω~ и ϕ — параметры модели g и q соответственно.
Дискретизированную модель можно получить путем аппроксимации производной с помощью конечных разностей, что приводит к
sk=sk−1+g(sk−1,uk−1;ω)+nk−1yk=q(sk;ϕ)+rk.
(4)
где мы предположили, что шаг по времени Δ t включен в веса NN, n k – шум процесса с nk∼𝒩(0,σn2I), где σn=∆tσn~, и r k 9010 0 — аддитивный шум измерения с rk∼𝒩(0 ,σr2I).
Чтобы узнать параметры модели, используя подход BF, мы увеличиваем скрытое пространство следующим образом:
ωk=ωk−1ϕk=ϕk−1sk=sk−1+g(sk−1,uk−1;ωk−1)+nk−1yk=q(sk;ϕk)+rk
(5)
который можно было бы переписать как
xk=f(xk−1,uk−1)+εk−1yk=h(xk)+rk
(6)
где xk=[ωkT,ϕkT,skT]T, f ( x k −1 , u 9 0099 к −1 ) = [ ω к -1 , ϕ к -1 , г ( с к 9 0100 −1 , u к −1 , ω к −1 )] ⊤ и h ( x k ) = q ( s к φ к ). Вышеупомянутая модель затем может быть рассмотрена с использованием методов фильтрации [12], [13], как описано в Разделе II-A.
Вышеупомянутая модель затем может быть рассмотрена с использованием методов фильтрации [12], [13], как описано в Разделе II-A.
C. Применение к кровообращению сетчатки
Предложенный подход был протестирован на утвержденной модели кровообращения сетчатки, предложенной Guidoboni et al. [5]. Модель состоит из четырех нелинейных ОДУ, описывающих кровоток через сосудистую сеть сетчатки и центральные сосуды сетчатки. Используя электрическую аналогию с потоком жидкости, электрические токи и электрические потенциалы представляют скорость кровотока и артериальное давление (9).0099 P ), а резисторы и конденсаторы представляют собой гидравлическое сопротивление и податливость сосуда [14]. Модель включает пять сосудистых компартментов, внутреннее давление которых обозначено цифрами от 1 до 5: центральная артерия сетчатки (ЦРА): P 1 ; артериолы: P 2 ; капилляры: P 3 ; венулы: P 4 ; центральная вена сетчатки (ЦВС): P 5 . Давление P в и P out — входное и выходное давление, которые управляют сетью. Применяя законы Кирхгофа для токов и напряжений и используя определяющие уравнения для каждого резистора и конденсатора, получается следующая система ОДУ:
Давление P в и P out — входное и выходное давление, которые управляют сетью. Применяя законы Кирхгофа для токов и напряжений и используя определяющие уравнения для каждого резистора и конденсатора, получается следующая система ОДУ:
P.1=ℱ1(P1,P2;Pin)
(7)
P.2=ℱ2(P1,P2,P4)
(8)
P.4=ℱ4(P2,P4, P5)
(9)
P.5=ℱ5(P4,P5;Pout)
(10)
Явные выражения функционала ℱ i , представляющие скорость изменения давления во времени P i , можно найти в [5]. Чтобы проверить предложенный нами метод, мы рассматриваем P 4 , как если бы его динамика была неизвестна, и заменяем ℱ 4 в уравнении (15) нейронной сетью со встроенным интегратором следующим образом
P.4=q4(P2,P4,P5;ω),
(11)
где q 4 — нейронная сеть прямого распространения с параметрами ω , а для динамики давлений использованы уравнения (7), (8) и (10) 5 . Заметим, что уравнения (7)-(10) имеют рекурсивные соотношения, которые становятся очевидными при дискретизации времени: с k +1 = с k 9 0100 + Δ т ж ( с k , u k ), где s состоит из четырех значений давления P i и f представляют функции в правой части уравнений ( 7), (8), (11) и (10). Следовательно, нейронная сеть, представленная в уравнении (11), обучается с использованием RNN, которая инкапсулирует это приближение дискретного времени для интегрирования по времени. В RNN переменные состояния используются для представления давления в каждом сосудистом отделе сетчатки. В качестве методов обучения можно использовать как обратное распространение во времени, так и кубатурные фильтры Калмана.
Заметим, что уравнения (7)-(10) имеют рекурсивные соотношения, которые становятся очевидными при дискретизации времени: с k +1 = с k 9 0100 + Δ т ж ( с k , u k ), где s состоит из четырех значений давления P i и f представляют функции в правой части уравнений ( 7), (8), (11) и (10). Следовательно, нейронная сеть, представленная в уравнении (11), обучается с использованием RNN, которая инкапсулирует это приближение дискретного времени для интегрирования по времени. В RNN переменные состояния используются для представления давления в каждом сосудистом отделе сетчатки. В качестве методов обучения можно использовать как обратное распространение во времени, так и кубатурные фильтры Калмана. В следующем разделе их выступления сравниваются. Нейронная сеть с прямой связью q 4 инкапсулируется в RNN, которая связывает известные дифференциальные уравнения с моделью NN для неизвестной динамики. q 4 , используемый в следующих численных анализах обучения BPTT и CKF, состоит из одного скрытого слоя с 20 скрытыми единицами и всего 103 параметрами. Для обучения BPTT мы использовали оптимизатор Adam со скоростью обучения 5 × 10 −3 .
В следующем разделе их выступления сравниваются. Нейронная сеть с прямой связью q 4 инкапсулируется в RNN, которая связывает известные дифференциальные уравнения с моделью NN для неизвестной динамики. q 4 , используемый в следующих численных анализах обучения BPTT и CKF, состоит из одного скрытого слоя с 20 скрытыми единицами и всего 103 параметрами. Для обучения BPTT мы использовали оптимизатор Adam со скоростью обучения 5 × 10 −3 .
Для моделей в (6) мы задаем вектор латентных состояний как дискретизированные значения давления в момент времени k , т. е. s k = [ P 1, k , …, 9009 9 П 5, к ] ⊤ , г ( s k ω k ) = [ℱ 1 9 0200 ( П 1, к , П 2, к Р в,к ), ℱ 2 ( П 1, К , П 2, К , П 4, к ), к 4 ( П 2 , к , п 4, к , п 5, к ; ω к ), ℱ 5 ( P 4 , к , П 5, к ; P out,k )], и h ( s k ) = 901 35 Hs k , где H — матрица с нулями и те, которые выбирают измеренные давления и блокируют ненаблюдаемые состояния. i,k−yi,k)2∕(nt(yimax−yimin))] ∕dy}1/2 соответственно с yk=[P1,k,…,P5,k]T∈Rdy и n t — общее количество использованных выборок времени.
i,k−yi,k)2∕(nt(yimax−yimin))] ∕dy}1/2 соответственно с yk=[P1,k,…,P5,k]T∈Rdy и n t — общее количество использованных выборок времени.
Давления P in и P out использовались в качестве входных данных, P 1 902 00 , P 2 и P 5 использовались в качестве наблюдаемых состояний для обучения модели и P 4 предполагалось, что оно не наблюдается и моделируется как скрытое пространство. Чтобы учесть потенциальный шум в системе, мы вводили белый шум во все входные данные и наблюдаемые состояния в наших экспериментах. Мы использовали пять различных уровней шума с отношениями сигнал-шум (SNR), приведенными на рис. , где также приведены результирующие количественные показатели ошибок. И MAPE, и NRMSE увеличивались с уменьшением SNR для CKF, а также для BPTT. При разных уровнях шума ошибки для BPTT составили 1,9. –5,4 раза выше, чем для CKF.
–5,4 раза выше, чем для CKF.
ТАБЛИЦА I
MAPE и NRMSE, усредненные по 100 экспериментам Монте-Карло
MAPE
NRMSE
NRMSE
Открыть в отдельном окне
— показать наземных истинных значений, т. е. значений, полученных с помощью ОДУ, предоставленных Guidoboni et al. [5] и оценки наблюдаемого и ненаблюдаемого состояний после обучения модели зашумленными значениями давления. представляет собой единственную симуляцию для модели, обученной CKF, демонстрирующую шум на входных данных и оценочные значения. Несмотря на наличие шума, оценочные значения быстро сходятся к истинным значениям. и продемонстрировать среднее и 95% доверительные интервалы для симуляций Монте-Карло с использованием обучения CKF () и BPTT () для симуляций с SNR 22,56. Для обоих методов оценочные значения сходятся к наземным истинным значениям. Однако модель, обученная CKF, способна оценивать ненаблюдаемое состояние за меньшее количество шагов с большей достоверностью, чем та же модель, обученная с помощью BPTT. представлены кривые обучения для обоих методов, показывающие, что обучение CKF достигает ошибки ниже уровня шума быстрее и сходятся за меньшее количество шагов, чем BPTT.
е. значений, полученных с помощью ОДУ, предоставленных Guidoboni et al. [5] и оценки наблюдаемого и ненаблюдаемого состояний после обучения модели зашумленными значениями давления. представляет собой единственную симуляцию для модели, обученной CKF, демонстрирующую шум на входных данных и оценочные значения. Несмотря на наличие шума, оценочные значения быстро сходятся к истинным значениям. и продемонстрировать среднее и 95% доверительные интервалы для симуляций Монте-Карло с использованием обучения CKF () и BPTT () для симуляций с SNR 22,56. Для обоих методов оценочные значения сходятся к наземным истинным значениям. Однако модель, обученная CKF, способна оценивать ненаблюдаемое состояние за меньшее количество шагов с большей достоверностью, чем та же модель, обученная с помощью BPTT. представлены кривые обучения для обоих методов, показывающие, что обучение CKF достигает ошибки ниже уровня шума быстрее и сходятся за меньшее количество шагов, чем BPTT.
Открыть в отдельном окне
Пример симуляции для модели, обученной CKF, с добавлением белого шума (SNR 22,56) к входным данным и наблюдаемым состояниям.
Открыть в отдельном окне
Результат обучения CKF на 100 симуляциях Монте-Карло с белым шумом (SNR 22,56). Показаны наземные истинные значения (сплошные линии) и оценочные значения (пунктирные линии) с 95% доверительными интервалами для всех оценочных состояний.
Открыть в отдельном окне
Результат обучения BPTT на 100 симуляциях Монте-Карло с белым шумом (SNR 22,56). Показаны наземные истинные значения (сплошные линии) и оценочные значения (пунктирные линии) с 95% доверительные интервалы для всех оцениваемых состояний.
Открыть в отдельном окне
Кривые обучения CKF и BPTT для моделирования с белым шумом (SNR 22,56). Результаты на обучающей выборке (сплошные линии) и тестовой выборке (штриховые линии) показаны в сравнении с уровнем шума (черная сплошная линия).
Экспериментальные результаты показывают, что модели RNN могут заполнить пробелы в моделировании физиологических моделей на основе ОДУ при условии, что набор входных и выходных данных модели можно наблюдать. В модели циркуляции сетчатки мы получили метрики ошибок в виде среднего абсолютного значения, достигающего пороговых значений ниже уровня шума. Сравнивая результаты CKF и BPTT, мы заметили, что CKF обеспечивает значительное улучшение как конвергенции обучения, так и производительности теста, что подтверждается результатами, представленными в и . Это связано с тем, что стратегии BF постоянно обновляют состояния всякий раз, когда доступно новое измерение. Хотя мы решили остановить обновление параметров RNN на этапе тестирования, на практике мы могли бы обновлять параметры бесконечно, позволяя модели, возможно, адаптироваться к физиологическим состояниям, не содержащимся в обучающем наборе.
В модели циркуляции сетчатки мы получили метрики ошибок в виде среднего абсолютного значения, достигающего пороговых значений ниже уровня шума. Сравнивая результаты CKF и BPTT, мы заметили, что CKF обеспечивает значительное улучшение как конвергенции обучения, так и производительности теста, что подтверждается результатами, представленными в и . Это связано с тем, что стратегии BF постоянно обновляют состояния всякий раз, когда доступно новое измерение. Хотя мы решили остановить обновление параметров RNN на этапе тестирования, на практике мы могли бы обновлять параметры бесконечно, позволяя модели, возможно, адаптироваться к физиологическим состояниям, не содержащимся в обучающем наборе.
Распространенной проблемой при решении ОДУ является определение начальных условий. Эта проблема сохраняется в гибридной схеме ODE-RNN, обсуждаемой в этой статье, особенно для модели, обученной с помощью BPTT. Теоретически это можно решить, включив начальные состояния в качестве дополнительных параметров модели, которые необходимо оценивать как на этапах обучения, так и на этапах тестирования. Однако при тестировании этого подхода нам так и не удалось получить точные оценки исходных физиологических состояний. С другой стороны, приняв подход BF, мы изменили перспективу проблемы с оценка предыдущего состояния с BPTT до оценка текущего состояния с учетом предыдущего набора измерений с CKF. Таким образом, в формулировке BF мы можем не учитывать начальные состояния, поскольку обновления фильтрации быстро перемещают состояния вблизи правильного значения. Это различие является ключевым при моделировании сложных систем, поскольку может потребоваться найти сотни или даже тысячи условий начального состояния.
Однако при тестировании этого подхода нам так и не удалось получить точные оценки исходных физиологических состояний. С другой стороны, приняв подход BF, мы изменили перспективу проблемы с оценка предыдущего состояния с BPTT до оценка текущего состояния с учетом предыдущего набора измерений с CKF. Таким образом, в формулировке BF мы можем не учитывать начальные состояния, поскольку обновления фильтрации быстро перемещают состояния вблизи правильного значения. Это различие является ключевым при моделировании сложных систем, поскольку может потребоваться найти сотни или даже тысячи условий начального состояния.
Аспекты реализации стратегии BF также важны, поскольку нелинейные системы часто приводят к численным подходам, которые плохо масштабируются с размерностью пространства состояний. Здесь мы рассмотрели кубатурные правила третьей степени для решения интегралов фильтрации в предположении гауссовости состояний. Кубатурные правила особенно интересны, поскольку число требуемых частиц относительно невелико (в два раза больше размерности пространства состояний) и детерминировано, а решение является точным для мономов степени три или меньше [9]. ]. Однако распространение таких частиц через модели перехода состояний и наблюдения приводит к множественным независимым оценкам модели, что резко увеличивает вычислительные затраты на процедуру оптимизации на этапе обучения. Тем не менее независимая оценка таких частиц позволяет легко распараллелить алгоритм.
]. Однако распространение таких частиц через модели перехода состояний и наблюдения приводит к множественным независимым оценкам модели, что резко увеличивает вычислительные затраты на процедуру оптимизации на этапе обучения. Тем не менее независимая оценка таких частиц позволяет легко распараллелить алгоритм.
В этой статье мы представили стратегию дополнения моделей на основе ODE с помощью RNN, где мы сравнили две разные методологии обучения: обратное распространение и байесовскую фильтрацию с CKF. Используя подтвержденную модель циркуляции сетчатки глаза человека, мы показали, что обе методики способны аппроксимировать отсутствующий ODE, и что CKF значительно превосходит BPTT из-за временных обновлений латентных состояний даже на этапе тестирования. Эти результаты показывают, что стратегии на основе BF обладают большим потенциалом для аппроксимации динамики неизвестных состояний в системах ОДУ.
Эта работа была частично поддержана NIH (OT2OD030524) и NSF (DMS-1853222/1853303, IIS-1715858, M3X-20040457).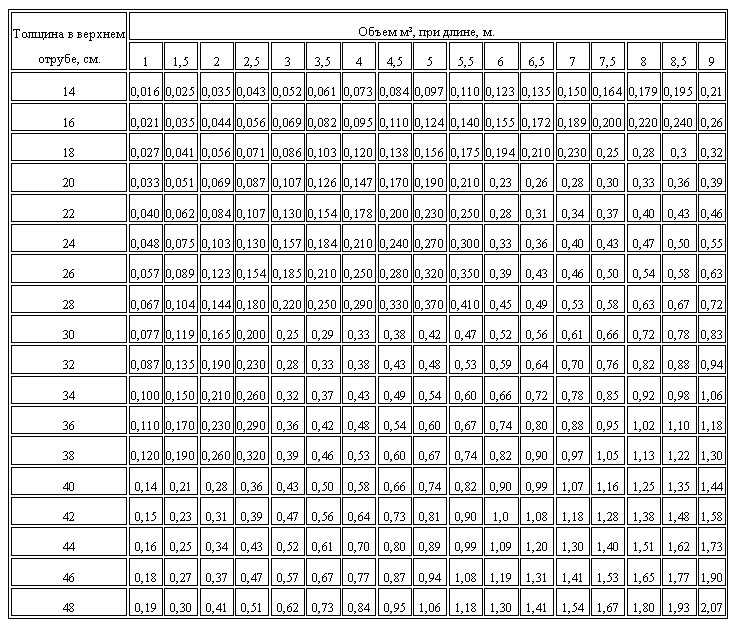
[1] Раисси М., Пердикарис П. и Карниадакис Г., «Физико-информированные нейронные сети: структура глубокого обучения для решения прямых и обратных задач, включающих нелинейные дифференциальные уравнения в частных производных», Журнал вычислительной физики, том. 378, стр. 686–707, 2019. [Онлайн]. Доступно: https://www.sciencedirect.com/science/article/pii/S0021999118307125 [Google Scholar]
[2] E W, Han J и Jentzen A, «Численные методы, основанные на глубоком обучении, для многомерных параболических дифференциальных уравнений в частных производных и обратных стохастических дифференциальных уравнений», Communications in Mathematics and Statistics, vol. 5, нет. 4, с. 349–380, ноябрь
2017. [Онлайн]. Доступно: 10.1007/s40304-017-0117-6 [CrossRef] [Google Scholar]
[3] Сингхал С. и Ву Л., «Обучение многослойных персептронов с помощью расширенного алгоритма Калмана», в Достижениях в области нейронных систем обработки информации, 1988, стр. 133–140. [Google Scholar]
[4] Пускориус Г. и Фельдкамп Л., «Развязанное расширенное обучение фильтра Калмана многоуровневых сетей с прямой связью», в материалах Международной объединенной конференции по нейронным сетям, 1991, стр. 771–777. [Google Scholar]
и Фельдкамп Л., «Развязанное расширенное обучение фильтра Калмана многоуровневых сетей с прямой связью», в материалах Международной объединенной конференции по нейронным сетям, 1991, стр. 771–777. [Google Scholar]
[5] Guidoboni G, Harris A, Cassani S, Arciero J, Siesky B, Amireskandari A, Tobe L, Egan P, Januleviciene I, and Park J, «Внутриглазное давление, артериальное давление и кровь сетчатки саморегуляция потока: математическая модель для выяснения их взаимосвязи и клинической значимости», Investigative Ophthalmology & Visual Science, vol. 55, нет. 7, стр. 4105–4118, 2014. [Бесплатная статья PMC] [PubMed] [Google Scholar]
[6] Саркка С. Байесовская фильтрация и сглаживание. Издательство Кембриджского университета, 2013, вып. 3. [Google Scholar]
[7] Арулампалам М.С., Маскелл С., Гордон Н. и Клапп Т. «Учебное пособие по фильтрам частиц для онлайн-нелинейного/негауссовского байесовского отслеживания», IEEE Transactions on signal processing, vol. 50, нет. 2, стр. 174–188, 2002. [Google Scholar]
174–188, 2002. [Google Scholar]
[8] Ван Э.А., Ван Дер Мерве Р., Хайкин С. Фильтр Калмана без запаха // Фильтрация Калмана и нейронные сети. 5, нет. 2007, стр. 221–280, 2001. [Google Scholar]
[9] Арасаратнам И. и Хайкин С., «Кубатурные фильтры Калмана», IEEE Transactions on Automatic Control, vol. 54, нет. 6, стр. 1254–1269, 2009. [Google Scholar]
[10] Имбириба Т. и Клосас П., «Улучшение фильтрации частиц с использованием гауссовских процессов», на 23-й Международной конференции IEEE по объединению информации (FUSION), 2020 г. IEEE, 2020 г., стр. 1–7. [Google Scholar]
[11] Хайкин С. Фильтрация Калмана и нейронные сети. Джон Вили и сыновья, 2004 г., том. 47. [Google Академия]
[12] Erdogmus D, Sanchez JC и Principe JC, «Метод на основе модифицированного фильтра Калмана для обучения многослойных персептронов с рекуррентным состоянием», в материалах 12-го семинара IEEE по нейронным сетям для обработки сигналов. IEEE, 2002 г., стр. 219–228. [Google Scholar]
[13] Ву П.