Кубатурник лісу: Кубатурник круглого леса [Derevo.ua]

‎App Store: Кубатурник леса ГОСТ 2708-75

Описание

ФУНКЦИИ ПРИЛОЖЕНИЯ:
► объем круглых бревен по ГОСТ 2708-75
► объем оцилиндрованных бревен
► выбор любого диаметра и любой длины
► удобный ввод количества бревен (не нужно нажимать 40 раз)
► подсчет количества и объема бревен по каждому диаметру
► подсчет суммарного объема, количества и цены для каждой группы диаметров
► создание, редактирование, удаление и экспорт расчетов
► для каждого расчета: выбор валюты, клиента, даты отгрузки
► настройка цен для разных групп диаметров
► удобный выбор диаметров на панели: можно настроить выбор только четных или нечётных диаметров, а также диаметров с заданными номерами
► учет брака и балансов (по необходимости)
► выбор округления для оцилиндрованных бревен
► сохранение расчетов в приложении
► поиск и сортировка расчетов по разным параметрам: по типу, имени, клиенту, дате отгрузки или создания, объему
► экспорт данных в Excel или Google Таблицы
► скриншот итогов
► отправка файла или скриншота по почте, whatsApp или другим мессенджерам
► сохранение файла на устройстве или в iCloud
► передача файла через AirDrop
► добавление, изменение и удаление клиентов
► удобная помощь и оперативная техподдержка по почте
► NEW!!! Создание шаблонов для расчетов
► NEW!!! Удаление всех записей в расчете
► NEW!!! Замена длин для всех бревен в расчете
► NEW!!! Выбор сортировки бревен в Итогах: сортировка по Диаметру или по Длине бревен
► NEW!!! Выбор отображения бревен в Расчете: показывать сначала Диаметр, а потом Длину, либо наоборот: сначала Длину, а потом Диаметр
► NEW!!! Объединение нескольких расчетов в один расчет
► NEW!!! Выбор и Удаление нескольких расчетов
► NEW!!! Задать для всех новых расчетов диаметры и цены по умолчанию.

Объем по ГОСТ 2708-75:
Берется из стандарта «ГОСТ 2708-75. ЛЕСОМАТЕРИАЛЫ КРУГЛЫЕ. ТАБЛИЦЫ ОБЪЕМОВ». В приложении представлены объемы бревен:
— длиной от 1,0 до 9,5 м и толщиной от 3 до 120 см
— длиной от 0,5 до 0,9 м и толщиной от 6 до 15 см
— длиной от 10,0 до 13,5 м и толщиной от 8 до 38 см

Объем оцилиндрованных бревен:
Считается по формуле πr² • H, где:
π — 3,14
r² — радиус оцилиндр-го бревна в квадрате
r = D/2, где D — диаметр бревна
Н — длина оцилиндрованного бревна

1 апр. 2022 г.

Версия 4.2.0

ВНИМАНИЕ! Из-за санкций App Store больше не принимает платежи по карте. Теперь совершить покупку можно двумя способами.
► Способ 1: Настройте оплату через Мобильный телефон. Для этого откройте приложение Настройки -> Нажмите на Apple ID (Ваше имя) -> Оплата и доставка -> Добавить способ Оплаты -> Мобильный телефон. Убедитесь, что на счете Вашего телефона достаточно средств для покупки.
► Способ 2: Пополните Ваш счет Apple ID. Для этого откройте App Store → Профиль (человечек в правом верхнем углу) → Пополнить счет Apple ID. Если у Вас возникнут вопросы, напишите нам на почту [email protected], мы поможем!

Что нового в этой версии:
1) Добавлена функция «Задать диаметры и цены по умолчанию для всех новых расчетов». Для включения данной функции нажмите вкладку «Настройки приложения» в правом нижнем углу экрана, затем в Настройке «Цена по умолчанию за м3» введите нужные диаметры и цену для них.
2) Теперь в расчете данные диаметра, длины и количества выравниваются по центру.

Оценки и отзывы

Оценок: 34

Дмитрий

Отличный кубатурник, пользовался на андроиде, но таскать с собой второй телефон только из-за кубатурника надоело. Купил на айфон и не жалею)

Уровень на 5+

Кубатурник бревна отличнейший все ясно быстро и удобно ! Добавьте в нем и кубатуру Доски ! Цены вам не будет!)))

Большое спасибо за Ваш отзыв! Очень рады, что приложение удобное. Мы выпустили новое приложение «Кубатурник доски леса Pro ГОСТ», в нем очень много функций по расчету кубатуры, площади, погонных метров доски. Можно выбирать любые единицы измерения, удобно вводить цену, ширину, толщину, длину по умолчанию, также можно считать пильные и зачетные размеры по заданному коэффициенту потери, заданным допускам на усушку или по ГОСТ.
Будем рады, если Вы попробуете наше новое приложение и напишите, все ли Вас устраивает и нужны ли какие-либо дополнительные функции:)

Не доволен

Постоянно логает, уже в сохранённых списках меняет количество и диаметры самостоятельно.

1 июня 2020:
UPD: Добрый день! Версия 1.3.0. со всеми исправлениями уже доступна в App Store)
Мы будем очень признательны, если Вы напишите нам сюда или на почту (в нашем приложении Вкладка помощь -> кнопка Задать вопрос), если после обновления у Вас все же будут возникать проблемы в работе приложения.
Если же после обновления приложение будет работать корректно и без лагов, мы будем очень признательны, если Вы поставите нам более высокую оценку:)
Большое спасибо за внимание!
С уважением, команда разработчиков приложения «Кубатурник леса».
——
30 мая 2020:
Добрый день! Большое спасибо за Ваш ценный отзыв.
Мы исправили ошибку «уже в сохранённых списках меняет количество и диаметры самостоятельно». Данная ошибка возникала, когда Вы меняли количество или диаметр бревна через текстовое поле в одном расчете, а потом открывали другой расчет, и в нем также отображались измененные данные. Теперь эта проблема устранена и все работает исправно, пересохранений данных нет.
Также мы исправили вылетание программы в некоторых случаях: при изменении диаметра, количества и длины бревен в расчете, а также при изменении диаметров и цен в Настройках расчета. Теперь приложение работает стабильно, без лагов и вылетов.

Разработчик Alisa Potapova указал, что в соответствии с политикой конфиденциальности приложения данные могут обрабатываться так, как описано ниже. Подробные сведения доступны в политике конфиденциальности разработчика.

Сбор данных не ведется

Разработчик не ведет сбор данных в этом приложении.

Конфиденциальные данные могут использоваться по-разному в зависимости от вашего возраста, задействованных функций или других факторов. Подробнее

Информация

Провайдер

Alisa Potapova

Размер

26 МБ

Категория

Утилиты

Возраст

4+

Copyright

© Alisa Potapova 2022

Цена

179,00 ₽

• Поддержка приложения

• Политика конфиденциальности

Поддерживается

Другие приложения этого разработчика

Вам может понравиться

Таблица кубатурник пиломатериала, сколько штук бруса и доски в кубе

Таблица кубатурник доски, сколько досок в кубе

Таблица пиломатериала — кубатурник — сколько штук доски обрезной в кубе.

Таблица кубатурник бруса, сколько бруса в кубе

Таблица расчета кубатуры бруса — кубатурник — сколько штук бруса в кубе.

ЗАДАТЬ ВОПРОС

Остались вопросы? Напишите нам, мы ответим Вам в ближайшее время!

Библиотека Кубы — arXiv Vanity

Т. Хан

Институт физики им. Макса Планка

Föhringer Ring 6, D–80805 Мюнхен, Германия

Abstract

Концепции и реализация библиотеки Cuba для многомерных
разъясняется численное интегрирование.

1 Обзор

Куба [2] — это библиотека для многомерных числовых
интеграция. Он имеет четыре алгоритма интеграции с интерфейсами
для Фортрана, C/C++ и Mathematica. Все четыре могут интегрировать вектор
подынтегральные выражения и их вызов очень похожи, чтобы упростить
переключать подпрограммы для сравнения. Обобщаются основные характеристики
ниже.

Обычный:
Вегас

Доступны основные методы интеграции:

∙ проба Соболя (квази Монте-Карло)

∙ Образец Mersenne Twister (псевдо Монте-Карло)

Снижение отклонения:
выборка по важности

Обычный:
учтивый

Доступны основные методы интеграции:

∙ проба Соболя (квази Монте-Карло)

∙ Образец Mersenne Twister (псевдо Монте-Карло)

Снижение отклонения:
выборка по важности в сочетании с глобально адаптивным подразделением

Обычный:
Дивонн

Доступны основные методы интеграции:

∙ Проба Коробова (решеточный метод)

∙ проба Соболя (квази Монте-Карло)

∙ Образец Mersenne Twister (псевдо Монте-Карло)

∙ кубатурные правила (детерминированный метод)

Снижение отклонения:
стратифицированная выборка с использованием методов
численная оптимизация

Обычный:
Куре

Доступен базовый метод интеграции:

∙ кубатурные правила (детерминированный метод)

Снижение отклонения:
глобально адаптивное подразделение

Прежде чем объяснять модные словечки, встречающиеся в этом списке, возможно,
стоит ответить на два часто задаваемых вопроса.

Во-первых, численное интегрирование быстро усложняется с
увеличивающееся измерение, независимо от того, сколько трюков встроено в
интегратор. Чтобы проиллюстрировать это, представьте, что вы вычисляете объем
д-тусклый. сферы Sd путем интегрирования ее характеристической функции χ=θ(1−∥x∥2) внутри окружающего гиперкуба Cd=[−1,1]d. Таким образом, с точки зрения Монте-Карло отношение r=VolSd/VolCd можно рассматривать как вероятность того, что универсальная
интегратор найдет шар вообще. Цифры четко видны
то, что часто называют «проклятием размерности»:

Вторая, Куба (и, если уж на то пошло, самая многомерная
интеграторы) могут вычислять только интегралы Римана вида

Большинство вопросов касаются границ, хотя это просто
преобразовать конечную область интегрирования в единичный гиперкуб:

	∫b1a1⋯∫bdadddxf(→x)=∫10ddyJf(→x),		(3)
	J=d∏i=1(bi-ai),xi=ai+(bi-ai)yi.

2 концепции

2.1 Детерминистический анализ по сравнению с методом Монте-Карло 90 136

Куба содержит как детерминированные методы, так и методы интегрирования Монте-Карло.
Детерминированный подход основан на кубатурных правилах ,

со специально подобранными узлами →xi и весами wi.
Оценка ошибки выполняется, например. по нулевым правилам Nm (m

Оценка Монте-Карло, хотя и очень похожая по форме,

концептуально сильно отличается, поскольку эта формула обозначает
статистическое среднее по независимым и одинаково распределенным
случайные выборки →xi. В этом случае стандартное отклонение
дает вероятностную оценку ошибки интегрирования:

2.2 Построение правил кубатуры

Начиная с ортогонального базиса функций {b1,…,bm} –
обычно мономы — с которыми можно (надеюсь) аппроксимировать большинство f
достаточно хорошо, требуется, чтобы каждое bi интегрировалось точно по формуле
Cn: Ibi\tiny!=Cnbi. Это m уравнений моментов

для nd+n неизвестных →xi и wi. Они представляют грозный,
в общем случае нелинейная система уравнений. Дополнительные предположения, например. симметрии обычно необходимы для решения этой системы. на Кубе работают
правила Генца – Малика [3] , построенные из симметричного
мономиальная основа.

2.3 Глобально адаптивное подразделение

После того, как будет доступна оценка ошибки для интеграла, глобальная
адаптивность легко реализовать:

1. Интегрируем всю область: Итот±Этот.
   

2. , в то время как Etot>max(εrelItot,εabs)
   

3. Найдите область r с наибольшей ошибкой.
   

4. Разделить пополам (или иным образом разрезать) r.
   

5. Интегрировать каждый подрегион r отдельно.
   

6. Itot=∑Ii,
   Eобщ=√∑E2i.
   

7. конец, а

Здесь уместно сделать замечание о двух точностях, εrel и
εабс. Наивно навязывают относительную точность:
результат должен быть точным, скажем, до одной тысячной, т. е. εотн=10−3. Однако для интегральных значений, стремящихся к нулю,
эта цель становится все труднее и труднее достичь, и чтобы не тратить
чрезмерное количество времени в таких случаях, абсолютная точность
можно задать εабс, где обычно εабс≪εотн.

2.4 Выборка по важности

Выборка по важности вводит весовую функцию в интеграл:

с двумя требованиями:
а) нужно иметь возможность выбирать из распределения w(→x),
б) f/w должен быть «гладким» в том смысле, что
σw(f/w)<σ(f), например w и f должны иметь такая же пиковая структура.
Известно, что идеальным выбором является w(→x)=|f(→x)|/If, который
имеет σw(f/w)=0, но малопригоден, так как требует априорного
знание интегрального значения.

2.5 Стратифицированная выборка

Работа по стратифицированной выборке по субрегионам выборки. Рассмотрим в общей сложности
выборка n точек в области r=ra+rb по сравнению с выборкой n/2 точек
в ра и н/2 в рб. В последнем случае дисперсия равна

, тогда как в первом случае ее можно записать как

Даже в этом простом примере последняя дисперсия в лучшем случае равна
прежний, и только если интегральные значения идентичны. Оптимальный
можно показать, что уменьшение дисперсии происходит при na/nb=σaf/σbf [4] . Таким образом, рецепт состоит в том, чтобы разделить
область интегрирования на части с одинаковой дисперсией, а затем произвести выборку всех
части с одинаковым количеством очков.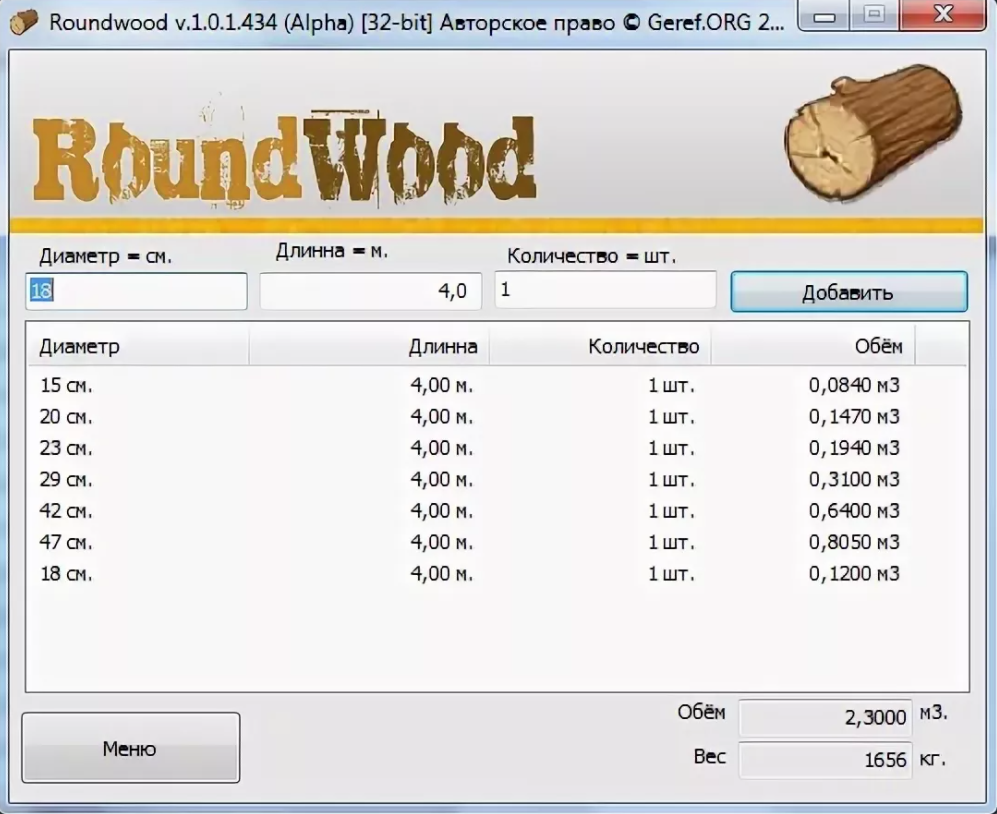

2.6 Методы квази-Монте-Карло 90–136

Методы квази-Монте-Карло основаны на неравенстве Коксмы–Главки.
который устанавливает верхнюю границу ошибки формулы интегрирования
Qnf=1n∑ni=1f(→xi),

Кроме выбора другого подынтегрального выражения мало что можно сделать
о V(f), «вариации в смысле Харди и Краузе».
невязка D∗ последовательности →x1,…,→xn
определяется как

где ν(r) подсчитывает →xi, попадающие в r. Слово
«равнораспределенный» действительно обычно означает, что ν(r) пропорциональна
к Волру. Квазислучайные последовательности могут быть построены с помощью
существенно более низкое несоответствие, чем (псевдо-)случайные числа. Монте
Алгоритм Карло, основанный на этих последовательностях, обычно достигает сходимости.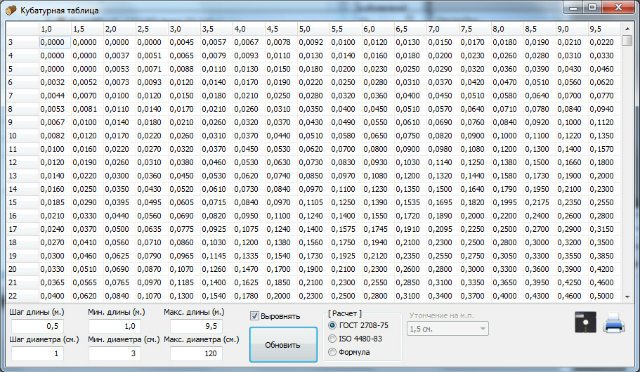
ставки O(logd−1n/n), а не обычные O(1/√n).

Куба предлагает на выбор квазислучайные последовательности Соболя [5] или
псевдослучайные последовательности Mersenne Twister [6] для всех
Алгоритмы Монте-Карло. Рисунок 1 показывает, что
квазислучайные числа покрывают плоскость гораздо более однородно, чем
псевдослучайные числа.

Рисунок 1: Сравнение последовательностей.

2.7 Методы решетки

Решетчатые методы требуют периодического подынтегрального выражения, обычно получаемого
применение преобразование периодизации (Кубинская Дивонна использует
х→|2x−1|). Отбор проб производится на интегрированной решетке L
натянутый на тщательно подобранный целочисленный вектор →z:

→z выбирается (путем обширных компьютерных поисков) для выбивания как
как можно больше «брегговских отражений» низкого порядка в члене ошибки
(см.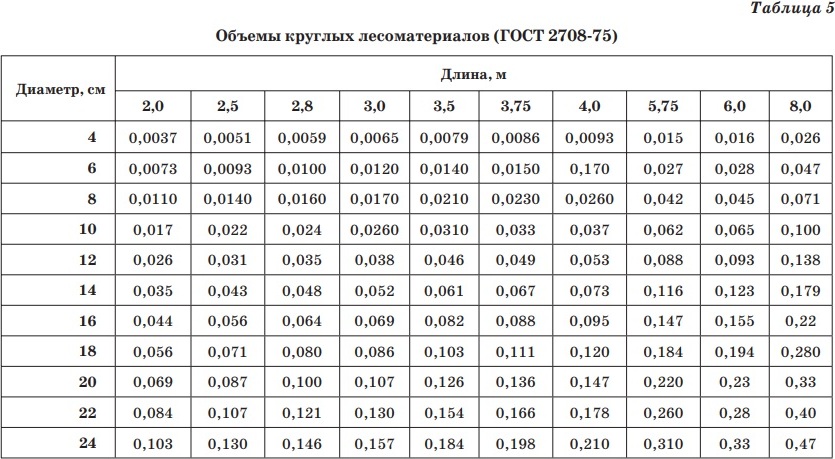 , например, [7] ):

где L⊥={→k∈Zd:→k⋅→z=0(modn)} — обратная решетка.

3 Реализация

3.1 Вегас

Vegas — это классический алгоритм Лепажа Монте-Карло [8] . Оно использует
выборка по важности для уменьшения дисперсии, для которой итеративно
строит кусочно-постоянную весовую функцию, представленную на
прямоугольная сетка. Каждая итерация состоит из шага выборки, за которым следует
путем измельчения сетки.

В реализации Кубы Вегас может запоминать свою сетку для последующего
вызовы, и он может периодически сохранять свое внутреннее состояние, так что
расчет может быть возобновлен, например. после аварии.

3.2 Вежливый

Внимательный — гибрид Вегаса и Скупца [9] , Монте-Карло.
алгоритм, сочетающий выборку важности в стиле Вегаса с глобальным
адаптивное подразделение.

Алгоритм работы следующий: пока не будет достигнута требуемая точность,
разделить пополам область с наибольшей ошибкой вдоль оси, в которой
флуктуации подынтегральной функции уменьшаются больше всего. Пропорционально количеству
новые образцы в каждой половине для его колебания.

Сетка Вегаса хранится между подразделениями, т. е. регионом, который является
результат n−1 подразделений имел n итераций Вегаса, выполненных на
это. С другой стороны, Suave несколько требователен к памяти, так как ему нужно
сохранить образцы для последующего использования.

3.3 Дивонн

Divonne — это значительно расширенная версия алгоритма CERNlib D151.
[10] . По сути, это алгоритм Монте-Карло, но
Кубатурные правила также встроены для сравнения. Снижение дисперсии
стратифицированная выборка, которой помогают методы численного
оптимизация. Divonne имеет трехфазный алгоритм:

Фаза 1: Разделение

Регион интеграции разбит на субрегионы (приблизительно)
равный спред s, определяемый как

s(r)=Volr2(max→x∈rf(→x)−min→x∈rf(→x)).

(15)

Минимум и максимум каждого субрегиона ищутся с использованием методов из
численная оптимизация (по сути, квазиньютоновский поиск). Затем,
«разделители» перемещаются (см. рисунок), чтобы найти оптимальное
расщепление. Эта последняя процедура может быть искусно переведена в
решение линейной системы и, следовательно, довольно быстро (подробности см.
[10] ).

\SetScale.7
\CBox(5,5)(95,95)СинийПастельСиний
\SetWidth2
\SetColorRed
\Линия(0,20)(100,20)
\Линия(0,65)(100,65)
\Линия(30,0)(30,100)
\Линия(85,0)(85,100)
\SetWidth0
\SetColorBlack
\ДлиннаяСтрелка(1,18)(1,14)
\ДлиннаяСтрелка(1,22)(1,26)
\ДлиннаяСтрелка(1,63)(1,59)
\ДлиннаяСтрелка(1,67)(1,71)
\ДлиннаяСтрелка(28,1)(24,1)
\ДлиннаяСтрелка(32,1)(36,1)
\ДлиннаяСтрелка(83,1)(79,1)
\ДлиннаяСтрелка(87,1)(91,1)

Фаза 2: Отбор проб

Субрегионы, определенные на этапе 1, берутся независимо друг от друга с помощью
одинаковое количество баллов у каждого. Последний экстраполируется из результатов
этапа 1.

Этап 3: уточнение

Регионы, результаты которых на этапах 1 и 2 не совпадают в пределах их
ошибки подразделяются или снова отбираются. Этот этап является дополнением к
исходный алгоритм, так как было обнаружено, что достаточно часто ошибка
оценка, или даже интегральное значение, были отключены, потому что характеристики
подынтегральная функция не была найдена в фазе 1.

В реализацию Cuba добавлены две важные функции:

• .

  Пользователь может указывать экстремумы для сложных подынтегральных выражений.

• Для подынтегральных выражений, выборка которых невозможна слишком близко к границе,
  может быть задано «безопасное расстояние», в пределах которого значения будут
  экстраполируется из двух внутренних точек.

3.4 Кухре

Cuhre — детерминированный алгоритм. Он использует кубатуру Генца – Малика.
правила [3] в глобально адаптивной схеме подразделения.
Алгоритм таков: пока не будет достигнута требуемая точность, разделите пополам
область с наибольшей ошибкой по оси с наибольшей четвертой
разница.

Cuhre был повторно реализован на Кубе в основном для последовательного
интерфейс, он такой же, как исходная подпрограмма DCUHRE
[11] .

4 Сравнение

Сбалансированное сравнение алгоритмов интеграции почти
безнадежный. Производительность сильно зависит от подынтегральной функции, и есть
всегда случаи, и не только академические, в которых одна рутинная
превосходит другие, или наоборот, в котором одна процедура просто дает
неправильные результаты. Это, конечно, главная причина, по которой существует четыре
независимые и легко взаимозаменяемые алгоритмы в библиотеке Cuba.

В этом контексте следует отметить, что статистическая ошибка
оценка, приведенная алгоритмами Монте-Карло, просто констатирует
интервал одной сигмы, или, другими словами, вероятность того, что центральный
значение, лежащее в данном интервале, составляет (всего) около 68%.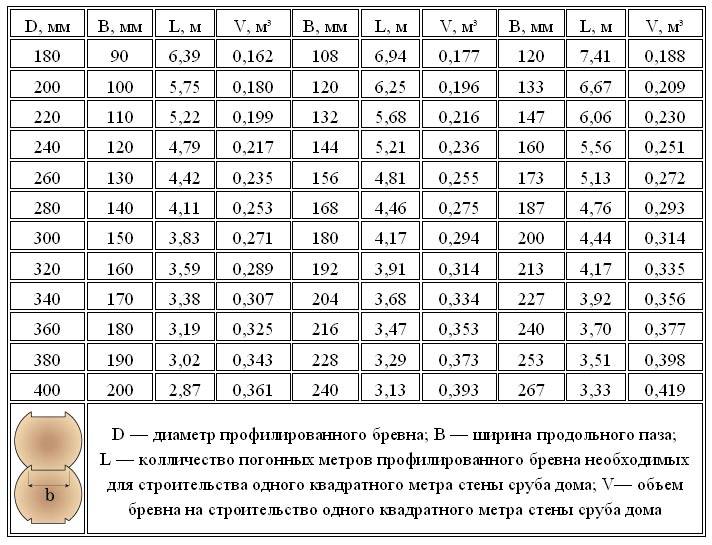

С учетом этих предостережений на следующем графике сравнивается производительность
четыре подпрограммы Кубы на реальной интеграции фазового пространства. Результаты
полученные четырьмя методами (здесь не показаны), действительно согласуются в пределах
запрашиваемая точность.

5 Интерфейс Mathematica

Отдельного упоминания заслуживает интерфейс Mathematica, так как он не
библиотека в прямом смысле. Это скорее четыре исполняемых файла, которые
общаться с Mathematica через MathLink API:

\SetScale.75
\Text(50,85)[b]Математика
\CBox(0,0)(100,80)КрасныйПастельКрасный
\Text(50,65)[]\BlackVegas[f, …]\Text(50,30)[]\Blackintegrand f\Text(50,15)[]\Black(скомпилированная функция)\SetOffset(135,0)
\Текст(50,85)[b]С
\CBox(0,0)(100,80)СинийПастельСиний
\Text(50,65)[]\Blackvoid Vegas(…)\Text(50,25)[]\Образцы Blackrequest\SetOffset(105,0)
\SetWidth2.5
\ДлиннаяСтрелка(-36,65)(36,65)
\Text(0,71)[b]MathLink\Text(0,34)[b]{→x1,→x2,…}\LongArrow(36,30)(-36,30)
\ДлиннаяСтрелка(-36,20)(36,20)
\Text(0,16)[t]{f1,f2,…}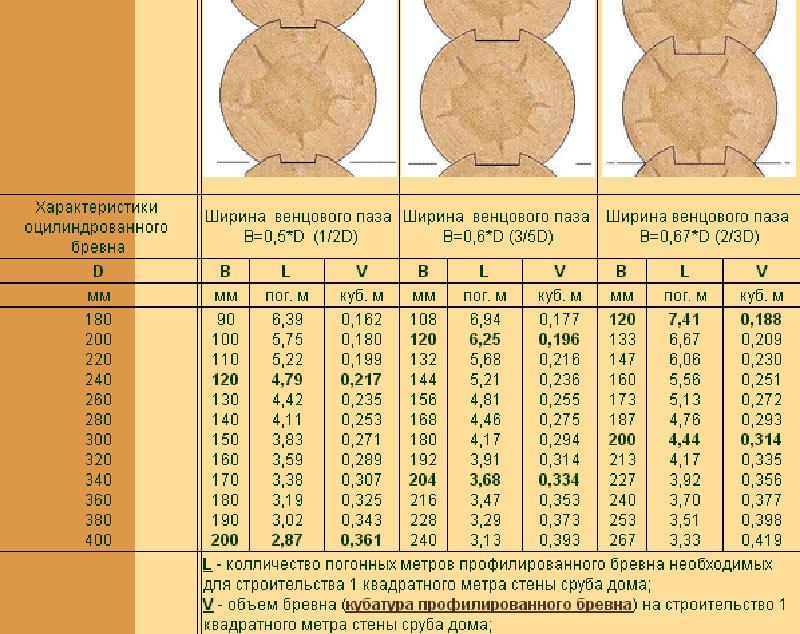

После загрузки соответствующего исполняемого файла MathLink, например. с
Install[«Vegas»], соответствующую процедуру можно использовать практически
как родной NIntegrate для Mathematica. Подынтегральная функция
полностью оценивается в Mathematica, что означает, что можно делать вещи
как

 Cuhre[Zeta[x y], {x,2,3}, {y,4,5}]
 

6 Дополнительные инструменты

6.1 Селектор

Куба включает «универсальный интерфейс», который еще больше упрощает
вызов:

 подпрограмма Куба(метод, ndim, ncomp,
    подынтегральная функция, интеграл, ошибка, проба)
 

Пользователь просто должен выбрать метод = 1,2,3,4 для переключения между
Вегас, Суаве, Дивонн, Кюре. Все параметры индивидуальны
подпрограммы «скрыты» (определены внутри подпрограммы), т. е. это не
готовый продукт, но должен быть адаптирован пользователем.

6.2 Средство просмотра разделов

Средство просмотра разделов Cuba отображает раздел, занятый интеграцией
алгоритм. Иногда это полезно для визуализации того, где подынтегральная функция
лежат характерные области. Это действительно полезно только в малом
умеренные габариты однако.

Уровень детализации 3 должен быть выбран в подпрограмме интеграции и
вывод передается через утилиту partview, например

 myprogram | часть 1 2
 

, который затем отобразит 1–2 плоскость разбиения.
На рис. 2 показан снимок экрана.

Рисунок 2: Скриншот программы просмотра разделов Кубы.

7 Резюме

Cuba – библиотека для многомерного численного интегрирования, написанная
в C. Он содержит четыре независимых алгоритма: Vegas, Suave, Divonne,
и Cuhre, которые имеют аналогичные заклинания и могут быть легко заменены на
сравнение. Все подпрограммы могут интегрировать векторные интегралы и иметь
Интерфейс Fortran, C/C++ и Mathematica. Дополнительные инструменты
включены, такие как универсальный вызов и средство просмотра разделов. Куба
доступен на http://www.feynarts.de/cuba под лицензией
LGPL и прост в сборке (autoconf).

Каталожные номера

• [1]
• [2]

  Т. Хан, комп. физ. коммун. 168 (2005) 78 [hep-ph/0404043].

• [3]

  А. Генц, А. Малик, SIAM J. Numer. Анальный. 20 (1983) 580.

• [4]
  В.Х. Пресс, С.А. Теукольский, В.Т. Феттерлинг, Б.П. Фланнери, Числовой
  рецепты на Фортране, 2-е издание, Cambridge University Press,
  1992.
• [5]

  П. Братли, Б.Л. Фокс, ACM Trans. Мат. Программное обеспечение 14 (1988) 88.
  Алгоритм ТОМС 659.

• [6]

  М. Мацумото, Т. Нисимура, ACM Trans. Моделирование Комп. Моделирование 8 (1998) 3 и
  http://www.math.sci.hiroshima-u.ac.jp/~m-mat/MT/emt.html.

• [7]

  Х. Л. Кенг, В. Юань, Приложения теории чисел к численному анализу,
  Спрингер-Верлаг, 1981.

• [8]
  Г.П. Лепаж, Ж. Комп. физ. 27 (1978) 192.
  
  Г.П. Лепаж, Отчет CLNS-80/447, Корнельский университет, Итака, Нью-Йорк, 1980.
• [9]

  В.Х. Пресс, Г.Р. Фаррар, Комп. в физ. 4 (1990) 190.

• [10]

  Дж. Х. Фридман, М.Х. Райт, ACM Trans. Мат. Программное обеспечение 7 (1981) 76.
  
  Дж.Х. Фридман, М. Х. Райт, отчет SLAC CGTM-193-РЕВ, ЦГТМ-193, 1981 г.

• [11]

  Дж. Бернтсен, Т. Эспелид, А. Генц, ACM Trans. Мат. Программное обеспечение 17 (1991) 437 и 452.
  Алгоритм ТОМС 698.

Шлем Schuberth R2 Carbon Cubature

Стиль изделия Белый / XS	РевЗилла Артикул № 1564991	МФР. Товар № 4518913360	ДоступностьНет в наличии: введите свой адрес электронной почты ниже, чтобы получить уведомление, когда этот товар появится в наличии.
Стиль продукта Белый / SM	РевЗилла Артикул № 1564992	МФР. Товар № 1325472	ДоступностьНет в наличии: введите свой адрес электронной почты ниже, чтобы получить уведомление, когда этот товар появится в наличии.
Стиль продукта Белый / MD	РевЗилла Артикул № 1564993	МФР.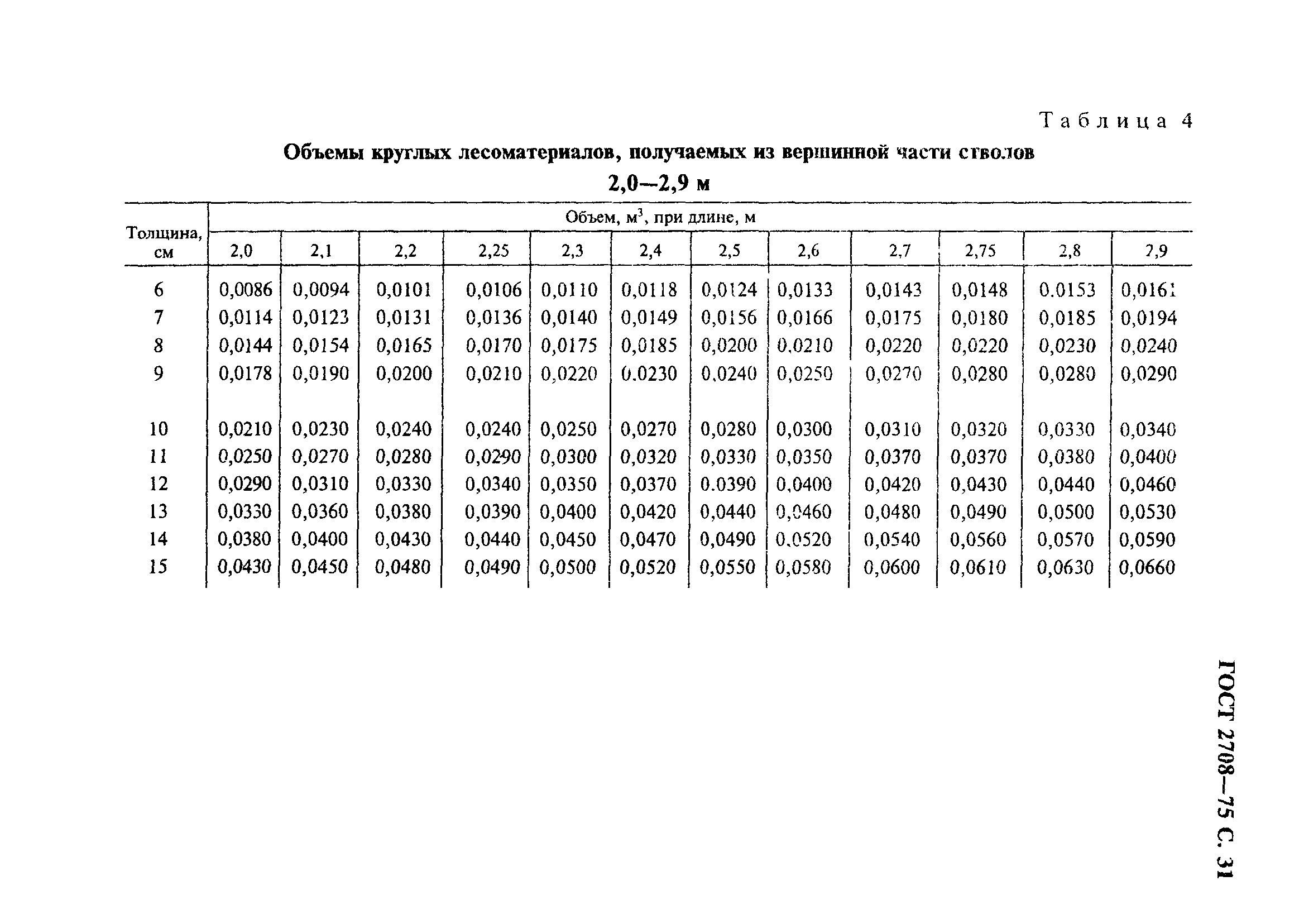 Товар № 1325509	ДоступностьНет в наличии: введите свой адрес электронной почты ниже, чтобы получить уведомление, когда этот товар появится в наличии.
Стиль продукта Белый / LG	РевЗилла Артикул № 1564994	МФР. Товар № 1325549	ДоступностьНет в наличии: введите свой адрес электронной почты ниже, чтобы получить уведомление, когда этот товар появится в наличии.
Стиль изделия Белый / XL	РевЗилла Артикул № 1564995	МФР. Товар № 1325442	ДоступностьНет в наличии: введите свой адрес электронной почты ниже, чтобы получить уведомление, когда этот товар появится в наличии.
Стиль изделия Белый / 2XL	РевЗилла Артикул № 1564996	МФР.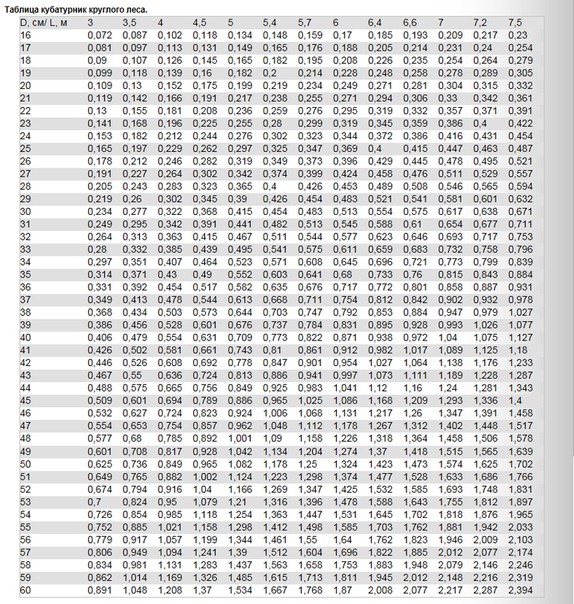 Товар № 1325514	ДоступностьНет в наличии: введите свой адрес электронной почты ниже, чтобы получить уведомление, когда этот товар появится в наличии.
Стиль продукта Желтый / XS	РевЗилла Артикул № 1564997	МФР. Товар № 4518923360	ДоступностьНет в наличии: введите свой адрес электронной почты ниже, чтобы получить уведомление, когда этот товар появится в наличии.
Стиль продукта Желтый / SM	РевЗилла Артикул № 1564998	МФР. Товар № 1325415	ДоступностьОсталось только 1: Доставка в течение 24 часов
Стиль продукта Желтый / MD	РевЗилла Артикул № 1564999	МФР.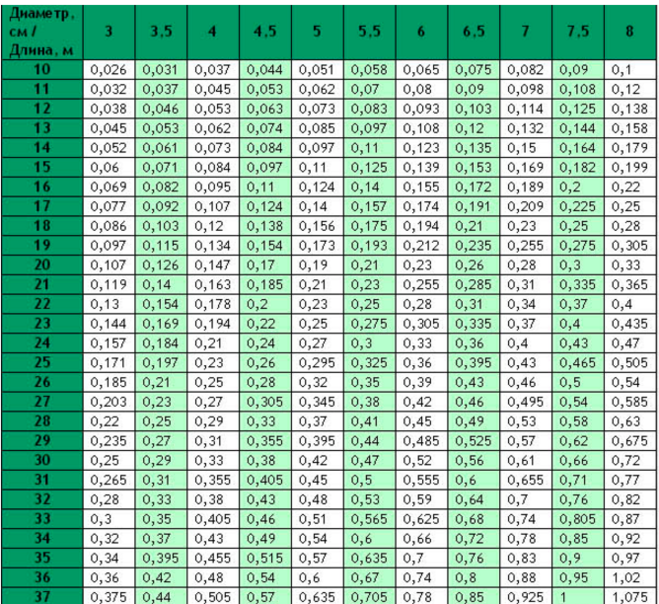 Товар № 1325499	ДоступностьНет в наличии: введите свой адрес электронной почты ниже, чтобы получить уведомление, когда этот товар появится в наличии.
Стиль продукта Желтый / LG	РевЗилла Артикул № 1565000	МФР. Товар № 1325502	ДоступностьНет в наличии: введите свой адрес электронной почты ниже, чтобы получить уведомление, когда этот товар появится в наличии.
Стиль продукта Желтый / XL	РевЗилла Артикул № 1565001	МФР. Товар №1325440	ДоступностьНет в наличии: введите свой адрес электронной почты ниже, чтобы получить уведомление, когда этот товар появится в наличии.
Стиль продукта Желтый / 2XL	РевЗилла Артикул № 1565002	МФР. ← Previous Next → Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сайт