Углы в пространстве — Умскул Учебник
На этой странице вы узнаете
- Как мы сталкиваемся с двугранными углами, когда читаем книгу?
- Где в комнате можно найти перпендикулярные плоскости?
- Как с помощью линейки и листа воспроизвести в жизни теорему о трех перпендикулярах?
Стереометрия — это не просто раздел математики, который нужно долго и нудно учить. На самом деле стереометрия описывает всю нашу жизнь. Стало интересно? Давайте разбираться.
Углы между плоскостями
Мы точно знаем, что угол между стеной и полом равен 90°. Также, как и угол между стеной и потолком, или полом и любым предметом мебели.
Но чему равен угол между двумя открытыми страницами тетради? Или угол между стеной и полуоткрытой дверью? Угол между перилами и плоскостью пола? Все эти углы достаточно легко найти. И ответы на все эти вопросы нам дает именно стереометрия.
Начнем разбирать в углах между плоскостями с того, что введем понятие двугранного угла.
Двугранный угол — это часть пространства, заключенная между двумя полуплоскостями, имеющими общую границу.
Если мы откроем книгу не полностью и посмотрим на пространство между двумя страницами, это пространство и будет двугранным углом.
На рисунке:
АВ — общая прямая для плоскостей, ее называют ребром двугранного угла;
a, b — плоскости, которые образуют двугранный угол, они называются гранями двугранного угла.
| Как мы сталкиваемся с двугранными углами, когда читаем книгу? Если раскрыть книгу не полностью, то ее страницы будут образовывать двугранный угол, то есть часть пространства, заключенную между двумя страницами. |
Заметим, что при пересечении двух плоскостей обычно образуется четыре двугранных угла. Нас интересует меньший из них.
Настало время ввести понятие угла между двумя плоскостями. Но для этого нам нужно провести перпендикуляры к ребру двугранного угла в каждой плоскости. Важно, чтобы перпендикуляры пересекались в одной точке.
Но для этого нам нужно провести перпендикуляры к ребру двугранного угла в каждой плоскости. Важно, чтобы перпендикуляры пересекались в одной точке.
Проведенные перпендикуляры образовали четыре угла. Меньший из них и будет называться углом между плоскостями.
Угол между плоскостями — это угол между перпендикулярами, проведенными к линии пересечения плоскостей. Перпендикуляры должны лежать в данных плоскостях.
Обозначим нужный нам угол на рисунке как угол COD. Он и будет являться углом между данными плоскостями.
Угол COD также будет называться линейным углом двугранного угла.
Линейный угол двугранного угла показывает градусную меру двугранного угла. Поскольку двугранный угол — это часть пространства, то в этом пространстве можно провести множество линейных углов, которые будут равны между собой.
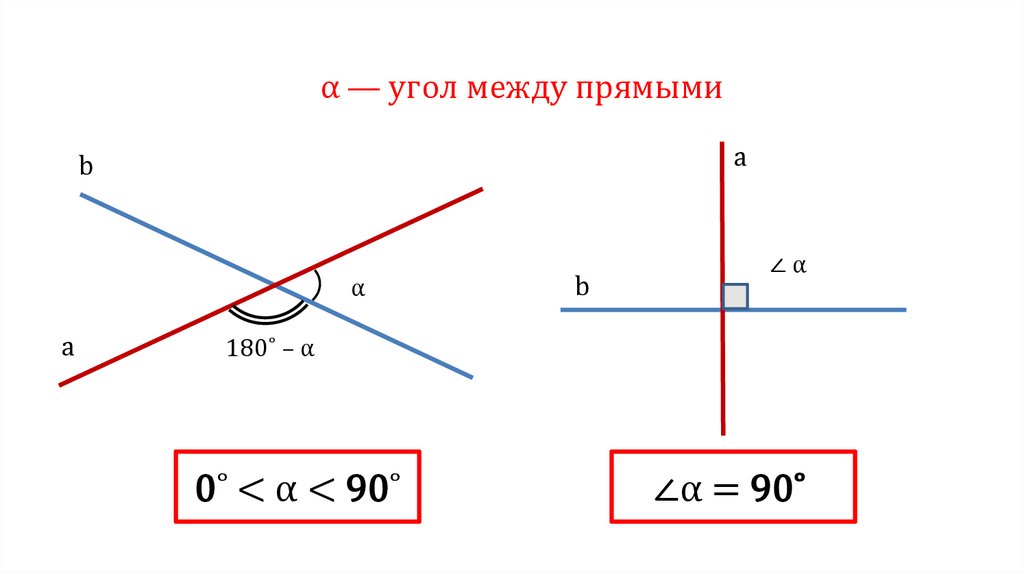
Как и обычные углы, углы между плоскостями бывают трех видов:
- Острые, то есть меньше 900
- Прямые, равные 900
- Тупые, которые больше 90и меньше 1800
Как уже было сказано выше, за угол между плоскостями всегда принимается острый угол, образованный этими плоскостями.
А что будет, если между плоскостями получится прямой угол?
Такие плоскости называются перпендикулярными.
| Где в комнате можно найти перпендикулярные плоскости? Достаточно посмотреть на стены и пол, или стены и потолок. А еще на углы потолка — в них будет три перпендикулярные плоскости. |
У перпендикулярных плоскостей есть одна очень интересная особенность: все углы, образованные ими, равны между собой и равняются 90° градусам.
Чтобы найти угол между плоскостями, необходимо следовать следующему алгоритму.
| Алгоритм нахождения угла между плоскостями 1 шаг. Найти линию пересечения плоскостей. 2 шаг. Достроить к этой линии перпендикуляр в каждой плоскости. 3 шаг. Найти острый угол между построенными перпендикулярами. |
Углы между прямой и плоскостью
Если нарисовать две прямые на листе бумаги, мы с легкостью можем измерить угол между ними с помощью транспортира. А если провести прямую к плоскости, как точно измерить угол между ними?
А если провести прямую к плоскости, как точно измерить угол между ними?
И в этом вопросе к нам снова на помощь приходит стереометрия. Но для начала рассмотрим, что такое угол между прямой и плоскостью.
Угол между прямой и плоскостью — это угол между прямой и ее проекцией на эту плоскость.
Что такое проекция? Предположим, мы проткнем лист бумаги (плоскость) очень длинной иглой.
А теперь сделаем этот рисунок ближе к чертежу. Пусть плоскость а пересекает прямая а в точке О.
Начнем строить проекцию. Прежде чем разобраться, что такое проекция прямой на плоскость, найдем проекцию точки на плоскость.
Возьмем на нашей прямой а точку А и опустим из нее перпендикуляр к плоскости а. Точка, в которой перпендикуляр пересечет плоскость, будет называться проекцией точки на плоскость. На рисунке обозначим ее как А1.
Проекция точки на плоскость — это основание перпендикуляра, опущенного из этой точки на плоскость.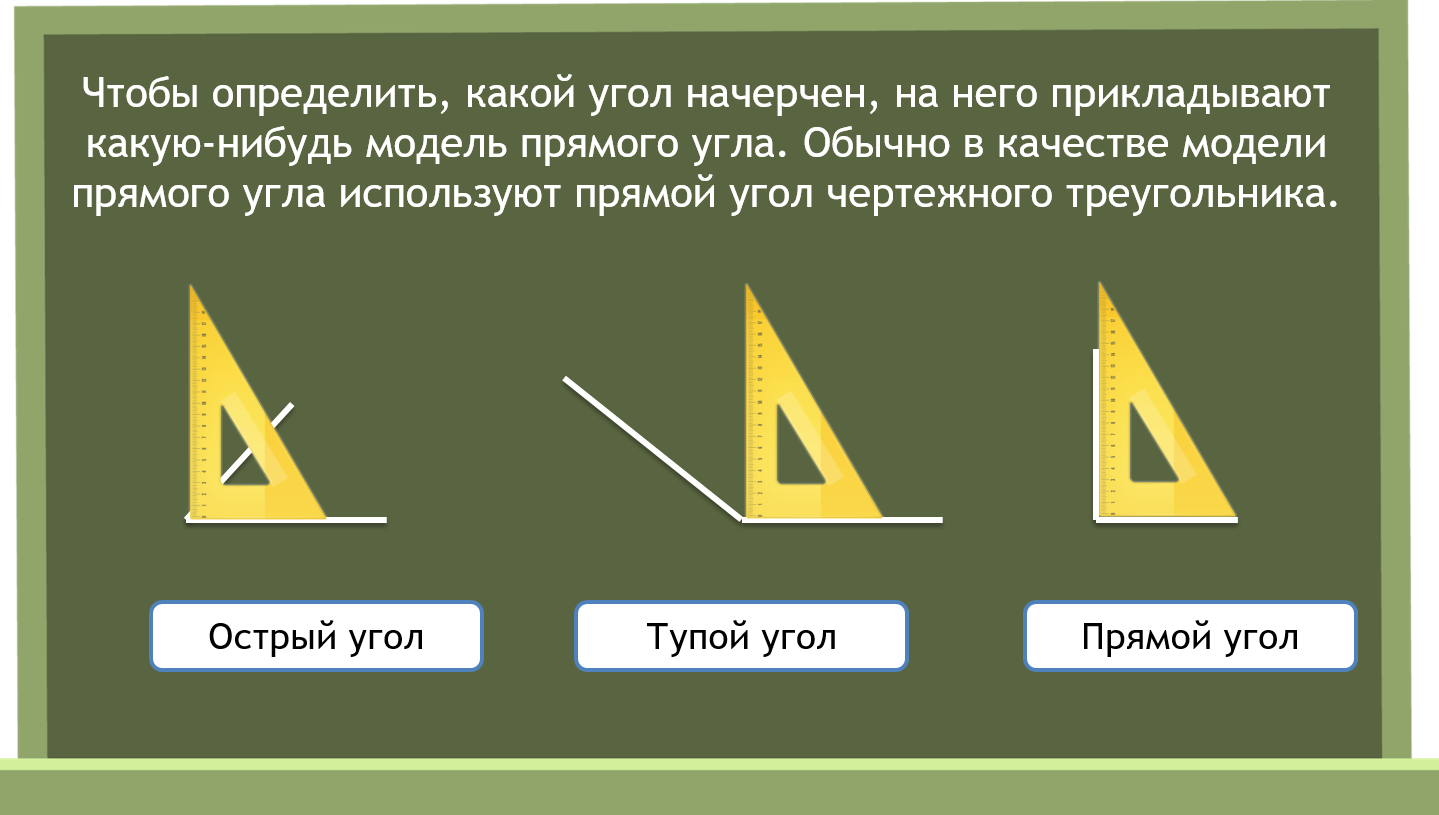
Теперь, если мы будем брать каждую точку на прямой и проектировать ее на плоскость а, то получим проекцию этой прямой на плоскость. Но поскольку на прямой бесконечное множество точек, достаточно соединить точки А1 и О, получаем, что А1О — проекция прямой а на плоскость а.
Заметим, что если мы проведем из любой точки прямой проекцию к плоскости, то попадем на прямую А1О.
Проекция прямой а на плоскость — это прямая а1, образованная проекциями всех точек прямой а на плоскость.
Таким образом можно построить проекции не только прямой, но и любой фигуры.
Мы построили угол из определения. Тогда углом между прямой а и плоскость а будет угол А1ОА.
В этом случае мы также берем острый угол, образованный прямой и плоскостью.
| Алгоритм нахождения угла между прямой и плоскостью Шаг 1. Шаг 2. Найти угол между прямой и построенной проекцией. |
Если прямая параллельна плоскости угол будет равен 0.
Проекция прямой на плоскость будет этой же прямой, просто лежащей в плоскости.
Когда прямая перпендикулярна плоскости, проекцией прямой на плоскость будет точка пересечения прямой и плоскости. Угол между прямой и плоскостью будет равен 90°.
Чуть подробнее остановимся на случае, когда прямая перпендикулярна плоскости.
Прямая, перпендикулярная плоскости — прямая, которая перпендикулярна к каждой прямой, лежащей в этой плоскости.
А что делать, если прямая будет перпендикулярна только одной прямой из плоскости? По определению обязательно, чтобы она была перпендикулярна всем прямым из плоскости. Как тогда проверить перпендикулярность?
Для этого существует признак перпендикулярности прямой и плоскости:
- Если прямая перпендикулярна к двум пересекающимся прямым в этой плоскости, то она будет перпендикулярна этой плоскости.

Следовательно, если необходимо в задаче доказать перпендикулярность прямой и плоскости, достаточно доказать, что прямая будет перпендикулярна всего двум пересекающимся прямым в этой плоскости, а не всему множеству прямых, лежащий в данной плоскости.
Рассмотрим несколько интересных свойств, связанных с прямой, перпендикулярной к плоскости.
Свойство 1. Через любую точку пространства можно провести единственную прямую, перпендикулярную плоскости.
Попробуйте подставить уголок к стене из любой точки. Получится ли у вас сделать так, что из одной и той же точки уголок встанет перпендикулярно стене несколько раз? Нет.
Свойство 2. Если две прямые перпендикулярны одной и той же плоскости, то такие прямые параллельны.
Здесь тоже просто все доказать. Достаточно построить в плоскости прямую, которая пересечет две данные прямые и посмотреть на рисунок “сбоку”. Заметим, что соответственные углы равны, а значит, прямые параллельны.
Подробнее про соответственные углы и параллельные прямые можно прочитать в статье “Основы планиметрии”.
Свойство 3. Если к одной прямой перпендикулярны две плоскости, то такие плоскости параллельны.
Тут такие же рассуждения, как и в предыдущем свойстве: достаточно построить прямые, принадлежащие плоскостям, и посмотреть на них “сбоку”.
Свойство 4. Если через перпендикулярную к плоскости прямую проходит плоскость, то данные плоскости будут перпендикулярны.
Это легко проверить, если найти любой двугранный угол между построенными плоскостями.
Теорема о трех перпендикулярах
Разберем еще одну очень интересную теорему, связанную с проекциями прямой на плоскость. А именно мы рассмотрим теорему о трех перпендикулярах.
Для начала попробуем понять ее на реальных предметах.
Как с помощью линейки и листа воспроизвести в жизни теорему о трех перпендикулярах?
Возьмем уголок и зафиксируем его строго вертикально на листе.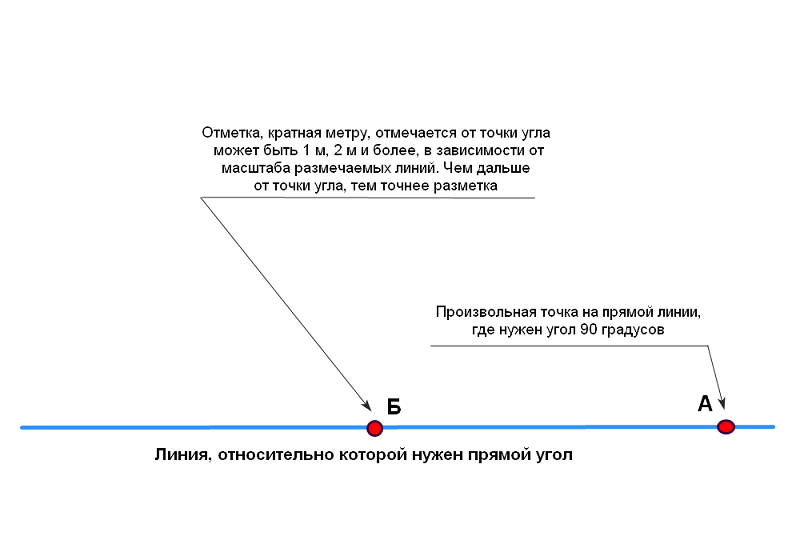 Для удобства назовем уголок АВС, где С — прямой угол.
Для удобства назовем уголок АВС, где С — прямой угол.
Сразу заметим, что прямая АС будет перпендикулярна плоскости листа (поскольку уголок стоит строго вертикально, а лист лежит строго горизонтально).
Дальше заметим, что прямые АС и ВС также перпендикулярны, поскольку в уголке угол С равен 90°.
Посмотрим чуть-чуть внимательнее и обратим внимание, что прямая ВС при этом будет проекцией на плоскость листа прямой АВ.
Немного достроим наш рисунок и через точку В проведем прямую, перпендикулярную ВС. Назовем эту прямую КМ.
Сразу отмечаем, что прямая КМ перпендикулярна ВС по построению, а также перпендикулярна прямой АС (поскольку АС — перпендикуляр к плоскости листа).
Можем ли мы что-то еще сказать про нашу ситуацию? Оказывается, прямая АВ также будет перпендикулярна прямой КМ.
Возникнет вопрос, почему?
1. Вспомним признак перпендикулярности прямой и плоскости: если прямая перпендикулярна к двум пересекающимся прямым в этой плоскости, то она будет перпендикулярна этой плоскости.
Теперь узнаем, как этот признак выполняется в данной ситуации.
2. Посмотрим на ситуацию немного под другим углом и в этот раз возьмем за плоскость не лист, а нашу линейку.
3. Тогда две пересекающиеся прямые в плоскости линейки будут перпендикулярны прямой КМ: BCKM по построению, а ACKM как прямая, перпендикулярная к плоскости листа, а значит, и перпендикулярная всем прямым в этой плоскости.
4. Получается, что прямая КМ перпендикулярна плоскости АВС, следовательно, перпендикулярна и всем прямым в этой плоскости, в том числе прямой АВ.
Таким образом, длинная сторона линейки будет наклонной прямой, основание — ее проекцией, а начерченная линия — перпендикуляром к проекции.
Мы рассмотрели теорему о трех перпендикулярах. Осталось ее только сформулировать математическим языком.
Теорема о трех перпендикулярах
Если наклонная прямая АВ к плоскости а перпендикулярна прямой КМ в этой плоскости, то и проекция прямой АВ на плоскость а перпендикулярна к прямой КМ.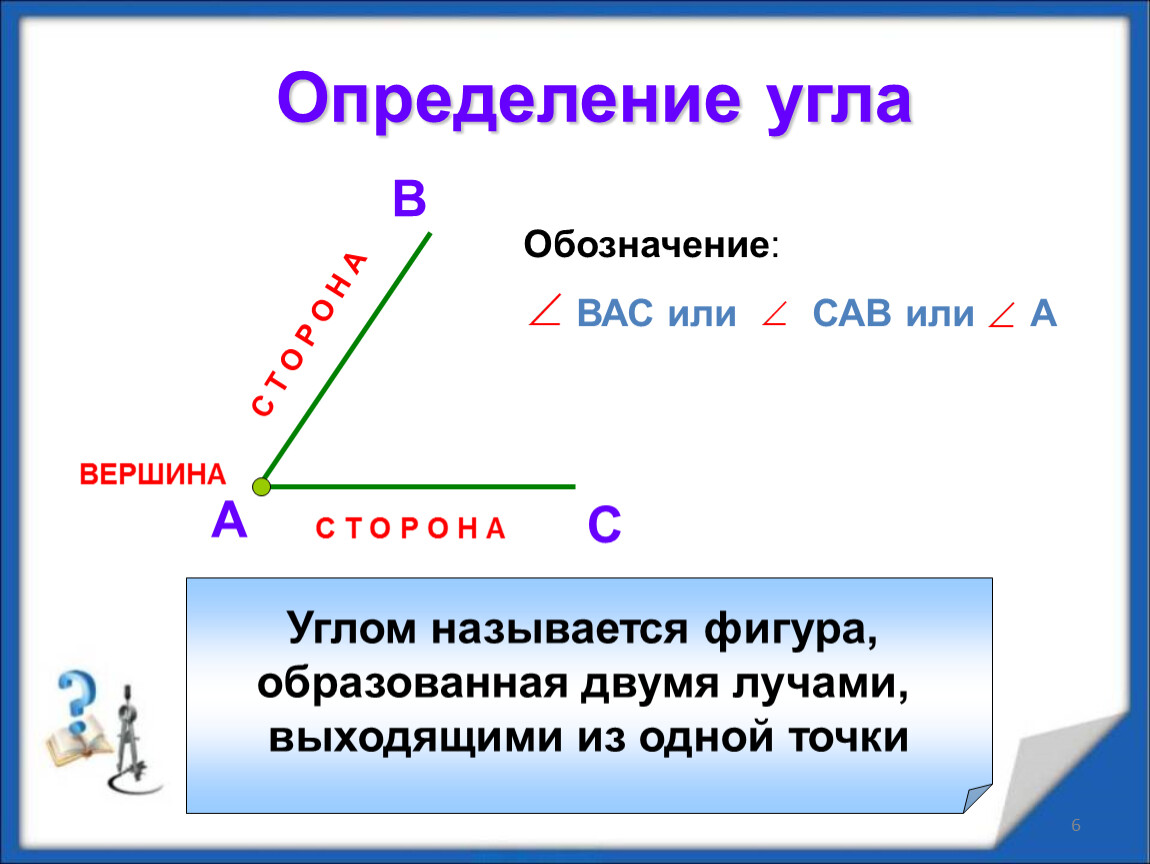
Для построения чертежа заменим линейку на несколько отрезков. Тогда АВ — наклонная, ВС — проекция, КМ — прямая в плоскости.
| Как с помощью линейки и листа воспроизвести в жизни теорему о трех перпендикулярах? Для этого нужно взять лист бумаги и треугольную линейку. На листе бумаги построить произвольную прямую, а после поставить линейку строго вертикально так, чтобы основание линейки на листе было перпендикулярно начерченной прямой. Таким образом, длинная сторона линейки будет наклонной прямой, основание — ее проекцией, а начерченная линия — перпендикуляром к проекции. |
Вот и все, ничего сложного. А называется теорема так потому, что в построении действительно присутствуют три перпендикуляра, которые отлично видно на рисунке.
Теорему о трех перпендикулярах можно активно использовать для доказательства и решении задач.
Фактчек
- Двугранный угол — это часть пространства, заключенная между двумя полуплоскостями, имеющими общую границу.
 Градусной мерой двугранного угла будет линейный угол двугранного угла или, другими словами, угол между плоскостями.
Градусной мерой двугранного угла будет линейный угол двугранного угла или, другими словами, угол между плоскостями. - Угол между плоскостями — это угол между перпендикулярами, проведенными к линии пересечения плоскостей. Перпендикуляры должны лежать в данных плоскостях. За угол между плоскостями принимают острый угол, образованный этими плоскостями. Если угол между плоскостями равен 90°, то такие плоскости перпендикулярны.
- Угол между прямой и плоскостью — это угол между прямой и ее проекцией на эту плоскость. Чтобы найти угол между прямой и плоскостью, необходимо построить проекцию прямой на плоскость и найти угол между прямой и ее проекцией. Если прямая параллельна плоскости, то угол между ними будет равен 0°. Если прямая перпендикулярна плоскости, то угол между ними будет равен 90°.
- Прямая, перпендикулярная плоскости — прямая, которая перпендикулярна к каждой прямой, лежащей в этой плоскости. Чтобы доказать, что прямая перпендикулярна плоскости, достаточно доказать, что эта прямая перпендикулярна двум пересекающимся в плоскости прямым.

- Теорема о трех перпендикулярах гласит, что если наклонная прямая а к плоскости а перпендикулярна прямой b в этой плоскости, то и проекция прямой а на плоскость а перпендикулярна к прямой b.
Проверь себя
Задание 1.
Выберите верное утверждение.
- Градусной мерой двугранного угла будет линейный угол двугранного угла. При этом все линейные углы двугранного угла равны между собой;
- Градусной мерой двугранного угла будет линейный угол двугранного угла. При этом линейные углы двугранного угла не равны между собой;
- Грань двугранного угла — это общая прямая плоскостей, которые его образуют;
- Ребра двугранного угла — это плоскости, которые его образуют.
Задание 2.
Угол между плоскостями — это…
- Тупой угол между перпендикулярами, проведенными к линии пересечения плоскостей;
- Острый или прямой угол между перпендикулярами, проведенными к линии пересечения плоскостей;
- Тупой угол между двумя произвольными линиями, проведенными к линии пересечения плоскостей;
- Острый или прямой угол между двумя произвольными линиями, проведенными к линии пересечения плоскостей.

Задание 3.
Что такое проекция прямой на плоскость?
- Это любая прямая, проведенная из точки пересечения прямой и плоскости;
- Это перпендикуляр, опущенный из любой точки на плоскость;
- Это всегда точка пересечения прямой и плоскости;
- Это прямая, образованная проекциями всех точек прямой на плоскость.
Задание 4.
Какой будет проекция прямой, перпендикулярной к плоскости, на эту плоскость?
- Проекция будет равна этой прямой и параллельна ей;
- Проекция будет меньше прямой и образовывать с ней угол;
- Проекция будет точкой пересечения прямой и плоскости;
- Проекция будет больше прямой и образовывать с ней угол.
Задание 5.
Как доказать, что прямая перпендикулярна плоскости?
- Достаточно доказать, что прямая перпендикулярна одной любой прямой в плоскости;
- Достаточно доказать, что прямая перпендикулярна двум параллельным прямым в плоскости;
- Достаточно доказать, что угол между прямой и любой прямой в плоскости равен 90°;
- Достаточно доказать, что прямая перпендикулярна к двум пересекающимся прямым в этой плоскости.

Ответы: 1. — 1 2. — 2 3. — 4 4. — 3 5. — 4
Этап | Образовательная цель этапа урока | Формы, методы и приемы | Деятельность учителя | Деятельность обучающегося | Планируемые результаты | Дидактические и интерактивные средства |
Самоопределение к деятельности | Включение в учебную деятельность на личностно значимом уровне | Форма (Ф ) Словесный: слово учителя |
— Я рада вас приветствовать на нашем уроке . -Ну-ка, проверь, дружок, Готов ли ты начать урок? Все ль на месте? Все ль в порядке? Ручка, книжка и тетрадка? Все ли правильно сидят? Все ль внимательно глядят? Каждый хочет получать Только лишь отметку«5»! — Сегодня мы вновь продолжаем путешествие по стране ГЕОМЕТРИЯ. — Вспомните, кто же является королевой этой страны? — Правильно. Именно она, ТОЧКА, сегодня познакомит нас с новыми геометрическими фигурами. 2. Создание эмоционального настроя. | 1. Показывают готовность к уроку. 2.Приветствуют учителя Точка | Р: выработка учебной мотивации, установление связи между целью учебной деятельности и ее мотивом Л: самоопределение П: целеполагание | Слайд 1 |
Актуализация знаний и мотивация (4-5 мин) | Готовность мышления и осознание потребности к построению нового способа действий Словесный: учебный диалог Практический: выполнение задания «магический квадрат» | Индив. Фронт. Парная работа |
Практическая работа № 1. -Возьмите белый лист формата А-5 — Отметьте на листе бумаги точку О и проведите лучи ОВ и ОА. — На сколько частей лучи разделили плоскость? — Закрасьте меньшую часть цветным карандашом. — Кто знает, какую геометрическую фигуру мы получили? — Чем будет являться точка О? — Сколько вершин у угла? — Покажите цв. карандашом вершину вашего угла. -Чем будут являться лучи ОА и ОВ? — Сколько сторон у угла?
— Какие части мы можем выделить в угле? — Кто может сказать, что же такое угол? — Вы, конечно, знаете, что у каждой геометрической фигуры есть название, и у углов тоже есть название. — Каждый угол имеет своё имя, название. Догадайтесь, как называется этот угол? — Верно – это угол АОВ, или ВОА или угол О. — Записывают это так: — Как образовалось название угла? — Запишем этот знак в тетради. — А теперь потренируемся в записи углов. Слайд 10. А Е D В К D С — Работать будем в парах. Проводит проверку с помощью экрана — Проверим с помощью экрана. — Найдите в классе похожие углы. — Много ли таких углов? — А каких углов больше в нашем классе? — Где в классе мы можем наблюдать прямые углы? — Что значит прямой угол? — Почему у вас разные ответы? — |
на две части Угол Точка О – вершина угла 1 стороны угла 2 Точка – вершина и два луча – стороны, которые выходят из этой точки – вершины. Угол – это геометрическая фигура, образованная двумя лучами, выходящими из одной точки Буква, которая называет вершину, читается в середине. Все буквы заглавные. Назвать и записать угол, его стороны и вершину Нет прямых Потому что это не изучали | П:ориентирование в своей системе знаний П: выстраивание логической цепи рассуждений, доказательств К: точное и полное выражение своих мыслей | |
Постановка учебной задачи | Выявление места и причины затруднения, постановка цели урока | Форма (Ф ) Словесный: учебный диалог Наглядный: демонстрация |
— Сформулируйте тему нашего урока — Начертите на бумаге прямой угол. (А-5) — Какие возникают вопросы? — У кого возникли затруднения? — Как построить угол, если бумага нелинованная? — Как доказать, что построенный вами угол прямой? — Посмотрите на список наших вопросов — Попробуем разобраться вместе. — Как вы думаете, какова цель нашего урока? |
Прямой угол Возникает проблема Вопросы: 1. Как построить прямой угол? 2. Каким инструментом пользоваться? 3. Как определить, что угол прямой? Научиться строить и определять прямой угол | П: подведение под понятие П: целеполагание К: точное и полное выражение своих мыслей П: самостоятельное выделение и формулирование познавательной цели | Слайд 8 |
«Открытие» детьми нового знания | Построение детьми нового способа действий и формирование способности к его выполнению | Форма (Ф,Г,И) Словесный: слово учителя Словесный: учебный диалог Наглядный: демонстрация Практический: работа с учебником, упражнение Практический: выполнение упражнения | Выдает задание. Практическая работа № 3 — Сложите лист бумаги пополам, а потом ещё раз пополам. (А-4) — Разверните модель. — На сколько частей прямые разделили плоскость? — Эти пересекающиеся прямые образовали углы. — Как вы думает, как будут называться углы, которые образовались при пересечении прямых? — Заштрихуйте прямые углы разными цветами. — Мы столкнулись с еще одной проблемой, с тем, что мы пока не знаем. Давайте добавим этот вопрос в наш список вопросов на доске. — Значит, чему мы еще должны научиться сегодня на уроке? — Где мы можем найти ответ на вопр — Как вы поняли, как называются пересекающиеся прямые, которые образуют 4 прямых угла? — Пересекающиеся прямые, образовавшие 4 прямых угла, называются перпендикулярными прямыми. — Ребята, с помощью какого чертежного инструмента удобно строить и проверять прямой угол? — Как он называется? — Прямые углы удобно находить и строить с помощью угольника. — Возьмите угольники. При помощи модели, изготовленной вами путем перегибания бумаги найдите прямой угол. — Сколько прямых углов на угольнике? — Проверьте с помощью модели, два других угла прямые? — Где прямой угол? Наклейте на него красный кружок.
ДИНАМИЧЕСКАЯ ПАУЗА — Я буду показывать вам геометрические фигуры, если в них есть углы, надо сосчитать их и присесть столько раз, если углов нет то 3 хлопка в ладоши. | Выполняют практическую работу Выполняют действия, сказанные учителем На 4 части Они пересекаются 4 прямые углы Вершиной угла Затруднение Узнать, как называются пересекающиеся прямые, которые образуют 4 прямых угла учебник– правило перпендикулярными прямыми Раздаю детям угольники Он один Два других угла непрямые Выполняют физические упражнения. | К: умение с достаточной полнотой и точностью выражать свои мысли П: анализ объектов с целью выделения признаков
П: использование знако-символических средств Р: выполнение пробного учебного действия | Слайд 12 |
Первичное закрепление | Усвоение нового способа действий | Метод (Г ) Словесный: слово учителя Практический: выполнение упражнения |
Практическая работа №5 — А сейчас поработаем в группах. Каждая группа обсуждает свои задания и потом защищает сделанные ими выводы. Группы могут дополнять ответы других. 1 задание (одинаковое для всех групп). – Мы познакомились с новым чертежным инструментом. — Найдите прямые углы с помощью чертёжного угольника в окружающей вас обстановке – на школьном столе. |
Работа в группах (по 6 человек) Алгоритм: Если вторая сторона угла совпала со второй стороной угольника, то это прямой угол. (3) Совместить вершину прямого угла чертёжного угольника и вершину угла. (1) Совместить одну из сторон чертёжного угольника и сторону угла. (2) | К: умение с достаточной полнотой и точностью выражать свои мысли П: анализ объектов с целью выделения признаков П: осознанное и произвольное построение речевого высказывания П: выполнение действий по алгоритму П: осознанное и произвольное построение речевого высказывания | Слайд 18 Слайд 19 |
Самостоятельная работа с самопроверкой | Интериоризация (переход извне внутрь) нового способа действий, индивидуальная рефлексия достижения цели, создание ситуации успеха | Форма (И) Словесный: слово учителя Словесный: учебный диалог Практический: выполнение упражнения |
Путешествие по стране Геометрия сегодня заканчивается, но не подходит к концу. Догадайтесь, какое слово пропущено. Угол – это геометрическая ______________, образованная двумя ___________, выходящими из одной ___________. Лучи, которые образуют угол, называются _______________ угла. Точка, из которой выходят стороны угла, называется ______________ угла. Для того, чтобы построить угол необходимо провести из одной __________ два ___________. Инструмент для определение и построения прямого угла______________________. Проводит проверку с помощью слайда — Проверьте себя с помощью экрана. — Прошу встать тех ребят, которые выполнили задание без ошибок. — Молодцы! | 1.Выполняют самостоятельную работу Фигура,лучами,точки. | П: анализ объектов с целью выделения признаков П: выполнение действий по алгоритму К: умение с достаточной полнотой и точностью выражать свои мысли П: самостоятельное создание способов решения проблем | Слайд 20
|
Включение в систему знаний, повторение (7-8 мин) | Включение «открытия» в систему знаний, повторение и закрепление ранее изученного | Форма (Г) Словесный: слово учителя Словесный: учебный диалог Практический: выполнение упражнений | 1. 2.Дает задание — Какие задачи мы ставили перед собой на уроке? -Что такое угол? углов? | 1.Вспоминают правила работы в группе Научиться строить и определять прямые углы Это меньшая часть плоскости, ограниченная двумя лучами, имеющими общее начало. С прямым углом Перпендикулярные С помощью угольника: совмещали угол и одну из сторон угольника. Потом смотрели, совпадает ли другая сторона угла со стороной угольника. | К: умение с достаточной полнотой и точностью выражать свои мысли П: анализ объектов с целью выделения признаков П: использование знако-символических средств Р: выполнение пробного учебного действия | Слайд 21 |
Рефлексия деятельности (2-3 мин) | Самооценка результатов деятельности, осознание метода построения, границ применения нового знания | Форма (Ф) Словесный: слово учителя Словесный: учебный диалог Практический: выполнение задания | 1. — Оцените свою работу на уроке. А чего не хватает? Вам необходимо выбрать окно (оценить свою работу) и разместить его на стене дома) Синий – сложно, ничего не понял Спасибо за урок! |
все углы в нем прямые и крыша – с прямым углом. окон | Л: самооценка на основе критерия успешности Л: адекватное понимание причин успеха/неуспеха в учебной деятельности К: выражение своих мыслей с достаточной полнотой и точностью | Слайд 24 |
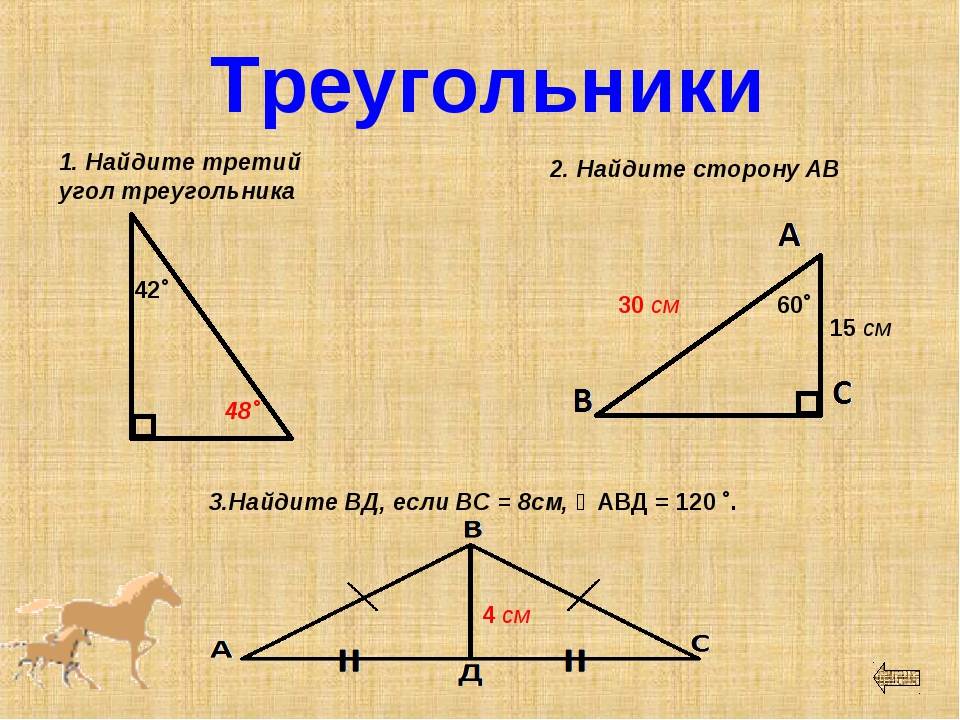
Прямоугольный треугольник
Прямоугольный треугольник — это треугольник, в котором один угол имеет измерение 90° (прямой угол), например треугольник, показанный ниже.
Прямые углы обычно обозначаются квадратом, проведенным в вершине угла, который является прямым углом. Сторона, противолежащая прямому углу прямоугольного треугольника, называется гипотенузой. Стороны, образующие прямой угол, называются катетами. Гипотенуза — самая длинная сторона прямоугольного треугольника.
Так как мера прямого угла равна 90°, а так как сумма трех углов в любом треугольнике равна 180°, сумма двух других углов в прямоугольном треугольнике должна быть 180° — 90° = 90°, поэтому они должны быть острыми углами. В противном случае фигура не может быть треугольником.
Прямоугольные треугольники и теорема Пифагора
Теорема Пифагора, названная в честь греческого математика Пифагора, является одной из наиболее известных теорем в математике. Теорема показывает четкую связь между сторонами прямоугольного треугольника, которая может быть выражена как:
a 2 + b 2 = c 2
где a и b — длины двух катетов, а c — длина гипотенузы прямоугольного треугольника.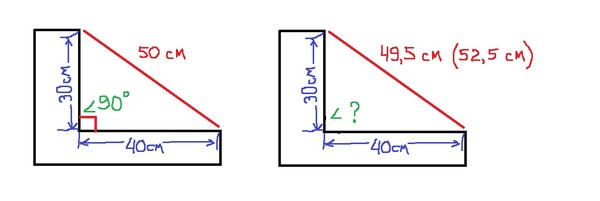
Наборы натуральных чисел, удовлетворяющие уравнению теоремы Пифагора, называются тройками Пифагора. Если у треугольника такие длины сторон, что множество сторон составляет пифагорову тройку, треугольник является прямоугольным. Кроме того, если все длины сторон прямоугольного треугольника являются целыми числами, они представляют собой набор пифагорейских троек.
Например, если a = 3, b = 4 и c = 5, то: Теорема Ифагора выполняется, а 3-4-5 — набор пифагорейских троек.
Существует множество наборов пифагорейских троек. Примеры включают 5-12-13, 6-8-10, 7-24-25, 9-12-15, 9-40-41.
Прямоугольные треугольники в тригонометрии
Прямоугольные треугольники широко используются в тригонометрии. В тригонометрии стороны прямоугольного треугольника часто называют противоположной стороной и прилежащей стороной соответствующего острого угла θ, как показано на рисунке ниже.
Тригонометрические функции часто определяются в терминах прямоугольных треугольников следующим образом:
Вписанный прямоугольный треугольник
Если прямоугольный треугольник вписан в окружность, то одна из его сторон (гипотенуза) является диаметром окружности.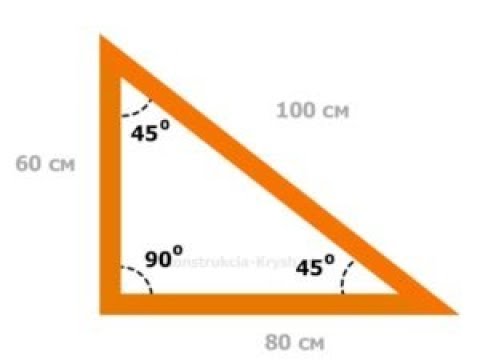 И наоборот, если диаметр окружности образует одну из сторон вписанного треугольника, вписанный треугольник является прямоугольным.
И наоборот, если диаметр окружности образует одну из сторон вписанного треугольника, вписанный треугольник является прямоугольным.
Показанный выше прямоугольный треугольник ABC с гипотенузой AB вписан в окружность O. Дуга в два раза больше угла, на который она опирается в любой точке окружности, поэтому дуга ADB в два раза больше прямого угла ACB.
arc ADB = 2 × 90° = 180°
Центральный угол окружности — это угол, вершина которого находится в центре окружности, а катеты — радиусы, пересекающие окружность в двух различных точках. Мера дуги равна мере центрального угла, опирающегося на нее. Угол AOB является центральным углом описанной выше окружности и пересекает дугу ADB в точках A и B. Исходя из этого, мы знаем, что угол AOB равен 180°, что делает его прямым углом. Любая окружность имеет в общей сложности 360 °, поэтому дуга ADB составляет половину окружности, а это означает, что отрезок AB делит окружность пополам, подтверждая, что гипотенуза прямоугольного треугольника ABC является диаметром окружности.
Прямоугольный треугольник — GCSE Math Steps, Examples & Worksheet
Введение
Как решать задачи на прямоугольные треугольники
Рабочий лист прямоугольного треугольника
Распространенные заблуждения
Практикуйте вопросы по прямоугольному треугольнику
Прямоугольный треугольник GCSE вопросы
Контрольный список обучения
Следующие уроки
Все еще застряли?
Индивидуальные занятия по математике, созданные для успеха KS4
Теперь доступны еженедельные онлайн-уроки повторения математики GCSE
Узнать больше
Введение
Как решать задачи на прямоугольные треугольники
Рабочий лист прямоугольного треугольника
Распространенные заблуждения
Практикуйте вопросы по прямоугольному треугольнику
Прямоугольный треугольник GCSE вопросы
Контрольный список обучения
Следующие уроки
Все еще застряли?
Здесь мы узнаем о прямоугольных треугольниках, в том числе о том, что такое прямоугольный треугольник и как решать задачи, связанные с его сторонами и углами.
Существуют также рабочие листы с прямоугольными треугольниками, основанные на экзаменационных вопросах Edexcel, AQA и OCR, а также дополнительные рекомендации о том, что делать дальше, если вы все еще застряли. 9{\circ} и обозначается квадратиком внутри угла при вершине вместо обычной дуги.
Для решения задач, связанных с прямоугольными треугольниками, нам нужно уметь находить значения других отсутствующих углов или длин сторон и использовать их там, где это необходимо.
Самая длинная сторона прямоугольного треугольника называется гипотенузой . Это сторона, противоположная прямому углу.
Свойства треугольников очень важны в геометрии. Это одна из самых распространенных форм, которую можно распознать на 9.0105 углы в параллельных прямых , теоремы о окружности , внутренние углы , тригонометрия , теорема Пифагора и многие другие. Поэтому вы должны быть знакомы с их индивидуальными свойствами.
Что такое прямоугольный треугольник?
Типы прямоугольных треугольников
Существует два типа прямоугольных треугольников.
- Прямоугольный равнобедренный треугольник
9{\ круг}.
Площадь прямоугольного треугольника
Площадь прямоугольного треугольника можно найти по формуле
A=\frac{1}{2}ч.ч.
, где \text{b} – длина основания 90 105, 90 106, а \text{h} – высота треугольника 90 105, перпендикулярная 90 106. Иногда эти значения необходимо вычислить.
Поскольку треугольник содержит прямой угол, две стороны, прилегающие к прямому углу (не гипотенуза), на перпендикулярны друг другу на , поэтому эти длины можно использовать для вычисления площади треугольника.
Площадь треугольника выражается в квадратных единицах .
Например, чтобы вычислить площадь прямоугольного треугольника ниже, нам нужно знать значение основания \text{b} и значение высоты перпендикуляра \text{h}.
Здесь b=8 и h=6. Это связано с тем, что эти два значения перпендикулярны друг другу, несмотря на то, что основание находится «вверху» изображения.
Значение 10 см может быть обманкой при вычислении площади треугольника, так как это не высота треугольника, а гипотенуза, так что будьте осторожны! 9{2} \конец{выровнено}
Помните, что площадь занимает квадратных единиц .
Пошаговое руководство: Площадь прямоугольного треугольника
Теорема Пифагора
Три стороны прямоугольного треугольника связаны очень полезным свойством, известным как теорема Пифагора.
Теорема Пифагора утверждает, что квадрат наибольшей стороны прямоугольного треугольника (называемой гипотенузой ) равен сумме квадратов двух других сторон. 92.
Сторона c всегда является гипотенузой .
Теорему Пифагора можно использовать для вычисления длины гипотенузы, если мы знаем две другие стороны, и наоборот, мы можем использовать теорему Пифагора для вычисления более короткой стороны, зная гипотенузу и еще одну сторону прямоугольного треугольника. .
.
Подробнее о теореме Пифагора можно узнать здесь.
Пошаговое руководство: Теорема Пифагора
Тригонометрия
Стороны и углы прямоугольных треугольников соединены тригонометрические соотношения синус , косинус и тангенс . Самая длинная сторона до сих пор называется гипотенузой .
Более короткие стороны имеют названия в зависимости от их отношения к углу: напротив и рядом с (рядом с).
Пошаговое руководство: Тригонометрия
Как решать задачи на прямоугольные треугольники
Чтобы решать задачи на прямоугольные треугольники:
- Найдите известные углы, включая прямой угол, и вычислите все необходимые неизвестные углы.
- Найдите известные стороны и рассчитайте все необходимые длины неизвестных сторон.
- Решите задачу, используя любые необходимые значения.

Объясните, как решать задачи на прямоугольные треугольники
Таблица типов треугольников (включая прямоугольный треугольник)
Получите бесплатный рабочий лист прямоугольного треугольника с более чем 20 типами треугольников, вопросами и ответами. Включает рассуждения и прикладные вопросы.
СКАЧАТЬ БЕСПЛАТНО
Икс
Рабочий лист типов треугольников (включая прямоугольный треугольник)
Получите бесплатный рабочий лист с более чем 20 типами треугольников, вопросами и ответами. Включает рассуждения и прикладные вопросы.
СКАЧАТЬ БЕСПЛАТНО
Похожие уроки о треугольниках
Прямоугольный треугольник является частью нашей серии уроков для поддержки пересмотра многоугольников и треугольников . Возможно, вам будет полезно начать с основного урока о треугольниках, чтобы получить краткое изложение того, чего ожидать, или использовать пошаговые руководства ниже для получения более подробной информации по отдельным темам. Другие уроки этой серии включают:
Другие уроки этой серии включают:
- Многоугольники
- Треугольники
- Типы треугольников
- Разносторонний треугольник
- Равнобедренный треугольник
- Равносторонний треугольник 9{\circ}
Пример 4: задача периметра с конгруэнтными прямоугольными треугольниками
Фигура ABC состоит из двух конгруэнтных прямоугольных треугольников, соединенных линией BD . Стороны одного из прямоугольных треугольников равны 5 см, 12 см и 13 см и АС < BD. Вычислите периметр фигуры.
Найдите известные углы, включая прямой угол, и вычислите все необходимые неизвестные углы.
Мы можем добавить прямые углы к диаграмме. Это говорит нам о том, что длина AC перпендикулярна ширине BD. Любые дополнительные углы в форме не нужны, так как мы сосредоточены на периметре, который является длиной.
Найдите известные стороны и рассчитайте все необходимые длины неизвестных сторон.
Нам известно, что длины трех сторон одного из прямоугольных треугольников равны 5 см, 12 см и 13 см.

Поскольку самая длинная сторона треугольника — это гипотенуза, которая является стороной, противоположной прямому углу, мы можем видеть, что AB и BC оба равны 13 см.
Поскольку AC < BD и AC в два раза больше длины AD, AD должно быть равно 5 см, так как тогда AC будет равно 10 см, а BD будет равно 12 см.
Обозначив все эти стороны, мы имеем
Решить задачу, используя любые необходимые значения.
Теперь мы можем определить периметр фигуры.
5+5+13+13=36\text{см}
Периметр фигуры 36\см.
Пример 5: периметр конгруэнтных треугольников
Фигура состоит из двух конгруэнтных прямоугольных треугольников. Стороны треугольника равны 8\см, 15\см и 17\см. Найдите периметр фигуры.
Найдите известные углы, включая прямой угол, и вычислите все необходимые неизвестные углы.
Помните, что есть один прямой угол. Мы можем добавить прямые углы к диаграмме.

Найдите известные стороны и рассчитайте все необходимые длины неизвестных сторон.
Помните, что сторона, противоположная прямому углу, является самой длинной стороной. Самая длинная сторона — гипотенуза. Мы можем добавить стороны прямоугольных треугольников к диаграмме.
Решите задачу, используя любые необходимые значения.
Недостающая сторона – это разница между двумя самыми короткими сторонами 15 см и 8 см.
15-8=7
Периметр можно найти, сложив все стороны фигуры.
17+7+17+8+16=64
Следовательно, периметр равен 64 см.
Пример 6: периметр прямоугольного треугольника
Стороны прямоугольного треугольника относятся как 3:4:5. Периметр 240\см. Вычислите длину гипотенузы.
Найдите известные углы, включая прямой угол, и вычислите все необходимые неизвестные углы.
Не требуется для этого вопроса.
Найдите известные стороны и рассчитайте все необходимые длины неизвестных сторон.

Помните, что сторона, противоположная прямому углу, является самой длинной стороной. Самая длинная сторона — гипотенуза.
Решите задачу, используя любые необходимые значения.
Мы можем разделить периметр на сумму частей отношения. 9{\ круг}.
40 \ см
24 \ см
8 \ см
32 \ см
Мы можем разделить периметр на сумму частей отношения.
96\дел (3+4+5)=8
Затем мы можем умножить 8 на 3, чтобы найти самую короткую сторону прямоугольного треугольника.
3\умножить на 8=24
Самая короткая сторона будет 24 см.
100 \ см
58 \ см
120 \ см
62 \ см
Поскольку мы знаем, что EF, AD и BC имеют одинаковую длину и короче, чем BD и DF, мы можем обозначить каждую из них наименьшей длиной стороны треугольника, 3 \ см .
Поскольку AB, CD, DE и AF являются гипотенузой каждого прямоугольного треугольника, все они могут быть обозначены как длина наибольшей стороны, равная 13 см.

Это означает, что BD и DF равны 12 см. Мы можем добавить к диаграмме размеры прямоугольных треугольников вместе с четырьмя 9углы 0 градусов.
Периметр будет суммой сторон фигуры.
13+13+5+13+13+5=62\текст{см}
98 см
56 см
112 см
108 см
Нам дано, что 2DE < CD . Поскольку DE – длина стороны прямоугольного треугольника, длина DE должна быть равна 7 см, а длина CE должна быть равна 24 см, поскольку 2 × 7<24-7 дает нам 14<17.
Гипотенуза должна быть 25 см, так как это самая длинная сторона. Теперь мы можем добавить к диаграмме размеры прямоугольных треугольников.
Мы можем сложить длины сторон, чтобы найти периметр.
24+7+25+17+25=98\текст{см}
Периметр равен 98\text{см}.
Прямоугольный треугольник Вопросы GCSE
1. Форма A – треугольник.

9{\ круг}
(1)
3. Энергетическая компания разрабатывает новый логотип.
Состоит из четырех равных треугольников со сторонами 6 \ см, \ 8 \ см и 10 \ см.
(a) Запишите порядок осевой симметрии фигуры.
(б) Найдите периметр фигуры.
(4 балла)
Показать ответ
(a) 4
(1)
(б) 8-6=2
(1)
10+2+10+2+10+2+10+2+10+2=4\умножить на 22
(1)
88 \ см
(1)
4. Вот окружность диаметром АВ.
Бонни говорит, что треугольник ABC равносторонний.
Права ли Бонни? Четко объясните свой ответ, указав, к какому типу относится треугольник ABC.
(2 балла)
Показать ответ
Бонни НЕ верна.


 Построить проекцию прямой на плоскость.
Построить проекцию прямой на плоскость.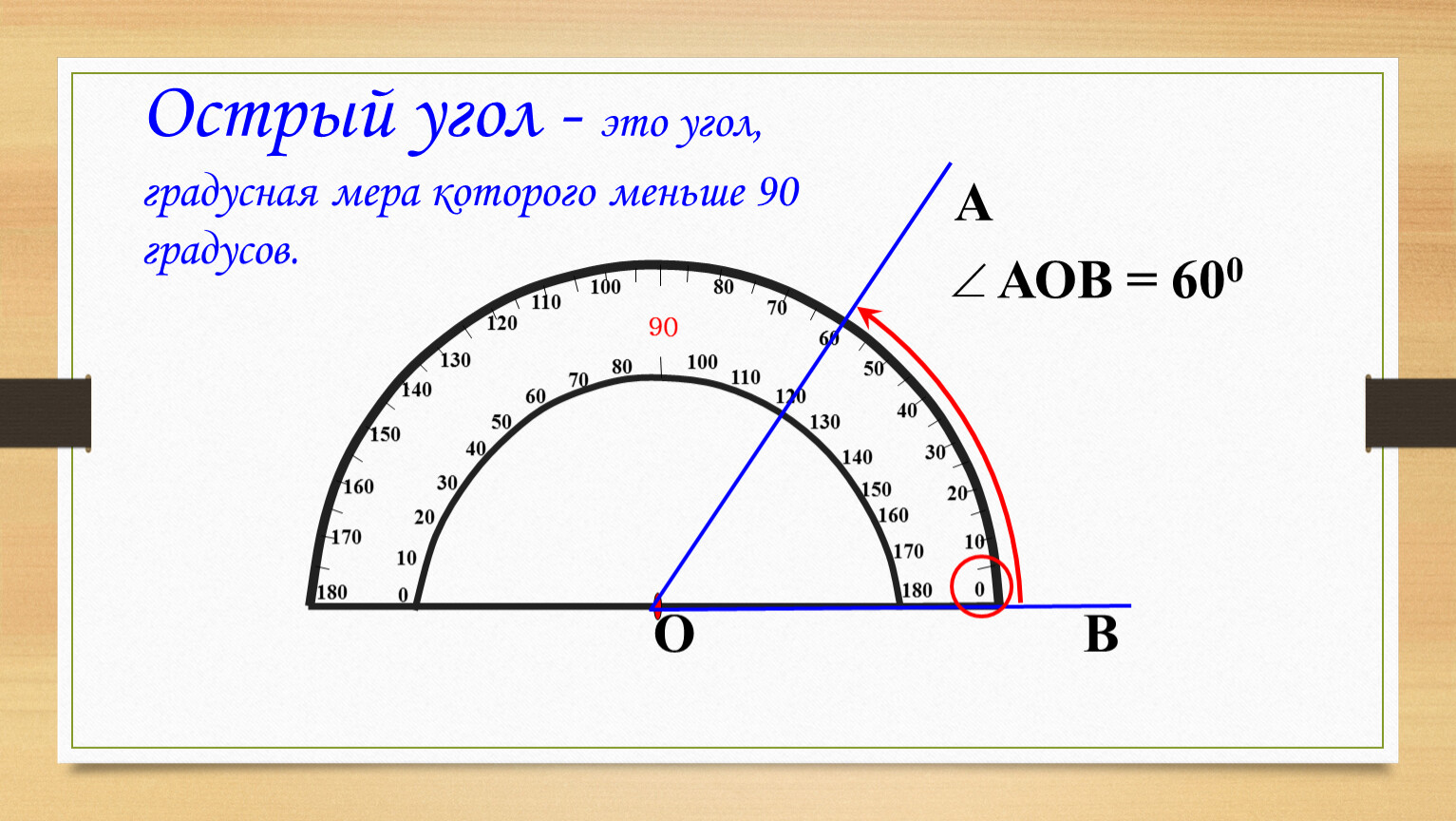
 Градусной мерой двугранного угла будет линейный угол двугранного угла или, другими словами, угол между плоскостями.
Градусной мерой двугранного угла будет линейный угол двугранного угла или, другими словами, угол между плоскостями. 




 Практическая работа
Практическая работа
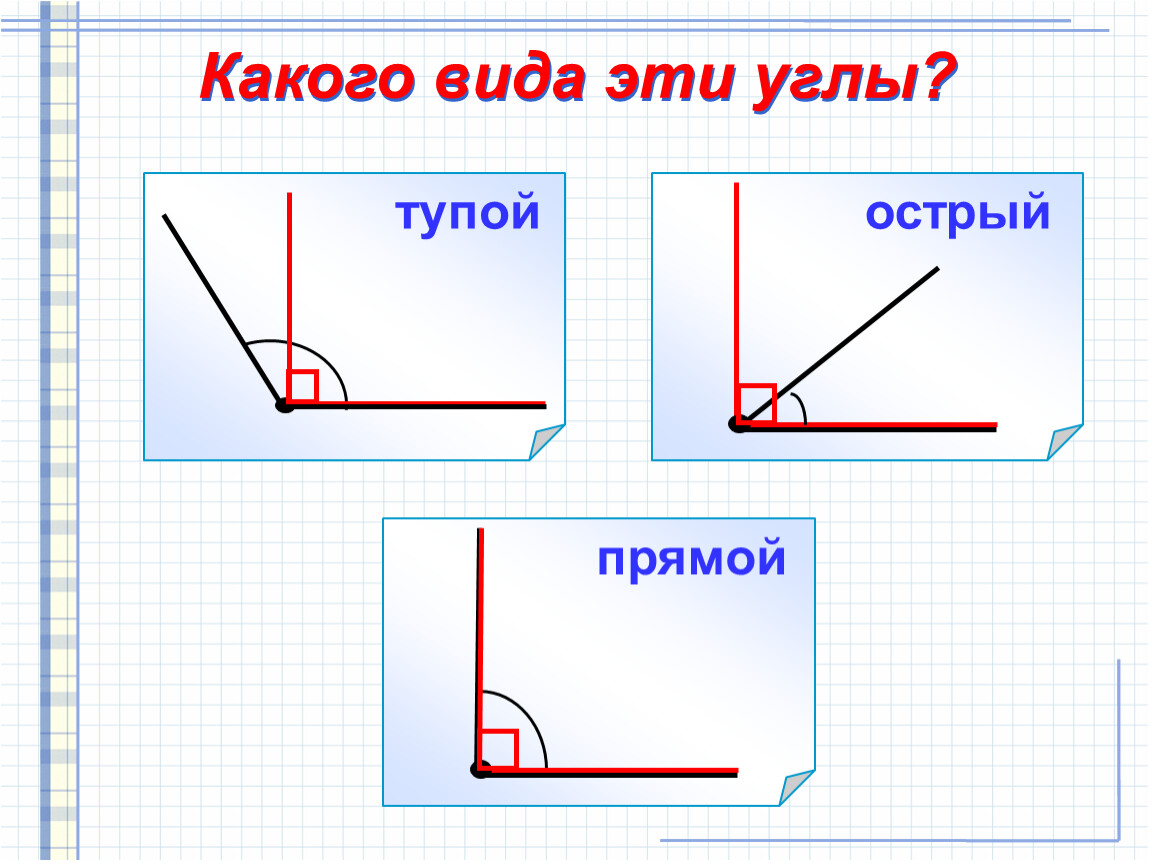
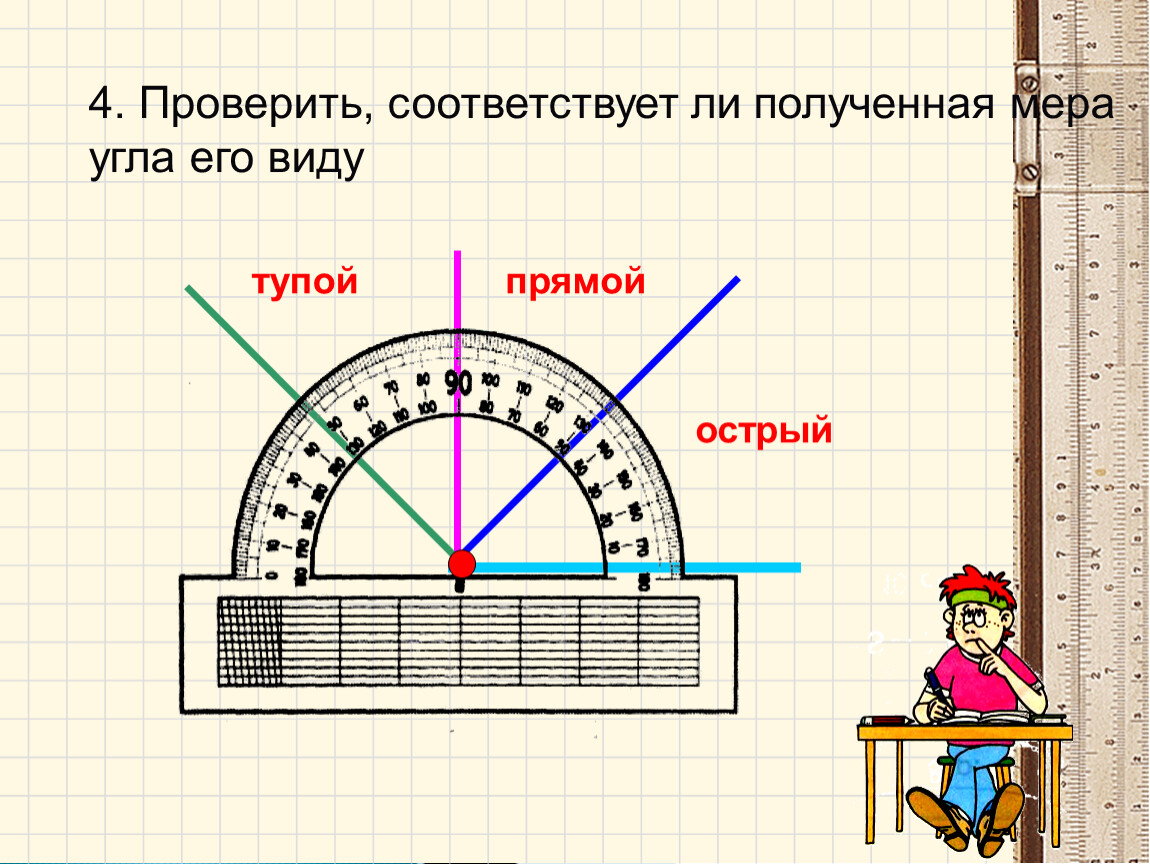
 Подумайте, как при помощи угольника проверить, прямой угол или нет? Составьте в группе алгоритм определения прямого угла – расставьте последовательность операций.
Подумайте, как при помощи угольника проверить, прямой угол или нет? Составьте в группе алгоритм определения прямого угла – расставьте последовательность операций. Мы еще не раз вернемся в эту удивительную страну. А сейчас мы выполним небольшую самостоятельную работу, которая покажет, что мы сегодня узнали на уроке.
Мы еще не раз вернемся в эту удивительную страну. А сейчас мы выполним небольшую самостоятельную работу, которая покажет, что мы сегодня узнали на уроке. Вспоминанают правила
Вспоминанают правила Акцентирует внимание на конечных результатах учебной деятельности обучающихся на уроке.
Акцентирует внимание на конечных результатах учебной деятельности обучающихся на уроке.