Варианты построения прямых углов при строительстве дома и проверка углов при уже возведенном сооружении. — Строю Для Себя
В этой статье хотел бы поделиться, какие вообще распространены варианты построения прямых углов, и как проверить углы уже возведенного дома, не имея доступа к замеру его диагоналей.
Оговорюсь, что вариантов множество, и большинство из них выражается через тригонометрические функции или с помощью сложных геометрических построений))), но нам это ни к чему, так как на стройке никто не будет браться за сложные вещи и сидеть с букварём, теряя время!
В данной статье рассмотрю следующие варианты получения прямого угла:
- теорема Пифагора;
- вариант геометрического построения;
- упрощенный вариант, как производный от геометрического построения.
Теорема Пифагора
Самый часто используемый и очень надежный способ. Теорема устанавливает соотношение между сторонами прямоугольного треугольника: сумма квадратов длин катетов равна квадрату длины гипотенузы.
Можно воспользоваться готовым решением (рисунок ниже) или же зная стороны дома — самому, согласно формулы, произвести расчет «своей» диагонали, и в дальнейшем работать с этим значением.
Основное соотношение сторон треугольника Пифагора — 3, 4 и 5 единиц. Так же для удобства существуют производные треугольники от основного, получаемые, при умножении его сторон на любой коэффициент. К примеру, стороны 3,4,5 умножены на К=2 (коэффициент 2), получаем треугольник со сторонами 6,8,10, и т.д.
Геометрическое построение
Ни чуть не хуже Пифагорова треугольника, но не часто используемое (наверное, в силу забывчивости), хотя очень даже эффективное!
Выглядит страшно, но на деле — проще простого))).
Зная угол здания (точка О), равноудаляем от него две точки О1 и О2 по оси А. Одинаковое расстояние можем откладывать как хотим, используя: рулетку, циркуль (колышек с веревкой) или обрезок доски, да вообще что угодно, главное иметь равные расстояния от точки О.
Из точек О1 и О2 поочередно одинаковым радиусом (радиус произвольный, но больше чем отложенное расстояние от точки О до О1 или О2) чертим дуги примерно там, где будет пересечение их со второй осью В (со второй стеной). Точка пересечения двух дуг (на рисунке дуги выделены зеленым цветом) и будет давать ровно прямой угол с проведенным отрезком к точке О (к углу будущего здания).
Точка пересечения двух дуг (на рисунке дуги выделены зеленым цветом) и будет давать ровно прямой угол с проведенным отрезком к точке О (к углу будущего здания).
Поверьте, этот способ ни чуть не хуже Пифагора, — имея под рукой два колышка и отрезок веревки, делается построение осей будущего дома за 20-40 минут, в зависимости от размера и сложности здания.
И напоследок упрощенный вариант
Вместо черчения дуг от точек О1 и О2, берутся две рулетки (рулетки без погрешности между собой, допустимое отклонение 2-3 мм. на 10 м. по размерной шкале) и кладутся нулевой отметкой к каждой из точек О1 и О2.
Далее просто совмещаем их одинаковыми значениями по мерной шкале (точка Х) и всё, перпендикуляр готов. В данном случае построен равнобедренный треугольник, где его высота делит основание ровно пополам и образует с ним прямой угол.
На практике делается следующим образом: отмечается несколько контрольных точек по двум рулеткам на пересечении делений (к примеру 1 м.
, 3м. и 7м.). Далее по ним протягивается шнур от точки О, и если прямая совпадает со всеми точками — вы сделали правильно, если не совпадает — то перемеряем заново!
Это настолько быстро делается, что на первый взгляд может показаться неправдоподобно, но поверьте — всё это работает со 100% гарантией!
Проверка прямого угла построенного здания
Все вышеописанные способы так же применимы и к уже стоящим зданиям. Они используются как проверка за строителями, а так же в случаях, если требуется заливать фундамент по периметру старого дома и/или ровно облицевать ветхий домик каким-либо материалом.
Всё одинаково, главное вынести размеры за пределы строения, так как внутри — работы уже не реальны.
Используя бечевку, протягиваем ее параллельно стенам и закрепляем колышками. После чего снимаем замер.
При геометрическом построении, пересечение дуг будет не по стене, как выше описывалось, а по «невидимому продолжению стены» (на рисунке обозначено точкой Х).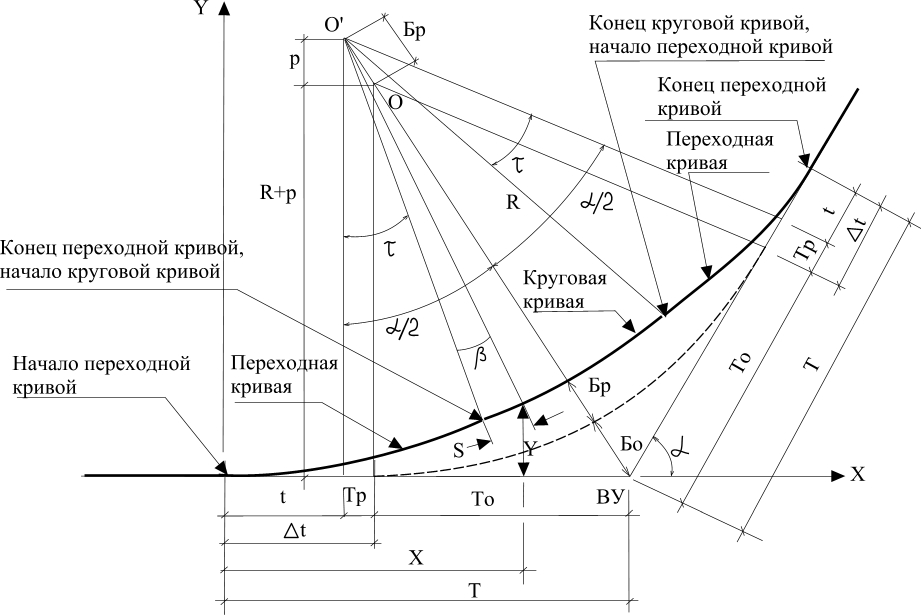 То же самое и с двумя рулетками…
То же самое и с двумя рулетками…
При необходимости, все способы свободно комбинируются или взаимозаменяются.
На этом всё, спасибо Вам за уделенное внимание!
Строительный Калькулятор CI Construction Master 5
Строительный калькулятор CI Construction Master 5 — незаменимый помощник любому профессиональному строителю.
Это простое в использовании устройство для работы в офисе, в производственных условиях гарантирует быстрые и точные математические вычисления в области строительства. Введите необходимые вам числа, и ответ появится незамедлительно благодаря уже встроенным в калькулятор CI Construction Master 5 алгоритмам решения. Он идеально подойдет для разработки планов и схем.
С ним вы сможете сократить риск допущения серьезных ошибок в расчетах расходов и затрат на материалы, сэкономить время и деньги, а также уберечь себя от лишних расстройств!
Где пригодится:
- Вычисление расстояний, площади и объема: конвертация единиц измерений, включая метрическую систему мер.

- Расчеты стропильной конструкции, кровли и каркаса для двух/четырех скатной крыши, подкосов /опорных стоек.
- Расчет лестниц: подступенок, ступени, тетива лестницы, уклон.
- Встроенная функция прямого угла Right-Angle с автоматическим выравниванием.
- Скругленные элементы и арки: площадь, диаметр, окружность.
- Вычисление количество досок, досковых футов.
- Расчет веса на единицу объема.
Калькулятор разработан для подрядчиков, строителей, архитекторов, инженеров и профильных специалистов.
Технические характеристики калькулятора
Размер: 145мм x 76мм x 17мм
Вес изделия: 117.7 г включая крышку и карманное руководство пользователя
Питание: одна 3-х вольтовая долговечная батарея (CR-2016)
Тип дисплея: LCD: 11 цифр (7 обычных, 4 дроби) с индикаторами
Размеры дисплея: 19 мм x 65 мм
Точность: до 10 цифр
Автоматическое отключение экономит заряд батареи.
В комплекте: защитная сдвигающаяся крышка; руководство пользователя на английском; долговечная батарея; гарантия 1 год.
Функции калькулятора
Конвертирует и работает с единицами измерения
Единицы метрической системы (мм, см, м): Есть
Ярды, дробные дюймы, дроби фут-дюйм: Есть
Десятичные футы (10-е, 100-е), дюймы: Есть
Поддержка всех дробных единиц в строительстве: Есть
Конвертация весовой доли: Есть
Работа с правильными углами
Вычисление правильного угла/стропила: Есть
Кнопка нахождения уклона (угол уклона): Есть
Высота, длина, диагональ/стропильная нога: Есть
Угловая стропильная нога/разжелобка, нарожник: Есть
Нестандартная угловая нога/разжелобок, нарожник: Есть
Угол среза стропильной ноги (вертикальный, угловой, ровный): нет
Ступени (осн. и доп.: лимит подступенка, площадка, толщина пола): Основные
Наклонная стена: Есть
Стойки: нахождение межцентрового расстояния: Есть
Вычисление площади и объема
Квадратные и кубические измерения: Есть
Крыша — партии, кв.метры, листы 4х8, уклон, площадь гориз. сечения: нет
сечения: нет
Гипсокартон, сайдинг и панели — 4х8, 4х9, 4х12: нет
Площадь и объем колонны/конуса: нет
Основные и дополнительные вычисления с кругами: Основные
Кнопки длины, ширины, высоты, автоматического расчета площади и объема: нет
Блоки, фундамент: нет
Специальные функции калькулятора
Тригонометрические (синус, косинус, тангенс, арксинус, арккосинус, арктангенс): нет
Борд-футы: Есть
Работа с основными функциями (+, -, х, /, %, π, х2, √х): Есть
Пользовательские настройки: Есть
Кнопка редактирования Backspace: Есть
Стоимость единицы (общая стоимость на основе цены единицы): Есть
Равносторонний многоугольник: нет
Сложные срезы 45о, косые потолочные срезы: нет
Дополнительные возможности и характеристики
Функция Paperless Tape: Есть
Количество ячеек памяти: 4
Математические измерения и конвертация
Конвертирует и работает со следующими строительными единицами измерения: ярды, дробные и десятичные футы и дюймы, а также единицы метрической системы мер — включая вычисление площади и объема с этими единицами.
Находит вес на единицу объема
Встроенные функции калькулятора, позволяющие экономить время
Расчет лестниц — подступенка, ступеней, длины тетивы лестницы и угла наклона; показывает длину и высоту лестницы:
Расчет стропил — стропильной системы, простых и сложных многоскатных крыш, опорных стоек. Также возможен расчет крыш одинакового и неодинакового ската. Отображение межцентрового расстояния стропил;
Расчет скругленных элементов, арок, колонн, опор, окон и так далее;
Функция расчета подкосов и длины распорки при любом межцентровом расстоянии по возрастанию или убыванию;
Расчет лесоматериалов в досках и досковых футах.
Дополнительные функции калькулятора
Пользовательские настройки: установка пользовательских параметров, например, настройки дроби формата 1/2, 1/4, 1/8, 1/16, 1/32, и 1/64;
Кнопка Backspace легко исправит последнее введенное значение;
Быстрое вычисление себестоимость единицы.
Функция «Paperless» Tape позволяет просматривать 20 последних введенных данных для перепроверки вычислений;
Стандартные вычисления
Работает с такими основными математическими действиями как+, -, +/-, x, ÷, %, π, 1/x, x2, и √.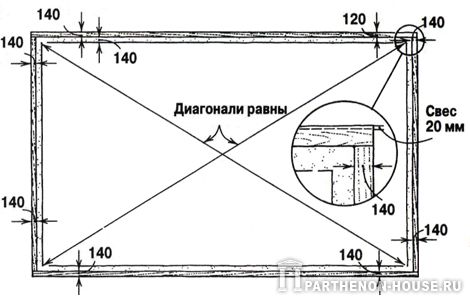
Добавить комментарий
Уведомлять меня о новых комментариях по E-mail
Конструкции прямоугольного треугольника — определение, свойства, построение и примеры решения.
ОБЕЩАНИЕ НА 30 ДНЕЙ | ПОЛУЧИТЕ 100% ВОЗВРАТ ДЕНЕГ*
*T&C Применить
LearnPracticeDownload
Треугольник — это замкнутая фигура, имеющая 3 стороны. Прямоугольный треугольник – это тип треугольника, у которого есть 3 стороны – основание, высота и гипотенуза. Прямоугольные треугольники широко используются в тригонометрии. В прямоугольном треугольнике один угол равен 90°, а два других угла острые. Сторона, противоположная прямому углу, называется «гипотенуза», которая также является самой длинной стороной прямоугольного треугольника. Сторона, прилегающая к прямому углу, называется смежной стороной. Высота треугольника образует «противоположные стороны».
1. | Определение прямоугольного треугольника |
| 2. | Свойства прямоугольного треугольника |
| 3. | Построение прямоугольного треугольника |
| 5. | Решенные примеры построения прямоугольных треугольников |
| 6. | Практические вопросы по построению прямоугольных треугольников |
| 7. | Часто задаваемые вопросы о конструкциях прямоугольных треугольников |
Определение прямоугольного треугольника
Треугольник, один из внутренних углов которого равен 90°, называется прямоугольным. Самая длинная сторона прямоугольного треугольника называется гипотенузой. Длину самой длинной стороны прямоугольного треугольника можно найти с помощью теоремы Пифагора, которая гласит, что «Сумма квадрата гипотенузы равна сумме квадратов двух других сторон».
Свойства прямоугольного треугольника
Следующие точки являются свойствами прямоугольного треугольника.
- В прямоугольном треугольнике один из углов равен 90°
- Самая длинная сторона прямоугольного треугольника называется «Гипотенуза».
- Сумма внутренних углов прямоугольного треугольника равна 180°
- Сторона, лежащая напротив прямого угла, называется противоположной стороной, а сторона, лежащая рядом с прямым углом, называется прилежащей стороной.
- Площадь прямоугольного треугольника равна (1/2 × основание × высота)
- Если известны любые две стороны прямоугольного треугольника, мы можем легко построить треугольник.
- Одну из неизвестных сторон прямоугольного треугольника можно найти по формуле теоремы Пифагора — Гипотенуза = √Противоположная сторона 2 + Прилежащая сторона 2
Построение прямоугольного треугольника
Треугольник, в котором один из углов равен 90° — прямоугольный треугольник. Сторона, лежащая прямо напротив прямого угла, называется гипотенузой большей стороны. Чтобы построить прямоугольный треугольник, нам нужно измерить две его стороны. Циркуль и линейка необходимы для построения прямоугольного треугольника. Теперь давайте посмотрим, как треугольник PQR с гипотенузой 13 единиц и одной из его сторон равен 5 единицам.
Чтобы построить прямоугольный треугольник, нам нужно измерить две его стороны. Циркуль и линейка необходимы для построения прямоугольного треугольника. Теперь давайте посмотрим, как треугольник PQR с гипотенузой 13 единиц и одной из его сторон равен 5 единицам.
Шаг 1. Нарисуйте горизонтальную линию и отметьте на ней точку Q . Линия может быть любой длины.
Шаг 2: С Q в качестве центра, отмерьте 5 единиц компаса и нарисуйте дугу с обеих сторон точки так, чтобы дуга касалась горизонтальной линии, и отметьте точки как «S» и «R».
Шаг 3. Используя букву S в центре и отмерив 13 единиц по компасу, нарисуйте дугу над буквой S.
Шаг 4. При той же ширине в 13 единиц нарисуйте дугу из точки R. Отметьте точку пересечения этих дуг как «P».
Шаг 5. Соедините точки «P» и «Q», а также «P» и «R» с помощью линейки.
Шаг 6: Угол в точке Q равен 90°.
Темы, связанные с конструкциями прямоугольных треугольников
Ознакомьтесь с некоторыми интересными темами, связанными с конструкциями прямоугольных треугольников.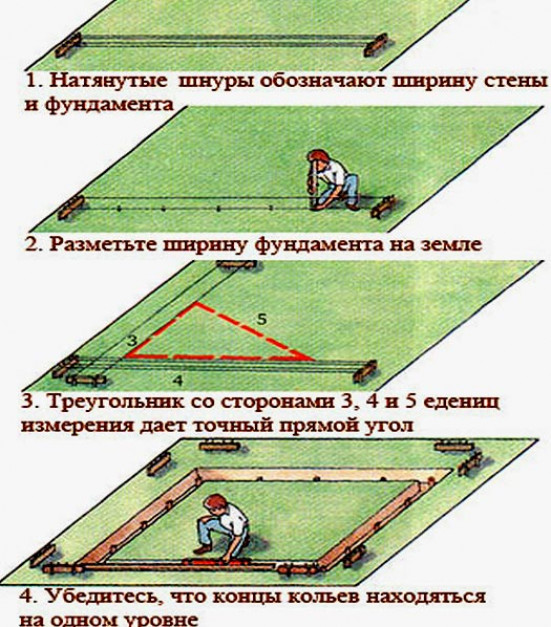
- Треугольники
- Высота треугольника
- Прямоугольный
- Углы
- Площадь прямоугольного треугольника
- Геометрия
Пример 1: Постройте прямоугольный треугольник ABC, где AC = 5 единиц, а BC = 3 единицы.
Решение:
Выполните следующие действия, чтобы построить прямоугольный треугольник ABC, AC = 5 единиц и BC = 3 единицы.- Шаг 1: Начертите горизонтальную линию и отметьте на ней точку «В».
- Шаг 2: С центром «В» и шириной в 3 единицы по компасу нарисуйте две дуги по обе стороны от линии и обозначьте их как «D» и «С».
- Шаг 3. С центром в точке D и шириной в 5 единиц по компасу нарисуйте дугу над буквой B и обозначьте ее как букву A.
- Шаг 4: Повторите тот же процесс с буквой «C» в качестве центра.
- Шаг 5. Соедините точку пересечения этих дуг с точками «B» и «C».
- Шаг 6: Отметьте угол B равным 90°.

Пожалуйста, обратитесь к рисунку ниже, чтобы увидеть, как будет выглядеть прямоугольный треугольник.
Пример 2. Измерения двух сторон прямоугольного треугольника следующие. Гипотенуза = 10 единиц, а противолежащая сторона = 6 единиц. как можно найти третью сторону, кроме метода построения с использованием циркуля и линейки?
Решение:
Мы можем сделать это, используя теорему Пифагора, Гипотенуза 2 = Противоположная сторона 2 + Прилежащая сторона 2 . Чтобы найти смежную сторону, мы можем переписать формулу следующим образом: Прилежащая сторона = √ Гипотенуза 2 — Противоположная сторона 2 . Сторона гипотенузы равна 10 единицам, а противоположная сторона – 6 единицам. Подставляя значения в формулу получаем, Смежная сторона = √ 10 2 — 6 2 = √ 100 — 36 = √ 100 — 36 = √ 64 = 8 единиц.
 Следовательно, длина прилежащей стороны треугольника равна 8 единицам.
Следовательно, длина прилежащей стороны треугольника равна 8 единицам.
перейти к слайдуперейти к слайду
Разбивайте сложные концепции с помощью простых визуальных средств.
Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций с помощью Cuemath.
Забронировать бесплатный пробный урок
перейти к слайдуперейти к слайдуперейти к слайду
Часто задаваемые вопросы о прямоугольных треугольных конструкциях
Что такое прямоугольный треугольник?
Прямоугольный треугольник — это тип треугольника, в котором один из его внутренних углов равен 90°. Сторона, противоположная самой длинной стороне, называется гипотенузой или самой длинной стороной.
Как называются стороны прямоугольного треугольника?
Гипотенуза — это наибольшая сторона прямоугольного треугольника, сторона, противоположная прямоугольному треугольнику, — это противоположная сторона, а сторона, лежащая рядом с прямым углом, называется прилежащей стороной.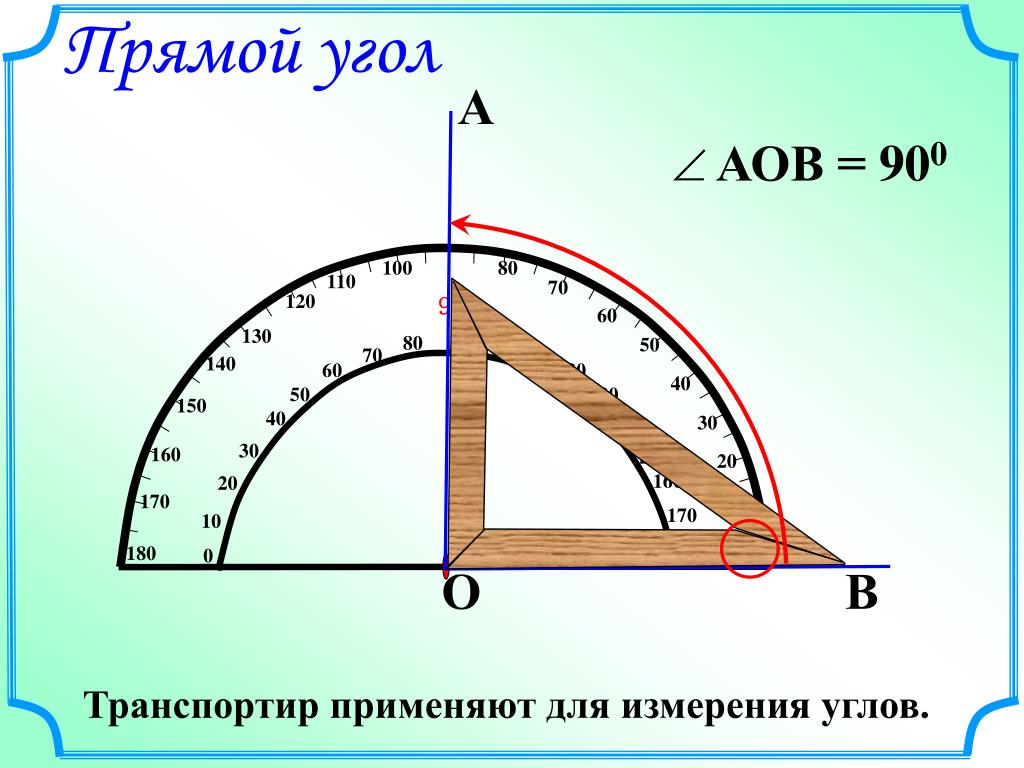
Что составляют углы прямоугольного треугольника в сумме?
Сумма углов прямоугольного треугольника равна 180°. (добавьте, что один угол равен 90 градусов, а два других являются острыми, но в сумме получится 180)
Как найти площадь прямоугольного треугольника?
Чтобы найти площадь прямоугольного треугольника, проверьте, заданы ли основание и высота, затем примените формулу = 1/2 x основание x высота.
Каковы свойства прямоугольного треугольника?
Некоторые важные свойства прямоугольного треугольника приведены ниже:
- Один из углов прямого угла всегда равен 90°.
- Сумма внутренних углов прямого угла равна 180°.
- Самая длинная сторона прямоугольного треугольника называется гипотенузой.
Скачать БЕСПЛАТНЫЕ учебные материалы
Рабочие листы под прямым углом
Рабочие листы по математике и
наглядный учебный план
Строительство угловых шкафов
Расчеты наклонных стен
На самом деле наклонные стены могут быть проблемой , большинство стен никогда не бывают прямыми углами. По этой причине при установке шкафа могут возникнуть проблемы. Невыполнение проекта вовремя может повредить хорошим отношениям с вашим клиентом (клиентами). Вы не хотите этого.
По этой причине при установке шкафа могут возникнуть проблемы. Невыполнение проекта вовремя может повредить хорошим отношениям с вашим клиентом (клиентами). Вы не хотите этого.
Как избежать ошибок
Использование программного обеспечения Pro100 устранит ошибки при установке. Видео ниже демонстрирует, как вы можете построить свои шкафы так, как вы это делаете в магазине. Посмотрите, как вырезанная задняя опора облегчает окончательную установку.
Программное обеспечение Custom Cabinet | Видео Lazy Suzan Construction — продолжительность 16:32.
Работа с наклонными стенами
Работа с наклонными стенами видео — 7:09 мин.
Использование
для создания точных угловых стен. Редактор форм — отличная функция Pro100 при работе с угловыми навесными шкафами. Ниже мы добавили небольшой инструмент, который вы можете использовать при расчете углов рядом с редактором форм. Просто введите необходимые размеры, и он сделает математику за вас.
| Угол a | Рассчитать | |
| Длина стороны B | ||
| Сторона C 90 016 | ||
| Сторона А | ||
| Угол b | 90 | |
| Угол c |
| Угол a | Рассчитать |
| Сторона A | |
| Сторона B | Сторона C |
| Угол b | 90 |
| Угол c |
Предупреждение. Когда вы создаете разделитель, подобный основному разделителю на этой странице, он работает только в том случае, если стороны A и Угол a одинаков для всех объектов. Угол b должен быть 90 градусов для работы.
| Сторона A | Рассчитать | |
| Угол a | 90 | Уголок b | 45 |
| Сторона B |
| Уголок a | Расчет | |
| Сторона B | ||
| Угол c | ||
| Сторона A |
| Сторона A | Рассчитать | |
| Угол a | 90 900 16 | |
| Угол b | ||
| Угол c | ||
| Сторона B | ||
| Сторона C |
Загрузки
Вы можете загрузить две распорки под углом 45 градусов и стенку со шкафами.

 , 3м. и 7м.). Далее по ним протягивается шнур от точки О, и если прямая совпадает со всеми точками — вы сделали правильно, если не совпадает — то перемеряем заново!
, 3м. и 7м.). Далее по ним протягивается шнур от точки О, и если прямая совпадает со всеми точками — вы сделали правильно, если не совпадает — то перемеряем заново!

 Следовательно, длина прилежащей стороны треугольника равна 8 единицам.
Следовательно, длина прилежащей стороны треугольника равна 8 единицам.