Внутренний объем погонного метра трубы в литрах — таблица. Внутренний диаметр трубы 4-1000 мм. Сколько нужно воды или антифриза или теплоносителя или, там, вазелина;) … для наполнения трубопровода. Пустяк, а времени такая табличка много экономит.
|
| о компании | ||||||||
Уважаемые Господа, мы рады приветствовать Вас на сайте ООО «БелСИ-ГП Автоматика». Наша компания имеет большой опыт, мы разбираемся в том, что продаем и надеемся быть Вам полезными. Основные направления деятельности: ● Мобильная и промышленная гидравлика ● Пневматика всегда в наличии в Минске ● проектирование и производство гидравлических станций, маслостанций, станций смазки, станций гидропривода; ● смазывающее и фильтрующее оборудование продажа и проектирование; ● клапаны соленоидные для жидкостей и газов подробнее | ||||||||
|
| |||||||
Как выбрать размер трубопровода сжатого воздуха?
Итак, Вам нужно узнать, как подобрать правильный размер трубопроводов сжатого воздуха. Все еще встречаются места, где размер трубы в системе сжатого воздуха слишком мал. Это либо потому, что производство со временем расширилось, и старая система стала слишком маленькой, или просто изначально были установлены неподходящие трубопроводы. В чем проблема со слишком маленькой трубой для сжатого воздуха? Это падение давления. Нужное количество сжатого воздуха попросту не пройде через эту трубу. Результатом будет является перепад давления между началом и концом трубы. Чем плох перепад давления? Это лишние затраты. Если падение давления становится слишком высоким, Вам нужно будет установить компрессор на более высокое давление. Чем оно выше, тем больше электроэнергии (и денег) он будет требовать. Поэтому желательно, чтобы падение давления составляло максимум 0,1 бар.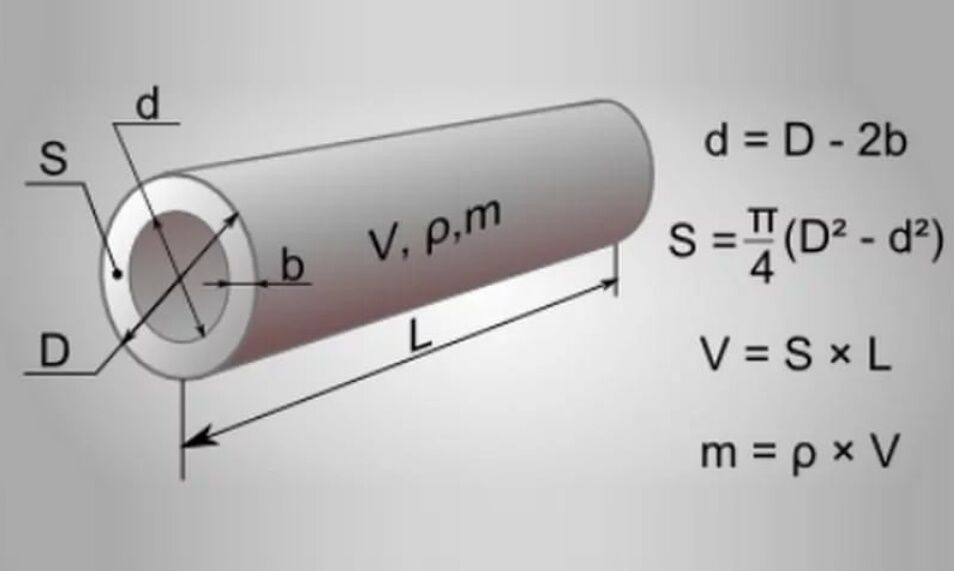
Что влияет на падение давления?
Конечно, не только сами трубы, но также повороты трубопровода, муфты, гибкие шланги, — все они создают перепады давления. И чем длиннее трубопровод, тем больше будет падение давления. Количество воздуха, проходящего через трубу, также влияет на величину перепада давления. Чем больше воздуха должно проходить через трубу в момент времени, тем больше падение давления. Поэтому падение давления нужно всегда измерять при всех включенных потребителях воздуха.
Ниже приведены величины, необходимые для расчета падения давления:
- диаметр трубы;
- длина трубы;
- количество изгибов, муфт и т. д.;
- поток воздуха через трубу.
Воздушный поток
Чтобы начать расчет, вам нужно знать, сколько воздуха проходит через вашу систему. Самый простой способ узнать (максимальный) расход воздуха — это посмотреть на характеристики вашего компрессора. Там всегда будет указана максимальная мощность машины в литрах в секунду, м3 в минуту или час. Есть также важная вещь. Производительность компрессора указана для стандартных условий, которые составляют 1 бар, 20 градусов по Цельсию и 0% относительной влажности. Однако производительность компрессора при нормальных условиях и фактическая производительность отличается. Таким образом, на самом деле производительность компрессора при нормальных условиях представляет собой количество воздуха, всасываемого компрессором в единицу времени. Затем воздух сжимается и транспортируется через систему трубопроводов. Таким образом, фактическая производительность компрессора будет ниже, чем производительность при нормальных условиях. Эта разница часто упускается из виду; большинство людей не знают об этом и неправильно пользуются характеристиками компрессорного оборудования.
Есть также важная вещь. Производительность компрессора указана для стандартных условий, которые составляют 1 бар, 20 градусов по Цельсию и 0% относительной влажности. Однако производительность компрессора при нормальных условиях и фактическая производительность отличается. Таким образом, на самом деле производительность компрессора при нормальных условиях представляет собой количество воздуха, всасываемого компрессором в единицу времени. Затем воздух сжимается и транспортируется через систему трубопроводов. Таким образом, фактическая производительность компрессора будет ниже, чем производительность при нормальных условиях. Эта разница часто упускается из виду; большинство людей не знают об этом и неправильно пользуются характеристиками компрессорного оборудования.
Таблица размеров труб для сжатого воздуха
Здесь представлена простая таблица, которая ответит на все вопросы по размерам трубопроводов. В левом столбце указана производительность компрессора. Теперь измерьте или рассчитайте общую длину Ваших трубопроводов сжатого воздуха и посмотрите на верхнюю строчку. Таким образом Вы можете узнать нужный диаметр трубы в мм. Эта таблица рассчитана на давление компрессора 7 бар и максимальный перепад давления 0,3 бар. Указанные значения относятся к прямой трубе без каких-либо поворотов, клапанов и т.д. Как рассчитать влияние этих факторов можно узнать из следующего абзаца.
Таким образом Вы можете узнать нужный диаметр трубы в мм. Эта таблица рассчитана на давление компрессора 7 бар и максимальный перепад давления 0,3 бар. Указанные значения относятся к прямой трубе без каких-либо поворотов, клапанов и т.д. Как рассчитать влияние этих факторов можно узнать из следующего абзаца.
Таблица 1: диаметры трубопроводов сжатого воздуха (в миллиметрах).
| Произв., м3/ч | 50 м | 100 м | 150 м | 300 м | 500 м | 750 м | 1000 м | 2000 м |
| 10 | 15 | 15 | 15 | 20 | 20 | 25 | 25 | 25 |
| 30 | 15 | 15 | 15 | 25 | 25 | 25 | 25 | 40 |
| 50 | 15 | 25 | 25 | 25 | 40 | 40 | 40 | 40 |
| 70 | 25 | 25 | 25 | 40 | 40 | 40 | 40 | 40 |
| 100 | 25 | 25 | 40 | 40 | 40 | 40 | 40 | 63 |
| 150 | 25 | 40 | 40 | 40 | 40 | 40 | 40 | 63 |
| 250 | 40 | 40 | 40 | 40 | 63 | 63 | 63 | 63 |
| 350 | 40 | 40 | 40 | 63 | 63 | 63 | 63 | 80 |
| 500 | 40 | 40 | 63 | 63 | 63 | 63 | 63 | 80 |
| 750 | 40 | 63 | 63 | 63 | 63 | 80 | 80 | 100 |
| 1000 | 63 | 63 | 63 | 63 | 63 | 80 | 80 | 100 |
| 1250 | 63 | 63 | 63 | 63 | 63 | 100 | 100 | 100 |
| 1500 | 63 | 63 | 63 | 80 | 80 | 100 | 100 | 125 |
| 1750 | 63 | 63 | 80 | 80 | 80 | 100 | 100 | 125 |
| 2000 | 63 | 80 | 80 | 80 | 100 | 100 | 100 | 125 |
| 2500 | 63 | 80 | 80 | 80 | 100 | 125 | 125 | 125 |
| 3000 | 80 | 80 | 76 | 100 | 100 | 125 | 125 | 150 |
| 3500 | 80 | 80 | 100 | 100 | 125 | 125 | 125 | 150 |
| 4000 | 80 | 100 | 100 | 100 | 125 | 125 | 125 | 150 |
| 4500 | 80 | 100 | 100 | 125 | 125 | 125 | 150 | 150 |
| 5000 | 80 | 100 | 100 | 125 | 125 | 150 | 150 | 150 |
Влияние изгибов, муфт и других составляющих трубопровода на падение давления
Ниже приведена таблица для определения того, как различные составляющие трубопровода влияют на перепад давления. Значение зависит от диаметра трубы. Чтобы узнать эквивалентную длину трубы для клапана или изгиб в вашей системе, просто посмотрите на диаметр трубы Вашей системы сжатого воздуха, чтобы найти эквивалентную длину трубы клапана или изгиб. Например, колено в 25-миллиметровой трубе имеет эквивалентную длину трубы 1,5 метра. Это означает, что это колено создаст такое же падение давления, как и 1,5 метра прямой трубы.
Значение зависит от диаметра трубы. Чтобы узнать эквивалентную длину трубы для клапана или изгиб в вашей системе, просто посмотрите на диаметр трубы Вашей системы сжатого воздуха, чтобы найти эквивалентную длину трубы клапана или изгиб. Например, колено в 25-миллиметровой трубе имеет эквивалентную длину трубы 1,5 метра. Это означает, что это колено создаст такое же падение давления, как и 1,5 метра прямой трубы.
Таблица 2. Эквивалентные длины труб (значения в метрах).
| Диаметр трубопровода | 25 мм | 40 мм | 50 мм | 80 мм | 100 мм | 125 мм | 150 мм |
| Изгиб 90° (R=d) | 0.3 | 0.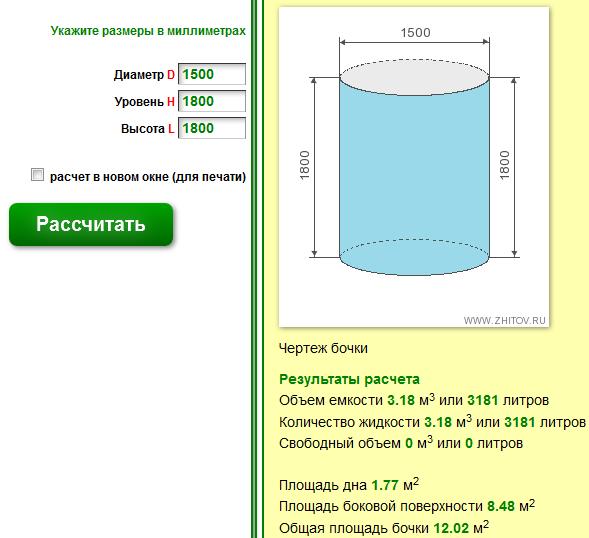 5 5 | 0.6 | 1.0 | 1.5 | 2.0 | 2.5 |
| Bend 90° (R=2d) | 0.15 | 0.25 | 0.3 | 0.5 | 0.8 | 1.0 | 1.5 |
| Колено (90°) | 1.5 | 2.5 | 3.5 | 5 | 7 | 10 | 15 |
| Т-образное соединение | 2 | 3 | 4 | 7 | 10 | 15 | 20 |
| Обратный клапан | 8 | 10 | 15 | 25 | 30 | 50 | 60 |
| Диафрагменный клапан | 1. 2 2 | 2.0 | 3.0 | 4.5 | 6 | 8 | 10 |
| Задвижка | 0.3 | 0.5 | 0.7 | 1.0 | 1.5 | 2.0 | 2.5 |
Пример расчета требуемого диаметра трубы
Предположим, у нас есть винтовой компрессор мощностью 30 кВт производительностью 250 Нм3/час (4200 Нл/мин. Есть также труба диаметром 40 мм и нам нужно проверить, правильно ли подобран ее диаметр.
Допустим, у нас есть 20 метров трубы с углом 90 градусов (R=2d означает, что радиус изгиба в 2 раза больше диаметра трубы) и обратный клапан, а затем снова 4 метра трубы.
Эквивалентная длина трубы для такого изгиба составляет 0,25 метра. Эквивалентная длина трубы для обратного клапана составляет 10 метров. Общая длина теперь составляет: 20 + 0,25 +10 + 4 = 34,25 метра.
Теперь мы можем найти требуемый диаметр трубы в таблице 1 для длины трубы 34,25 метра и производительности 250 Нм3/час. Получим диаметр трубы 40 мм.
Для новой системы, если Вы не уверены, сколько изгибов, клапанов и т.д будет в системе, умножьте длину трубопровода на 1.7.
Гидравлический расчет для выбора насосной станции.
Здравствуйте уважаемые читатели «Сан Самыча«. Смешно иногда слушать продавцов-консультантов, когда они пытаются искренне помочь «правильно» подобрать насосную станцию. Глубина всасывания, напор, расход, мощность электродвигателя, рассчитывая характеристики на ходу, они умудряются все перепутать и запутаться самим. Для нас, уважаемый читатель, важно понять, что производитель указывает максимально возможные характеристики насоса. И они, конечно, связаны с параметрами Вашей системы водоснабжения, но они не совпадают, и не могут совпадать.
Да, насос способен поднять воду с глубины в восемь метров, но тогда смело скидывайте с напора те же восемь метров или 0,8 бар (атмосфер, кгс/см2).
Да, насос выдаст 45 метров напора (4,5 бар, атм., кгс/см2), но при условии, что Вы не будете с него требовать расхода вообще, а источник воды будет на уровне насоса.
Да, насос будет перекачивать 50 литров в минуту (3 куб. метра в час), но тогда грех добиваться от него хоть какого-то давления. Радуйтесь, что он выдает Вам эти пять ведер в минуту!
Впрочем, производитель и не скрывает этого. В любом паспорте насоса и насосной станции можно найти зависимости расхода от давления на напоре данного насоса, оформленные в виде графика или таблицы. А уже сам покупатель решает: устраивают его данные характеристики или нет.
Что нужно для расчета характеристик насоса?
Для расчета необходимых характеристик насоса нужны некоторые сведения о будущей системе водоснабжения. И мне кажется, Вы, как хозяин своего дома без труда озвучите или выясните их.
К этим сведениям относятся:
— расстояние по вертикали от зеркала воды источника водоснабжения до предполагаемого места установки самого дальнего смесителя в метрах. Причем желательно учесть сезонные колебания этого расстояния и, так называемые, динамические, когда зеркало воды опускается из-за того, что Вы берете воду. Чем точнее Вы определите это расстояние, тем точнее будет расчет, потому что вертикальная составляющая потери напора, обычно, самая большая.
Причем желательно учесть сезонные колебания этого расстояния и, так называемые, динамические, когда зеркало воды опускается из-за того, что Вы берете воду. Чем точнее Вы определите это расстояние, тем точнее будет расчет, потому что вертикальная составляющая потери напора, обычно, самая большая.
— расстояние по горизонтали от источника воды до самого дальнего смесителя, рассчитанное исходя из предполагаемого маршрута прокладки трубы. Это расстояние можно измерить не так точно, точность плюс-минус один метр вполне сойдет.
— примерное предполагаемое место установки насоса или насосной станции в сборе. Соответственно, с вертикальным расстоянием, желательно, определиться поточнее.
— диаметры и материал предполагаемых к использованию в системе труб. Сейчас, обычно, используют пластиковые трубы, а у них у всех примерно равные показатели шероховатости, поэтому, по большому счету, значение имеют только диаметры предполагаемых труб и их длина. К слову, распространенная в интернете формула для расчета водоснабжения: 10 метров горизонтальной трубы равно 1 метру по вертикали, мягко сказать, не всегда верна. В дальнейшем я расскажу почему.
В дальнейшем я расскажу почему.
— Желательно, конечно, определиться с количеством уголков, тройников, кранов и других элементов системы, называемых «местными сопротивлениями». Но я понимаю, что это довольно сложно, по крайней мере, на данном этапе. Поэтому, по нашему обоюдному согласию, заменим это все, скажем, 10-процентным запасом по напору.
Ну, а при монтаже системы, не забывайте простое правило: Чем меньше соединений, тем меньше вероятность, что у Вас что-то потечет. К этому стоит добавить, что и потери напора тоже будут меньше.
Да!!!, и самое главное, Вы должны определиться, сколько потребителей (смесители, душ, бачок унитаза, стиральная или посудомоечная машина, уличный кран для полива и прочее) будут у Вас работать одновременно без существенной потери напора. Потому что от этого очень многое зависит.
Ниже, я собрал в таблицу потери напора в горизонтальной пластиковой трубе длиной 10 метров в зависимости от диаметра трубы и количества потребителей, рассчитанные с помощью специальной программы. По-моему, получилось очень показательно.
По-моему, получилось очень показательно.
Потеря напора в метрах водного столба на горизонтальном участке пластиковой трубы длиной 10 метров в зависимости от внутреннего диаметра трубы и количества потребителей.
Внутренний диаметр трубопровода | 12 мм | 16 мм | 20 мм | 26 мм |
1 потребитель (расход 0,2 л/с или 12 л/мин) | 4,05 | 1,0 | 0,35 | 0,1 |
2 потребителя (расход 0,4 л/с или 24 л/мин) | 14,09 | 3,49 | 1,16 | 0,33 |
3 потребителя (расход 0,6 л/с или 36 л/мин) | 29,49 | 7,23 | 2,52 | 0,7 |
Из таблицы видно, что формуле: 10 метров горизонтальной трубы равно 1 метру вертикальной, соответствует только труба внутренним диаметром 16 мм (это металлопластик или полипропилен наружным диаметром 20 мм) в расчете на одного потребителя. И это правило никак нельзя назвать универсальным.
И это правило никак нельзя назвать универсальным.
Стоит также добавить, что, даже заменяя участки существующей системы на трубы большего диаметра, Вы, тем самым, снижаете сопротивление трубопроводов системы в целом, увеличивая напор на выходе из смесителей.
Пример расчета характеристик насосной станции.
«Все это хорошо, — скажете Вы, — Но как же считать?!» Давайте посчитаем вместе.
Задача. Сделать гидравлический расчет водопроводной системы при условии что:
— Имеется скважина глубиной 18 метров, зеркало воды в которой находится на глубине не больше 10 метров от поверхности земли.
— Насос или насосную станцию предполагается поставить над скважиной в кессон глубиной 2,5 метра.
— От скважины до дома расстояние 13 метров.
— Внутри дома предполагаемое горизонтальное расстояние по маршруту прокладки трубы – 9 метров.
— Предполагаемые вертикальные расстояния: от пола до смесителя – 1,1 метра, от пола до излива душа – 2. 2 метра, от уровня земли до пола – 1,2 метра.
2 метра, от уровня земли до пола – 1,2 метра.
— Предполагаемая труба на всасе насоса: металлопластик наружным диаметром 26 мм и длиной 10 метров. На напоре: от насоса до дома – полиэтилен наружным диаметром 25 мм, длиной 18 метров, разводка в доме – полипропилен наружным диаметром 20 мм, длиной 9 метров.
— Рассчитывать нужно на использование одновременно двух потребителей.
Для начала, давайте приведем в порядок все эти сведения. Общее вертикальное расстояние от зеркала воды до самого дальнего потребителя (излив душа) будет равняться:
10 м + 1,2 м + 2,2 м = 13,4 метра.
Расстояние по вертикали от насоса до зеркала воды:
10 м – 2,5 м = 7,5 метров.
Горизонтальные расстояния нам, собственно, нужны только для определения длины труб, а эти сведения у нас уже есть. Длина трубы на всасе, которую нужно учесть при расчете – это расстояние от зеркала воды до насоса, т.е. 7,5 метров. В принципе, насос должен осилить эти метры, но это число нужно запомнить и проверить перед поиском подходящего насоса.
В принципе, насос должен осилить эти метры, но это число нужно запомнить и проверить перед поиском подходящего насоса.
Общая потеря напора по вертикали нами уже определена, это 13,4 метра. Теперь найдем потерю напора в трубах из-за движения по ним воды. Металлопластиковая труба наружным диаметром 26 мм имеет внутренний диаметр 20 мм, такой же внутренний диаметр у полиэтиленовой трубы, которую предполагается проложить от кессона к дому, поэтому:
18/10*1,16 = 2,088 м
Это потеря напора в полиэтиленовой (ПНД) трубе, ведущей к дому.
Особо не мудрствуя, я взял потерю напора для этого диаметра, 20 мм, и двух потребителей из своей же таблицы и нашел потерю напора для нужной нам длины трубопровода, помня о том, что в таблице указана потеря напора для длины в 10 метров.
Однако для оценки стабильности работы насоса нужно найти полное сопротивление трубы на всасе:
7,5/10*1,16 = 0,87 метра
и общая потеря напора на всасе будет равна:
0,87 + 7,5 = 8,37 метра,
что очень близко к критическим 9 метрам, максимально возможной глубине всасывания насоса.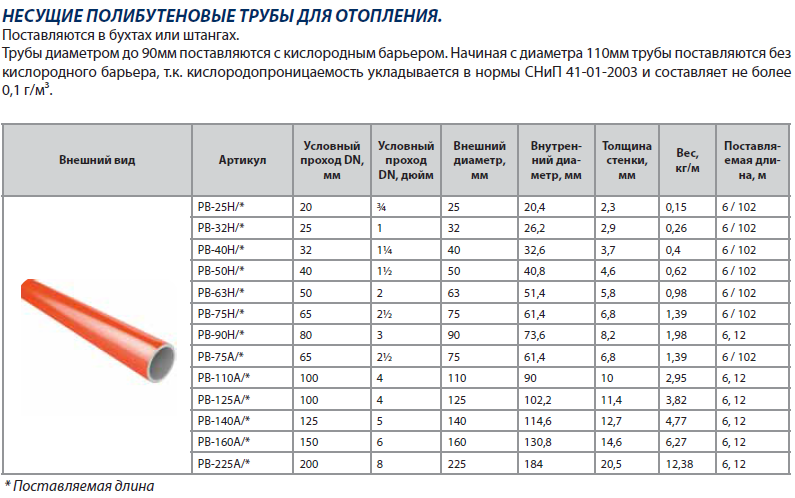 Поэтому, желательно, либо увеличить глубину кессона, хотя бы до 3 метров, либо использовать насосную станцию с внешним эжектором, что намного дороже. Еще вариант, увеличить диаметр всасывающего трубопровода до 32 мм, тогда общее сопротивление трубы уменьшится.
Поэтому, желательно, либо увеличить глубину кессона, хотя бы до 3 метров, либо использовать насосную станцию с внешним эжектором, что намного дороже. Еще вариант, увеличить диаметр всасывающего трубопровода до 32 мм, тогда общее сопротивление трубы уменьшится.
Давайте выберем вариант по надежней: увеличим диаметр трубы на всасе, поменяв её на металлопластик с наружным диаметром 32 мм (внутренний, соответственно, 26 мм) и «опустим» кессон на полметра. Общая высота подъема воды при этом нисколько не изменится. Мы лишь подвинем насос поближе к воде.
7/10*0,33 = 0,231 метра, и
7,0 + 0,231 = 7,231 метра,
Что уже вполне приемлемо, и с поиском нужного насоса, скорее всего, проблем не будет.
Полипропиленовая труба с наружным диаметром 20 мм имеет внутренний диаметр 16 мм, и потеря напора на ней составит:
9/10*3,49 = 3,141 метра
Теперь сложим все, что мы вычислили:
13,4 + 2,09 + 0,23 + 3,14 = 18,86 метра
И прибавим к этому оговоренные нами ранее десять процентов на потерю в местных сопротивлениях:
18,86 +10% = 20,75 метра.
Но это лишь тот напор, который должен преодолеть насос, чтобы вода просто полилась из смесителя. Чтобы вода пошла из смесителя под напором, к этому нужно добавить так называемый «свободный напор». По стандартам он должен быть не меньше 3 метров, исходя же из практических соображений, лучше закладывать в расчет число побольше, в разумных, конечно, пределах, например, 15 метров. Этого хватит на преодоление сопротивления в различном подключаемом нами оборудовании: бойлер, стиральная и посудомоечная машина и т.д.
Таким образом, мы получаем желательные характеристики насоса:
20,75 + 15 = 35,75, т.е. примерно 36 метров,
Но не меньше 20,75 + 3 = 23,75, т.е. примерно 24 метра.
При этих напорах насос должен выдавать нам 24 литра в минуту или 1,44 кубометра в час.
Напомню, это не те характеристики, которые написаны на шильдике насоса, а те, которые насос должен реально выдавать при этом напоре и расходе.
Как это узнать? Читаем дальше…
Как рассчитать объем емкости, цилиндрического резервуара? Формула расчета.
Расчет объема цилиндрической емкости производится для вычисление полезного объема и вместимости жидкости в цилиндрической емкости или пожарного резервуара чистой воды для пожаротушения.
Вычисление основных параметров объема цилиндрической емкости (резервуара пожаротушения) выполняется на основе геометрического метода расчета объема цилиндра, в отличии от метода калибровки, где расчет объема резервуара выполняется в результате реальных замеров вместимости жидкости по данным метрштока (мерной линейки). По результатам измерений создаются таблицы калибровки резервуаров — тарировочные таблицы цистерн для определения веса жидкости, перевозимой в цистерне, по объему и удельному весу, в зависимости от уровня налива жидкости, измеренной метрштоком.
Как рассчитать объем жидкости в емкости?
Опущенный в цилиндрическую емкость до нижнего положения метршток быстро, но плавно извлекается и по линии смачивания на нем определяется высота налива жидкости в емкости в сантиметрах. По уровню жидкости в сантиметрах для каждого калибровочного типа по соответствующей таблице калибровки можно рассчитать объем жидкости в емкости в кубических дециметрах (дм.куб). От правильности замера высоты налива жидкости зависит точность определения объема жидкости в емкости, а значит, и веса груза, поэтому на тщательность замера уровня жидкости должно быть обращено самое серьезное внимание.
По уровню жидкости в сантиметрах для каждого калибровочного типа по соответствующей таблице калибровки можно рассчитать объем жидкости в емкости в кубических дециметрах (дм.куб). От правильности замера высоты налива жидкости зависит точность определения объема жидкости в емкости, а значит, и веса груза, поэтому на тщательность замера уровня жидкости должно быть обращено самое серьезное внимание.
Формула расчета объема цилиндрической емкости (цилиндра)
V=S*L — расчет объема цилиндра,
где S — площадь поперечного сечения цилиндра, L — длина цилиндрической части.
Площадь поперечного сечения емкости в форме цилиндра рассчитывается по формуле:
S=3,14*d*d/4 — площадь круга с диаметром d.
Расчет объема цилиндрической емкости по формуле можно сделать как для горизонтальной, так и вертикальной накопительной емкости по их расположению. Фактически мы выполняем расчет объема цилиндра по всем известной формуле из геометрии. Расчет полезной вместимости цилиндрического резервуара можно посчитать более точно, если в формуле расчета объема горизонтальной емкости учесть толщину стенки — s. Внутренний диаметр определяют как.разность наружного диаметра и двойной толщины стенок обечайки, измеренной металлической линейкой или штангенциркулем.
Расчет полезной вместимости цилиндрического резервуара можно посчитать более точно, если в формуле расчета объема горизонтальной емкости учесть толщину стенки — s. Внутренний диаметр определяют как.разность наружного диаметра и двойной толщины стенок обечайки, измеренной металлической линейкой или штангенциркулем.
Длину цилиндрической части емкости определяют при помощи рулетки, измеряя расстояния между линиями пересечения днищ с цилиндрической частью резервуара. Если горизонтальный резервуар имеет плоские днища, то внутренний размер равен его наружной длине за вычетом двойной толщины днища.
Также не всегда удобно точно рассчитать диаметр емкости, для этого можно сделать измерение длины окружности, как решение, обхватить ее рулеткой. Измерить «длину окружности» гораздо легче, так как замер диаметра будет очень затруднителен в связи с тем, что сверху может находиться разного рода оборудование. К тому же можно произвести замер в трех разных сечених по объему резервуара чистой воды и сделать расчет среднего значения. Насчет «3 замеров» и «толщины стенки» — данные замеры параметров и их количество необходимо для минимизации погрешности расчета объема цилиндрической емкости, т.к. зачастую в процессе своей эксплуатации стенки теряют прочность, получают деформацию, уменьшаются в размерах и вместимость жидкости уменьшается.
Насчет «3 замеров» и «толщины стенки» — данные замеры параметров и их количество необходимо для минимизации погрешности расчета объема цилиндрической емкости, т.к. зачастую в процессе своей эксплуатации стенки теряют прочность, получают деформацию, уменьшаются в размерах и вместимость жидкости уменьшается.
Длину окружности обечайки измеряют не менее двух раз в каждом сечении. Обечайка в месте измерения должна имееть чистую поверхность, а натяжение рулетки віполняют с силой 5 кГ (50 Н) — определяются с помощью пружинного динамометра. В этом случае измерение окружности может быть проведено с погрешностью ±3 мм.
Выполнить измерение длины окружности цилиндрического резервуара Lокр, и тогда можно сделать расчет диаметра цилиндра по формуле:
d=Lокр/3,14
Рассчитать объем горизонтального резервуара можно аналогично расчету объема цилиндра (см. формулу выше). Сделав расчет объема резервуара можно округлить полученное значение, и выбрать ближайшее по стандартному ряду величин объемов емкости.
Как выбрать объем емкости, резервуара?
Если Вы хотите заказать изготовление тары, то объем емкости выбираем из ряда: 50 литров, 100л, 200л, 400 литров, 500 литров, 1 м куб, 2 м3 — или выбираем литраж 2000, 3 куба, 4 куб, на выбор 5м3 -или 5000 л, 8 куб,10 м3, 1 1 куб м, 15 м3, 20 куб, 25 м3, 30 м3, 40 м3, 50 куб, 75 куб, 100 м3, емкость 1000 м3 — резервуар РВС 1000. Под заказ можно выбрать объем по вашим размерам.
Расчёт корпуса и фильтров акустической системы
Конструирование акустических систем по готовым чертежам дело, конечно, увлекательное, но элемент творчества при этом, как ни крути, отсутствует. Вот если бы овладеть основными принципами построения АС, а затем все самому рассчитать и сделать из того, что есть под руками, — вот был бы класс! Это возможно, если взять несколько уроков у опытного мастера. Сегодня — первое занятие.
Все любители и специалисты, заинтересованные в достоверном воспроизведении звука, знают, что без хороших акустических систем не обойтись. Поэтому особенно озадачивают противоречия между различными взглядами на критерии качества АС. Ещё менее ясно, какие методы создания АС надежнее и приводят к приемлемым результатам.
Поэтому особенно озадачивают противоречия между различными взглядами на критерии качества АС. Ещё менее ясно, какие методы создания АС надежнее и приводят к приемлемым результатам.
Даже начального опыта прослушивания достаточно, чтобы заметить очень большую разницу между звучанием одной и той же музыки на разных моделях. При этом основной параметр — амплитудно-частотная характеристика (АЧХ) — почти всегда близок к идеалу, если верить данным фирм-производителей.
Большинство меломанов не может самостоятельно измерить АЧХ и приходит к выводу: проблема АЧХ практически решена, качество воспроизведения звука зависит от конструкции и материалов динамиков, корпусов, кроссоверов. Например: катушка без сердечника — хорошо, с сердечником — хуже. Или: корпус весом в 40 кг лучше, чем 20-килограммовый, при тех же габаритах и т.д.
Разумеется, оспаривать влияние динамиков, корпусов, элементов кроссовера, кабелей внутренней разводки, звукопоглотителей и прочих составляющих было бы ошибкой, но всё ли в порядке с АЧХ? Независимые измерения, например, в хорошо оснащённых лабораториях авторитетных зарубежных и отечественных аудиожурналов, не подтверждают оптимистических параметров, заявленных производителями.
На практике каждая модель АС имеет свою кривую АЧХ, разительно отличающуюся от других разновидностей колонок, причем это относится к любой ценовой группе. Наблюдаемая разница многократно превосходит порог заметности, известный из психоакустики, ее просто невозможно не услышать. И слушатели её, конечно, замечают как различие тембрального баланса при воспроизведении одних и тех же композиций разными АС. Идентифицировать искажения тембра с проблемами равномерности АЧХ нелегко, ведь перед глазами — ровные, будто по линейке нарисованные характеристики от изготовителя.
Не факт, что эти изумительные графики — обман. Просто для рекламы измерения производятся по методикам, обеспечивающим «благообразный» вид кривых. Например, при повышенной скорости сканирования рабочего диапазона в сочетании с высокой инерционностью, то есть усреднением пиков и провалов при регистрации зависимости звукового давления от частоты.
Производителей можно понять, в конце концов, все мы хотим выглядеть несколько лучше, чем на самом деле, и поэтому причёсываемся, умываемся и т. д. перед ответственными встречами.
д. перед ответственными встречами.
Гораздо интереснее другое: почему одна АС с «плохой» АЧХ звучит хорошо, а другая, может быть, обладающая менее безобразной характеристикой, — гораздо хуже? Независимые, более «честные» измерения выявляют несовершенство передачи тембрального баланса из-за особенностей АЧХ, но не помогают интерпретировать, расшифровать смысл «перегибов» и дисбалансов характеристик, раскрыть связь между поведением кривой и конкретными особенностями звучания АС. Вот подходящее сравнение: кардиограмма ничего не говорит обычному человеку, тогда как врач-специалист способен прочитать по ней состояние пациента.
Наша сегодняшняя задача — научиться анализировать АЧХ. Начнём с самого общего вопроса. Почему, обладая всем необходимым, разработчики не создают идеальной, одинаково хорошо звучащей акустики. Ведь идеал, эталон — только один! Очевидно, что все колонки, близкие к нему, будут звучать очень похоже. Существует ряд общепризнанных методик обеспечения «ровной» АЧХ, и одна из основных — настройка АС в заглушенной, безэховой камере. Есть и другие, вроде бы логичные и адекватные методы, например, настройка по импульсным сигналам. Но работая по одинаковым алгоритмам, специалисты каждый раз получают разный результат. Вспомните откровения авторитетных зарубежных мастеров, опубликованные в аудиопрессе: «… обеспечив идеальную АЧХ в звукомерной камере, мы потом «портим» эту характеристику для получения приемлемого звучания в обычных условиях…». Не пора ли прекратить молиться на равномерность АЧХ с точки зрения некой общеизвестной методики измерения?
Есть и другие, вроде бы логичные и адекватные методы, например, настройка по импульсным сигналам. Но работая по одинаковым алгоритмам, специалисты каждый раз получают разный результат. Вспомните откровения авторитетных зарубежных мастеров, опубликованные в аудиопрессе: «… обеспечив идеальную АЧХ в звукомерной камере, мы потом «портим» эту характеристику для получения приемлемого звучания в обычных условиях…». Не пора ли прекратить молиться на равномерность АЧХ с точки зрения некой общеизвестной методики измерения?
Ведь любой способ измерения в науке и технике неизбежно даёт целый комплекс разносортных ошибок. В нашем случае самые вредные ошибки — методические, то есть связанные с несовершенством самого подхода. Например, где располагать микрофон относительно АС в звуковой камере? На акустической оси? А где эта ось? Перед ВЧ-динамиком? А если он воспроизводит начиная с 8 кГц? Тогда, видимо, точнее мерить на оси СЧ-динамика? А если сместить микрофон на 5 см выше? Получим совсем другую АЧХ. На какую ориентироваться? И почему мы думаем, что ухо слушателя окажется именно там, где находился микрофон?
На какую ориентироваться? И почему мы думаем, что ухо слушателя окажется именно там, где находился микрофон?
Кроме того, на НЧ и нижней середине АС активно взаимодействует с полом, влияние которого в безэховой камере отсутствует.
Об интеграции излучения АС с помещением прослушивания в данный момент даже и разговор не будем начинать. Это взаимодействие очень сильно влияет на звучание, но его конкретные проявления бесконечно разнообразны, поэтому не умещаются в «ложе» какой-либо математической модели, с достаточной точностью необходимой для действительно высокого качества воспроизведения.
Ещё интересный факт: в реальном помещении суммарная АЧХ двух АС стереопары, даже при сильном усреднении, сильно отличается от АЧХ одной АС. Традиционные методики настройки АС не учитывают этого важного обстоятельства. Это недопустимо, так как главные персоны в музыке — солисты — чаще всего локализуются в центре звуковой сцены, то есть — воспроизводятся обеими АС.
Можно сделать вывод: при таком обилии методических ошибок обычные способы контроля АЧХ дают неправильную характеристику для реально очень ровных АС (например, Audio Note, Magnepan и т.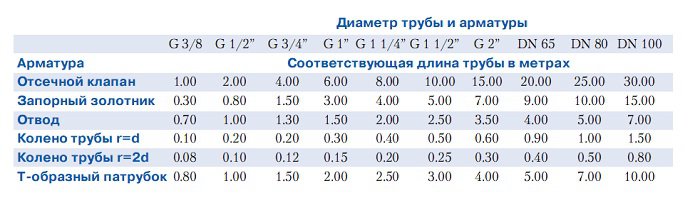 д.). С другой стороны, крайне подозрительно выглядят полученные по ненадёжным методикам слишком гладкие АЧХ. В этом случае ошибки измерений скомпенсированы специально сформированной характеристикой, которую разработчик обеспечивает, слепо доверяя не оправдавшим себя на практике способам измерений.
д.). С другой стороны, крайне подозрительно выглядят полученные по ненадёжным методикам слишком гладкие АЧХ. В этом случае ошибки измерений скомпенсированы специально сформированной характеристикой, которую разработчик обеспечивает, слепо доверяя не оправдавшим себя на практике способам измерений.
Меньше всего мне хотелось бы заменять веру в одни несовершенные принципы верой в другие, мои. Они тоже далеко не идеальны, в них присутствуют заметные методические ошибки, только менее грубые.
Залог прогресса — понимание недолговечности роли достигнутых знаний и умений, готовность воспринимать, в процессе практической работы и исследований, новые открытия. Надо уметь пересматривать подходы к достижению лучших результатов, если количественный рост позволяет совершить качественный скачок.
Итог работы зависит от методов и развития личности создателя АС. Известны превосходные изделия, рожденные в рамках традиционных подходов, при условии высочайшего класса и опыта разработчиков.
Моя цель — вооружить всех желающих достаточно эффективной методикой создания АС с приемлемым звучанием. Длинное вступление было необходимо для того, чтобы обратить ваше внимание на факторы, мешающие развивать искусство настройки АС.
Мне бы хотелось передать свой опыт, не тратя на это непомерных «писательских» усилий. Поэтому буду рассказывать только о добытых на практике фактах и методах работы, без обоснований и теоретических объяснений. Мой принцип — уверенно излагать своё мнение можно, если имеется аудиосистема, хорошим звучанием подтверждающая рекомендации автора. Для доступности расчёты и приёмы настройки максимально упрощены, без существенного вреда для результата.
Урок первый. Корпус
В первую очередь ограничим необъятную тему. Рассмотрим разработку и настройку двух полосных АС с фазоинвертором (ФИ). Такой тип легче «поддаётся» новичкам. Договоримся, что озвучиваем жилую комнату 10 — 20 м². Это определяет выбор диаметра НЧ/СЧ-динамика. В этом случае оптимальный диаметр диффузора — 10 — 20 см (примерно).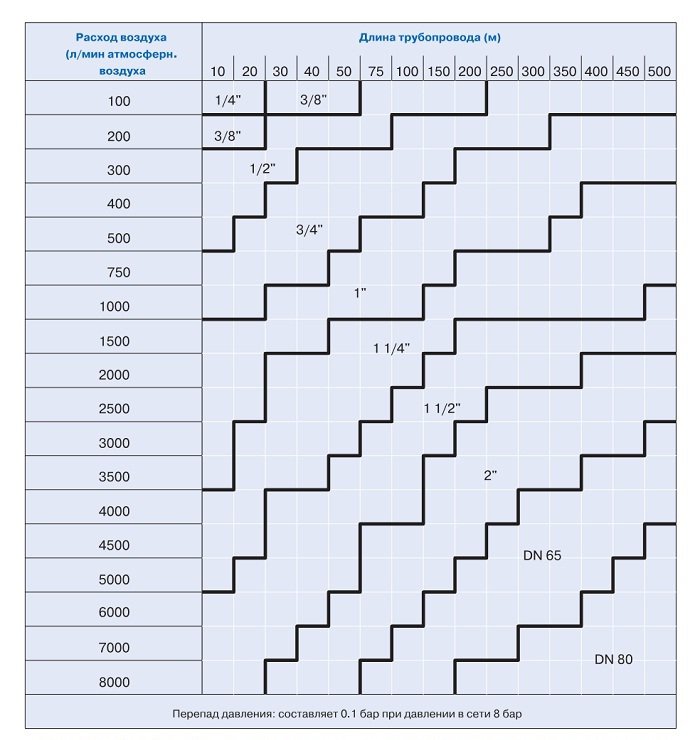 Паспортная мощность (100 часов разового шума без повреждения громкоговорителя) — 20 — 60 Вт. Чувствительность — 86 — 90 дБ/Вт/м. Резонансная частота (вне корпуса) — не выше 60 Гц. Если вас устроит нижняя граничная частота (готовой АС) 100 Гц, можно брать динамик с резонансом 80 — 100 Гц.
Паспортная мощность (100 часов разового шума без повреждения громкоговорителя) — 20 — 60 Вт. Чувствительность — 86 — 90 дБ/Вт/м. Резонансная частота (вне корпуса) — не выше 60 Гц. Если вас устроит нижняя граничная частота (готовой АС) 100 Гц, можно брать динамик с резонансом 80 — 100 Гц.
Кстати, если АС без завала воспроизводит хотя бы от 100 Гц, звучание вполне фундаментально и «весомо», только иногда исчезают некоторые необязательные, но очень желательные элементы звуковой картины. Их можно восстановить сабвуфером, но чтобы при этом не испортить звук, надо набраться опыта его согласования с сателлитами.
Не обольщайтесь по поводу паспортных данных недорогих АС, свидетельствующих о воспроизведении НЧ от 30 до 40 Гц. Реально в формировании звуковой картины участвуют только те низкие ноты, которые отыгрываются без «завала». Всё, что имеет спад хотя бы 4 — 5 дБ, маскируется «верхним басом» (80 — 160 Гц), поэтому для большинства АС воспринимаемый на слух диапазон начинается с 50 — 80 Гц. Мы же привыкли думать, что это 30 — 40 Гц, поскольку ориентируемся на паспортные данные с допустимым отклонением -8 — -16 дБ. Повнимательнее посмотрите в аудиопрессе на реальные частотные характеристики колонок. Отмерьте, в соответствии с приведённым масштабом, -3 дБ от среднего уровня, и вы увидите, что даже крупные напольные АС эффективно работают где-то от 50 Гц.
Мы же привыкли думать, что это 30 — 40 Гц, поскольку ориентируемся на паспортные данные с допустимым отклонением -8 — -16 дБ. Повнимательнее посмотрите в аудиопрессе на реальные частотные характеристики колонок. Отмерьте, в соответствии с приведённым масштабом, -3 дБ от среднего уровня, и вы увидите, что даже крупные напольные АС эффективно работают где-то от 50 Гц.
Если диаметр диффузора — 10 — 12 см, чувствительность — 86 — 88 дБ/Вт/м, а мощность — 20 — 30 Вт (типичные параметры недорогого динамика), то о «домашней дискотеке» придётся забыть. С другой стороны, громкоговорители минимального диаметра нередко имеют более равномерную АЧХ, чем большие.
«Малыши» лучше по ширине и равномерности диаграммы направленности. Интересно, что одна из высочайших по качеству АС фирма System Audio принципиально использует только маленькие мидбасовые динамики. Полная добротность современных небольших НЧ-головок обычно составляет 0,2 — 0,5.
Не надейтесь на расчёты низкочастотного оформления, практические результаты им соответствуют недостаточно точно. Опыт показывает: лучше выбрать динамики с добротностью больше 0,3 — 0,4, иначе, даже с фазоинвертором, трудно обеспечить приемлемый бас. Для таких громкоговорителей имеет смысл изготавливать корпуса объёмом, примерно равным эквивалентному объёму громкоговорителя.
Опыт показывает: лучше выбрать динамики с добротностью больше 0,3 — 0,4, иначе, даже с фазоинвертором, трудно обеспечить приемлемый бас. Для таких громкоговорителей имеет смысл изготавливать корпуса объёмом, примерно равным эквивалентному объёму громкоговорителя.
Очень ориентировочно для рекомендуемых по параметрам динамиков эквивалентный объём соответствует диаметру:
10 см — ≈ 18 литров;
16 см — ≈ 26 литров;
20 см — ≈ 50 литров.
В качестве базисного варианта рассмотрим корпус с ФИ для громкоговорителя диаметром 16 см. Объём — 26 литров. Площадь сечения ФИ — 44 см². Длина трубы ФИ — 20 см. Частота настройки — около 40 Гц. Площадь сечения ФИ должна составлять 20 — 25% от площади диффузора Sд.
Sд = π • (d/2)²,
где d — диаметр диффузора, ограниченный серединой подвеса (рис. 1).
Рис. 1
Если необходимо пересчитать габариты трубы ФИ для другого «литража» (другой диаметр динамика), сохраняя частоту настройки, действуйте в соответствии с примерами:
1. Громкоговоритель d = 9 см, Эквивалентный объём (Vэ) ≈ 8 л. 8 литров меньше 26 литров в 3,25 раза. Надо скомпенсировать разницу изменением длины (l) и площади (Sфи) трубы ФИ, иначе частота резонанса ФИ резко повысится.
Громкоговоритель d = 9 см, Эквивалентный объём (Vэ) ≈ 8 л. 8 литров меньше 26 литров в 3,25 раза. Надо скомпенсировать разницу изменением длины (l) и площади (Sфи) трубы ФИ, иначе частота резонанса ФИ резко повысится.
Понижают частоту настройки Fфи увеличением lфи и снижением Sфи.
Оптимальная Sфи для динамика площадью:
Sд = π (9 см/2)² = 3,14 • (4,57 см)² ≅ 63,6 см²
находится в диапазоне:
Sфи ≈ 63,6 см²/5 … 63,6 см²/4 ≅ 13 см² … 16 см².
В данном случае уменьшение Sфи вносит вклад в понижение Fфи в
44 см²/(13 см² … 16 см²) ≈ 2,75 … 3,38 разa,
что вполне компенсирует изменение объёма АС в 3,25 раза.
Кстати, компенсировать снижение объёма увеличением длины трубы ФИ для маленького корпуса (V = 8 литров) невозможно. Тем более что от внутреннего среза трубы ФИ до ближайшего препятствия (до стенки корпуса АС) должно быть свободное расстояние не менее 8 см (в крайнем случае — 5 см). То есть один из габаритов корпуса (параллельный оси трубы ФИ) должен быть равен lфи (20 см) + 8 см (свободное пространство) + примерно 3 см (толщина двух стенок корпуса) = 31 см.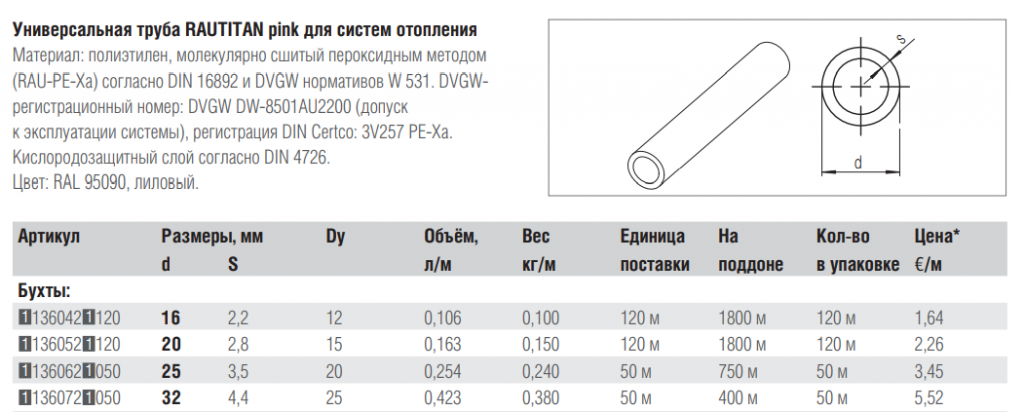
Для 8-литрового корпуса такой большой размер может быть только высотой. Возможная конструкция щелевого ФИ с прямоугольным сечением трубы показан на рис. 2а.
Рис. 2
Это очень непрактичная конструкция, так как требуется установка на специальную подставку, не загораживающую выход ФИ. Если вывести порт наверх, установка АС упростится, но вид сверху ухудшится, кроме того, колонка превратится в отличную ловушку для пыли, сора и мелких предметов.
Очень удобна конструкция, показанная на рис. 2б. Однако она требует увеличить высоту до 31 см + 8 см = 39 см. Это не всегда допустимо.
Можно изготовить корпус в виде глубокой «буханочки», с наибольшим размером — в глубину (рис. 2в).
Если не удаётся обеспечить нужную длину трубы, можно:
во-первых, выбрать минимальную
Sфи = Sд / 6; Sфи = 63,6 см² / 6 ≈ 10,6 см²;
во-вторых, несколько уменьшить lфи (≈ на 30 %), пожертвовав повышением Fфи до ≈ 50 — 60 Гц.
Уменьшение Sфи до 10,6 см² снизит эффективность ФИ и, соответственно, увеличит «завал» отдачи в диапазоне 40 — 60 Гц.
Рост Fфи при уменьшении lфи допустим, так как резонансная частота динамика диаметром 10 см выше, чем у громкоговорителя 16 см. Это значит, что ФИ с резонансом в 55 Гц не просуммирует свой подъём НЧ с резонансом динамика в ящике (≈ 70 — 90 Гц в данном случае) и не будет вредного для звучания подъёма на НЧ в области 50 — 100 Гц, который мог бы возникнуть, например, при укорочении ФИ для корпуса с динамиком 16 см.
Итак, для 8-литрового ящика и громкоговорителя диаметром 10 см вполне нормально выбрать lфи ≅ 14 см, Sфи ≅ 13 см².
2. Громкоговоритель d = 18 см, эквивалентный объём (Vэ) ≈ 50 л. 50 литров больше, чем 26 литров, в 1,92 раза.
Оптимальная Sфи для динамика площадью:
Sд ≅ 3,14 • (18 см / 6)² ≈ 254,3 см²
находится в диапазоне
Sфи ≈ 254,3 см²/5 … 254,3 см²/4 ≈ 51 см² … 64 см².
Увеличение Vэ в 1,92 раза сильнее влияет, чем увеличение Sфи в 1,45 раза. В целом Fфи понижается ориентировочно до 35 Гц. Так как резонансная частота динамика (Fд) диаметром 20 см ниже, чем Fд диаметром 16 см, то снижение Fфи — положительный фактор. Не стоит компенсировать это уменьшением lфи.
Не стоит компенсировать это уменьшением lфи.
Опытные профессионалы способны точно настраивать параметры фазоинверсного акустического оформления, добиваясь максимально плоской АЧХ в диапазоне от нижней граничной частоты АС до 125 — 200 Гц. Любителю или новичку не стоит тратить на это особых усилий.
В дальнейшем я поясню, как проконтролировать полученную АЧХ на НЧ и как устранить недопустимые отклонения, если таковые обнаружатся. Кроме того, влияние на звучание неидеальности характеристики в области НЧ сильно зависит от соотношения уровня воспроизведения баса по сравнению со средними частотами. Нельзя забывать, что из-за взаимодействия АС с реальным помещением АЧХ в нижнем регистре в любом случае будет очень неравномерной.
Главные усилия необходимо сосредоточить на настройке желаемой АЧХ в области СЧ и балансировке между НЧ, СЧ и ВЧ. На первом этапе создания АС — при разработке корпуса, достаточно учесть следующие рекомендации.
Корпус должен молчать. В идеале воспроизводят звук только громкоговорители, но в реальной жизни корпус откликается на их работу. Переизлучение звука стенками ящика вносит искажения.
Переизлучение звука стенками ящика вносит искажения.
Один из простейших способов улучшения виброзащиты корпуса — увеличение толщины стенок. Здесь следует знать меру, прослушивание показывает, что начиная с некоторого значения эта мера даёт незначительноё улучшение звучания. Для полочных АС вполне достаточно будет 16 — 8 мм ДСП или ДВП. Выгодно укреплять корпус изнутри рёбрами жёсткости. Вариант их практического использования показан в моей статье «Повторение возможно» в «Практике» №2(4)/2002, июль).
Там же достаточно подробно изложены рекомендации по следующим вопросам:
- размещение звукопоглощающих материалов внутри корпуса;
- особенности изготовления фильтров;
- как самостоятельно сделать кабели для внутренней разводки очень высокого качества;
- требования к герметизации корпуса;
- минимальные сведения, необходимые для выбора типа конденсаторов.
В упомянутой статье также рассмотрены вопросы выбора динамиков и затронуты некоторые другие проблемы. Имеет смысл отнестись к этому как к части изложения моих методов работы, поэтому повторяться не стану.
Имеет смысл отнестись к этому как к части изложения моих методов работы, поэтому повторяться не стану.
Разумеется, существует много способов виброзащиты корпуса АС. Они приведены, например, в книге «Высококачественные акустические системы и излучатели» (И.А. Алдошина, А.Г. Войшвилло. — М.: Радио и Связь, 1985.). Практика показывает, что 16-миллиметровые стенки, укреплённые рёбрами жёсткости, обеспечивают достаточную виброзащиту.
Абсолютных истин нет. У акустически мёртвых корпусов есть альтернатива — использование массива различных пород дерева, каждая из которых обладает собственным звучанием. Это — трудный путь с технологическими и творческими проблемами. Он не для новичков, здесь требуется высшая квалификация в области деревообработки, тонкое восприятие музыки, упорство в поиске приемлемых вариантов исполнения корпуса. Иногда таким образом удаётся создать превосходные АС.
Урок второй. Фильтры
Если вы думаете, что фильтр это просто схема, разделяющая сигнал на несколько частотных полос для соответствующих громкоговорителей, то вынужден буду вас разочаровать. Всё гораздо сложнее. Простой кроссовер нужен для идеальных динамиков с ровной АЧХ по звуковому давлению, но таковых, к сожалению, не существует. В лучшем случае некоторые типы динамиков позволяют обеспечивать приблизительно приемлемую балансировку АЧХ при лобовом использовании кроссоверов.
Всё гораздо сложнее. Простой кроссовер нужен для идеальных динамиков с ровной АЧХ по звуковому давлению, но таковых, к сожалению, не существует. В лучшем случае некоторые типы динамиков позволяют обеспечивать приблизительно приемлемую балансировку АЧХ при лобовом использовании кроссоверов.
Положение усложняется из-за сложного взаимодействия громкоговорителей в полосе передачи эстафеты от низкочастотного к более высокочастотному. Например, имеем замечательно ровные в своих полосах СЧ и ВЧ-головки с аккуратными спадами АЧХ вне полос, а при совместной работе получаем ужасную АЧХ. Особенно проблематично для новичка состыковать НЧ и СЧ-динамики. Приёмы такого бесшовного соединения — тема отдельной статьи. Для начала необходимо набраться опыта, настраивая двухполосную АС.
Даже самые простые фильтры — мощный инструмент в умелых руках, позволяющий приблизить АЧХ реальной АС к желаемому идеалу. Для НЧ/СЧ-головок фильтры первого порядка (катушка индуктивности, включенная последовательно с динамиком) чаще всего не подходят. Они недопустимо деформируют АЧХ в полосе пропускания, заваливают середину, делая звучание тусклым, неритмичным, монотонно гудящим. В некоторых случаях такой фильтр позволяет чуть скорректировать АЧХ в верхней части диапазона, воспроизводимого НЧ/СЧ-головкой. При этом частота среза такого фильтра близка верхней частоте динамика.
Они недопустимо деформируют АЧХ в полосе пропускания, заваливают середину, делая звучание тусклым, неритмичным, монотонно гудящим. В некоторых случаях такой фильтр позволяет чуть скорректировать АЧХ в верхней части диапазона, воспроизводимого НЧ/СЧ-головкой. При этом частота среза такого фильтра близка верхней частоте динамика.
У редких головок наблюдается рост отдачи, пропорциональный повышению частоты сигнала на протяжении нескольких октав. Сбалансировать АЧХ в этих случаях можно индуктивностью фильтра первого порядка, но чаще для этого применяют фильтры второго порядка. Они позволяют исключить сильные искажения АЧХ в полосе пропускания.
Подбором сочетаний величин ёмкости и индуктивности фильтра второго порядка можно обеспечить в полосе около частоты среза спад или подъём АЧХ, используя схему в качестве эквалайзера. Это — один из методов оптимизации АЧХ.
На рис. 3 показан фильтр второго порядка. Ёмкость включена параллельно динамику.
Рис. 3
Первое приближение
Рассчитаем значения L1 и С1 для фильтра без подъёма или спада на частоте среза. Поверим значению импеданса, приведённому производителем. Если бумажек нет, померяйте сопротивление по постоянному току и умножьте результат на 1,25. Обозначим полученное значение просто R.
L1 = R / (2π • Fc),
где Fс — частота среза,
C1 = 1 / ((2π • Fc)² L1).
Например: R = 4 Ом, Fс = 1,6 кГц.
L1 = 4 / (6,28 • 1.6 • 10³) = 3,98 • 10-4 H = 0,398 mH = 398 μH,
C1 = 1 / [(6,28 • 1,6 • 10³)² • 3,98 • 10-4] = 2,49 • 10-5 F = 24,9 μF.
Для справки:
Fc = 1 / (2π √L1 C1).
В этом случае модули (величины без учёта фазы) сопротивления L1 и C1 на частоте Fс равны R, то есть 4 Ом. Кстати, на частоте среза модули сопротивления L1 и C1 всегда равны.
Если выравнивание АЧХ требует подъёма на Fc, скажем, на 1 дБ, то есть примерно но 10%, необходимо снизить модули сопротивления L1(|ZL1|) и C1(|ZC1|) примерно на 10% по сравнению с R = 4 Ом, то есть до 4 Ом x 0,9 = 3,6 Ом.
L1 = 3,6 / (6,28 • 1,6 • 10³) = 3,58 10-4H = 0,358 mH = 358 μH.
C1 = 1 / [(6,28 • 1,6 • 10³)² • 3,58 • 10-4] = 2,77 • 10-5 F = 27,7 μF.
Частота среза остаётся прежней, но на Fс на головку подаётся ≈110% сигнала за счёт повышенного потребления тока от усилителя и преобразования его «звенящим» фильтром с добротностью больше единицы в форсированный сигнал на головке.
Если надо «завалить» область около Fc на 1 дБ, то нужно пересчитать фильтр, как будто его нагрузка — сопротивление динамика примерно 1,1 x 4 Ом = 4,4 Ом.
Проще получить нужные значения, увеличив L1 и уменьшив С1. Тогда Fc не изменится, а |ZL| и |ZC| будут равны 4,4 Ом.
L1 = 398 mН x 1,1 = 438 mН.
С1 = 24,9 mF x 1,1 = 22,64 mF.
Для справки:
|ZL1| = 2π • F • L1, |ZC1| = 1 / (2π • F • C).
Учтите, что при необходимости увеличения отдачи в области около FC придётся смириться с падением импеданса АС в этой же области.
Падение импеданса необходимо контролировать. Попробуйте следующий простой способ.
1 этап
Подключите к выходу вашего усилителя цепь, показанную на рис. 4а.
Рис. 4
На этом рисунке значок «+» соответствует красной клемме, а «-» — чёрной. На результаты измерений перемена полярностей не влияет.
Подайте на вход усилителя синусоидальный сигнал частотой 1 кГц от генератора. Регулятором громкости усилителя и регулятором выходного уровня генератора установите на выходных клеммах усилителя ≈1 В действующего напряжения. Для этого вам понадобится вольтметр, способный измерять действующее значение напряжения в области звуковых частот.
Переключите вольтметр для измерения напряжения на выходах резистора R2. Прибор покажет ≈38,5 мВ. Подрегулируйте уровень сигнала до показаний вольтметра ≈40 мВ.
2 этап
Подключите вашу АС вместо R2. Плавно изменяйте частоту сигнала на выходе генератора. Вы увидите, что показания вольтметра меняются. Эти изменения пропорциональны частотно-зависимому значению импеданса АС. Можно зарисовать измеряемую характеристику: по горизонтальной оси будет шкала частоты, по вертикальной — уровня напряжения. И то и другое выполняется в логарифмическом масштабе. (Пример пустого бланка будет опубликован в следующем номере «Практики AV».) Особенно внимательно ищите минимумы напряжения, плавно меняя частоту. Эти точки на характеристике соответствуют минимумам импеданса АС.
С достаточной точностью можно считать, что значение импеданса |ZAC| равны показаниям вольтметра, поделённым на 10.
Например, 40 мВ соответствует 4 Ом, 30 мВ — 3 Ом. Если у вас нет чувствительного вольтметра, то поможет хороший тестер. В режиме измерения переменного напряжения тестер является вольтметром. Его показания верны до 2 — 5 кГц, выше может быть существенная погрешность. Сверьтесь с паспортом тестера. Кроме того, не все модели тестеров позволяют измерять с хорошей точностью сигналы величиной десятки милливольт. В этом случае можно установить на клеммах усилителя выходной сигнал не 1, а 10 В. В режиме наших измерений усилитель нагружен на сопротивление более 100 Ом. Такая высокоомная нагрузка позволяет развить 10 В действующего напряжения даже большинству маломощных усилителей, причём без перегрева.
К сожалению, при 10 В на выходе есть опасность сжечь резистор цепи, обеспечивающей устойчивость, который присутствует в схемах многих усилителей. Поэтому не стоит проводить измерения на частотах выше 3 кГц.
Понятно, что в режиме «10 вольт» на пробном резисторе R2 надо установить не 40 мВ, а 400 мВ. Соответственно, шкала напряжения будет проградуирована от 125 мВ до 6000 мВ (6 В). При этом показания вольтметра делим на 100 и получаем величину импеданса АС. Например, 400 мВ соответствует 4 Ом.
(Продолжение в следующем номере)
ПрактикаAV #3/2002
И Н С Т Р У К Т И О Н С Этот калькулятор ultra отличается тем, что позволяет вам выбирать между 1) Вода течет со скоростью 36 дюймов в секунду и со скоростью 2) Вода течет по трубе диаметром 10 см со скоростью 9 литров в секунду.Какая скорость воды? 3) Вода течет по трубе диаметром 2 фута со скоростью 20 дюймов в секунду. Какая скорость потока? Для удобства чтения числа отображаются в формате «значащих цифр», поэтому вы можете |
Как рассчитать объем цилиндра в галлонах
Обновлено 5 декабря 2020 г.
Крис Дезил
Имперская система измерения может быть совершенно громоздкой, и ничто не иллюстрирует это больше, чем ее единица объема, галлон.Независимо от того, какие единицы вы используете для измерения размеров, у вас всегда есть дополнительный шаг после вычисления объема, если вы хотите получить ответ в галлонах. Объем цилиндра зависит от двух параметров: радиуса круглого сечения и длины. Измерьте их в дюймах или футах, и вы получите объем в кубических дюймах или кубических футах. Измерьте в метрических единицах, и вы получите объем в кубических метрах, литрах или миллилитрах. Во всех случаях необходимо умножить на коэффициент преобразования, чтобы получить объем в галлонах.2 ч} {4}
TL; DR (слишком долго; не читал)
Преобразуйте объем в галлоны, используя соответствующий коэффициент преобразования. 2 \ умножить на 60 = 1,696.3
Используя коэффициент преобразования 1 кубический дюйм = 0,004329 галлона США, вы получите объем как 7,34 галлона США.
Формула расхода
Расход жидкости — это мера объема жидкости, которая движется за определенный промежуток времени. Скорость потока зависит от площади трубы или канала, по которому движется жидкость, и скорости жидкости. Если жидкость течет по трубе, площадь равна A = πr 2 , где r — радиус трубы.Для прямоугольника площадь равна A = wh , где w — ширина, а h — высота. Расход может быть измерен в метрах в кубе в секунду ( м 3 / с ) или в литрах в секунду ( л / с ). Литры чаще используются для измерения объема жидкости, и 1 м 3 / с = 1000 л / с .
расход жидкости = площадь трубы или канала × скорость жидкости
Q = Av
Q = расход жидкости ( м 3 / с или л / с )
A = площадь трубы или канала ( м 2 )
v = скорость жидкости ( м / с )
Формула расхода Вопросы:
1) Вода течет по круглой трубе с радиусом 0.0800 м . Скорость воды 3,30 м / с . Какой расход воды в литрах в секунду ( л / с, )?
Ответ: Расход зависит от площади круглой трубы:
A = πr 2
A = π (0,0800 м) 2
A = π (0,00640 м 2 )
A = 0,0201 м 2
Площадь трубы 0,0201 м 2 .Расход можно найти в м 3 / с по формуле:
Q = Av
Q = (0,0201 м 2 ) (3,30 м / с)
Q = 0,0663 м 3 / с
Расход может быть преобразован в литры в секунду с помощью: 1 м 3 / с = 1000 л / с.
Q = 66,3 л / с
Расход воды по круглой трубе 66,3 л / с.
2) Вода стекает по открытому прямоугольному желобу. Желоб имеет ширину 1,20 м , глубина протекающей по нему воды 0,200 м . Скорость воды через круглую трубу имеет радиус 0,0800 м . Скорость воды 5,00 м / с . Какой расход воды через желоб в литрах в секунду ( л / с) ?
Ответ: Скорость потока зависит от площади желоба, через которую протекает вода:
A = wh
А = (1.20 м) (0,200 м )
A = 0,240 м 2
Площадь воды, протекающей по желобу, составляет 0,240 м 2 . Расход можно найти в м 3 / с по формуле:
Q = Av
Q = (0,240 м 2 ) (5,00 м / с)
Q = 1,20 м 3 / с
Расход можно преобразовать в литры в секунду с помощью:
1 м 3 / с = 1000 л / с.
Q = 1200 л / с
Расход воды в желобе 1200 л / с .
Расчет потерь на трение труб
Потоку жидкости через трубу препятствуют вязкие напряжения сдвига внутри жидкости и турбулентность, возникающая вдоль внутренней стенки трубы, которая зависит от шероховатости материала трубы.
Это сопротивление называется трением в трубе и обычно измеряется в футах или метрах напора жидкости, поэтому его также называют потерей напора из-за трения трубы.
Потеря напора в трубе
На протяжении многих лет было проведено большое количество исследований, направленных на создание различных формул, позволяющих рассчитать потерю напора в трубе. Большая часть этой работы была разработана на основе экспериментальных данных.
На общую потерю напора в трубе влияет ряд факторов, в том числе вязкость жидкости,
размер внутреннего диаметра трубы, внутренняя шероховатость внутренней поверхности трубы, изменение
высота между концами трубы и длина трубы, по которой движется жидкость.
Клапаны и фитинги на трубе также способствуют возникновению общих потерь напора, однако они должны быть рассчитаны отдельно от потерь на трение стенки трубы, используя метод моделирования потерь в фитингах труб с коэффициентами k.
Формула Дарси Вайсбаха
Формула Дарси или уравнение Дарси-Вайсбаха, как его обычно называют, теперь принята как наиболее точная формула потерь на трение в трубе, и, хотя ее труднее рассчитать и использовать, чем другие формулы потерь на трение, с появлением компьютеров она теперь стало стандартным уравнением для инженеров-гидротехников.2 / 2г)
где:
hf = потеря напора (м)
f = коэффициент трения
L = длина трубопровода (м)
d = внутренний диаметр трубопровода (м)
v = скорость жидкости (м / с)
g = ускорение свободного падения (м / с²)
или:
hf = потеря напора (фут)
f = коэффициент трения
L = длина трубопровода (футы)
d = внутренний диаметр трубопровода (футы)
v = скорость жидкости (фут / с)
g = ускорение свободного падения (фут / с²)
Однако установление коэффициентов трения все еще оставалось нерешенным, и это действительно была проблема, которую
потребовалась дальнейшая работа для разработки решения, такого как решение, полученное по формуле Коулбрука-Уайта и данных, представленных в диаграмме Moody.
Диаграмма Moody
Диаграмма Moody Chart, наконец, предоставила метод определения точного коэффициента трения, и это побудило использовать уравнение Дарси-Вайсбаха, которое быстро стало методом выбора для инженеров-гидротехников.
Внедрение персонального компьютера с 1980-х годов сократило время
требуется для расчета коэффициента трения и потери напора в трубе. Это само по себе расширило использование формулы Дарси-Вейсбаха до такой степени, что большинство других уравнений больше не используются.
Формула Хазена-Вильямса
До появления персональных компьютеров формула Хазена-Вильямса была чрезвычайно популярна среди инженеров по трубопроводам из-за ее относительно простых расчетных свойств.
Однако результаты Хазена-Вильямса основаны на значении коэффициента трения C hw, который используется в формуле, и значение C может значительно варьироваться, примерно от 80 до 130 и выше, в зависимости от материала трубы, размера трубы. и скорость жидкости.4,8655)
где:
hf = потеря напора в футах водяного столба
L = длина трубы в футах
C = коэффициент трения
галлонов в минуту = галлоны в минуту (галлоны США, а не британские галлоны)
d = внутренний диаметр трубы в дюймах
Эмпирический характер коэффициента трения C hw означает, что формула Хазена-Вильямса не подходит для точного прогнозирования потери напора. Результаты по потерям на трение действительны только для жидкостей с кинематической вязкостью 1.13 сантистоксов, при скорости потока менее 10 футов в секунду и при диаметре трубы более 2 дюймов.
Примечания: Вода при температуре 60 ° F (15,5 ° C) имеет кинематическую вязкость 1,13 сантистокс.
Общие значения коэффициента трения C hw, используемые для целей проектирования:
Асбестоцемент 140
Латунная трубка 130
Труба чугунная 100
Бетонная труба 110
Медная трубка 130
Гофрированная стальная труба 60
Труба оцинкованная 120
Стеклянная трубка 130
Свинцовый трубопровод 130
Пластиковая труба 140
Труба ПВХ 150
Трубы гладкие общего назначения 140
Труба стальная 120
Трубы стальные клепаные 100
Трубка чугунная, покрытая гудроном 100
Жестяная трубка 130
Деревянная клепка 110
Эти значения C hw обеспечивают некоторую поправку на изменения шероховатости внутренней поверхности трубы из-за точечной коррозии стенки трубы во время длительных периодов использования и накопления других отложений.
Интернет-курсы PDH. PDH для профессиональных инженеров. ПДХ Инжиниринг.
«Мне нравится широта ваших курсов по HVAC; не только экологичность или экономия энергии
курс. «
Russell Bailey, P.E.
Нью-Йорк
«Это укрепило мои текущие знания и научило меня еще нескольким новым вещам
, чтобы познакомить меня с новыми источниками
информации.»
Стивен Дедак, П.Е.
Нью-Джерси
«Материал был очень информативным и организованным. Я многому научился, и они были
.
очень быстро отвечает на вопросы.
Это было на высшем уровне. Будет использовать
снова. Спасибо. «
Blair Hayward, P.E.
Альберта, Канада
«Простой в использовании веб-сайт.Хорошо организовано. Я действительно буду снова пользоваться вашими услугами.
проеду по вашей роте
имя другим на работе «
Roy Pfleiderer, P.E.
Нью-Йорк
«Справочные материалы были превосходными, а курс был очень информативным, особенно с учетом того, что я думал, что уже знаком с вами.
с деталями Канзаса
Городская авария Хаятт.»
Майкл Морган, P.E.
Техас
«Мне очень нравится ваша бизнес-модель. Мне нравится просматривать текст перед покупкой. Я нашел класс
.
информативно и полезно
на моей работе »
Вильям Сенкевич, П.Е.
Флорида
«У вас большой выбор курсов, а статьи очень информативны.Вы
— лучшее, что я нашел ».
Russell Smith, P.E.
Пенсильвания
«Я считаю, что такой подход позволяет работающему инженеру легко зарабатывать PDH, давая время на просмотр.
материал. «
Jesus Sierra, P.E.
Калифорния
«Спасибо, что разрешили мне просмотреть неправильные ответы.На самом деле
человек узнает больше
от отказов »
John Scondras, P.E.
Пенсильвания
«Курс составлен хорошо, и использование тематических исследований является эффективным.
способ обучения. «
Джек Лундберг, P.E.
Висконсин
«Я очень впечатлен тем, как вы представляете курсы; i.е., позволяя
студент для ознакомления с курсом
материалов до оплаты и
получает викторину «
Арвин Свангер, П.Е.
Вирджиния
«Спасибо за то, что вы предложили все эти замечательные курсы. Я определенно выучил и
получил огромное удовольствие «
Мехди Рахими, П.Е.
Нью-Йорк
«Я очень доволен предлагаемыми курсами, качеством материалов и простотой поиска.
в режиме онлайн
курс.»
Уильям Валериоти, P.E.
Техас
«Этот материал в значительной степени оправдал мои ожидания. По курсу было легко следовать. Фотографии в основном обеспечивали хорошее наглядное представление о
обсуждаемых тем ».
Майкл Райан, P.E.
Пенсильвания
«Именно то, что я искал. Потребовался 1 балл по этике, и я нашел его здесь.»
Джеральд Нотт, П.Е.
Нью-Джерси
«Это был мой первый онлайн-опыт получения необходимых мне кредитов PDH. Это было
информативно, выгодно и экономично.
Я очень рекомендую
всем инженерам »
Джеймс Шурелл, П.Е.
Огайо
«Я понимаю, что вопросы относятся к« реальному миру »и имеют отношение к моей практике, и
не на основании какой-то непонятной секции
законов, которые не применяются
по «нормальная» практика.»
Марк Каноник, П.Е.
Нью-Йорк
«Отличный опыт! Я многому научился, чтобы использовать свой медицинский прибор.
« организация».
Иван Харлан, П.Е.
Теннесси
«Материалы курса имели хорошее содержание, не слишком математическое, с хорошим акцентом на практическое применение технологий».
Юджин Бойл, П.E.
Калифорния
«Это был очень приятный опыт. Тема была интересной и хорошо изложенной,
а онлайн-формат был очень
доступный и простой
использовать. Большое спасибо «.
Патрисия Адамс, P.E.
Канзас
«Отличный способ добиться соответствия требованиям PE Continuing Education в рамках ограничений по времени лицензиата.»
Joseph Frissora, P.E.
Нью-Джерси
«Должен признаться, я действительно многому научился. Помогает напечатанная викторина во время
обзор текстового материала. Я
также оценил просмотр
предоставлено фактических случаев »
Жаклин Брукс, П.Е.
Флорида
«Документ» Общие ошибки ADA при проектировании объектов «очень полезен.Модель
тест действительно потребовал исследования в
документ но ответы были
в наличии. «
Гарольд Катлер, П.Е.
Массачусетс
«Я эффективно использовал свое время. Спасибо за широкий выбор вариантов.
в транспортной инженерии, которая мне нужна
для выполнения требований
Сертификат ВОМ.»
Джозеф Гилрой, P.E.
Иллинойс
«Очень удобный и доступный способ заработать CEU для моих требований PG в Делавэре».
Ричард Роудс, P.E.
Мэриленд
«Я многому научился с защитным заземлением. Пока все курсы, которые я прошел, были отличными.
Надеюсь увидеть больше 40%
курс со скидкой.»
Кристина Николас, П.Е.
Нью-Йорк
«Только что сдал экзамен по радиологическим стандартам и с нетерпением жду возможности сдать дополнительные
курс. Процесс прост, и
намного эффективнее, чем
приходится путешествовать. «
Деннис Мейер, P.E.
Айдахо
«Услуги, предоставляемые CEDengineering, очень полезны для профессионалов
Инженеры получат блоки PDH
в любое время.Очень удобно ».
Пол Абелла, P.E.
Аризона
«Пока все отлично! Поскольку я постоянно работаю матерью двоих детей, у меня мало
время исследовать, где на
получить мои кредиты от. «
Кристен Фаррелл, П.Е.
Висконсин
«Это было очень познавательно и познавательно.Легко для понимания с иллюстрациями
и графики; определенно делает это
проще поглотить все
теории »
Виктор Окампо, P.Eng.
Альберта, Канада
«Хороший обзор принципов работы с полупроводниками. Мне понравилось пройти курс по
.
мой собственный темп во время моего утро
метро
на работу.»
Клиффорд Гринблатт, П.Е.
Мэриленд
«Просто найти интересные курсы, скачать документы и взять
викторина. Я бы очень рекомендовал
вам на любой PE, требующий
CE единиц. «
Марк Хардкасл, П.Е.
Миссури
«Очень хороший выбор тем из многих областей техники.»
Randall Dreiling, P.E.
Миссури
«Я заново узнал то, что забыл. Я также рад оказать финансовую помощь
по ваш промо-адрес который
пониженная цена
на 40%. «
Конрадо Казем, П.E.
Теннесси
«Отличный курс по разумной цене. Воспользуюсь вашими услугами в будущем».
Charles Fleischer, P.E.
Нью-Йорк
«Это был хороший тест и фактически подтвердил, что я прочитал профессиональную этику
кодов и Нью-Мексико
регламент. «
Брун Гильберт, П.E.
Калифорния
«Мне очень понравились занятия. Они стоили потраченного времени и усилий».
Дэвид Рейнольдс, P.E.
Канзас
«Очень доволен качеством тестовых документов. Буду использовать CEDengineerng
при необходимости дополнительных
Сертификация . «
Томас Каппеллин, П.E.
Иллинойс
«У меня истек срок действия курса, но вы все же выполнили свое обязательство и дали
мне то, за что я заплатил — много
оценено! «
Джефф Ханслик, P.E.
Оклахома
«CEDengineering предоставляет удобные, экономичные и актуальные курсы.
для инженера »
Майк Зайдл, П.E.
Небраска
«Курс был по разумной цене, а материал был кратким и
хорошо организовано. «
Glen Schwartz, P.E.
Нью-Джерси
«Вопросы подходили для уроков, а материал урока —
.
хороший справочный материал
для деревянного дизайна. «
Брайан Адамс, П.E.
Миннесота
«Отлично, я смог получить полезные рекомендации по простому телефонному звонку».
Роберт Велнер, P.E.
Нью-Йорк
«У меня был большой опыт работы в прибрежном строительстве — проектирование
Строительство курс и
очень рекомендую .»
Денис Солано, P.E.
Флорида
«Очень понятный, хорошо организованный веб-сайт. Материалы курса этики Нью-Джерси были очень хорошими
хорошо подготовлен. «
Юджин Брэкбилл, P.E.
Коннектикут
«Очень хороший опыт. Мне нравится возможность загружать учебные материалы на номер
.
обзор везде и
всякий раз, когда.»
Тим Чиддикс, P.E.
Колорадо
«Отлично! Поддерживайте широкий выбор тем на выбор».
Уильям Бараттино, P.E.
Вирджиния
«Процесс прямой, без всякой ерунды. Хороший опыт».
Тайрон Бааш, П.E.
Иллинойс
«Вопросы на экзамене были зондирующими и продемонстрировали понимание
материала. Полное
и всесторонний ».
Майкл Тобин, P.E.
Аризона
«Это мой второй курс, и мне понравилось то, что мне предложили этот курс
поможет по моей линии
работ.»
Рики Хефлин, П.Е.
Оклахома
«Очень быстро и легко ориентироваться. Я определенно буду использовать этот сайт снова».
Анджела Уотсон, П.Е.
Монтана
«Легко выполнить. Никакой путаницы при прохождении теста или записи сертификата».
Кеннет Пейдж, П.E.
Мэриленд
«Это был отличный источник информации о солнечном нагреве воды. Информативный
и отличный освежитель ».
Луан Мане, П.Е.
Conneticut
«Мне нравится подход к регистрации и возможность читать материалы в автономном режиме, а затем
вернуться, чтобы пройти викторину «
Алекс Млсна, П.E.
Индиана
«Я оценил объем информации, предоставленной для класса. Я знаю
это вся информация, которую я могу
использование в реальных жизненных ситуациях »
Натали Дерингер, P.E.
Южная Дакота
«Обзорные материалы и образец теста были достаточно подробными, чтобы я мог сделать
успешно завершено
курс.»
Ира Бродский, П.Е.
Нью-Джерси
«Веб-сайтом легко пользоваться, вы можете скачать материал для изучения, а потом вернуться
и пройдите викторину. Очень
удобно а на моем
собственный график «
Майкл Глэдд, P.E.
Грузия
«Спасибо за хорошие курсы на протяжении многих лет.»
Деннис Фундзак, П.Е.
Огайо
«Очень легко зарегистрироваться, получить доступ к курсу, пройти тест и распечатать PDH
Сертификат
. Спасибо за создание
процесс простой. »
Фред Шейбе, P.E.
Висконсин
«Опыт положительный.Быстро нашел курс, который соответствовал моим потребностям, и прошел
часовой PDH в
один час. «
Стив Торкильдсон, P.E.
Южная Каролина
«Мне понравилось загружать документы для проверки содержания
и пригодность, до
имея для оплаты
материал .»
Ричард Вимеленберг, P.E.
Мэриленд
«Это хорошее напоминание об ЭЭ для инженеров, не занимающихся электричеством».
Дуглас Стаффорд, П.Е.
Техас
«Всегда есть возможности для улучшения, но я ничего не могу придумать в вашем
процесс, требующий
улучшение.»
Thomas Stalcup, P.E.
Арканзас
«Мне очень нравится удобство участия в онлайн-викторине и получение сразу
сертификат . «
Марлен Делани, П.Е.
Иллинойс
«Учебные модули CEDengineering — это очень удобный способ доступа к информации по номеру
.
много различные технические зоны за пределами
по своей специализации без
надо ехать.»
Гектор Герреро, П.Е.
Грузия
Оценка количества краски для труб »Мир трубопроводной техники
Оценка количества краски
Пояснение
Требуемое количество краски для окраски трубы зависит от следующих факторов:
- Диаметр трубы.
- Длина трубы.
- Требуемая толщина сухой пленки (ТСП).
- Процент содержания твердых веществ в данной краске.
- Потери краски во время покраски в зависимости от используемого метода покраски.
Толщина влажной краски
Когда краска наносится на трубу, она находится во влажном состоянии с летучими органическими соединениями. Когда он высыхает, все летучие компоненты уходят, оставляя только твердые частицы. Таким образом, для достижения определенной толщины сухой пленки требуется более высокая толщина влажной пленки, которая рассчитывается как:
Толщина мокрой пленки (WFT) = DFT / Доля твердых частиц.
Теоретическое количество краски
Теоретическое количество краски рассчитывается путем умножения общей площади окрашиваемой поверхности на толщину мокрой пленки.
Теоретическое количество краски = Площадь поверхности X WFT.
Wastage
В процессе окраски некоторое количество краски расходуется впустую, что зависит от метода нанесения краски. Типичные проценты потерь:
- Кисть или валик: 10%.
- Безвоздушное распыление: 20%.
- Обычная окраска распылением: 30%
Итак, мы должны добавить потери к расчетному количеству краски, чтобы получить фактическое количество краски.
Фактическое количество краски = теоретическое количество краски / доля твердых веществ в краске.
Пример расчета
Труба с номинальным диаметром трубы 10 дюймов должна быть окрашена неорганическим цинкосиликатным покрытием с процентным содержанием твердых частиц 60%. Требуемая толщина сухой пленки 70 мкм. Способ нанесения — обычная окраска распылением. Рассчитайте необходимое количество краски для длины 100 метров.
- Диаметр трубы в мм (D) = 10 ″ X 25,4 = 254 мм.
- Длина трубы (L) = 100 метров = 100000 мм.
- Площадь поверхности трубы на один метр (A) = Pi X D = 3.141 Х 254 = 0,797814 кв. ММ. (Нет необходимости брать фактический наружный диаметр трубы из таблиц данных по трубам. Разница незначительна.)
- Общая площадь поверхности = A X L = 797,814 X 10000 0 = 79781400 Кв.м.
- Требуемая толщина сухой пленки (DFT) = 70 мкм = 0,07 мм.
- Доля твердых веществ в краске (S) = Процент твердых веществ / 100 = 60/100 = 0,6
- Толщина пленки Welt (WFT) = (DFT / S) = 0,07 / 0,6 = 0,1167 мм.
- Теоретический необходимый объем краски = Общая площадь поверхности X WFT = 79781400 X 0.1167 = 89 Куб. Мм. = 9,3 · 10489 литров.
- При использовании обычного метода окраски распылением потери составляют около 30%. Таким образом, для фактической окраски используется только 70% краски. Таким образом, фактически необходимое количество краски — это теоретическое количество краски, деленное на долю фактического использования краски.
- Фактический объем краски = теоретический объем краски / 0,7 = 9,3 · 10489 / 0,7 = 13,3 литра.
Нравится:
Нравится Загрузка …
Справка по тесту: Fluid Flow | EZ-pdh.com
Используйте поиск, чтобы быстро найти ответы на вопросы — откройте окно поиска (ctrl + f), затем введите ключевое слово из вопроса, чтобы перейти к этим терминам в материалах курса
Введение
Поток жидкости — важная часть большинства промышленных процессов; особенно те, которые связаны с передачей тепла.Часто, когда требуется отвести тепло из точки, в которой оно генерируется, в процессе теплопередачи участвует какой-либо тип жидкости. Примерами этого являются охлаждающая вода, циркулирующая через бензиновый или дизельный двигатель, поток воздуха, проходящий через обмотки двигателя, и поток воды через активную зону ядерного реактора. Системы подачи жидкости также обычно используются для смазки.
Течение жидкости в ядерной области может быть сложным и не всегда подлежит строгому математическому анализу.В отличие от твердых тел, частицы жидкости движутся по трубопроводу и компонентам с разной скоростью и часто подвергаются разным ускорениям.
Несмотря на то, что подробный анализ потока жидкости может быть чрезвычайно трудным, основные концепции, связанные с проблемами потока жидкости, довольно просты. Эти базовые концепции могут быть применены при решении проблем потока жидкости путем использования упрощающих допущений и средних значений, где это необходимо. Несмотря на то, что такого типа анализа будет недостаточно для инженерного проектирования систем, он очень полезен для понимания работы систем и прогнозирования приблизительной реакции жидкостных систем на изменения рабочих параметров.
Основные принципы потока жидкости включают три концепции или принципа; первые два из которых студент изучал в предыдущих руководствах. Первый — это принцип количества движения (приводящий к уравнениям сил жидкости), который был рассмотрен в руководстве по классической физике. Второй — это сохранение энергии (ведущее к первому закону термодинамики), которое изучалось в термодинамике. Третий — это сохранение массы (приводящее к уравнению неразрывности), которое будет объяснено в этом модуле.
Свойства жидкостей
Жидкость — это любое вещество, которое течет, потому что его частицы не прикреплены друг к другу жестко. Сюда входят жидкости, газы и даже некоторые материалы, которые обычно считаются твердыми телами, например стекло. По сути, жидкости — это материалы, которые не имеют повторяющейся кристаллической структуры.
Некоторые свойства жидкостей обсуждались в разделе «Термодинамика» этого текста. К ним относятся температура, давление, масса, удельный объем и плотность. Температура была определена как относительная мера того, насколько горячий или холодный материал. Его можно использовать для прогнозирования направления передачи тепла. Давление было определено как сила на единицу площади. Обычными единицами измерения давления являются фунты силы на квадратный дюйм (psi). Масса определяется как количество вещества, содержащегося в теле, и его следует отличать от веса, который измеряется силой тяжести на теле. Удельный объем вещества — это объем на единицу массы вещества.Стандартные единицы измерения — фут 3 / фунт. Плотность — это масса вещества на единицу объема. Типичные единицы — фунт / фут 3 . Плотность и удельный объем противоположны друг другу. И плотность, и удельный объем зависят от температуры и в некоторой степени от давления жидкости. По мере увеличения температуры жидкости плотность уменьшается, а удельный объем увеличивается. Поскольку жидкости считаются несжимаемыми, увеличение давления не приведет к изменению плотности или удельного объема жидкости.На самом деле жидкости можно слегка сжимать при высоких давлениях, что приводит к небольшому увеличению плотности и небольшому уменьшению удельного объема жидкости.
Плавучесть
Плавучесть определяется как тенденция тела плавать или подниматься при погружении в жидкость. У всех нас было множество возможностей наблюдать плавучие эффекты жидкости. Когда мы идем плавать, наши тела почти полностью поддерживаются водой. Дерево, лед и пробка плавают на воде.Когда мы поднимаем камень с русла ручья, он внезапно кажется тяжелее, выходя из воды. Лодки полагаются на эту плавучую силу, чтобы оставаться на плаву. Величина этого плавучего эффекта была впервые вычислена и указана греческим философом Архимедом. Когда тело помещается в жидкость, оно поддерживается силой, равной весу вытесняемой им воды.
Если тело весит больше, чем жидкость, которую оно вытесняет, оно тонет, но будет казаться, что теряет количество, равное весу вытесненной жидкости, как наша скала.Если тело весит меньше, чем вес вытесненной жидкости, тело поднимется на поверхность, в конце концов, плавая на такой глубине, которая вытеснит объем жидкости, вес которой будет равен ее собственному весу. Плавающее тело вытесняет текучую среду, в которой оно плавает, под собственным весом.
Сжимаемость
Сжимаемость — это мера изменения объема, которому подвергается вещество, когда на вещество оказывается давление. Жидкости обычно считаются несжимаемыми.Например, давление 16 400 фунтов на квадратный дюйм приведет к уменьшению данного объема воды только на 5% от его объема при атмосферном давлении. С другой стороны, газы очень сжимаются. Объем газа можно легко изменить, оказав на газ внешнее давление. несколько футов заметно больше атмосферного давления.Тщательные измерения показывают, что давление жидкости прямо пропорционально глубине, и для данной глубины жидкость оказывает одинаковое давление во всех направлениях.
Рисунок 1: Давление в зависимости от глубины
Как показано на Рисунке 1, давление на разных уровнях в резервуаре меняется, и это заставляет жидкость покидать резервуар с разными скоростями. Давление определялось как сила на единицу площади. В случае этого резервуара сила обусловлена весом воды выше точки, в которой определяется давление.
Давление = Сила / Площадь
= Вес / Площадь
P = (мг) / (A g c )
= (ρ V g) / (A g c )
Где:
m = масса в фунтах
g = ускорение свободного падения 32,17 фут / сек 2
г c = 32 фунт-фут / фунт-сила-сек 2
A = площадь в футах 2
V = объем в футах 3
ρ = плотность жидкости в фунтах / фут 3
Объем равен площади поперечного сечения, умноженной на высоту (h) жидкости.Подставляя это в приведенное выше уравнение, получаем:
P = (ρ A hg) / (A g c )
P = (ρ hg) / (g c )
Это уравнение говорит нам, что давление оказываемое водяным столбом прямо пропорционально высоте столба и плотности воды и не зависит от площади поперечного сечения столба. Давление на тридцать футов ниже поверхности стояка диаметром один дюйм такое же, как давление на тридцать футов ниже поверхности большого озера.
Пример 1:
Если резервуар на Рисунке 1 заполнен водой с плотностью 62,4 фунта / фут3, рассчитайте давление на глубинах 10, 20 и 30 футов.
Решение:
P = (ρhg) / g c
P 10 футов = (62,4 фунт / фут 3 ) (1 фут) (32,17 фут / сек 2 / (32,17 фунт-м- фут / фунт-сила / дюйм 2 )
= 624 фунт-сила / фут 2 (1 фут 2 /144 дюйм 2 )
= 4,33 фунт-силы / дюйм 2
P 20 = ( 624 фунт / фут 3 ) (20 футов) (32.17 фут / сек 2 /( 32,17 фунт-фут / фунт-сила-сек 2 )
= 1248 фунт-сила / фут 2 (1 фут 2 /144 дюйм 2 )
= 8,67 фунт-фут / дюйм
P 30 футов = (62,4 фунт / фут3) (30 футов) (32,17 фут / сек 2 / 32,17 фунт-фут / фунт-сила-сек 2 )
= 1872 фунт-сила / фут 2 (1 футов 2 /144 дюйм 2 )
= 13,00 фунт-сила / дюйм 2
Пример 2:
Цилиндрический резервуар для воды высотой 40 футов и диаметром 20 футов заполнен водой с плотностью из 61.9 фунт / фут 3 .
(а) Какое давление воды на дне резервуара?
(b) Какая средняя сила действует на дно?
Решение:
(a) P = (phg) / g c
P = (61,9 фунт / фут 3 ) (40 футов) (32,17 фут / сек 2 / 32,17 фунт-фут / фунт-сила-сек 2 )
= 2476 фунт-сила / фут 2 (1 фут 2 /144 дюйм 2 )
= 17,2 фунт-сила / дюйм 2
(b) Давление = сила / площадь
Сила = (Давление) (Площадь)
Площадь = πr 2
F = (17.2 фунта-силы / дюйм 2 ) π (10 футов) 2 (144 дюйма 2 /1 фут 2 )
= 7,78 x 10 5 фунт-сила
Закон Паскаля
Давление жидкостей в каждом из ранее упомянутых случаев было связано с весом жидкости. Давление жидкости также может быть результатом приложения внешних сил к жидкости. Рассмотрим следующие примеры. На рисунке 2 изображен контейнер, полностью заполненный жидкостью. A, B, C, D и E представляют собой поршни одинаковой площади поперечного сечения, вставленные в стенки резервуара.На поршни C, D и E будут действовать силы из-за давления, вызванного разной глубиной жидкости. Предположим, что силы, действующие на поршни из-за давления, вызванного весом жидкости, следующие: A = 0 фунтов-силы, B = 0 фунтов-силы, C = 10 фунтов-силы, D = 30 фунтов-силы и E = 25 фунтов-силы. Теперь позвольте приложить к поршню А внешнюю силу в 50 фунтов-силы. Эта внешняя сила вызовет повышение давления во всех точках контейнера на такую же величину. Поскольку все поршни имеют одинаковую площадь поперечного сечения, увеличение давления приведет к тому, что силы, действующие на поршни, увеличатся на 50 фунтов-силы.Таким образом, если к поршню A приложена внешняя сила в 50 фунтов-силы, сила, оказываемая жидкостью на другие поршни, теперь будет следующей: B = 50 фунтов-силы, C = 60 фунтов-силы, D = 80 фунтов-силы и E = 75 фунтов-силы. . »
Этот эффект внешней силы на замкнутый флюид был впервые заявлен Паскалем в 1653 году.
Давление, приложенное к замкнутому флюиду, передается в неизменном виде через ограничивающий сосуд системы.
Рисунок 2: Закон Паскаля
Контрольный объем
В термодинамике контрольный объем был определен как фиксированная область в пространстве, где изучаются массы и энергии, пересекающие границы области.Эта концепция контрольного объема также очень полезна при анализе проблем с потоком жидкости. Граница контрольного объема для потока жидкости обычно принимается за физическую границу части, через которую протекает поток. Концепция контрольного объема используется в приложениях гидродинамики с использованием принципов непрерывности, импульса и энергии, упомянутых в начале этой главы. После того, как контрольный объем и его граница установлены, различные формы энергии, пересекающие границу с жидкостью, могут быть рассмотрены в форме уравнения для решения проблемы жидкости.Поскольку в задачах потока жидкости обычно рассматривается жидкость, пересекающая границы контрольного объема, подход с контрольным объемом называется «открытым» системным анализом, который аналогичен концепциям, изучаемым в термодинамике. В ядерной области есть особые случаи, когда жидкость не пересекает контрольную границу. Подобные случаи изучаются с использованием «закрытого» системного подхода.
Независимо от природы потока, все ситуации, связанные с потоком, подчиняются установленным основным законам природы, которые инженеры выразили в форме уравнений.Сохранение массы и сохранение энергии всегда выполняются в задачах с жидкостью, наряду с законами движения Ньютона. Кроме того, каждая задача будет иметь физические ограничения, называемые математически граничными условиями, которые должны быть выполнены, прежде чем решение проблемы будет согласовано с физическими результатами.
Объемный расход
Объемный расход расход скорость (V˙) системы — это мера объема жидкости, проходящей через точку в системе за единицу времени.Объемный расход можно рассчитать как произведение площади поперечного сечения (A) потока и средней скорости потока (v).
V˙ = A v (3-1)
Если площадь измеряется в квадратных футах, а скорость — в футах в секунду, уравнение 3-1 приводит к объемному расходу, измеренному в кубических футах в секунду. Другие распространенные единицы объемного расхода включают галлоны в минуту, кубические сантиметры в секунду, литры в минуту и галлоны в час.
Пример:
Труба с внутренним диаметром 4 дюйма содержит воду, которая течет со средней скоростью 14 футов в секунду.Рассчитайте объемный расход воды в трубе.
Решение:
Используйте уравнение 3-1 и замените площадь.
V˙ = (π r 2) v
V˙ = (3,14) (2/12 футов) 2 (14 футов / сек)
V˙ = 1,22 футов 3 / сек
Масса Расход
Массовый расход (м²) системы — это мера массы жидкости, проходящей через точку в системе за единицу времени. Массовый расход связан с объемным расходом, как показано в уравнении 3-2, где ρ — плотность жидкости.
m˙ = ρV˙ (3-2)
Если объемный расход выражен в кубических футах в секунду, а плотность выражена в фунтах массы на кубический фут, уравнение 3-2 приводит к массовому расходу, измеренному в фунтах- масса в секунду. Другие распространенные единицы измерения массового расхода включают килограммы в секунду и фунты массы в час.
Замена V˙ в уравнении 3-2 соответствующими членами из уравнения 3-1 позволяет напрямую рассчитать массовый расход.
m˙ = ρ A v (3-3)
Пример:
Вода в трубе из предыдущего примера имела плотность 62.44 фунт / фут3. Рассчитайте массовый расход.
Решение:
м˙ = ρ V˙
м˙ = (62,44 фунт / фут 3 ) (1,22 фута 3 / сек)
м˙ = 76,2 фунт / сек
Сохранение массы
В термодинамике вы узнали, что энергия не может быть ни создана, ни уничтожена, а только изменена по форме. То же самое и с массой. Сохранение массы — это инженерный принцип, который гласит, что все массовые расходы в контрольном объеме равны всем массовым расходам из контрольного объема плюс скорость изменения массы в контрольном объеме.Математически этот принцип выражается уравнением 3-4.
m˙
дюйм = m˙ out + ∆m / ∆t (3-4)
где:
∆m / ∆t = увеличение или уменьшение массы в пределах контрольного объема в течение ( заданный период времени)
Устойчивый поток
Устойчивый поток относится к состоянию, при котором свойства жидкости в любой отдельной точке системы не меняются с течением времени. Эти свойства жидкости включают температуру, давление и скорость.Одним из наиболее важных свойств, которое является постоянным в системе с установившимся потоком, является массовый расход системы. Это означает, что в каком-либо компоненте системы не происходит накопления массы.
Уравнение неразрывности
Уравнение неразрывности — это просто математическое выражение принципа сохранения массы. Для контрольного объема, который имеет один вход и один выход, принцип сохранения массы гласит, что для установившегося потока массовый расход в объеме должен равняться массовому расходу на выходе.Уравнение неразрывности для этой ситуации выражается уравнением 3-5.
м˙
вход = м˙ выход (3-5)
(ρAv) вход = (ρAv) выход
Для контрольного объема с несколькими входами и выходами принцип сохранения масса требует, чтобы сумма массовых расходов в контрольном объеме была равна сумме массовых расходов из контрольного объема. Уравнение неразрывности для этой более общей ситуации выражается уравнением 3-6.
∑ м˙
входов = м˙ выходов (3-6)
Одним из простейших приложений уравнения неразрывности является определение изменения скорости жидкости
из-за расширения или сжатия диаметра трубка.
Пример: уравнение непрерывности — расширение трубопровода
Установившийся поток существует в трубе, которая постепенно расширяется с диаметра 6 дюймов до диаметра 8 дюймов. Плотность жидкости в трубе постоянна и равна 60 .8 фунт / фут3. Если скорость потока составляет 22,4 фута / сек в секции 6 дюймов, какова скорость потока в секции 8 дюймов?
Решение:
Из уравнения неразрывности мы знаем, что массовый расход в секции 6 дюймов должен равняться массовому расходу в секции 8 дюймов. Пусть нижний индекс 1 представляет 6-дюймовую секцию, а 2 — 8-дюймовую секцию, мы получаем следующее.
m˙ 1 = m˙ 2
ρ 1 A 1 v 1 = ρ 2 A 2 v 2
v 2 = v (ρ 1/ ρ 2 ) (A 1 / A 2 )
v 2 = v 1 (π / r 1 2 ) (π / r 2 2 )
v 2 = (22.4 фута / сек) [(3 дюйма) 2 / (4 дюйма) 2 ]
v 2 = 12,6 фута / сек
Таким образом, используя уравнение неразрывности, мы увеличиваем диаметр трубы от От 6 до 8 дюймов скорость потока снизилась с 22,4 до 12,6 футов / сек.
Уравнение неразрывности также можно использовать, чтобы показать, что уменьшение диаметра трубы приведет к увеличению скорости потока.
Пример: уравнение непрерывности — центробежный насос Рисунок 3: Уравнение непрерывности
Входной диаметр насоса охлаждающей жидкости реактора, показанный на рисунке 3, составляет 28 дюймов.в то время как поток на выходе через насос составляет 9200 фунтов / м3. Плотность воды составляет 49 фунтов на кубический метр. Какая скорость на входе в насос?
Решение:
Вход = πr 2 = (3,13) (14 дюймов ((1 фут / 12 дюймов)) 2
= 4,28 фута 2
м˙ вход = м ˙ на выходе = 9200 фунтов / с
(ρAv) на входе = 9200 фунтов / с
на входе = 9200 фунтов / с / Aρ
= (9200 фунтов / с) / [(4.28 футов 2) (49 фунтов / фут 3 )]
v на входе = 43,9 футов / сек
В приведенном выше примере показано, что скорость потока в систему такая же, как и вне системы. Та же самая концепция верна, даже если более одного пути потока могут входить или выходить из системы одновременно. Баланс массы просто регулируется, чтобы указать, что сумма всех потоков, входящих в систему, равна сумме всех потоков, покидающих систему, если существуют установившиеся условия. Пример этого физического случая включен в следующий пример.
Пример: уравнение непрерывности — несколько выходов Рисунок 4: Y-образная конфигурация для примера задачи
Трубопроводная система имеет Y-образную конфигурацию для разделения потока, как показано на рисунке 4. Диаметр входной ветви составляет 12 дюймов, а диаметры выпускных колен составляют 8 и 10 дюймов. Скорость в 10-дюймовых опорах составляет 10 футов / сек. Поток через основную часть составляет 500 фунтов / м3. Плотность воды 62,4 фунта / фут3. Какова скорость на участке трубы диаметром 8 дюймов?
Решение:
A 8 = π [4 дюйм.(1 фут / 12 дюймов)] 2
= 0,349 фута 2
A 10 = π [5 дюймов (1 фут / 12 дюймов)] 2
= 0,545 фута 2
Σm˙ входов = Σm˙ выходов
м˙ 12 = m˙ 10 + m˙ 8
м˙ 8 = m˙ 12 — m˙ 10
(ρAv) 8 = m˙ 12 — (ρAv) 10
v 8 = (m˙ 12 — (ρAv) 10 ) / (ρA) 8
= [(500 фунт / сек) — (62.4 фунта / фут3) (0,545 фут2) (10 фут / сек)] / (62,4 фунта / фут3) (0,349 фут 2 )
v 8 = 7,3 фут / сек
Основные положения данной главы кратко изложены на следующей странице.
- Изменения плотности жидкости обратно пропорциональны изменениям температуры.
- Плавучесть — это тенденция тела плавать или подниматься при погружении в жидкость.
- Давление , оказываемое водяным столбом, прямо пропорционально высоте столба и плотности воды.
P = ρ h г / г c
- Закон Паскаля гласит, что давление, приложенное к замкнутой жидкости, передается в неизменном виде по замкнутому сосуду системы.
- Объемный расход — это объем жидкости в единицу времени, проходящий через точку в жидкостной системе.
- Массовый расход — это масса жидкости в единицу времени, проходящая через точку в жидкостной системе.
- Объемный расход рассчитывается как произведение средней скорости жидкости и площади поперечного сечения потока.
V˙ = A v
- Массовый расход рассчитывается как произведение объемного расхода и плотности жидкости.
m˙ = ρ A v
- Принцип сохранения массы гласит, что все массовые расходы в контрольном объеме равны всем массовым расходам из контрольного объема плюс скорость изменения масса в контрольном объеме.
- Для контрольного объема с одним входом и выходом уравнение неразрывности может быть выражено следующим образом:
м˙ вход = м˙ выход
- Для контрольного объема с несколькими входами и выходов уравнение непрерывности:
m входов = m выходов
Режимы потока
Весь поток жидкости классифицируется по одной из двух широких категорий или режимов.Эти два режима потока — ламинарный поток и турбулентный поток. Режим потока, будь то ламинарный или турбулентный, важен при проектировании и работе любой жидкостной системы. Величина гидравлического трения, которая определяет количество энергии, необходимое для поддержания желаемого потока, зависит от режима потока. Это также важно для некоторых приложений, связанных с передачей тепла жидкости.
Ламинарный поток
Ламинарный поток также называют обтекаемым или вязким потоком.Эти термины описывают поток, потому что в ламинарном потоке (1) слои воды текут друг над другом с разными скоростями практически без перемешивания между слоями, (2) частицы жидкости движутся по определенным и наблюдаемым траекториям или линиям тока и (3) ) течение характерно для вязкой (густой) жидкости или является тем потоком, в котором вязкость жидкости играет значительную роль.
Турбулентный поток
Турбулентный поток характеризуется неравномерным движением частиц жидкости. Нет определенной частоты, как в волновом движении.Частицы движутся по неправильным путям, без видимого рисунка и определенных слоев.
Профили скорости потока
Не все частицы жидкости движутся по трубе с одинаковой скоростью. Форма кривой скорости (профиль скорости на любом заданном участке трубы) зависит от того, является ли поток ламинарным или турбулентным. Если поток в трубе ламинарный, распределение скорости в поперечном сечении будет параболическим по форме с максимальной скоростью в центре, примерно вдвое превышающей среднюю скорость в трубе.В турбулентном потоке существует довольно равномерное распределение скорости по сечению трубы, в результате чего вся жидкость течет с заданным единственным значением. Рисунок 5 помогает проиллюстрировать изложенные выше идеи. Скорость жидкости, контактирующей со стенкой трубы, по существу равна нулю и увеличивается по мере удаления от стенки.
Рисунок 5: Профили скорости ламинарного и турбулентного потока
Обратите внимание на рисунок 5, что профиль скорости зависит от состояния поверхности стенки трубы. Более гладкая стенка дает более равномерный профиль скорости, чем грубая стенка трубы.
Средняя (объемная) скорость
Во многих задачах потока жидкости вместо определения точных скоростей в разных местах в одном и том же поперечном сечении потока достаточно позволить одной средней скорости представлять скорость всей жидкости в этой точке в трубе. Это довольно просто для турбулентного потока, поскольку профиль скорости плоский по большей части поперечного сечения трубы. Разумно предположить, что средняя скорость равна скорости в центре трубы.
Если режим потока ламинарный (профиль скорости параболический), все еще существует проблема попытки представить «среднюю» скорость в любом заданном поперечном сечении, поскольку среднее значение используется в уравнениях потока жидкости. Технически это делается с помощью интегрального исчисления. На практике ученик должен использовать среднее значение, равное половине значения средней линии.
Вязкость
Вязкость — это свойство жидкости, которое измеряет сопротивление жидкости деформации из-за силы сдвига.Вязкость — это внутреннее трение жидкости, которое заставляет ее сопротивляться протеканию мимо твердой поверхности или других слоев жидкости. Вязкость также можно рассматривать как меру сопротивления жидкости течению. Густое масло имеет высокую вязкость; вода имеет низкую вязкость. Единица измерения абсолютной вязкости:
µ = абсолютная вязкость жидкости (фунт-сила-сек / фут2).
Вязкость жидкости обычно существенно зависит от температуры жидкости и относительно не зависит от давления.Для большинства жидкостей, когда температура жидкости увеличивается, вязкость жидкости уменьшается. Пример этого можно увидеть в смазочном масле двигателей. Когда двигатель и его смазочное масло холодные, масло очень вязкое или густое. После запуска двигателя и повышения температуры смазочного масла вязкость масла значительно снижается, и масло кажется намного более жидким.
Идеальная жидкость
Идеальная жидкость — это жидкость, которая не сжимается и не имеет вязкости.Идеальных жидкостей на самом деле не существует, но иногда полезно рассмотреть, что случилось бы с идеальной жидкостью в конкретной задаче потока жидкости, чтобы упростить задачу.
Число Рейнольдса
Режим потока (ламинарный или турбулентный) определяется путем оценки числа Рейнольдса потока (см. Рисунок 5). Число Рейнольдса, основанное на исследованиях Осборна Рейнольдса, представляет собой безразмерное число, состоящее из физических характеристик потока. Уравнение 3-7 используется для расчета числа Рейнольдса (N R ) для потока жидкости.
N
R = PvD / мкг c (3-7)
где:
N R = число Рейнольдса (без единицы измерения)
v = средняя скорость (фут / сек)
D = диаметр трубы (футы)
µ = абсолютная вязкость жидкости (фунт-сила-сек / фут2)
ρ = массовая плотность жидкости (фунт / фут3)
г c = гравитационная постоянная (32,2 фут-фунт-сила / фунт-сила-сек2) )
Для практических целей, если число Рейнольдса меньше 2000, поток является ламинарным.Если оно больше 3500, поток турбулентный. Потоки с числами Рейнольдса от 2000 до 3500 иногда называют переходными. Большинство жидкостных систем на ядерных установках работают с турбулентным потоком. Числа Рейнольдса можно удобно определить с помощью диаграммы Moody Chart; пример которого приведен в Приложении B. Дополнительные сведения об использовании диаграммы Moody Chart представлены в последующем тексте.
Основные положения этой главы кратко изложены ниже.
• Ламинарный поток Слои воды текут друг над другом с разной скоростью, практически без перемешивания между слоями.Профиль скорости потока для ламинарного потока в круглых трубах имеет параболическую форму с максимальным потоком в центре трубы и минимальным потоком на стенках трубы. Средняя скорость потока составляет примерно половину максимальной скорости.
• Турбулентный поток Поток характеризуется неравномерным движением частиц жидкости. Профиль скорости турбулентного потока довольно плоский в центральной части трубы и быстро падает очень близко к стенкам.Средняя скорость потока примерно равна скорости в центре трубы.
• Вязкость — это свойство жидкости, которое измеряет сопротивление жидкости деформации из-за силы сдвига. Для большинства жидкостей температура и вязкость обратно пропорциональны.
• Идеальная жидкость — это несжимаемая жидкость без вязкости.
• Увеличение числа Рейнольдса указывает на усиление турбулентности потока.
Общее уравнение энергии
Принцип сохранения энергии гласит, что энергия не может быть ни создана, ни разрушена.Это эквивалентно Первому закону термодинамики, который использовался для разработки общего уравнения энергии в модуле по термодинамике. Уравнение 3-8 представляет собой формулировку общего уравнения энергии для открытой системы.
Q + (U + PE + KE + PV) дюйм =
W + (U + PE + KE + PV)
выход + (U + PE + KE + PV) сохраненный (3-8 )
где:
Q = тепло (БТЕ)
U = внутренняя энергия (БТЕ)
PE = потенциальная энергия (фут-фунт-сила)
KE = кинетическая энергия (фут-фунт-сила)
P = давление ( фунт-сила / фут 2 )
V = объем (фут 3 )
W = работа (фут-фунт-сила)
Упрощенное уравнение Бернулли
Уравнение Бернулли является результатом применения общего уравнения энергии и первого закона термодинамики к системе с установившимся потоком, в которой никакая работа не выполняется с жидкостью или ею, не передается тепло к или от жидкости, и не происходит никаких изменений внутренней энергии (т.е., без изменения температуры) жидкости. В этих условиях общее уравнение энергии упрощается до уравнения 3-9.
(PE + KE + PV)
1 = (PE + KE + PV) 2 (3-9)
Подставляя соответствующие выражения для потенциальной энергии и кинетической энергии, уравнение 3-9 можно переписать как Equation 3-10.
mgz
1/ g c + mv 1 2/ 2g c + P 1 V 1 = mgz 920 + 920 936 g20 920 mv 2 2/ 2g c + P 2 V 2 (3-10)
где:
m = масса (фунт-метр)
z = высота над ссылка (фут)
v = средняя скорость (фут / сек)
g = ускорение свободного падения (32.17 фут / сек 2 )
gc = гравитационная постоянная, (32,17 фут-фунт / фунт-сила-сек 2 )
Примечание: коэффициент g c требуется только при использовании английской системы измерения и Масса измеряется в фунтах массы. По сути, это коэффициент преобразования, необходимый для непосредственного вывода единиц измерения. Нет необходимости в множителе, если масса измеряется в пробках или если используется метрическая система измерения.
Каждый член в уравнении 3-10 представляет форму энергии, которой обладает движущаяся жидкость (потенциальная, кинетическая энергия и энергия, связанная с давлением).По сути, уравнение физически представляет собой баланс энергий KE, PE, PV, так что если одна форма энергии увеличивается, одна или несколько других уменьшаются, чтобы компенсировать, и наоборот.
Умножение всех членов в уравнении 3-10 на коэффициент gc / mg дает форму уравнения Бернулли, показанного уравнением 3-11.
z
1 + v 1 2 / 2g + P 1 ν 1 g c / g = z 2 + v 2 2 / 2g + P 2 ν 2 г c / г (3-11)
Напор
Поскольку единицы для всех различных форм энергии в уравнении 3-11 измеряются в единицах расстояния, эти термины иногда называют «Напоры» (напор, напор скорости и напор).Термин «напор» используется инженерами применительно к давлению. Это ссылка на высоту, обычно в футах, водяного столба, который будет выдерживать данное давление. Каждую из энергий, которыми обладает жидкость, можно выразить через голову. Высота напора представляет собой потенциальную энергию жидкости из-за ее возвышения над контрольным уровнем. Скоростной напор представляет собой кинетическую энергию жидкости. Это высота в футах, на которую текущая жидкость поднялась бы в столбе, если бы вся ее кинетическая энергия была преобразована в потенциальную.Напор представляет собой энергию потока столба жидкости, вес которой эквивалентен давлению жидкости.
Сумма подъемного напора, скоростного напора и напора жидкости называется общим напором. Таким образом, уравнение Бернулли утверждает, что общий напор жидкости постоянен.
Преобразование энергии в жидкостных системах
Уравнение Бернулли позволяет легко исследовать, как происходит передача энергии между подъемным напором, скоростным напором и напором.Можно исследовать отдельные компоненты трубопроводных систем и определить, какие свойства жидкости изменяются и как это влияет на энергетический баланс.
Если труба, содержащая идеальную жидкость, подвергается постепенному расширению в диаметре, уравнение неразрывности говорит нам, что по мере увеличения диаметра и площади проходного сечения скорость потока должна уменьшаться, чтобы поддерживать тот же массовый расход. Поскольку скорость на выходе меньше скорости на входе, скоростной напор потока должен уменьшаться от входа к выходу.Если труба лежит горизонтально, напор не меняется; следовательно, уменьшение скоростного напора должно быть компенсировано увеличением напора. Поскольку мы рассматриваем идеальную несжимаемую жидкость, удельный объем жидкости не изменится. Единственный способ увеличения напора несжимаемой жидкости — это увеличение давления. Таким образом, уравнение Бернулли показывает, что уменьшение скорости потока в горизонтальной трубе приведет к увеличению давления.
Если труба постоянного диаметра, содержащая идеальную жидкость, подвергается уменьшению отметки, результат будет таким же, но по разным причинам. В этом случае скорость потока и скоростной напор должны быть постоянными, чтобы удовлетворять уравнению неразрывности массы.
Таким образом, уменьшение напора можно компенсировать только увеличением напора. Опять же, жидкость несжимаема, поэтому увеличение напора должно приводить к увеличению давления.
Хотя уравнение Бернулли имеет несколько ограничений, наложенных на него, существует множество задач с физической жидкостью, к которым оно применяется.Как и в случае сохранения массы, уравнение Бернулли может применяться к задачам, в которых более одного потока могут одновременно входить в систему или выходить из нее. Особо следует отметить тот факт, что задачи последовательной и параллельной системы трубопроводов решаются с помощью уравнения Бернулли.
Пример: уравнение Бернулли
Предположим, что поток без трения в длинной горизонтальной конической трубе. Диаметр составляет 2,0 фута на одном конце и 4,0 фута на другом. Напор на меньшем конце составляет 16 футов водяного столба.Если вода течет через этот конус со скоростью 125,6 фут3 / сек, найдите скорости на двух концах и напор на большем конце.
Решение:
V˙ 1 = A 1 v 1
v 1 = V˙ 1 / A 1 v 2 = 2 / A 2
v 1 = 125.6 футов 3 / сек / π (1 фут) 2 v 2 = 125,6 футов 3 / сек / π (2 фута) 2
v 1 = 40 футов / с v 2 = 10 футов / с
z 1 + v 1 2 / 2g + P 1 ν 1 g c / g = z 2 + v 2 2 / 2g + P 2 ν 2 g c / g
P 2 ν 2 g c / g = P 1 ν 1 g c / g + (z 1 — z 2 ) + (v 1 2 — v 2 2 ) / 2g
= 16 футов + 0 футов + [(40 футов / сек) 2 — (10 футов / сек) 2 /2 (32.17 фут-фунт-сила / фунт-сила — сек 2 )]
= 39,3 фута
Ограничения упрощенного уравнения Бернулли
Практическое применение упрощенного уравнения Бернулли к реальным трубопроводным системам невозможно из-за двух ограничений. Одно серьезное ограничение уравнения Бернулли в его нынешней форме состоит в том, что при решении проблем трубопроводов недопустимо жидкое трение. Следовательно, уравнение 3-10 применимо только к идеальным жидкостям. Однако в действительности общий напор жидкости не может быть полностью перенесен из одной точки в другую из-за трения.Учет этих потерь напора даст гораздо более точное описание того, что происходит физически. Это особенно верно, потому что одна из задач насоса в гидравлической системе — преодоление потерь давления из-за трения трубы.
Второе ограничение в уравнении Бернулли состоит в том, что нельзя выполнять какую-либо работу с жидкостью или с ней. Это ограничение предотвращает анализ двух точек в потоке жидкости, если между двумя точками существует насос. Поскольку большинство проточных систем включает насосы, это существенное ограничение.К счастью, упрощенное уравнение Бернулли можно модифицировать таким образом, чтобы удовлетворительно учитывать потери напора и работу насоса.
Расширенный Бернулли
Уравнение Бернулли можно модифицировать, чтобы учесть прирост и потерю напора. Полученное уравнение, называемое расширенным уравнением Бернулли, очень полезно при решении большинства задач потока жидкости. Фактически, расширенное уравнение Бернулли, вероятно, используется больше, чем любое другое уравнение потока жидкости. Уравнение 3-12 является одной из форм расширенного уравнения Бернулли.
z
1 + v 1 2 / 2g + P 1 ν 1 g c / g + H p = z 2 + v 2 2 / 2g + P 2 ν 2 g c / g + H f (3-12)
где:
z = высота над исходным уровнем (футы)
v = средняя скорость жидкости ( фут / сек)
P = давление жидкости (фунт-сила / фут 2 )
ν = удельный объем жидкости (фут 3 / фунт-метр)
л.с. = напор, добавляемый насосом (футы)
Hf = потеря напора из-за гидравлического трения (футы)
g = ускорение свободного падения (фут / сек 2 )
Потеря напора из-за гидравлического трения (Hf) представляет собой энергию, используемую для преодоления трения, вызванного стенками трубка.Хотя это представляет собой потерю энергии с точки зрения потока текучей среды, обычно это не означает значительную потерю общей энергии текучей среды. Это также не нарушает закон сохранения энергии, поскольку потеря напора из-за трения приводит к эквивалентному увеличению внутренней энергии (u) жидкости. Эти потери являются наибольшими, когда жидкость протекает через входы, выходы, насосы, клапаны, фитинги и любые другие трубопроводы с шероховатой внутренней поверхностью.
Большинство методов оценки потери напора из-за трения являются эмпирическими (основанными почти исключительно на экспериментальных данных) и основаны на константе пропорциональности, называемой коэффициентом трения (f), который будет обсуждаться в следующем разделе.
Пример: Extended Bernoulli
Вода перекачивается из большого резервуара в точку на 65 футов выше резервуара. Сколько футов напора должно быть добавлено насосом, если через 6-дюймовую трубу течет 8000 фунтов / час, а потеря напора на трение составляет 2 фута? Плотность жидкости составляет 62,4 фунта / фут3, а площадь поперечного сечения 6-дюймовой трубы составляет 0,2006 футов 2 .
Решение:
Чтобы использовать модифицированную форму уравнения Бернулли, ориентиры выбираются на поверхности резервуара (точка 1) и на выходе из трубы (точка 2).Давление на поверхности резервуара такое же, как давление на выходе из трубы, то есть атмосферное давление. Скорость в точке 1 будет практически равна нулю.
Использование уравнения массового расхода для определения скорости в точке 2:
м˙ 2 = ρ A 2 v 2
v 2 = m˙ 2 / ρ A 2
v 2 = 8000 фунт / час / (62,4 фунт / фут 3 ) 0,2006 фут 2
v 2 = 639 фут / час (1 час / 3600 с)
v 2 = 0.178 фут / с
z 1 + v 1 2 / 2g + P 1 ν 1 g c / g + H p = z 2 + v 2 2 / 2g + P 2 ν 2 g c / g + H f
H p = (z 2 — z 1 ) + (v 2 2 — v 1 2 ) / 2g + (P 2 — P 1 ) ν (g c / g) + H f
H p = 65 футов + [(0.178 фут / сек) 2 — (o фут / сек) 2 ] / [2 (32,17 фут-фунт / фунт-сила-сек 2 )] + 0 футов + 2 фута
H p = 67 футов [/ box]
Следует отметить, что решение этой примерной задачи имеет числовое значение, которое «имеет смысл» из данных, приведенных в задаче. Общее увеличение напора на 67 футов в основном связано с увеличением оценки на 65 футов и увеличением напора трения на 2 фута.
Применение уравнения Бернулли к трубке Вентури
Многие компоненты установки, такие как трубка Вентури, могут быть проанализированы с использованием уравнения Бернулли и уравнения неразрывности.Вентури — это устройство для измерения расхода, которое состоит из постепенного сжатия с последующим постепенным расширением. Пример трубки Вентури показан на рисунке 6. Измеряя перепад давления между входом трубки Вентури (точка 1) и горловиной трубки Вентури (точка 2), можно определить скорость потока и массовый расход на основе формулы Бернулли. уравнение.
Рис. 6. Измеритель Вентури
Уравнение Бернулли утверждает, что общий напор потока должен быть постоянным. Так как высота не изменяется значительно, если вообще не изменяется между точками 1 и 2, высота напора в этих двух точках будет по существу одинакова и будет исключена из уравнения.Таким образом, уравнение Бернулли упрощается до уравнения 3-13 для трубки Вентури.
v
1 2 / 2g + P 1 ν 1 g c / g = v 2 2 / 2g + P 2 ν 2 g c / g (3-13)
Применение уравнения неразрывности к точкам 1 и 2 позволяет нам выразить скорость потока в точке 1 как функцию скорости потока в точке 2 и отношения двух областей потока.
ρ 1 A 1 v 1 = ρ 2 A 2 v 2
v 1 = ρ 2 A 2 v 2 / ρ A 1
v 1 = v 2 A 2 / A 1
Использование алгебры для преобразования уравнения 3-13 и замена вышеприведенного результата на v 1 позволяет нам решить для Версия 2 .
v 2 2 — v 1 2 / 2g = (P 1 –P 2 ) ν g c / g
v 2 2 — (v 2 A 2 / A 1 ) 2 = (P 1 — P 2 ) 2 ν g c
v 2 2 (1 — (A 2 / A 1 ) 2 ) = (P 1 — P 2 ) 2 ν g c
v 2 2 = (P 1 — P 2 ) 2 ν g c / (1 — (A2 / A1) 2 )
v 2 = √ [(P 1 — P 2 ) 2 ν g c / (1 — (A2 / A1) 2 )]
v 2 = √ (P 1 — P 2 ) √ [2 ν g c / (1 — (A2 / A1) 2 )]
Следовательно, скорость потока в горловине трубки Вентури и объемный расход являются прямыми y пропорционально квадратному корню из перепада давления.
Давления на участке выше по потоку и в горловине являются фактическими давлениями, а скорости из уравнения Бернулли без потерь являются теоретическими скоростями. Когда потери учитываются в уравнении энергии, скорости являются фактическими скоростями. Во-первых, с помощью уравнения Бернулли (то есть без члена потери напора) получается теоретическая скорость в горловине. Затем умножив это на коэффициент Вентури (C v ), который учитывает потери на трение и равен 0.98 для большинства Вентури получается фактическая скорость. Фактическая скорость, умноженная на фактическую площадь горловины, определяет фактический объемный расход нагнетания.
Падение давления P 1 — P 2 на трубке Вентури можно использовать для измерения расхода с помощью U-образного манометра, как показано на рисунке 6. Показание R ‘манометра пропорционально падению давления и, следовательно, скорости жидкости.
Основные положения этой главы кратко изложены ниже.
• Краткое изложение уравнения Бернулли
• Уравнение Бернулли представляет собой приложение Первого закона термодинамики.
• Уравнение Бернулли — это приложение общего уравнения энергии к системе с установившимся потоком, в которой никакая работа не совершается с жидкостью или текучей средой, тепло не передается к текучей среде или от нее, и не происходит никаких изменений внутренней энергии жидкости.
• Напор — это термин, используемый для описания давления, оказываемого на жидкость или со стороны жидкости.
• Поскольку жидкость течет в системе трубопроводов, изменения высоты, скорости и напора должны быть согласованными, чтобы удовлетворялось уравнение Бернулли.
• Уравнение Бернулли можно модифицировать, чтобы учесть потери на трение и работу насоса.
• Вентури можно использовать для определения массового расхода из-за изменений давления и скорости жидкости.
• Объемный расход через трубку Вентури прямо пропорционален квадратному корню из перепада давления между входом трубки Вентури и ее горловиной.
Потеря напора
Потеря напора — это мера уменьшения общего напора (сумма подъемного напора, скоростного напора и напора) жидкости при ее движении через жидкостную систему. В реальных жидкостях потеря напора неизбежна. Это происходит из-за: трения между жидкостью и стенками трубы; трение между соседними частицами жидкости при их движении относительно друг друга; и турбулентность, вызываемая всякий раз, когда поток перенаправляется или каким-либо образом влияет на такие компоненты, как входы и выходы трубопроводов, насосы, клапаны, редукторы потока и фитинги.
Потери на трение — это часть общей потери напора, которая возникает, когда жидкость течет по прямым трубам. Потеря напора для потока жидкости прямо пропорциональна длине трубы, квадрату скорости жидкости и члену, учитывающему трение жидкости, называемому коэффициентом трения. Потеря напора обратно пропорциональна диаметру трубы.
Потеря напора ∝ f Lv 2 / D
Коэффициент трения
Было установлено, что коэффициент трения зависит от числа Рейнольдса для потока и степени шероховатости внутренней поверхности трубы.
Величина, используемая для измерения шероховатости трубы, называется относительной шероховатостью, которая равна средней высоте неровностей поверхности (ε), деленной на диаметр трубы (D).
Относительная шероховатость = ε / D
Значение коэффициента трения обычно получают из диаграммы Moody Chart (Рисунок A). Диаграмму Moody Chart можно использовать для определения коэффициента трения на основе числа Рейнольдса и относительной шероховатости.
Рисунок A: Диаграмма Moody Пример:
Определите коэффициент трения (f) для потока жидкости в трубе с числом Рейнольдса 40 000 и относительной шероховатостью 0.01.
Solution:
Используя диаграмму Moody Chart, число Рейнольдса 40 000 пересекает кривую, соответствующую относительной шероховатости 0,01 при коэффициенте трения 0,04.
Уравнение Дарси
Потери напора на трение могут быть рассчитаны с использованием математической зависимости, известной как уравнение Дарси для потери напора. Уравнение принимает две различные формы. Первая форма уравнения Дарси определяет потери в системе, связанные с длиной трубы.
H
r = f L v 2 / D 2 g (3-14)
где:
f = коэффициент трения (без агрегата)
L = длина трубы (футы)
D = диаметр трубы (футы)
v = скорость жидкости (фут / сек)
g = ускорение свободного падения (фут / сек 2 )
Пример:
Уравнение потери напора Дарси Труба длиной 100 футов и диаметром 20 дюймов содержит воду при температуре 200 ° F, протекающую с массовым расходом 700 фунтов / м3.Вода имеет плотность 60 фунтов / фут 3 и вязкость 1,978 x 10 -7 фунт-сила-сек / фут 2 . Относительная шероховатость трубы 0,00008. Рассчитайте потерю напора для трубы.
Решение:
Для решения этой проблемы необходимо сначала определить скорость потока. Во-вторых, используя скорость потока и заданные свойства жидкости, вычислите число Рейнольдса. В-третьих, определите коэффициент трения по числу Рейнольдса и относительной шероховатости.Наконец, используйте уравнение Дарси, чтобы определить потерю напора.
м˙ = ρ A v
v = м˙ / ρ A
= (700 фунт / сек) / (60 фунт / фут 3 ) π (10 дюймов) 2 (1 фут 2 / 144 дюйма 2)
v = 5,35 фут / сек
N R = ρ v D / мкг c
N R = (60 фунт / фут 3 ) (5,35 фут / сек) (20 дюймов) (1 фут / 12 дюймов) / (1,978 x 10 -7 фунт-сила-сек / фут 2 ) (32,17 фут-фунт-сила / фунт-сила-фут-сек 2) =
N R = 8.4 x 10 7
Используйте диаграмму Moody для числа Рейнольдса 8,4 x 10 7 и относительной шероховатости 0,00008.
f = 0,012
H f = f (L / D) (v 2 / 2g)
H f = (o.o12) [100 футов / (20 дюймов) (1 фут / 12 дюймов) )] * (5,35 фут / сек) 2 /(2)(32,17 фут / сек 2 )
H f = 0,32 фута
Незначительные потери
Потери, возникающие в трубопроводах из-за изгибов, локти, суставы, клапаны и т. д.иногда называют незначительными потерями. Это неправильное название, потому что во многих случаях эти потери более важны, чем потери из-за трения трубы, рассмотренные в предыдущем разделе. Для всех незначительных потерь в турбулентном потоке потеря напора изменяется пропорционально квадрату скорости. Таким образом, удобный метод выражения незначительных потерь потока — это коэффициент потерь (k). Значения коэффициента потерь (k) для типовых ситуаций и арматуры можно найти в стандартных справочниках. Форма уравнения Дарси, используемого для расчета незначительных потерь отдельных компонентов жидкостной системы, выражается уравнением 3-15.
H
f = kv 2 / 2g (3-15)
Эквивалентная длина трубопровода
Незначительные потери могут быть выражены через эквивалентную длину (Leq) трубы, которая будет иметь такую же потерю напора для такая же скорость нагнетаемого потока. Эту взаимосвязь можно найти, установив две формы уравнения Дарси равными друг другу.
f L v 2 / D 2g = kv 2 / 2g
Это дает два полезных соотношения
L
eq = k D / f (3-16)
k = f L
eq / D (3-17)
Типичные значения L eq / D для общих компонентов трубопроводной системы перечислены в таблице 1.Эквивалентная длина трубопровода, которая вызовет такую же потерю напора, как и конкретный компонент, может быть определена путем умножения значения L экв. / D для этого компонента на диаметр трубы. Чем выше значение L eq / D, тем длиннее эквивалентная длина трубы.
Таблица 1: Типичные значения Leq / D Пример:
Полностью открытая задвижка находится в трубе диаметром 10 дюймов. Какая эквивалентная длина трубы вызовет такую же потерю напора, как и задвижка?
Решение:
Из таблицы 1 мы находим, что значение L экв. / D для полностью открытой задвижки равно 10.
L eq = (L / D) D
= 10 (10 дюймов)
= 100 дюймов
Добавляя эквивалентные длины всех компонентов к фактической длине трубы в системе, мы можем получить L экв. значение для всей системы трубопроводов.
Основные положения этой главы кратко изложены ниже.
• Потеря напора — это уменьшение общего напора (сумма потенциального напора, скоростного напора и напора) жидкости, вызванное трением, присутствующим при движении жидкости.
• Потери на трение — это часть общей потери напора, которая возникает, когда жидкость течет по прямым трубам.
• Незначительные потери — это потери напора, возникающие из-за изгибов, колен, соединений, клапанов и других компонентов. Каждый раз, когда поток изменяет направление или изменяется площадь поперечного сечения, он испытывает потерю напора.
• Коэффициент трения для потока жидкости можно определить с помощью диаграммы Moody Chart, если можно определить относительную шероховатость трубы и число Рейнольдса потока.
• Уравнение Дарси можно использовать для расчета потерь на трение.
• Для расчета незначительных потерь можно использовать специальную форму уравнения Дарси.
• Длину трубы, которая вызовет такую же потерю напора, как у клапана или фитинга, можно определить, умножив значение L / D для компонента, указанного в справочниках или руководствах поставщиков, на диаметр трубы.
Принудительная и естественная циркуляция
В предыдущих главах, посвященных потоку жидкости, было объяснено, что каждый раз, когда жидкость течет, возникает некоторое трение, связанное с движением, которое вызывает потерю напора.Было указано, что эта потеря напора обычно компенсируется в трубопроводных системах насосами, которые действительно работают с жидкостью, компенсируя потерю напора из-за трения. Циркуляция жидкости в системах с помощью насосов обозначается как принудительная циркуляция .
Некоторые жидкостные системы можно спроектировать таким образом, чтобы не было необходимости в насосах для обеспечения циркуляции. Напор, необходимый для компенсации потерь напора, создается градиентами плотности и перепадами высоты.Поток, возникающий в этих условиях, называется естественной циркуляцией .
Тепловая приводная головка
Тепловая приводная головка — это сила, которая вызывает естественную циркуляцию. Это вызвано разницей в плотности между двумя телами или областями жидкости.
Рассмотрим два равных объема жидкости одного и того же типа. Если два объема имеют разную температуру, тогда объем с более высокой температурой также будет иметь меньшую плотность и, следовательно, меньшую массу.Поскольку объем при более высокой температуре будет иметь меньшую массу, на него также будет оказываться меньшая сила тяжести. Эта разница в силе тяжести, действующей на жидкость, будет приводить к тому, что более горячая жидкость поднимается, а более холодная жидкость опускается.
Этот эффект наблюдается во многих местах. Один из примеров — воздушный шар. Сила, заставляющая воздушный шар подниматься вверх, является результатом разницы в плотности между горячим воздухом внутри воздушного шара и более холодным воздухом, окружающим его.
Тепло, добавляемое к воздуху в воздушном шаре, добавляет энергию молекулам воздуха. Движение молекул воздуха увеличивается, и молекулы воздуха занимают больше места. Молекулы воздуха внутри воздушного шара занимают больше места, чем такое же количество молекул воздуха вне воздушного шара. Это означает, что горячий воздух менее плотный и легкий, чем окружающий воздух. Поскольку воздух в воздушном шаре менее плотный, сила тяжести оказывает на него меньшее влияние. В результате воздушный шар весит меньше окружающего воздуха.Гравитация втягивает более холодный воздух в пространство, занимаемое воздушным шаром. Движение более холодного воздуха вниз выталкивает воздушный шар из ранее занятого пространства, и он поднимается.
Условия, необходимые для естественной циркуляции
Естественная циркуляция будет иметь место только при наличии правильных условий. Даже после того, как естественное кровообращение началось, устранение любого из этих условий приведет к остановке естественного кровообращения. Условия естественной циркуляции следующие.
1. Существует разница температур (имеется источник тепла и радиатор).
2. Источник тепла находится ниже радиатора.
3. Жидкости должны контактировать друг с другом.
Должны быть два тела жидкости с разными температурами. Это также может быть одно жидкое тело с участками с разной температурой. Разница в температуре необходима для разницы в плотности жидкости. Разница в плотности является движущей силой естественного циркуляционного потока.
Для продолжения естественной циркуляции необходимо поддерживать разницу температур. Добавление тепла от источника тепла должно происходить в зоне с высокой температурой. В области низких температур должен существовать непрерывный отвод тепла радиатором. В противном случае температуры в конечном итоге выровнялись бы, и дальнейшая циркуляция прекратилась.
Источник тепла должен располагаться ниже радиатора. Как показано на примере воздушного шара, более теплая жидкость менее плотна и будет иметь тенденцию подниматься, а более холодная жидкость более плотная и будет иметь тенденцию опускаться.Чтобы воспользоваться преимуществом естественного движения теплых и холодных жидкостей, источник тепла и радиатор должны располагаться на соответствующей высоте.
Две области должны соприкасаться, чтобы был возможен поток между ними. Если путь потока заблокирован или заблокирован, естественная циркуляция невозможна.
Пример охлаждения с естественной циркуляцией
Естественная циркуляция часто является основным средством охлаждения реакторов бассейнового типа и облученных тепловыделяющих сборок, хранящихся в бассейнах с водой после извлечения из реактора.Источником тепла является тепловыделяющая сборка. Радиатор — это основная часть воды в бассейне.
Вода в нижней части тепловыделяющей сборки поглощает энергию, генерируемую сборкой. Температура воды повышается, а плотность уменьшается. Сила тяжести втягивает более холодную (более плотную) воду в нижнюю часть узла, вытесняя более теплую воду. Более теплая (более легкая) вода вынуждена уступить свое место более холодной (более тяжелой) воде. Более теплая (более легкая) вода поднимается выше в сборке. По мере продвижения воды по длине сборки она поглощает больше энергии.Вода становится все светлее и светлее, непрерывно выталкиваясь вверх более плотной водой, движущейся под ней. В свою очередь, более холодная вода поглощает энергию от узла и также вынуждена подниматься по мере продолжения естественного циркуляционного потока. Вода, выходящая из верхней части топливной сборки, отдает свою энергию, смешиваясь с большей частью воды в бассейне. Основная часть воды в бассейне обычно охлаждается путем циркуляции через теплообменники в отдельном процессе.
Расход и разница температур
Тепловая приводная головка, которая вызывает естественную циркуляцию, возникает из-за изменения плотности, вызванного разницей температур.Как правило, чем больше разница температур между горячей и холодной областями жидкости, тем больше тепловая приводная головка и результирующая скорость потока. Однако рекомендуется держать горячую жидкость переохлажденной, чтобы предотвратить изменение фазы. Можно иметь естественную циркуляцию в двухфазном потоке, но, как правило, поддерживать поток труднее.
Для индикации или проверки естественной циркуляции могут использоваться различные параметры. Это зависит от типа растения.Например, для реактора с водой под давлением (PWR) выбранные параметры системы охлаждения реактора (RCS), которые будут использоваться, следующие.
1. RCS ∆T (T Hot — T Cold ) должен составлять 25-80% от значения полной мощности и должен быть постоянным или медленно уменьшаться. Это указывает на то, что остаточное тепло удаляется из системы с достаточной скоростью для поддержания или снижения внутренней температуры.
2. RCS Температура горячих и холодных ног должна быть постоянной или медленно снижаться. Опять же, это указывает на то, что тепло удаляется, а тепловая нагрузка распада уменьшается, как и ожидалось.
3. Давление пара парогенератора (давление вторичного контура) должно соответствовать температуре RCS. Это подтверждает, что парогенератор отводит тепло от охлаждающей жидкости RCS.
Если естественная циркуляция для PWR происходит или неизбежна, можно выполнить несколько действий, чтобы обеспечить или улучшить возможности охлаждения активной зоны. Во-первых, уровень в компенсаторе давления может поддерживаться выше 50%. Во-вторых, поддерживайте переохлаждение RCS на уровне 15 o F или выше.
Оба эти действия помогут предотвратить образование паровых карманов в RCS, где они ограничили бы поток RCS.В-третьих, поддерживайте уровень воды в парогенераторе ≥ нормального диапазона. Это обеспечивает соответствующий теплоотвод, чтобы гарантировать, что отвод тепла будет достаточным для предотвращения закипания RCS.
Основные положения этой главы перечислены ниже.
• Естественный циркуляционный поток — это циркуляция жидкости без использования механических устройств.
• Принудительный циркуляционный поток — это циркуляция жидкости в системе с помощью насосов.
• Тепловая приводная головка является движущей силой для естественной циркуляции, вызванной разницей в плотности между двумя областями жидкости.
• Для поддержания естественной циркуляции необходимы три элемента:
- Должны быть теплоотвод и источник тепла.
- Источник тепла должен располагаться под радиатором.
- Между теплой и холодной жидкостью должны существовать пути потока.
• Как правило, чем больше разница температур, тем выше расход естественной циркуляции.
• Естественная циркуляция в PWR может быть проверена путем мониторинга:
- RCS ∆T — 25% -80% значение полной мощности
- T Hot / T Cold — устойчиво или медленно снижение
- Давление пара S / G — отслеживание температуры RCS
• Естественная циркуляция в PWR может быть увеличена за счет:
- поддерживать уровень компенсатора давления> 50%
- поддерживать RCS ≥ 15o F переохлаждение
- поддерживать адекватный теплоотвод, уровень S / G ≥ нормальный диапазон
Двухфазный поток жидкости
Все отношения потоков жидкости, обсужденные ранее, относятся к потоку одной фазы жидкости, будь то жидкость или пар .В некоторых важных местах в системах потока жидкости происходит одновременный поток жидкой воды и пара, известный как двухфазный поток. Этих простых соотношений, используемых для анализа однофазного потока, недостаточно для анализа двухфазного потока.
Существует несколько методов, используемых для прогнозирования потери напора из-за трения жидкости для двухфазного потока. Трение двухфазного потока больше, чем трение однофазного потока, при тех же размерах трубопровода и массовом расходе. Разница, по-видимому, зависит от типа потока и является результатом увеличения скорости потока.Потери на двухфазное трение экспериментально определяются путем измерения перепада давления на различных элементах трубопровода.
Двухфазные потери обычно связаны с однофазными потерями через те же элементы. Один принятый метод определения потерь на двухфазное трение на основе однофазных потерь включает множитель двухфазного трения (R), который определяется как отношение двухфазных потерь напора к потерям напора, оцененным с использованием насыщенного жидкие свойства.
R = H
f, двухфазный / H f, насыщенная жидкость (3-18)
где:
R = двухфазный множитель трения (без единиц)
H f, два -фаза = двухфазная потеря напора из-за трения (футы)
H f, насыщенная жидкость = однофазная потеря напора из-за трения (футы)
Множитель трения (R) оказался намного выше при более низких давлениях, чем при более высоких давлениях.Двухфазная потеря напора может быть во много раз больше, чем однофазная потеря напора.
Хотя для моделей двухфазного потока использовался широкий диапазон названий, мы определим только три типа потока. Используемые схемы потока определены следующим образом:
1. Пузырьковый поток: происходит рассеяние пузырьков пара в непрерывном потоке жидкости.
2. Пробковый поток: в пузырьковом потоке пузырьки растут за счет слияния и в конечном итоге становятся того же диаметра, что и труба. При этом образуются типичные пузыри пулевидной формы, характерные для снарядного режима.
3. Кольцевой поток: теперь жидкость распределяется между жидкой пленкой, текущей вверх по стенке, и дисперсией капель, текущих в паровом ядре потока.
Нестабильность потока
Неустойчивый поток может возникать в виде колебаний потока или его реверсирования. Колебания потока — это изменения потока из-за образования пустот или механических препятствий при проектировании и производстве. Колебания потока в одном канале теплоносителя реактора иногда вызывают колебания потока в окружающих каналах теплоносителя из-за перераспределения потока.Колебания потока нежелательны по нескольким причинам. Во-первых, устойчивые колебания потока могут вызывать нежелательную вынужденную механическую вибрацию компонентов. Это может привести к выходу этих компонентов из строя из-за усталости. Во-вторых, колебания потока могут вызвать проблемы управления системой, имеющие особое значение в ядерных реакторах с жидкостным охлаждением, поскольку теплоноситель также используется в качестве замедлителя. В-третьих, колебания потока влияют на местные характеристики теплообмена и кипение. В ходе испытаний было обнаружено, что критический тепловой поток (CHF), необходимый для отклонения от пузырькового кипения (DNB), может быть снижен на целых 40%, когда поток колеблется.Это сильно снижает тепловой предел и плотность мощности по длине активной зоны реактора. Опять же, в ходе испытаний было обнаружено, что колебания потока не являются серьезной проблемой для некоторых реакторов с водой под давлением, если мощность не превышает 150% для нормальных условий потока. Колебания потока могут быть проблемой при работе с естественной циркуляцией из-за присутствующих низких скоростей потока.
Во время естественной циркуляции пузырьки пара, образующиеся при колебаниях потока, могут иметь достаточно влияния, чтобы фактически вызвать полное реверсирование потока в затронутом канале.
И колебания потока, и реверсирование потока приводят к очень нестабильному состоянию, поскольку паровые покровы, образующиеся на нагретых поверхностях, напрямую влияют на способность отводить тепло от этих поверхностей.
Штыревой патрубок
В случае разрыва трубы сила реакции, создаваемая высокоскоростной струей жидкости, может вызвать смещение трубопровода и серьезное повреждение компонентов, контрольно-измерительных приборов и оборудования в зоне разрыва. Эта характеристика аналогична необслуживаемому садовому шлангу или пожарному шлангу, который непредсказуемо «хлестает».Этот тип отказа анализируется, чтобы свести к минимуму повреждение, если бы труба изгибалась в непосредственной близости от оборудования, связанного с безопасностью.
Гидравлический удар
Гидравлический удар — это ударная волна жидкости, возникающая в результате внезапного начала или остановки потока. На него влияют начальное давление в системе, плотность жидкости, скорость звука в жидкости, эластичность жидкости и трубы, изменение скорости жидкости, диаметр и толщина трубы, а также клапан. рабочее время.
Во время закрытия клапана кинетическая энергия движущейся жидкости преобразуется в потенциальную энергию. Эластичность жидкости и стенки трубы создает волну положительного давления, направленную обратно к источнику жидкости. Когда эта волна достигнет источника, масса жидкости будет в покое, но под огромным давлением. Сжатая жидкость и растянутые стенки трубы теперь начнут выпускать жидкость из трубы обратно к источнику и вернуться к статическому давлению источника. Это высвобождение энергии сформирует еще одну волну давления, возвращающуюся к клапану.Когда эта ударная волна достигает клапана, из-за импульса жидкости стенка трубы начинает сокращаться. Это сжатие передается обратно источнику, что снижает давление в трубопроводе ниже статического давления источника. Эти волны давления будут перемещаться вперед и назад несколько раз, пока трение жидкости не демпфирует переменные волны давления до статического давления источника. Обычно весь процесс молота занимает менее одной секунды.
Первоначальный толчок внезапной остановки потока может вызвать переходные изменения давления, превышающие статическое давление.Если клапан закрывается медленно, потеря кинетической энергии будет постепенной. Если его закрыть быстро, потеря кинетической энергии будет очень быстрой. Из-за быстрой потери кинетической энергии возникает ударная волна. Ударная волна, вызванная гидравлическим ударом, может иметь достаточную силу, чтобы вызвать физическое повреждение трубопроводов, оборудования и персонала. Гидравлический удар в трубах, как известно, срывает опоры труб с их креплений, разрывает трубопроводы и вызывает биение труб.
Пик давления
Пик давления — это результирующий быстрый рост давления выше статического, вызванный гидроударами.Максимальный всплеск давления будет в момент изменения расхода и регулируется следующим уравнением.
∆P = ρ c ∆v / g c
где:
∆P = скачок давления (фунт-сила / фут 2 )
ρ = плотность жидкости (фунт / фут 3 )
c = Скорость волны давления (фут / сек) (Скорость звука в жидкости)
∆v = Изменение скорости жидкости (фут / сек)
gc = Гравитационная постоянная 32.17 (фунт-фут / фунт-сила-сек 2 )
Пример:
Скачок давления Вода с плотностью 62,4 фунт / фут 3 и давлением 120 фунтов на квадратный дюйм течет по трубе со скоростью 10 футов / сек. Скорость звука в воде 4780 футов / сек. Внезапно закрылся обратный клапан. Какое максимальное давление жидкости в фунтах на квадратный дюйм?
Раствор
P Макс = P статический + ΔP Пик
P Макс = 120 фунт-сила / дюйм 2 + ρ c ΔV / g c
P 920 = 120 фунт-сила / дюйм 2 + (62.4 фунта / фут 3 ) (4780 фут / с) (10 фут / с) / (32,17 фунт-фут / фунт-сила с 2 )
P Макс. = 120 фунт-сила / дюйм 2 + 64,3 фунта-силы / дюйм 2
P Макс = 76,3 фунта / кв. дюйм
Паровой молот
Паровой молот похож на гидравлический удар, за исключением того, что он предназначен для паровой системы. Паровой молот — это газовая ударная волна, возникающая в результате внезапного запуска или остановки потока. Паровой молот не так силен, как гидравлический, по трем причинам:
1.Сжимаемость пара гасит ударную волну.
2. Скорость звука в паре составляет примерно одну треть скорости звука в воде.
3. Плотность пара примерно в 1600 раз меньше плотности воды.
Проблемы, связанные с паропроводом, включают термический удар и водяные пробки (то есть конденсацию в паровой системе) в результате неправильного нагрева.
Рекомендации по эксплуатации
Гидравлический и паровой молот — не редкость на промышленных предприятиях.Изменения расхода в трубопроводных системах должны производиться медленно, что является частью надлежащей практики оператора. Чтобы предотвратить гидравлический и паровой удар, операторы должны обеспечить надлежащую вентиляцию жидкостных систем и обеспечить надлежащий слив газовых или паровых систем во время запуска. Если возможно, инициируйте запуск насоса при закрытом нагнетательном клапане и медленно откройте нагнетательный клапан, чтобы запустить поток в системе. Если возможно, запускайте насосы меньшей производительности перед насосами большей производительности. По возможности используйте клапаны разогрева вокруг запорных клапанов основного потока.Если возможно, закройте нагнетательные клапаны насоса перед остановкой насосов. Периодически проверяйте правильность работы влагоуловителей и воздухоотводчиков во время работы.
Основные положения этой главы кратко изложены ниже.
Комбинация жидкости и пара, протекающей по трубе, называется двухфазным потоком.
Типы двухфазного потока включают:
• Пузырьковый поток: происходит рассеяние пузырьков пара в непрерывном потоке жидкости.
• Пробковый поток: пузырьки растут за счет слияния и в конечном итоге становятся того же диаметра, что и труба, образуя пузырьки в форме пули.
• Кольцевой поток: жидкость распределяется между жидкой пленкой, текущей вверх по стенке, и дисперсией капель, текущей в паровом ядре потока.
Колебания и нестабильность потока керна могут вызвать:
• нежелательную механическую вибрацию компонентов.
• уменьшение теплового потока, необходимого для возникновения DNB.
• прерывание фактического циркуляционного потока.
Колебания и нестабильность потока могут возникать в следующих условиях:
• сердечник находится вне проектных условий, мощность> 150%
• механический отказ, вызывающий закупорку потока
• недостаточное охлаждение активной зоны во время естественная циркуляция, при которой происходит кипение.
Изгиб трубы — это смещение трубопровода, создаваемое реакционными силами высокоскоростной струи жидкости после разрыва трубы.
Гидравлический удар — это ударная волна жидкости, возникающая в результате внезапного начала или остановки потока.
Преобразование энергии в центробежном насосе
Жидкость, поступающая в центробежный насос, сразу же направляется в зону низкого давления в центре или в проушине рабочего колеса. При вращении крыльчатки и лопастей они передают импульс поступающей жидкости. Передача количества движения движущейся жидкости увеличивает скорость жидкости. По мере увеличения скорости жидкости увеличивается ее кинетическая энергия.Жидкость с высокой кинетической энергией вытесняется из области рабочего колеса и попадает в улитку.
Улитка — это область с постоянно увеличивающейся площадью поперечного сечения, предназначенная для преобразования кинетической энергии жидкости в давление жидкости. Механизм этого преобразования энергии такой же, как и для дозвукового потока через расширяющуюся часть сопла. Математический анализ потока через улитку основан на общем уравнении энергии, уравнении неразрывности и уравнении, связывающем внутренние свойства системы.Ключевыми параметрами, влияющими на преобразование энергии, являются увеличивающаяся площадь поперечного сечения улитки, более высокое противодавление системы на выходе улитки и несжимаемый дозвуковой поток жидкости. В результате взаимозависимости этих параметров поток жидкости в улитке, аналогичный дозвуковому потоку в расширяющемся сопле, испытывает уменьшение скорости и увеличение давления.
Рабочие характеристики центробежного насоса
Рис. 7: Типичные характеристики центробежного насоса Кривая
Обычно центробежный насос создает относительно небольшое повышение давления в жидкости.Это повышение давления может составлять от нескольких десятков до нескольких сотен фунтов на квадратный дюйм в центробежном насосе с одноступенчатым рабочим колесом. Термин PSID (фунт-сила на квадратный дюйм дифференциала) эквивалентен ∆P. В данном контексте это разница давлений на всасывании и нагнетании насоса. PSID также можно использовать для описания перепада давления в компоненте системы (сетчатые фильтры, фильтры, теплообменники, клапаны, деминерализаторы и т. Д.). Когда центробежный насос работает с постоянной скоростью, увеличение противодавления системы на текущий поток вызывает уменьшение величины объемной скорости потока, которую центробежный насос может поддерживать.
Анализ взаимосвязи между объемным расходом (), который центробежный насос V˙ может поддерживать, и перепадом давления в насосе (∆Ppump) основан на различных физических характеристиках насоса и жидкости в системе. Переменные, оцениваемые инженерами-конструкторами для определения этой взаимосвязи, включают эффективность насоса, мощность, подаваемую на насос, скорость вращения, диаметр рабочего колеса и лопастей, плотность жидкости и вязкость жидкости. Результат этого сложного анализа для типичного центробежного насоса, работающего на одной конкретной скорости, показан на графике на рисунке 7.
Напор насоса по вертикальной оси — это разница между противодавлением в системе и давлением на входе насоса (∆Ppump). Объемный расход (V) по горизонтальной оси — это скорость, с которой жидкость протекает через насос. График предполагает одну конкретную скорость (N) для рабочего колеса насоса.
Кавитация
Когда перекачиваемая жидкость попадает в проушину центробежного насоса, давление значительно снижается. Чем больше скорость потока через насос, тем больше падение давления.Если перепад давления достаточно велик или если температура жидкости достаточно высока, перепад давления может быть достаточным, чтобы заставить жидкость мгновенно превращаться в пар, когда местное давление падает ниже давления насыщения для перекачиваемой жидкости. Эти пузырьки пара перемещаются вдоль рабочего колеса насоса вместе с жидкостью. По мере уменьшения скорости потока давление жидкости увеличивается. Это вызывает внезапное схлопывание пузырьков пара на внешних частях крыльчатки. Образование этих пузырьков пара и их последующее схлопывание — кавитация.
Кавитация может быть очень серьезной проблемой для центробежных насосов. Некоторые насосы могут быть рассчитаны на работу с ограниченным количеством кавитации. Большинство центробежных насосов не могут выдерживать кавитацию в течение значительных периодов времени; они повреждаются из-за эрозии рабочего колеса, вибрации или других проблем, вызванных кавитацией.
Чистый положительный напор на всасывании
Чтобы избежать кавитации во время работы насоса, можно контролировать чистый положительный напор на всасывании насоса.Чистый положительный напор на всасывании (NPSH) для насоса — это разница между давлением всасывания и давлением насыщения перекачиваемой жидкости. NPSH используется для измерения того, насколько жидкость близка к насыщенным условиям. Уравнение 3-19 можно использовать для расчета чистой положительной высоты всасывания, доступной для насоса. Единицы NPSH — футы воды.
NPSH = P
всасывание — P насыщение (3-19)
где:
P всасывание = давление всасывания насоса
P насыщение = давление насыщения для жидкости
При поддержании доступный NPSH на уровне больше, чем NPSH, требуемый производителем насоса, кавитации можно избежать.
Законы о насосах
Центробежные насосы обычно подчиняются так называемым законам о насосах. Эти законы гласят, что скорость потока или производительность прямо пропорциональны скорости насоса; напор прямо пропорционален квадрату скорости насоса; и мощность, требуемая двигателем насоса, прямо пропорциональна кубу скорости насоса. Эти законы суммированы в следующих уравнениях.
V˙ ∝ n (3-20)
H
P ∝ n 2 (3-21)
P ∝ n
3 (3-22)
где:
n = скорость рабочее колесо насоса (об / мин)
V = объемный расход насоса (галлонов в минуту или фут3 / час)
H p = напор, развиваемый насосом (фунты на квадратный дюйм или футы)
p = мощность насоса (кВт)
Используя эти пропорциональности, можно разработать уравнения, связывающие условия на одной скорости с условиями на другой скорости.
V˙
1 (n 2 / n 1 ) = V 2 (3-23)
H
p1 (n 2 / n 1 ) 2 = H p2 (3-24)
P
1 (n 2 / n 1 ) 3 = P 2 (3-25)
Пример: законы насоса
Насос охлаждающей воды работает на скорости 1800 об / мин. Его расход составляет 400 галлонов в минуту при напоре 48 футов. Мощность насоса составляет 45 кВт.Определите расход, напор и мощность насоса, если скорость насоса увеличится до 3600 об / мин.
Решение:
Расход
V˙ 2 = V˙ 1 (n 2 / n 1 )
= (400 галлонов в минуту) (3600 об / 1800 об / мин)
= 800 галлонов в минуту
Напор
H p2 = H p1 (n 2 / n 1 ) 2
= 48 футов (3600 об / 1800 об / мин) 2
= 192 футов
Мощность
P 2 = P 1 (n 2 / n 1 ) 3
= 45 кВт (3600 об / 1800 об / мин) 3
= 360 кВт
Рисунок 8 : Изменение скоростей центробежного насоса
Можно построить характеристическую кривую для новой скорости насоса на основе кривой для его исходной скорости.Метод состоит в том, чтобы взять несколько точек на исходной кривой и применить законы насоса для определения нового напора и расхода при новой скорости. Кривая зависимости напора насоса от расхода, которая возникает в результате изменения скорости насоса, графически проиллюстрирована на Рисунке 8.
Характеристическая кривая системы
Рисунок 9: Типичная кривая потери напора в системе
В главе, посвященной потере напора, было определено, что оба фрикционные потери и незначительные потери в трубопроводных системах были пропорциональны квадрату скорости потока.Поскольку скорость потока прямо пропорциональна объемному расходу, потеря давления в системе должна быть прямо пропорциональна квадрату объемного расхода. Исходя из этого соотношения, можно построить кривую потери напора в системе в зависимости от объемного расхода. Кривая потери напора для типичной системы трубопроводов имеет форму параболы, как показано на рисунке 9.
Рабочая точка системы
Рисунок 10: Рабочая точка для центробежного насоса
Точка, в которой насос работает в данной системе трубопроводов, зависит от от расхода и потери напора этой системы.Для данной системы объемный расход сравнивается с потерями напора в системе на характеристической кривой. Построив график характеристической кривой системы и характеристической кривой насоса в одной и той же системе координат, можно определить точку, в которой насос должен работать. Например, на рисунке 10 рабочая точка центробежного насоса в исходной системе обозначена пересечением кривой насоса и кривой системы (h Lo ).
Система имеет расход, равный V˙ 0 , и полную потерю напора в системе, равную ∆P 0 .Для поддержания расхода V˙ 0 напор насоса должен быть равен ∆P o . В системе, описанной системной кривой (h L1 ), в системе был открыт клапан, чтобы уменьшить сопротивление системы потоку. Для этой системы насос поддерживает большой расход (V˙ 1 ) при меньшем напоре насоса (∆P 1 ).
Использование в системе нескольких центробежных насосов
Типичный центробежный насос имеет относительно небольшое количество движущихся частей и может быть легко адаптирован к различным первичным двигателям.Эти первичные двигатели включают электродвигатели переменного и постоянного тока, дизельные двигатели, паровые турбины и пневмодвигатели. Центробежные насосы, как правило, имеют небольшие размеры и могут быть изготовлены с относительно низкими затратами. Кроме того, центробежные насосы обеспечивают высокий объемный расход при относительно низком давлении.
Для увеличения объемного расхода в системе или для компенсации больших сопротивлений потоку центробежные насосы часто используются параллельно или последовательно. На рисунке 11 изображены два идентичных центробежных насоса, работающих параллельно с одинаковой скоростью.
Рисунок 11: Кривая характеристик насоса для двух идентичных центробежных насосов, используемых параллельно
Центробежные насосы, подключенные параллельно
Поскольку вход и выход каждого насоса, показанные на рисунке 11, находятся в идентичных точках в системе, каждый насос должен производить один и тот же насос глава. Однако общий расход в системе представляет собой сумму индивидуальных расходов для каждого насоса.
Когда характеристическая кривая системы рассматривается с кривой для параллельных насосов, рабочая точка на пересечении двух кривых представляет более высокий объемный расход, чем для одиночного насоса, и большую потерю напора в системе.Как показано на Рисунке 12, большая потеря напора в системе происходит с увеличением скорости жидкости в результате увеличения объемного расхода. Из-за большего напора системы объемный расход фактически в два раза меньше расхода, достигаемого при использовании одного насоса.
Рис. 12: Рабочая точка для двух параллельных центробежных насосов
Центробежные насосы серии
Центробежные насосы используются последовательно для преодоления больших потерь напора в системе, чем один насос может компенсировать по отдельности.Как показано на Рисунке 13, два идентичных центробежных насоса, работающих с одинаковой скоростью и одинаковым объемным расходом, создают одинаковый напор. Поскольку вход второго насоса является выходом первого насоса, напор, создаваемый обоими насосами, является суммой отдельных напоров. Объемный расход от входа первого насоса до выхода второго остается прежним.
Рисунок 13: Кривая характеристик насоса для двух идентичных центробежных насосов, используемых в серии
Как показано на Рисунке 14, использование двух насосов последовательно не увеличивает сопротивление потоку в системе вдвое.Два насоса обеспечивают достаточный напор для новой системы, а также поддерживают немного более высокий объемный расход.
Рис. 14: Рабочая точка для двух центробежных насосов серии
Ниже приведены основные моменты этой главы.
• Чистый положительный напор на всасывании — это разница между давлением всасывания насоса и давлением насыщения жидкости.
• Кавитация — это образование и последующее схлопывание пузырьков пара на рабочем колесе насоса, когда местное давление падает ниже, а затем поднимается выше давления насыщения перекачиваемой жидкости.
• Законы насоса можно использовать для определения влияния изменения скорости центробежного насоса на расход, напор и мощность.
V˙ 1 (n 2 / n 1 ) = V˙ 2
H p1 (n 2 / n 1 ) 2 = H p2
P 1 (n 2 / n 1 ) 3 = P 2
• Кривая комбинированного насоса для двух центробежных насосов, подключенных параллельно, может быть определена путем сложения индивидуальные потоки для любой данной головы.
• Комбинированная характеристика насоса для двух последовательно включенных центробежных насосов может быть определена путем добавления отдельных напоров для любого заданного расхода.
• Рабочая точка (напор и расход) системы может быть определена путем построения кривой насоса и кривой потери напора системы на одних и тех же осях. Система будет работать на пересечении двух кривых.
.

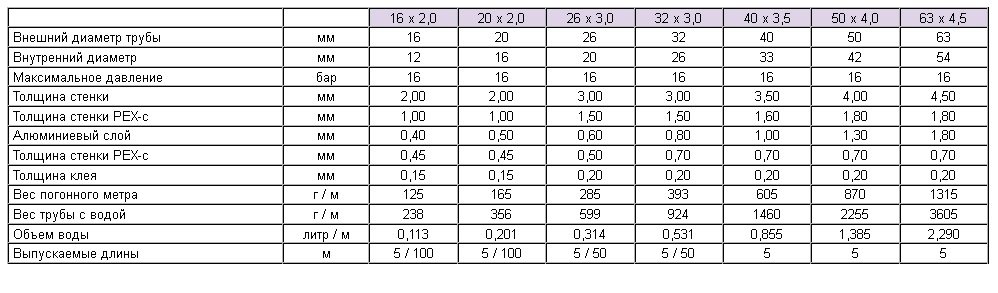 .. подробнее
.. подробнее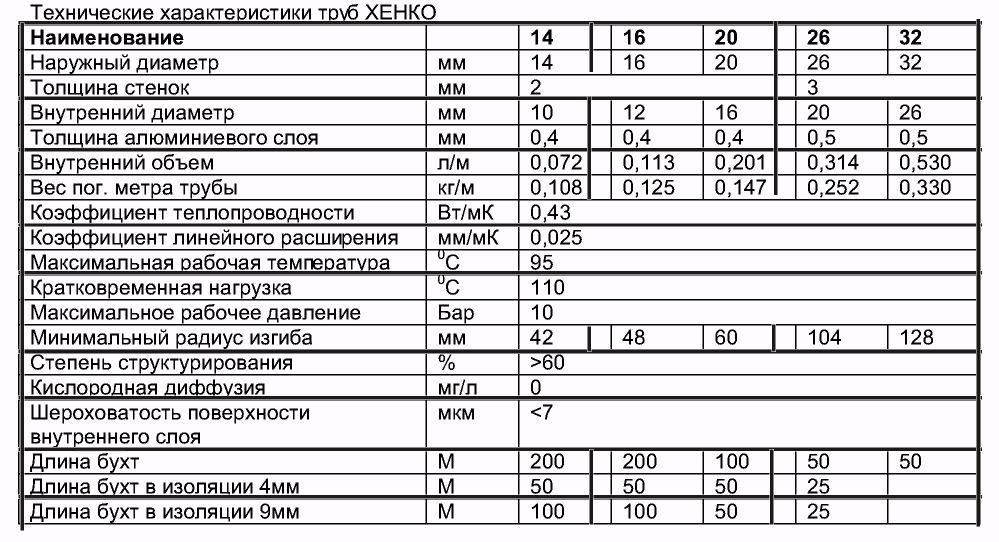 Привод насосов данных …… подробнее
Привод насосов данных …… подробнее