Ecoplast CUG50 Угол 90 градусов (единый) для труб D50мм 41150-5 Муфта поворота
Ecoplast CUG50 Угол 90 градусов (единый) для труб D50мм 41150-5 Муфта поворота
Вход
Если у Вас есть зарегистрированный акаунт,
пожалуйста авторизуйтесь
Восстановление пароля
Ссылка на страницу изменения пароля будет отправлена на адрес Вашей электронной
почты.
Вернуться на форму авторизации
ГлавнаяМуфтыПоворотEcoplast CUG50 Угол 90 градусов (единый) для труб D50мм 41150-5
{{:description}}
{{:price}}
{{:name}}
Достоинства
{{:advantages}}
Недостатки
{{:disadvantages}}
Комментарий
{{:comment_divided}}
{{:product_score_stars}}
{{:useful_score}}
{{:useless_score}}
CUG50 Угол 90 градусов (единый) для труб D50мм
Купить по низким ценам Ecoplast CUG50 Угол 90 градусов (единый) для труб D50мм 41150-5
Описание Ecoplast CUG50 Угол 90 градусов (единый) для труб D50мм 41150-5
Угол единый 90° типа ТРУБА-ТРУБА для гофрированной или жесткой гладкой трубы выполнен из АБС пластика.
Предназначен для соединения труб гофрированных или жестких под углом 90°.
Угол, как правило, используется для соединения жестких гладких труб, образуя обвод под 90° в жестком исполнении.
Технические характеристики:
- Ед. измерения: упак.
- Тип: Аксессуары для труб
- Тип аксессуара: Углы
- Диаметр: 50 мм
- Цвет: Серый, RAL 7035
- Класс защиты: IP40
Технические характеристики Ecoplast CUG50 Угол 90 градусов (единый) для труб D50мм 41150-5
- Ширина упаковки
10 см - Высота упаковки
10 см org/PropertyValue»> - Объемный вес
1 кг
Глубина упаковки
10 см
- Единица измерения
уп - Кратность поставки
1 - Тип
муфта соединительная
Заказ в один клик
Мы позвоним Вам в ближайшее время
Несоответствие минимальной сумме заказ
Минимальная сумма заказа 1 500,00 ₽
Просьба увеличить заказ.
Гарантия производителя 1 год
Миссией организации экопласт является обеспечить качественные современные и доступные материалы большому количеству клиентов. Повсеместное применение подобного материала происходит при установке внутренней и открытой электропроводки.
При вводе запроса в поисковую систему сайт экопласт, выдается больше 250 тысяч сылок на сайты с подобной информацией. Это свидетельствует о широком применении подобных материалов. Огромное количество специализированных магазинов предоставляют продукцию по электрооборудованию. Но сайт экопласт предоставляет более дешевые модели, не уступающие по качеству товару с прилавков магазинов. На это сказываются следующие моменты:
Срочная доставка день в день
Объемный вес: 1 кг
Габариты: 10x10x10
* только для города Москва
Самовывоз по РФ
Объемный вес: 1 кг
Габариты: 10x10x10
Выберите пункт самовывозаМосква, ул. веерная, дом 7 к.2, офис 2
Доставка курьером по РФ
Объемный вес: 1 кг
Габариты: 10x10x10
По России:
| Собственная служба доставки | 350 ₽ | 2-3 дней | |
| Почта России | уточнять | 3-20 дней | |
| ПЭК | уточнять | 2-7 дней | |
| СДЭК | Экспресс лайт | уточнять | 2-7 дней |
| СДЭК | Супер Экспресс | уточнять | 2-4 дней |
| Деловые Линии | уточнять | 2-7 дней | |
| Pony Express | уточнять | 2-7 дней | |
| DPD | уточнять | 2-7 дней | |
| DHL | уточнять | 2-7 дней | |
| Boxberry | уточнять | 2-7 дней | |
| ЖелДорЭкспедиция | уточнять | 3-10 дней | |
| Байкал Сервис | уточнять | 2-10 дней | |
| Энергия | уточнять | 2-7 дней | |
Ecoplast CUG50 Угол 90 градусов (единый) для труб D50мм 41150-5
Артикул: 41150-5
CUG50 Угол 90 градусов (единый) для труб D50мм
Объемный вес: 1 кг
Габариты:
10x10x10
Сравнить
В наличии
2 418,41 ₽
Скидка 20%
1 934,73 ₽
Цена за 1 уп
От 20 шт:
1 934,73 ₽
1 837,99 ₽
От 40 шт:
1 837,99 ₽
1 741,26 ₽
Задать вопрос
Мы позвоним Вам в ближайшее время
Номер телефона
Вопрос
Заказ на обратный звонок
Мы позвоним Вам в ближайшее время
Номер телефона
Вопрос
Обратный звонок
Мы позвоним Вам в ближайшее время
Номер телефона
Вопрос
Центральные и вписанные углы.
 Как найти?
Как найти?
Поможем понять и полюбить математику
Начать учиться
213.9K
Угол и окружность: на первый взгляд — ничего общего. Давайте разберемся, что же такого привлекательного в этих углах, что окружность все время позволяет им вписываться.
Центральный угол и вписанный угол
Окружность — замкнутая линия, все точки которой равноудалены от ее центра.
Определение центрального угла:
Центральный угол — это угол, вершина которого лежит в центре окружности.
Центральный угол равен градусной мере дуги, на которую он опирается.
На рисунке: центральный угол окружности EOF и дуга, на которую он опирается EF
Определение вписанного угла:
Вписанный угол — это угол, вершина которого лежит на окружности.
Вписанный угол равен половине дуги, на которую опирается.
На рисунке: вписанный в окружность угол ABC и дуга, на которую он опирается AC
Узнай, какие профессии будущего тебе подойдут
Пройди тест — и мы покажем, кем ты можешь стать, а ещё пришлём подробный гайд, как реализовать себя уже сейчас
Свойства центральных и вписанных углов
Углы просты только на первый взгляд. Свойства центрального угла и свойства вписанного угла помогут решать задачки легко и быстро.
- Вписанный угол в два раза меньше, чем центральный угол, если они опираются на одну и ту же дугу:
Угол AOC — центральный, угол ABC — вписанный. Оба угла опираются на дугу AC, в этом случае центральный угол равен дуге AC, а угол ABC равен половине угла AOC.
- Теорема о центральном угле: центральный угол равен градусной мере дуги, на которую он опирается:
ㄥAOB = ◡ AB
- Вписанные углы окружности равны друг другу, если опираются на одну дугу:
ㄥADC = ㄥABC = ㄥAEC, поскольку все три угла, вписанные в окружность, опираются на одну дугу AC.
- Вписанный в окружность угол, опирающийся на диаметр, — всегда прямой:
ㄥACB опирается на диаметр и на дугу AB, диаметр делит окружность на две равные части. Значит дуга AB = 180 ํ, ㄥCAB равен половине дуги, на которую он опирается, значит ㄥCAB = 90 ํ.
Если есть вписанный, обязательно найдется и описанный угол. Описанный угол — это угол, образованный двумя касательными к окружности. Вот так:
На рисунке: ㄥCAB, образованный двумя касательными к окружности. AO — биссектриса ㄥCAB, значит центр окружности лежит на биссектрисе описанного угла.
Для решения задачек мало знать, какой угол называется вписанным, а какой — описанным. Нужно знать, что такое хорда и ее свойство.
Нужно быстро привести знания в порядок перед экзаменом? Записывайтесь на курсы ЕГЭ по математике в Skysmart!
Хорда — отрезок, соединяющий две точки на окружности.
- Если две хорды в окружности пересекаются, то произведения отрезков одной равно произведению отрезков другой.
AB * AC = AE * AD
Получается, что стороны вписанного в окружность угла — это хорды.
- Если вписанные углы опираются на одну и ту же хорду — они равны, если их вершины находятся по одну сторону от хорды.
ㄥBAC = ㄥCAB, поскольку лежат на хорде BC.
- Если два вписанных угла опираются на одну и ту же хорду, то их суммарная градусная мера равна 180°, если их вершины находятся по разные стороны от хорды.
ㄥBAC + ㄥBDC = 180°
Примеры решения задач
Центральный, вписанные и описанные углы, как и любые другие, требуют тренировок в решении. Рассмотрите примеры решения задач и потренируйтесь самостоятельно.
Задачка 1. Дана окружность, дуга AC = 200°, дуга BC = 80°. Найдите, чему равен вписанный угол, опирающийся на дугу AB. ㄥACB = ?
Дана окружность, дуга AC = 200°, дуга BC = 80°. Найдите, чему равен вписанный угол, опирающийся на дугу AB. ㄥACB = ?
Как решаем: окружность 360° − AC − CB = 360° − 200° − 80° = 80°
По теореме: вписанный угол равен дуге ½.
ㄥACB = ½ AB = 40°
Задачка 2. Дана окружность, ㄥAOC = 140°, найдите, чему равна величина вписанного угла.
Мы уже потренировались и знаем, как найти вписанный угол.
На рисунке в окружности центральный угол и дуга AC = 140°
Мы знаем, что вписанный угол равен половине центрального, то ㄥABC = ½ AC = 140/2 = 70°
Задачка 3. Чему равен вписанный в окружность угол, опирающийся на дугу, если эта дуга = ⅕ окружности?
СB = ⅕ от 360° = 72°
Вписанный угол равен половине дуги, поэтому ㄥCAB = ½ от CB = 72° / 2 = 36°
Шпаргалки для родителей по математике
Все формулы по математике под рукой
Анастасия Белова
К предыдущей статье
209. 4K
4K
Факториал
К следующей статье
259.5K
Прямоугольный параллелепипед. Что это такое?
Получите план обучения, который поможет понять и полюбить математику
На вводном уроке с методистом
Выявим пробелы в знаниях и дадим советы по обучению
Расскажем, как проходят занятия
Подберём курс
Измерение углов
Измерение углов
Концепция угла
Понятие угла — одно из важнейших понятий геометрии. Понятия равенства, суммы и разности углов важны и используются во всей геометрии, но предмет тригонометрии основан на измерении углов.
Существуют две широко используемые единицы измерения углов. Более привычной единицей измерения являются градусы. Окружность разделена на 360 равных градусов, так что прямой угол равен 90°. Градусы могут быть далее разделены на минуты и секунды, но это деление уже не так универсально, как раньше. Каждый градус делится на 60 равных частей, называемых минутами. Итак, семь с половиной градусов можно назвать 7 градусов и 30 минут, записав 7° 30′. Каждая минута далее делится на 60 равных частей, называемых 9.0004 секунды, и, например, 2 градуса 5 минут 30 секунд записывается как 2° 5′ 30″. Деление градусов на минуты и угловые секунды аналогично делению часов на минуты и секунды времени. |
Части градуса теперь обычно указываются в десятичном виде. Например, семь с половиной градусов теперь обычно записывают как 7,5°.
Когда для анализа нарисован один угол на плоскости xy , мы нарисуем его за стандартная позиция с вершиной в начале координат (0,0), одна сторона угла вдоль оси x , а другая сторона над осью x .
радианы
Другой распространенной единицей измерения углов являются радианы. Для этого измерения рассмотрим единичную окружность (окружность радиуса 1), центр которой является вершиной рассматриваемого угла. Тогда угол отсекает дугу окружности, и длина этой дуги является мерой угла в радианах. Легко конвертировать между измерением в градусах и измерением в радианах. Длина окружности всего круга 2 π , отсюда следует, что 360° равняется 2 π радиан. Следовательно, и Большинство калькуляторов можно настроить на использование углов, измеряемых в градусах или радианах. Убедитесь, что вы знаете, какой режим использует ваш калькулятор. |
Краткая заметка об истории радианов
Хотя слово «радиан» было придумано Томасом Мьюиром и/или Джеймсом Томпсоном примерно в 1870 году, математики давно измеряли углы таким способом. Например, Леонард Эйлер (1707–1783) в своих « элементах алгебры » прямо сказал, что углы измеряются длиной дуги, отсеченной в единичной окружности. Это было необходимо, чтобы дать его знаменитую формулу с комплексными числами, которая связывает функции знака и косинуса с показательной функцией.
Например, Леонард Эйлер (1707–1783) в своих « элементах алгебры » прямо сказал, что углы измеряются длиной дуги, отсеченной в единичной окружности. Это было необходимо, чтобы дать его знаменитую формулу с комплексными числами, которая связывает функции знака и косинуса с показательной функцией.
e iθ = cos θ + i sin θ
где θ — это то, что позже было названо измерением угла в радианах. К сожалению, объяснение этой формулы выходит далеко за рамки этих заметок. Но для получения дополнительной информации о комплексных числах см. мой Краткий курс комплексных чисел.
Радианы и длина дуги
Альтернативное определение радианов иногда дается как отношение. Вместо того, чтобы взять единичную окружность с центром в вершине угла θ , возьмем любую окружность с центром в вершине угла. Тогда радианной мерой угла является отношение длины стягиваемой дуги к радиусу r окружности. Например, если длина дуги равна 3, а радиус окружности равен 2, то мера радиана равна 1,5.
Например, если длина дуги равна 3, а радиус окружности равен 2, то мера радиана равна 1,5.
Причина, по которой это определение работает, заключается в том, что длина стягиваемой дуги пропорциональна радиусу окружности. В частности, определение в терминах отношения дает ту же цифру, что и приведенная выше, с использованием единичного круга. Однако это альтернативное определение более полезно, поскольку его можно использовать для связи длин дуг с углами. Длина дуги равна радиусу r , умноженное на угол θ , где угол измеряется в радианах.
Например, дуга θ = 0,3 радиана в окружности радиусом r = 4 имеет длину 0,3 умножить на 4, то есть 1,2.
Радианы и площадь сектора
Сектором окружности называется та часть окружности, которая ограничена двумя радиусами и дугой окружности, соединяющей их концы. Площадь этого сектора легко вычислить по радиусу r окружности и угол θ между радиусами, если он измеряется в радианах. Так как площадь всего круга равна πr 2 , а сектор относится ко всему кругу как угол θ к 2 π , поэтому
Так как площадь всего круга равна πr 2 , а сектор относится ко всему кругу как угол θ к 2 π , поэтому
Углы общие
Ниже приведена таблица общих углов как в градусах, так и в радианах. Обратите внимание, что измерение в радианах дается как π . Его, конечно, можно было бы представить десятичным числом, но радианное измерение часто появляется с коэффициентом 9.0004 №
.
| Уголок | градусов | радиан |
|---|---|---|
| 90° | № /2 | |
| 60° | № /3 | |
| 45° | № /4 | |
| 30° | № /6 |
Упражнения
Эдвин С. Кроули написал книгу «Тысяча упражнений в плоской и сферической тригонометрии», Университет Пенсильвании, Филадельфия, 1914 г. Задачи этого краткого курса взяты из этого текста (но не все 1000 из них!) Он дал свои задачи с точностью до пяти знаков, поэтому учащимся пришлось поработать над их решением, и они использовали таблицы логарифмов, чтобы помочь в умножении и делении. Студенты должны были уметь пользоваться таблицей синусов-косинусов, тангенсов, логарифмов, логарифмических синусоидальных и логарифмических таблиц. Теперь мы можем использовать калькуляторы! Это означает, что вы можете сосредоточиться на концепциях, а не на трудоемких вычислениях.
Задачи этого краткого курса взяты из этого текста (но не все 1000 из них!) Он дал свои задачи с точностью до пяти знаков, поэтому учащимся пришлось поработать над их решением, и они использовали таблицы логарифмов, чтобы помочь в умножении и делении. Студенты должны были уметь пользоваться таблицей синусов-косинусов, тангенсов, логарифмов, логарифмических синусоидальных и логарифмических таблиц. Теперь мы можем использовать калькуляторы! Это означает, что вы можете сосредоточиться на концепциях, а не на трудоемких вычислениях.
Кроули использовал не десятичную запись для долей градуса, а минуты и секунды.
Каждый набор упражнений включает, во-первых, формулировки упражнений, во-вторых, несколько советов по решению упражнений и, в-третьих, ответы на упражнения.
1. Выразите следующие углы в радианах.
(а). 12 градусов 28 минут, то есть 12° 28′.
(б). 36° 12′.
2. Сократите следующие числа радианов до градусов, минут и секунд.
(а). 0,47623.
(б). 0,25412.
3. Учитывая угол a и радиус r, найти длину стягивающей дуги.
(а). a = 0° 17′ 48″, r = 6,2935.
(б). a = 121° 6′ 18″, r = 0,2163.
4. Зная длину дуги l и радиус r, найти угол, опирающийся на центр.
(а). l = 0,16296, r = 12,587.
(б). l = 1,3672, r = 1,2978.
5. Зная длину дуги l и угол a , на который она опирается в центре, найти радиус.
(а). a = 0° 44′ 30″, l = 0,032592.
(б). a = 60° 21′ 6″, l = 0,4572.
6. Найдите длину с точностью до дюйма дуги окружности 11 градусов 48,3 минуты, если радиус равен 3200 футов.
7. Железнодорожная кривая образует дугу окружности 9 градусов 36,7 минуты, радиус от центральной линии пути составляет 2100 футов. Если ширина колеи 5 футов, найдите разницу в длине двух рельсов с точностью до полдюйма.
Если ширина колеи 5 футов, найдите разницу в длине двух рельсов с точностью до полдюйма.
9. На сколько человек изменит широту, пройдя на север одну милю, если предположить, что Земля представляет собой сферу радиусом 3956 миль?
10. Вычислите длину одной угловой минуты в футах по большому кругу Земли. Какова длина одной угловой секунды?
14. На окружности радиусом 5,782 метра длина дуги 1,742 метра. На какой угол он сужается в центре?
23. Известно, что воздушный шар диаметром 50 футов вытягивается из глаза под углом 8 1/2 минут. Как далеко это?
Подсказки
1. Чтобы преобразовать градусы в радианы, сначала преобразуйте количество градусов, минут и секунд в десятичную форму. Разделите количество минут на 60 и прибавьте к количеству градусов. Так, например, 12 ° 28 ‘это 12 + 28/60, что равно 12,467°. Далее умножить на π и разделите на 180, чтобы получить угол в радианах.
2. И наоборот, чтобы преобразовать радианы в градусы, разделите π и умножьте на 180. Таким образом, 0,47623, деленное на π и умноженное на 180, дает 27,286°. Вы можете преобразовать доли градуса в минуты и секунды следующим образом. Умножьте дробь на 60, чтобы получить количество минут. Здесь 0,286 умножить на 60 равно 17,16, поэтому угол можно записать как 27° 17,16′. Затем возьмите любую оставшуюся долю минуты и снова умножьте на 60, чтобы получить количество секунд. Здесь 0,16 умножить на 60 примерно равно 10, поэтому угол можно также записать как 27° 17′ 10″.
3. Чтобы найти длину дуги, сначала переведите угол в радианы. Для 3(a) 0°17’48» составляет 0,0051778 радиан. Затем умножьте на радиус, чтобы найти длину дуги.
4. Чтобы найти угол, разделите его на радиус. Это дает вам угол в радианах. Это можно преобразовать в градусы, чтобы получить ответы Кроули.
5. Как упоминалось выше, радиан умножить на радиус = длине дуги, поэтому, используя буквы для этой задачи, ar = l, , но a необходимо сначала преобразовать из градусов в радианы. Итак, чтобы найти радиус r, сначала преобразуйте угол a в радианы, а затем разделите его на длину l дуги.
Итак, чтобы найти радиус r, сначала преобразуйте угол a в радианы, а затем разделите его на длину l дуги.
6. Длина дуги равна произведению радиуса на угол в радианах.
7. Помогает нарисовать фигуру. Радиус внешней направляющей равен 2102,5, а радиус внутренней направляющей равен 209.7.5.
9. У вас есть окружность радиусом 3956 миль и дуга этой окружности длиной 1 миля. Какой угол в градусах? (Средний радиус Земли был известен довольно точно в 1914 году. Посмотрите, сможете ли вы узнать, каким Эратосфен считал радиус Земли еще в третьем веке до нашей эры.)
10. Угловая минута равна 1/60 градуса. Преобразовать в радианы. Радиус равен 3956. Какова длина дуги?
14. Поскольку длина дуги равна радиусу, умноженному на угол в радианах, отсюда следует, что угол в радианах равен длине дуги, деленной на радиус. Радианы легко перевести в градусы.
23. Представьте, что диаметр воздушного шара является частью дуги окружности, в центре которой вы находитесь. (Это не совсем часть дуги, но довольно близко.) Эта дуга имеет длину 50 футов. Вы знаете угол, так каков радиус этого круга?
Представьте, что диаметр воздушного шара является частью дуги окружности, в центре которой вы находитесь. (Это не совсем часть дуги, но довольно близко.) Эта дуга имеет длину 50 футов. Вы знаете угол, так каков радиус этого круга?
Ответы
1. (а). 0,2176. (б). 0,6318.
2. (а). 27° 17′ 10 дюймов (б). 14,56 ° = 14 °33,6′ = 14°33’36».
3. (а). 0,03259 (б). 2,1137 умножить на 0,2163 равно 0,4572.
4. (а). 0,16296/12,587 = 0,012947 радиан = 0° 44′ 30″.
(б). 1,3672/1,2978 = 1,0535
радианы = 60,360° = 60° 21,6′ = 60° 21′ 35″.
5. (а). л/год = 0,032592/0,01294 = 2,518.
(б). л/год = 0,4572/1,0533 = 0,4340.
6. ra = (3200′) (0,20604) = 659,31′ = 659′ 4 дюйма.
7. Угол a = 0,16776 радиан. Разница в длинах есть
2102.5 a – 1997.5 a , что составляет 5 a. Таким образом, ответ равен 0,84 фута, что с точностью до дюйма равно 10 дюймам.
9. Угол = 1/3956 = 0,0002528 радиан = 0,01448° = 0,8690′ = 52,14″.
10. Одна минута = 0,0002909 радиан. 1,15075 мили = 6076 футов. Поэтому одна секунда будет соответствовать 101,3 фута.
14. a = л/об = 1,742/5,782 = 0,3013 радиан = 17,26° = 17°16′.
23. Угол a равен 8,5′, что составляет 0,00247 радиана. Значит радиус равен r = л/год = 50/0,00247 = 20222′ = 3,83 мили, почти четыре мили.
О разрядах точности.
Кроули старается давать свои ответы примерно с той же точностью, что и данные в вопросах. Это важно, особенно сейчас, когда у нас есть калькуляторы. Например, в задаче 1 исходная точка равна 12°28′, что имеет точность около четырех знаков, поэтому ответ 0,2176 также должен быть дан с точностью только до четырех знаков. (Обратите внимание, что начальные нули не учитываются при подсчете цифр точности.) Ответ 0,21758438 предполагает восемь цифр точности, и это может ввести в заблуждение, поскольку данная информация не была такой точной.
Другой пример см. в задаче 3(а). Данные равны 0°17’48» и 6,2935 с точностью до 4 и 5 цифр соответственно. Поэтому ответ должен быть дан только с точностью до 4 цифр, поскольку ответ не может быть более точным, чем наименее точные данные. Таким образом, ответ, который может дать калькулятор, а именно 0,032586547, следует округлить до четырех цифр (не считая ведущих нулей) до 0,03259.
Хотя окончательные ответы должны быть выражены с соответствующим количеством цифр точности, вы все равно должны сохранить все цифры для промежуточных вычислений.
Измерение и построение углов — макеты
Авторы: Марк Райан и
Обновлено: 21 декабря 2021 г.
Из книги: Геометрия для чайников 9 0012
Геометрия для чайников
Исследуйте книгу Купить на Amazon
На карте вы прокладываете свой маршрут и подходите к развилке дорог. Две расходящиеся дороги выходят из общей точки и образуют угол . Точка, в которой дороги расходятся, — это вершина . Угол отделяет область вокруг себя, известную в геометрии как 9.0004 плоскость , на две области. Точки внутри угла лежат во внутренней области угла, а точки вне угла лежат во внешней области угла.
Две расходящиеся дороги выходят из общей точки и образуют угол . Точка, в которой дороги расходятся, — это вершина . Угол отделяет область вокруг себя, известную в геометрии как 9.0004 плоскость , на две области. Точки внутри угла лежат во внутренней области угла, а точки вне угла лежат во внешней области угла.
Как только вы узнаете типы углов и способы их измерения и создания, вы приобретете ценные навыки геометрии, которые помогут вам решить даже самые сложные геометрические головоломки.
Для выполнения обеих задач вы используете транспортир, очень полезный инструмент, который всегда под рукой (см. рис. 1).
Рис. 1. Удобный транспортир
При выборе транспортира постарайтесь найти его из прозрачного пластика. Вычислить меру угла проще, потому что вы можете видеть линию угла через транспортир.
Породы англов
Существует несколько различных угловых пород или типов. Определить, какая у вас порода угла, можно по его мерке. Наиболее распространенная мера угла в градусов . Вот краткое введение в четыре типа углов:
Вот краткое введение в четыре типа углов:
- Прямоугольный. С таким ракурсом вы никогда не ошибетесь. Прямой угол — один из самых легко узнаваемых углов. Он имеет форму буквы L и образует прямой угол (см. рис. 2). Он имеет меру 90 градусов.
Рисунок 2: Прямой угол
- Угол прямой. Знаешь что? На самом деле это прямая линия. Большинство людей даже не думают об этом типе как об угле, но это так. Прямой угол состоит из противоположных лучей или отрезков, имеющих общий конец (см. рис. 3). Этот угол имеет меру 180 градусов.
Прямые и прямые углы довольно легко определить, просто взглянув на них, но никогда не делайте поспешных выводов о величине угла. Лучше всего быть осторожным. Если информация не написана на странице, ничего не предполагайте. Мера.
Рисунок 3: Прямой уголок
- Острый угол. Это очаровательный угол .
- На самом деле, это всего лишь щепотка. Это любой угол, который больше 0 градусов, но меньше 90 градусов.
 Острый угол находится где-то между несуществующим и прямым углом (см. рис. 4).
Острый угол находится где-то между несуществующим и прямым углом (см. рис. 4).Рисунок 4: Острые углы при 45° (рис. a), 60° (рис. b) и 30° (рис. c)
- Тупой угол. Этот тип просто не так захватывающий, как острый угол. Его мера находится где-то между прямым углом и прямым углом (см. рисунок 5). Это холм, на который вы должны подняться, гора, на которую вы должны взойти. Он имеет меру больше 90 градусов, но меньше 180 градусов.
Рис. 5. Тупые углы при 95° (рис. a), 125° (рис. b) и 175° (рис. c)
Измерение углов
Углы чаще всего измеряются в градусах, но для тех из вас, кто является приверженцем точности, можно использовать даже более мелкие единицы измерения: минуты и секунды. Такие минуты и секунды подобны часам — минута больше секунды. Так что думайте о градусе как о часе, и вы поняли: один градус равен 60 минутам. Одна минута равна 60 секундам.
Прежде чем измерять угол, определите его и оцените, к какому типу, по вашему мнению, он относится.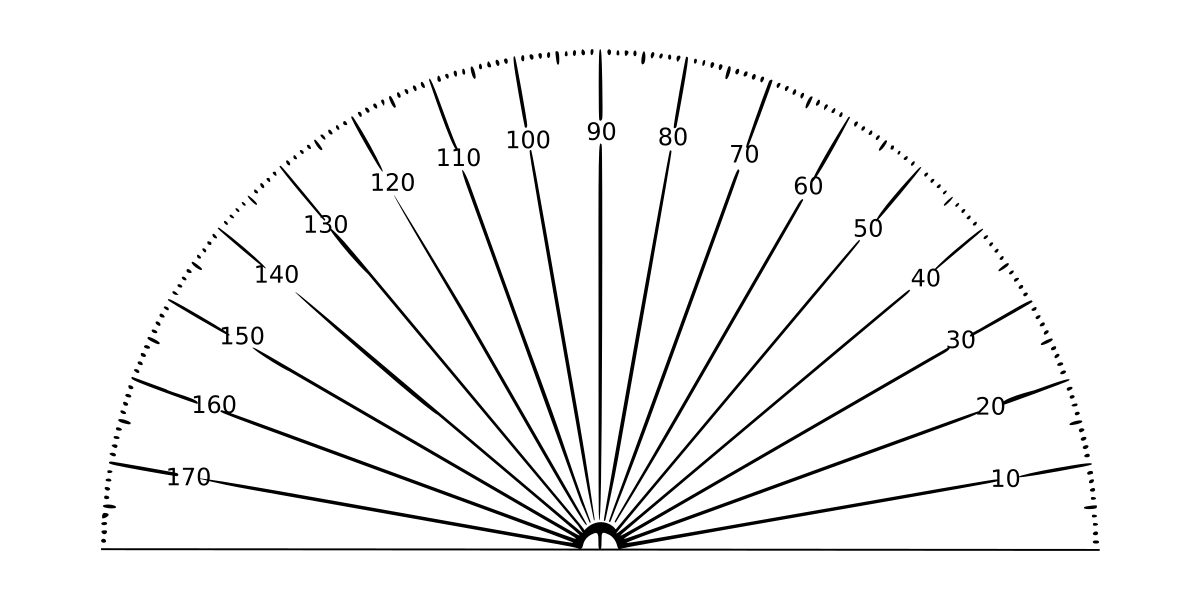 Это прямой угол? Прямой угол? Острый или тупой? После того, как вы его оцените, измерьте угол. Следуй этим шагам:
Это прямой угол? Прямой угол? Острый или тупой? После того, как вы его оцените, измерьте угол. Следуй этим шагам:
- Поместите выемку или центральную точку транспортира в точку, где сходятся стороны угла (вершина).
- Поместите транспортир так, чтобы одна из линий угла, который вы хотите измерить, была равна нулю (на самом деле это 0°).
Использование нулевой линии не обязательно, потому что вы можете измерить угол, получив разницу в градусах одной линии по отношению к другой. Однако проще измерить угол, когда одна его сторона находится на нулевой линии. Наличие одной линии на нулевой линии позволяет вам считывать измерения непосредственно с транспортира без необходимости выполнять дополнительные математические операции. (Но если вы готовы принять вызов, нокаутируйте себя.) - Считайте число с транспортира там, где вторая сторона угла встречается с транспортиром.
Еще несколько советов:
- Убедитесь, что ваша мера близка к вашей оценке.
 Это говорит вам, правильно ли вы выбрали шкалу. Если вы ожидали измерения острого угла, но получили серьезно тупой угол, вам нужно переосмыслить используемую вами шкалу. Попробуйте другой.
Это говорит вам, правильно ли вы выбрали шкалу. Если вы ожидали измерения острого угла, но получили серьезно тупой угол, вам нужно переосмыслить используемую вами шкалу. Попробуйте другой. - Если стороны вашего угла не достигают шкалы транспортира, удлините их так, чтобы они соответствовали. Это повысит точность измерения.
- Помните, что мера угла всегда является положительным числом.
Так что же делать, если ваш угол не совсем соответствует масштабу транспортира? Посмотрите на рисунок 6 для примера. Угол на этом рисунке имеет меру больше 180°. Что теперь? Извините, но в этом случае вам придется потратить немного больше энергии. Да, вам нужно заняться математикой. Эти углы известны как углы рефлекса, и их величина превышает 180°.
Рис. 6. Углы отражения не укладываются в шкалу транспортира, поэтому для их измерения необходимо произвести некоторые математические расчеты.
Нарисуйте линию так, чтобы получилась прямая линия (см. вытянутые точки на рис. 6). Эта часть угла равна 180°, потому что это прямой угол. Теперь измерьте угол, образованный выносной линией, которую вы только что сделали, и второй стороной исходного угла, который вы хотите измерить. (Если вы запутались, просто посмотрите на рисунок 6.) Как только вы получили меру второго угла, прибавьте это число к 180. Результатом будет общее количество градусов угла. На рисунке 6 180° + 45° = 225°.
6). Эта часть угла равна 180°, потому что это прямой угол. Теперь измерьте угол, образованный выносной линией, которую вы только что сделали, и второй стороной исходного угла, который вы хотите измерить. (Если вы запутались, просто посмотрите на рисунок 6.) Как только вы получили меру второго угла, прибавьте это число к 180. Результатом будет общее количество градусов угла. На рисунке 6 180° + 45° = 225°.
Об этой статье
Эта статья взята из книги:
- Геометрия для чайников,
Об авторе книги:
Марк Райан — основатель и владелец Математического центра в районе Чикаго, где он занимается репетиторством. по всем математическим предметам, а также при подготовке к экзаменам. Марк является автором книг «Исчисление для чайников», рабочей тетради по математическому анализу для чайников и рабочей тетради по геометрии для чайников .

 Пока мы будем рассматривать только углы от 0° до 360°, но позже, в разделе о тригонометрических функциях, мы будем рассматривать углы больше 360° и отрицательные углы.
Пока мы будем рассматривать только углы от 0° до 360°, но позже, в разделе о тригонометрических функциях, мы будем рассматривать углы больше 360° и отрицательные углы. Это говорит вам, правильно ли вы выбрали шкалу. Если вы ожидали измерения острого угла, но получили серьезно тупой угол, вам нужно переосмыслить используемую вами шкалу. Попробуйте другой.
Это говорит вам, правильно ли вы выбрали шкалу. Если вы ожидали измерения острого угла, но получили серьезно тупой угол, вам нужно переосмыслить используемую вами шкалу. Попробуйте другой.