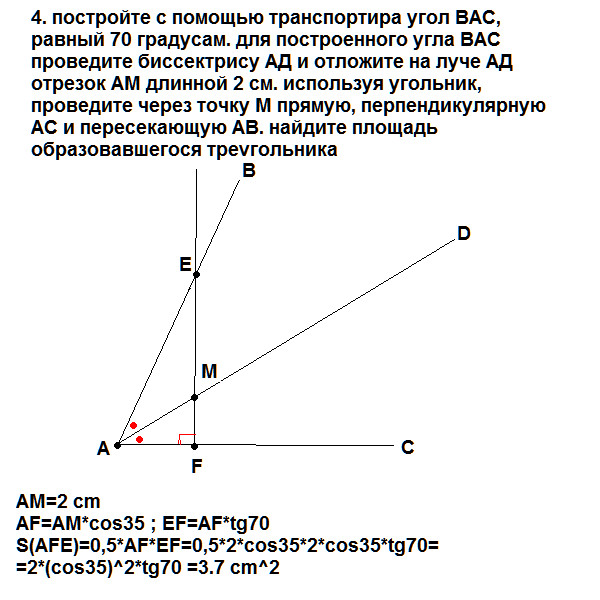
Синус(sin), косинус(cos), тангенс(tg), котангенс(ctg) — как найти, отношение, формулы
Изучение тригонометрии мы начнем с прямоугольного треугольника. Определим, что такое синус и косинус, а также тангенс и котангенс острого угла. Это основы тригонометрии.
Напомним, что прямой угол — это угол, равный 90 градусов. Другими словами, половина развернутого угла.
Острый угол — меньший 90 градусов.
Тупой угол — больший 90 градусов. Применительно к такому углу «тупой» — не оскорбление, а математический термин 🙂
Нарисуем прямоугольный треугольник. Прямой угол обычно обозначается C. Обратим внимание, что сторона, лежащая напротив угла, обозначается той же буквой, только маленькой. Так, сторона, лежащая напротив угла A, обозначается .
Угол A обозначается соответствующей греческой буквой .
Гипотенуза прямоугольного треугольника — это сторона, лежащая напротив прямого угла.
Катеты — стороны, лежащие напротив острых углов.
Катет , лежащий напротив угла , называется противолежащим (по отношению к углу ). Другой катет , который лежит на одной из сторон угла , называется прилежащим.
Синус острого угла в прямоугольном треугольнике — это отношение противолежащего катета к гипотенузе:
sin A
Косинус острого угла в прямоугольном треугольнике — отношение прилежащего катета к гипотенузе:
cos A
Тангенс острого угла в прямоугольном треугольнике — отношение противолежащего катета к прилежащему:
tg A
Другое (равносильное) определение: тангенсом острого угла называется отношение синуса угла к его косинусу:
tg A
Котангенс острого угла в прямоугольном треугольнике — отношение прилежащего катета к противолежащему (или, что то же самое, отношение косинуса к синусу):
ctg A
Обратите внимание на основные формулы для синуса, косинуса, тангенса и котангенса, которые приведены ниже.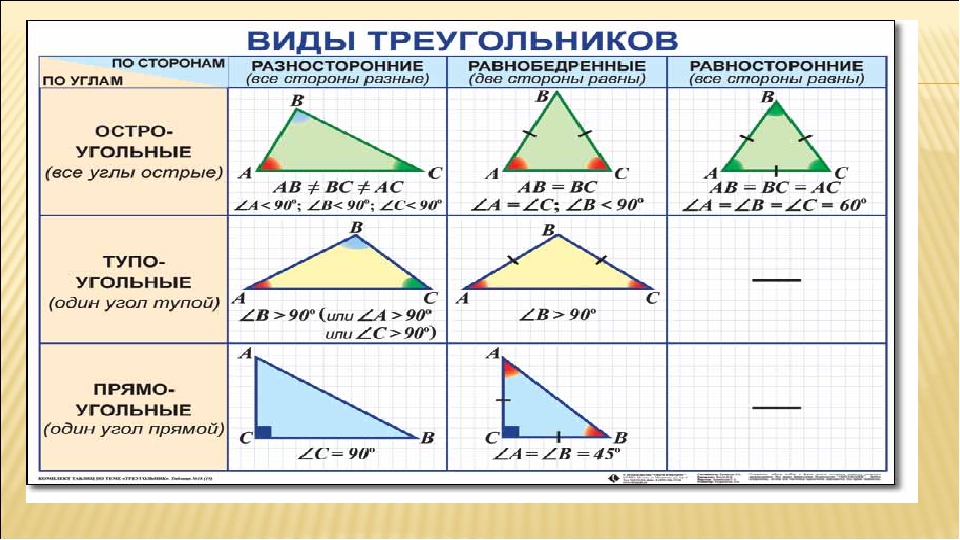 Они пригодятся нам при решении задач.
Они пригодятся нам при решении задач.
| sin | sincos | |
| cos | 1+tg | cos = sin |
| tg | 1+ctg | sin = cos |
| ctg | tg = ctg |
Давайте докажем некоторые из них.
- Сумма углов любого треугольника равна . Значит, сумма двух острых углов прямоугольного треугольника равнa .
- С одной стороны, как отношение противолежащего катета к гипотенузе. С другой стороны, , поскольку для угла катет а будет прилежащим. Получаем, что . Иными словами, .
- Возьмем теорему Пифагора: . Поделим обе части на получаем то есть
Мы получили основное тригонометрическое тождество. - Поделив обе части основного тригонометрического тождества на , получим: Это значит, что если нам дан тангенс острого угла , то мы сразу можем найти его косинус.
 Аналогично,
Аналогично,
Хорошо, мы дали определения и записали формулы. А для чего все-таки нужны синус, косинус, тангенс и котангенс?
Мы знаем, что сумма углов любого треугольника равна .
Знаем соотношение между сторонами прямоугольного треугольника. Это теорема Пифагора: .
Получается, что зная два угла в треугольнике, можно найти третий. Зная две стороны в прямоугольном треугольнике, можно найти третью. Значит, для углов — свое соотношение, для сторон — свое. А что делать, если в прямоугольном треугольнике известен один угол (кроме прямого) и одна сторона, а найти надо другие стороны?
С этим и столкнулись люди в прошлом, составляя карты местности и звездного неба. Ведь не всегда можно непосредственно измерить все стороны треугольника.
Синус, косинус и тангенс — их еще называют тригонометрическими функциями угла — дают соотношения между сторонами и углами треугольника. Зная угол, можно найти все его тригонометрические функции по специальным таблицам.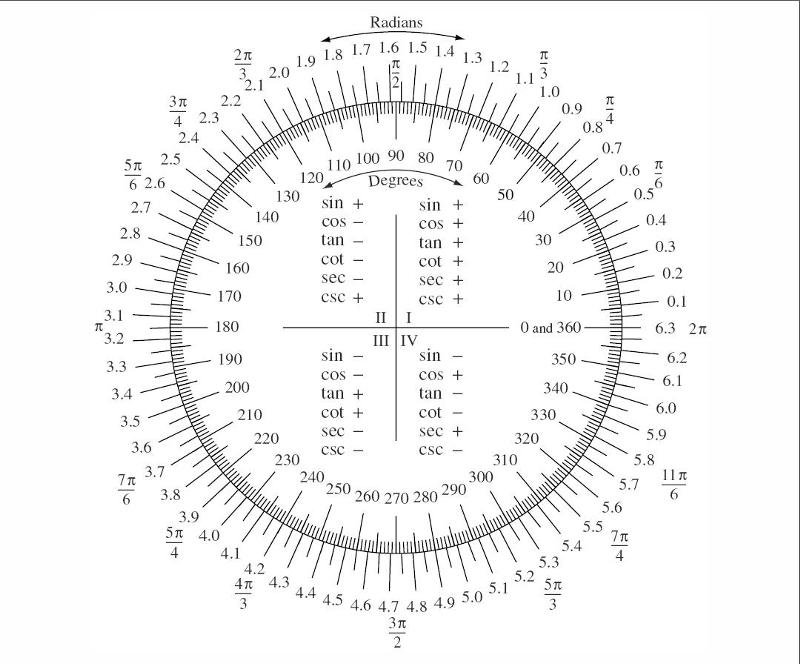 А зная синусы, косинусы и тангенсы углов треугольника и одну из его сторон, можно найти остальные.
А зная синусы, косинусы и тангенсы углов треугольника и одну из его сторон, можно найти остальные.
Мы тоже нарисуем таблицу значений синуса, косинуса, тангенса и котангенса для «хороших» углов от до .
| 0 | |||||
| sin | 0 | ||||
| cos | 0 | ||||
| tg | 0 | − | |||
| ctg | − | 0 |
Обратите внимание на два прочерка в таблице. При соответствующих значениях углов тангенс и котангенс не существуют.
При соответствующих значениях углов тангенс и котангенс не существуют.
Докажем теорему:
Если острый угол одного прямоугольного треугольника равен острому углу другого прямоугольного треугольника, то синусы этих углов равны, косинусы этих углов равны и тангенсы этих углов равны.
В самом деле, пусть АВС и — два прямоугольных треугольника с прямыми углами С и и равными острыми углами А и
Треугольники АВС и подобны по первому признаку подобия треугольников, поэтому
Из этих равенств следует, что т. е. sin А = sin
Аналогично, т. е. cos А = cos и т. е. tg A = tg
Это значит, что синус, косинус и тангенс зависят только от величины угла.
Разберем несколько задач по тригонометрии из Банка заданий ФИПИ.
Задача 1. В треугольнике ABC угол C равен , sin A = 0,1. Найдите cos B.
Задача решается за четыре секунды.
Поскольку , sin A = cos B = 0,1.
Задача 2. В треугольнике угол равен , , .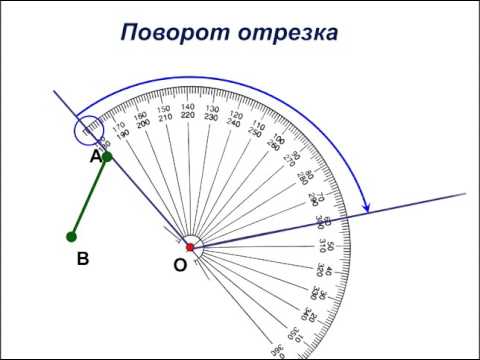
Найдите .
Решение:
Отсюда
Найдем AC по теореме Пифагора.
Ответ: 4,8.
Задача 3. В треугольнике АВС угол С равен AВ = 13, ВС = 5. Найдите косинус и тангенс острого угла А. Ответ округлите до сотых.
Решение:
Для угла А противолежащий катет – это ВС,
АВ является гипотенузой треугольника, лежит против Значит, sin A
Катет, прилежащий к – это катет АС, следовательно, cos А
Длину катета АС найдем по теореме Пифагора:
Тогда
cos А
tg A
Ответ: 0,92; 0,42.
Заметим, что если катеты прямоугольного треугольника равны 5 и 12, то гипотенуза равна 13. Это одна из так называемых Пифагоровых троек. О них мы расскажем в других статьях сайта.
Задача 4. В треугольнике АВС угол С равен AC = 2, sin A=
Найдите BC.
Решение:
AC = b = 2, BC = a, AB = c.
Так как sin A
По теореме Пифагора получим
Ответ: 0,5.
Задача 5. В треугольнике АВС угол С равен tg A = Найдите AB.
Решение:
AC = b = 4, tg A
Ответ: 7.
Задача 6.
В треугольнике АВС угол С равен CH – высота, AB = 13, tg A = Найдите AH.
Решение:
AВ = с = 13, tg A = тогда b = 5a.
По теореме Пифагора ABC:
тогда
(по двум углам), следовательно откуда
Ответ: 12,5.
Задача 7. В треугольнике АВС угол С равен
CH – высота, BC = 3, sin A =
Найдите AH.
Решение:
Так как sin A = тогда c = АВ = 18.
sin A = = cos B =
Рассмотрим BHC:
= получим
тогда BH = = 0,5,
AH = AB — BH = 18 — 0,5 = 17,5.
Ответ: 17,5.
Задача 8. В треугольнике АВС угол С равен 90 CH — высота, BC = 3, cos A =
Найдите АH.
Решение:
Так как для АВС: A = sin В =
а для ВНС: sin В = = , откуда СН =
По теореме Пифагора найдем ВН:
Высота прямоугольного треугольника, проведенная из вершины прямого угла, есть среднее пропорциональное между отрезками, на которые делится гипотенуза этой высотой.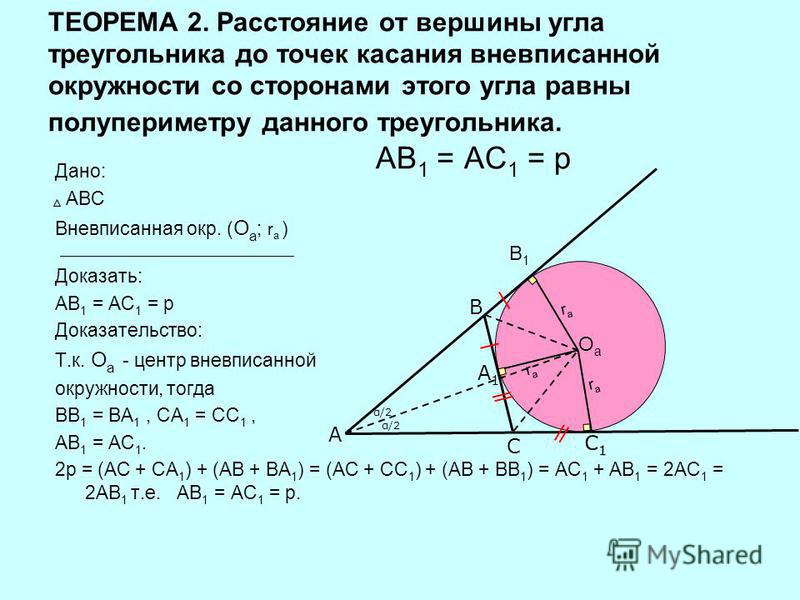 Поэтому для АВС получим:
Поэтому для АВС получим:
тогда
Ответ: 17,5.
Задача 9. В треугольнике АВС угол С равен 90 CH — высота, СН = 24 и BН = 7. Найдите sin A.
Решение:
По определению sin A= = =
Рассмотрим BHC :
ВС найдем по теореме Пифагора:
ВС=
тогда а значит и sin A = = 0,28.
Ответ: 0,28.
Задача 10. В треугольнике АВС угол С равен 90 CH — высота, СН = 8 и BН = 4. Найдите tg A.
Решение:
По определению sin A = = = cos A = = =
тогда tg A = который найдем из BHC:
Ответ: 0,5.
Задача 11. В треугольнике АВС угол С равен 90 CH — высота, BН = 12, tg A = Найдите АН.
Решение:
По определению tg A=
Для BHC: , значит СН =
Для АHC: tg A= то AH =
Ответ: 27.
Задача 12. В треугольнике АВС угол С равен 90 CH — высота, BН = 12, sin A = Найдите АВ.
Решение:
Так как cos В = = sin A =
Из СВН имеем cos В = = тогда ВС =
В АВС имеем sinA = = тогда AВ =
Ответ: 27.
Задача 13. В треугольнике АВС угол С равен 90 из вершины прямого угла к гипотенузе проведена высота СН. Найдите cos A, AC и AB, если СН = 12, ВС = 20.
Решение:
Найдем НВ по теореме Пифагора из ВСН:
sin В = =
Для АВС: cos A = получили cos A = 0,6.
Найдем АС и АВ несколькими способами.
1-й способ.
Так как cos A = то пусть АС = 3х, АВ = 5х,
тогда по теореме Пифагора получим
х = 5 ( так как х0). Значит,
2-й способ.
(по двум углам), значит или
k = тогда АС = ; АВ =
3-й способ.
(высота прямоугольного треугольника, проведенная из вершины прямого угла, есть среднее пропорциональное между отрезками, на которые делится гипотенуза этой высотой) , тогда АН = 144:16 = 9.
АВ = АН + НВ = 9 + 16 = 25.
По теореме Пифагора найдем АС:
=
Ответ: cos A = 0,6; АС = 15, АВ = 25.
Задача 14.
Высота ВН прямоугольного треугольника АВС, проведенная из вершины прямого угла В, равна 24 и отсекает от гипотенузы АС отрезок НС, равный 18.
Найдите АВ и cos А.
Решение:
Из прямоугольного ВНС по теореме Пифагора найдем гипотенузу ВС и cos C:
ВС = =
cos C =
Для АВС: sin А = = cos C =
Для АНВ: sin А = = то = АВ =
Из основного тригонометрического тождества найдем
cos A =
Ответ: АВ = 40, cos A = 0,8.
Задача 15.
Гипотенуза АС прямоугольного треугольника АСЕ равна 50, sin А =
Найдите площадь треугольника.
Решение:
В прямоугольном АСЕ sin А =
значит = 14.
Второй катет найдем, используя теорему Пифагора:
Площадь прямоугольного треугольника равна S =
поэтому
Ответ: 336.
Задача 16.
В треугольнике АВС угол С — прямой, катеты АВ = 13 и ВС = 12, СК — высота.
Найдите sin Результат округлите до сотых.
Решение:
A-общий, ),
значит sin
Найдем АС по теореме Пифагора из САВ:
Тогда sin
Ответ: 0,38.
Задача 17. В треугольнике АВС АС = ВС, АВ = 72, cos A = Найдите высоту СН.
Решение:
Так как АС = ВС, то АВС — равнобедренный с основанием АВ, тогда
высота СН является медианой, то есть АН = НВ =
Поскольку АСН — прямоугольный,
cos A = то есть АС =
По теореме Пифагора тогда
Ответ: 15.
Задача 18. В треугольнике АВС угол С равен 90 sin A = AC = 10 Найдите АВ.
Решение:
1-й способ.
Поскольку sin A = то можно обозначить
ВС = 11х, АВ = 14х.
По теореме Пифагора
(14х- 11х)(14х + 11х) = 3 100;
учитывая, что длина стороны положительна, х = 2,
следовательно, АВ = 14 2 = 28.
2-й способ.
Воспользуемся основным тригонометрическим тождеством
cos A =
По определению cos A = значит
Так как АС=10 то откуда АВ = = 28.
Ответ: 28.
Задача 19. Найдите углы ромба АВСD, если его диагонали АС и ВD равны 4 и 4.
Решение:
Пусть ВАО =
Диагонали ромба делят его углы пополам, значит, =
Диагонали ромба взаимно перпендикулярны и точкой пересечения делятся пополам, следовательно, в прямоугольном треугольнике АВО катет АО = а катет ВО =
Поэтому tg откуда
Ответ:
Часто в задачах встречаются треугольники с углами и или с углами и . Основные соотношения для них запоминайте наизусть!
Для треугольника с углами и катет, лежащий напротив угла в , равен половине гипотенузы.
Треугольник с углами и — равнобедренный. В нем гипотенуза в раз больше катета.
Задача 20.
В треугольнике АВС угол С равен 90 угол А равен 30 АВ = 2
Найдите высоту CH.
Решение:
Рассмотрим АВС:
По свойству катета, лежащего против угла имеем ВС = АВ =
В BHC: то следовательно, ВН = BC =
По теореме Пифагора найдем НС:
Ответ: 1,5.
Задача 21.
В треугольнике АВС угол С равен 90 CH — высота, АВ = 2, Найдите АH.
Решение:
Из АВС найдем ВС = АВ = 1 (по свойству катета, лежащего против угла 30),
то
Из ВСН: то следовательно,
ВН = ВС =
АН = АВ — НВ = 2 — = 1,5.
Ответ: 1,5.
Еще раз повторим, что такое синус, косинус и тангенс угла в прямоугольном треугольнике.
Как запомнить эти соотношения? Лучший способ – решать много задач, и на уроках геометрии, и готовясь к ЕГЭ. Тогда все формулы, равенства, соотношения запомнятся сами собой.
Мы рассмотрели задачи на решение прямоугольных треугольников — то есть на нахождение неизвестных сторон или углов. Но это не всё! В вариантах ЕГЭ по математике множество задач, где фигурирует синус, косинус, тангенс или котангенс внешнего угла треугольника. Об этом — в следующей статье.
Если вам понравился разбор данной темы — записывайтесь на курсы подготовки к ЕГЭ по математике онлайн
Спасибо за то, что пользуйтесь нашими статьями.
Информация на странице «Синус, косинус и тангенс острого угла прямоугольного треугольника» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.
Публикация обновлена:
09.03.2023
Теорема косинусов и синусов треугольника. Формулы и примеры
Поможем понять и полюбить математику
Начать учиться
224.7K
9 класс — насыщенное новыми знаниями время. Чтобы не запутаться в теории по геометрии, рекомендуем сделать карточки с информацией по каждой теме. В этой статье вы найдете самое важное про теорему косинусов.
Формулировка и доказательство теоремы косинусов
Для начала вспомним теорему Пифагора: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
Формула Теоремы Пифагора:
a2> + b2> = c2>, где a, b — катеты, с — гипотенуза.
Теорема косинусов звучит так: квадрат стороны треугольника равен сумме квадратов двух других его сторон минус удвоенное произведение этих сторон на косинус угла между ними. Формула теоремы косинусов: a2 = b2 + c2 — 2bc cos α |
В доказательстве теоремы косинусов используем формулу длины отрезка в координатах.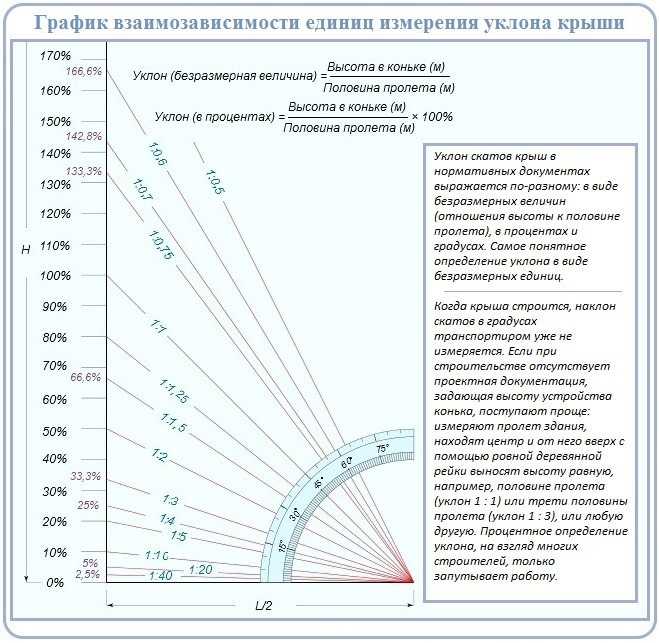 Рассмотрим данную формулу:
Рассмотрим данную формулу:
BC2 = (x2 — x1)2 + (y2 — y1)2
В доказательстве теоремы косинусов BC — это сторона треугольника АВС, которая обозначена буквой а. Введем удобную систему координат и найдем координаты нужных нам точек. У точки В координаты (с; 0).
Координаты точки С — (b cos α; b sin α) при α ∈ (0° ; 180°).
cos2α + sin2α = 1 — основное тригонометрическое тождество.
BC2 = a2 = (b cos α — c)2 + b2sin2α = b2cos2α + b2sin2α — 2bc cos α + c2 = b2(cos2α + sin2α) — 2bc cos α + c2
Что и требовалось доказать.
Совет: чтобы быстрее разобраться в сложной теме, запишитесь на
онлайн-курсы по математике для детей и подростков.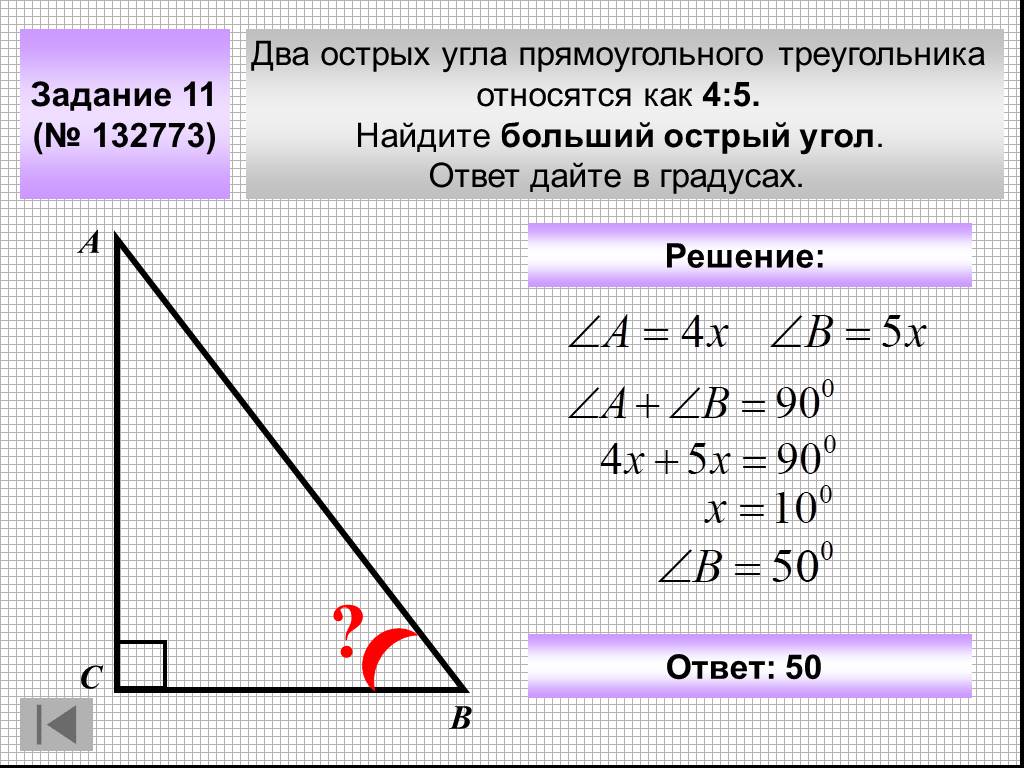
С помощью теоремы косинусов можно найти косинус угла треугольника:
- Когда b2 + c2 — a2 > 0, угол α будет острым.
- Когда b2 + c2 — a2 = 0, угол α будет прямым.
- Когда b2 + c2 — a2 < 0, угол α будет тупым.
Запоминаем
Когда угол α прямой, то теорема косинусов превращаеся в теорему Пифагора.
Сформулируем еще одно доказательство теоремы косинусов.
Пусть нам дан треугольник ABC, в котором из вершины C на сторону AB опустили высоту CD. Это значит:
- AD = b × cos α,
- DB = c – b × cos α.
Запишем теорему Пифагора для двух прямоугольных треугольников ADC и BDC:
- h2 = b2 — (b × cos α)2
- h2 = a2 — (c – b × cos α)2
Приравниваем правые части уравнений:
- b2 — (b × cos α)2 = a2 — (c — b × cos α)2
либо
- a2 = b2 + c2 — 2bc × cos α
Если один из углов при основании тупой (высота упирается в продолжение основания), полностью аналогичен рассмотренному выше.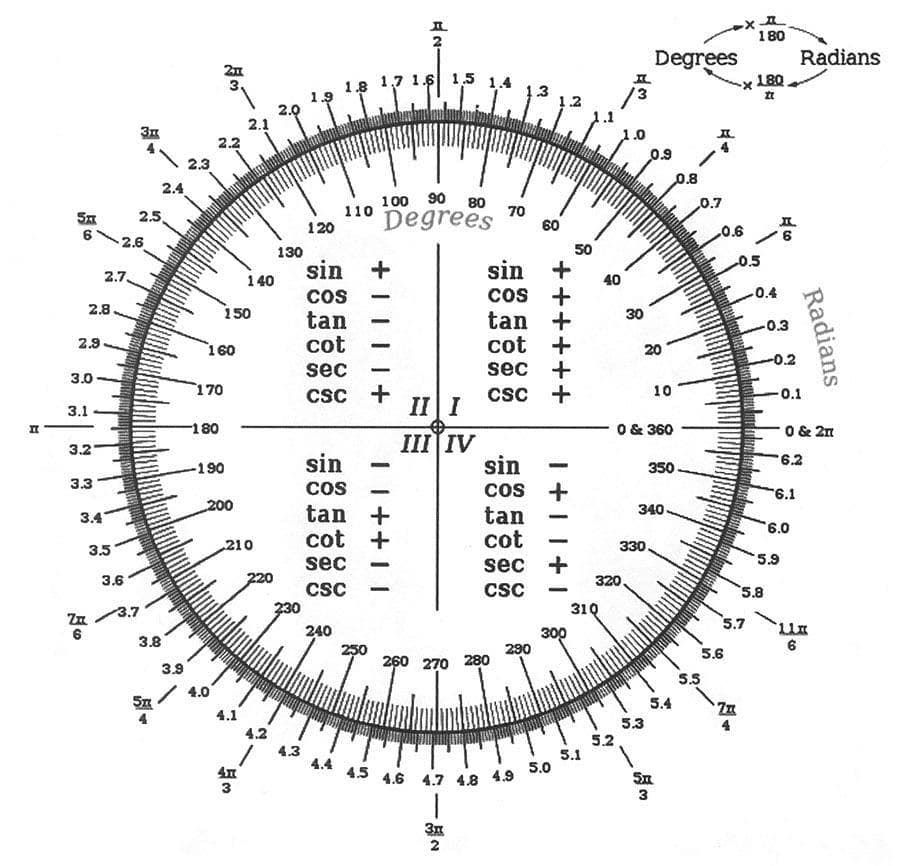
Определим стороны b и c:
- b2 = a2 + c2 — 2ac × cos β;
- c2 = a2 + b2 — 2ab × cos γ.
Реши домашку по математике на 5.
Подробные решения помогут разобраться в самой сложной теме.
Формулировка теоремы для каждой из сторон треугольника
Теорема косинусов справедлива для всех сторон треугольника, то есть:
a2 = b2 + c2 — 2bc cos α
b2 = c2 + a2 — 2ca cos β
c2 = a2 + b2 — 2ab cos γ
Теорема косинусов может быть использована для любого вида треугольника.
Косинусы углов треугольника
Теорема косинусов позволяет найти как косинус, так и угол треугольника. Найдём косинусы углов:
Найдём косинусы углов:
Аналогично:
Определение угла с помощью косинуса
А теперь обратим внимание на углы.
Как мы уже знаем, косинус угла из промежутка (0°; 180°) определяет угол (в отличие от его синуса).
Пусть нам дана единичная полуокружность. Если нам задан cos α, то нам задана точка на верхней полуокружности и задан угол α. Следовательно, cos α однозначно определяет точку М(cos α; sin α), и однозначно определяется угол ∠AOM.
Рассмотрение пределов изменения cos α и sin α
Рассмотрим пределы изменения синуса и косинуса α. Вспомним, что если α — угол треугольника, то он лежит в пределах от 0° до 180°.
Предел изменения косинуса: -1 < cos α < 1.
Предел изменения синуса: 0 < sin α ≤ 1.
- Если cos α > 0, то α ∈ (0°;90°)
- Если cos α < 0, то α ∈ (90°;180°)
- Если cos α = 0, то α = 90°
Примеры решения задач
При помощи теоремы косинусов можно решать задачки по геометрии. Рассмотрим интересные случаи.
Рассмотрим интересные случаи.
Пример 1. Дан треугольник АВС. Найти длину СМ.
∠C = 90°, АВ = 9, ВС = 3, AM/MB = 1/2, где М — точка на гипотенузе АВ.
Как решаем:
- Так как АМ + МВ = 9, а AM/MB = 1/2, то АМ = 3, МВ = 6.
Из треугольника АВС найдем cos B: - Из треугольника СМВ по теореме косинусов найдём СМ:
Ответ: СМ = .
Пример 2. Дан треугольник АВС, в котором a2 + b2 < c2. Доказать, что ∠C — тупой угол.
Как доказываем:
- Для доказательства нужно вспомнить теорему косинусов для угла ∠C:
- Так как a2 + b2 < c2, то cos C < 0, следовательно, ∠C — тупой.

Что и требовалось доказать.
Эта задача нам показала, что с помощью теоремы косинусов можно определить тупой угол или острый.
- Если c2 = a2 + b2, то ∠C = 90°.
- Если c2 < a2 + b2, то ∠C — острый.
Больше объяснений по этой и другим темам вы найдете в справочнике по математике — с формулами, чертежами и примерами решения задач.
Шпаргалки для родителей по математике
Все формулы по математике под рукой
Лидия Казанцева
Автор Skysmart
К предыдущей статье
Теоремы, которые точно пригодятся на ЕГЭ
К следующей статье
149.2K
Векторное произведение векторов
Получите план обучения, который поможет понять и полюбить математику
На вводном уроке с методистом
Выявим пробелы в знаниях и дадим советы по обучению
Расскажем, как проходят занятия
Подберём курс
Калькулятор опорного угла
| Квадранты графика
Базовый угол для 1°: 1°
Базовый угол для 2°: 2°
Базовый угол для 3°: 3°
Базовый угол для 4°: 4°
Базовый угол для 5°: 5°
Базовый угол для 6°: 6°
Базовый угол для 7°: 7°
Базовый угол для 8°: 8°
Базовый угол для 9°: 9°
Базовый угол для 10°: 10°
Базовый угол для 15°: 15°
Базовый угол для 20°: 20°
Базовый угол для 25°: 25°
Базовый угол для 30°: 30° (π / 6)
Базовый угол для 35°: 35°
Базовый угол для 40°: 40°
Базовый угол для 45°: 45° (π / 4)
Базовый угол для 50°: 50°
Базовый угол для 55°: 55°
Базовый угол для 60°: 60° (π / 3)
Базовый угол для 65°: 65°
Базовый угол для 70°: 70°
Базовый угол для 75°: 75°
Базовый угол для 80°: 80°
Опорный угол для 85°: 85°
Базовый угол для 90°: 90° (π / 2)
Базовый угол для 95°: 85°
Базовый угол для 100°: 80°
Базовый угол для 105°: 75°
Базовый угол для 110°: 70°
Базовый угол для 115°: 65°
Опорный угол для 120°: 60° (π / 3)
Базовый угол для 125°: 55°
Базовый угол для 130°: 50°
Базовый угол для 135°: 45° (π / 4)
Базовый угол для 140°: 40°
Базовый угол для 145°: 35°
Базовый угол для 150°: 30° (π / 6)
Базовый угол для 155°: 25°
Базовый угол для 160°: 20°
Базовый угол для 165°: 15°
Базовый угол для 170°: 10°
Базовый угол для 175°: 5°
Базовый угол для 180°: 0°
Базовый угол для 185°: 5°
Базовый угол для 190°: 10°
Базовый угол для 195°: 15°
Базовый угол для 200°: 20°
Базовый угол для 205°: 25°
Базовый угол для 210°: 30° (π / 6)
Базовый угол для 215°: 35°
Базовый угол для 220°: 40°
Базовый угол для 225°: 45° (π / 4)
Базовый угол для 230°: 50°
Базовый угол для 235°: 55°
Опорный угол для 240°: 60° (π / 3)
Базовый угол для 245°: 65°
Базовый угол для 250°: 70°
Базовый угол для 255°: 75°
Базовый угол для 260°: 80°
Базовый угол для 265°: 85°
Базовый угол для 270°: 90° (π / 2)
Базовый угол для 275°: 85°
Опорный угол для 280°: 80°
Базовый угол для 285°: 75°
Базовый угол для 290°: 70°
Базовый угол для 295°: 65°
Базовый угол для 300°: 60° (π / 3)
Базовый угол для 305°: 55°
Базовый угол для 310°: 50°
Базовый угол для 315°: 45° (π / 4)
Базовый угол для 320°: 40°
Базовый угол для 325°: 35°
Базовый угол для 330°: 30° (π / 6)
Базовый угол для 335°: 25°
Базовый угол для 340°: 20°
Базовый угол для 345°: 15°
Базовый угол для 350°: 10°
Базовый угол для 355°: 5°
Опорный угол для 360°: 0°
Калькулятор опорного угла | Pi Day
Чтобы использовать калькулятор опорного угла , , просто введите любой угол в поле угла, чтобы найти его опорный угол, который является острым углом, соответствующим введенному углу. Калькулятор автоматически применяет правила, которые мы рассмотрим ниже.
Калькулятор автоматически применяет правила, которые мы рассмотрим ниже.
Базовый угол
Вернуться на страницу калькуляторов
Что такое базовый угол?
Представьте координатную плоскость. Допустим, мы хотим нарисовать угол в 144° на нашей плоскости. Мы начинаем с правой стороны оси X, где три часа на часах. Мы вращаем против часовой стрелки, которая начинается с движения вверх. Мы продолжаем идти мимо 90° (верхняя часть оси Y), пока не дойдем до 144°. Проводим луч из начала координат, являющегося центром плоскости, в эту точку. Теперь у нас есть луч, который мы называем конечной стороной. Но нам нужно нарисовать еще один луч, чтобы получился угол. На данный момент у нас есть выбор. Наш второй луч должен быть на оси X. Если мы нарисуем его из начала координат вправо, мы нарисуем угол, равный 144°. Если мы нарисуем его влево, мы нарисуем угол, равный 36°. Этот второй угол является опорным углом. Это всегда меньший из двух углов, он всегда будет меньше или равен 9. 0°, и он всегда будет положительным. Вот анимация, которая показывает опорный угол для четырех разных углов, каждый из которых находится в другом квадранте. Обратите внимание, что второй луч всегда находится на оси x.
0°, и он всегда будет положительным. Вот анимация, которая показывает опорный угол для четырех разных углов, каждый из которых находится в другом квадранте. Обратите внимание, что второй луч всегда находится на оси x.
Чем полезен эталонный угол?
Опорный угол всегда имеет те же значения триггерной функции, что и исходный угол. Обратите внимание, что слово имеет значение . Знак может не совпадать, но значение всегда будет. Это полезно для распространенных углов, таких как 45° и 60°, с которыми мы будем сталкиваться снова и снова. Зная их значения синуса, косинуса и тангенса, мы также знаем значения любого угла, опорный угол которого также равен 45° или 60°. Что касается знака, помните, что синус положителен в 1-м и 2-м квадранте, а косинус положителен в 1-м и 4-м квадранте.
Как найти опорный угол без калькулятора?
То, как мы находим опорный угол, зависит от квадранта конечной стороны.
Когда крайняя сторона находится в первом квадранте (углы от 0° до 90°), наш исходный угол совпадает с нашим заданным углом. Это имеет смысл, так как все углы в первом квадранте меньше 90°. Итак, если наш заданный угол равен 33°, то его опорный угол также равен 33°.
Это имеет смысл, так как все углы в первом квадранте меньше 90°. Итак, если наш заданный угол равен 33°, то его опорный угол также равен 33°.
Когда крайняя сторона находится во втором квадранте (углы от 90° до 180°), наш опорный угол равен 180° минус заданный угол. Итак, если наш заданный угол равен 110°, то его исходный угол равен 180° – 110° = 70°.
Когда крайняя сторона находится в третьем квадранте (углы от 180° до 270°), наш исходный угол равен заданному углу минус 180°. Итак, если наш заданный угол равен 214°, то его исходный угол равен 214° – 180° = 34°.
Когда клеммная сторона находится в положении четвертый квадрант (углы от 270° до 360°), наш опорный угол равен 360° минус заданный угол. Итак, если наш заданный угол равен 332°, то его опорный угол равен 360° – 332° = 28°.
Что, если наш угол больше 360°?
Когда угол больше 360°, это означает, что он повернулся вокруг координатной плоскости и продолжает движение. Чтобы найти его опорный угол, нам сначала нужно найти соответствующий ему угол между 0° и 360°. Это легко сделать. Мы просто продолжаем вычитать из него 360, пока оно не станет меньше 360. Например, если наш угол равен 544°, мы должны вычесть из него 360°, чтобы получить 184° (544° – 360° = 184°). Теперь мы заметим, что он находится в третьем квадранте, поэтому мы должны вычесть из него 180 °, чтобы найти, что наш опорный угол равен 4 °.
Чтобы найти его опорный угол, нам сначала нужно найти соответствующий ему угол между 0° и 360°. Это легко сделать. Мы просто продолжаем вычитать из него 360, пока оно не станет меньше 360. Например, если наш угол равен 544°, мы должны вычесть из него 360°, чтобы получить 184° (544° – 360° = 184°). Теперь мы заметим, что он находится в третьем квадранте, поэтому мы должны вычесть из него 180 °, чтобы найти, что наш опорный угол равен 4 °.
Что, если наш угол отрицательный?
Когда угол отрицательный, мы двигаемся в другом направлении, чтобы найти нашу конечную сторону. Это означает, что при рисовании мы движемся по часовой стрелке, а не против часовой стрелки. Или мы можем рассчитать его, просто прибавив к 360°. Например, если наш заданный угол равен –110°, то мы должны добавить его к 360°, чтобы найти положительный угол в 250° (–110° + 360° = 250°). Теперь нам нужно увидеть, что мы находимся в третьем квадранте, и применить это правило, чтобы найти исходный угол (250° – 180° = 70°).

 Аналогично,
Аналогично,