Дебит нефти или газа — Что такое Дебит нефти или газа?
ИА Neftegaz.RU.
Дебит нефти или газа — объем нефти или газа, поступающих в единицу времени из естественного или искусственного источника (колодца, буровой скважины и тд).
Дебит является характеристикой источника (буровой скважины, трубы, колодца и тд), определяющей его способность генерировать продукт, при заданном режиме эксплуатации, зависящей от его связей с прилегающими нефте-, газо- или водоносными слоями, истощения этих слоёв, а также сезонных колебаний (для грунтовых вод).
Дебит скважины — объем продукции, добываемой из скважины за единицу времени (секунду, сутки, час и др.).
Может характеризовать добычу нефти, газа, газового конденсата, воды.
Используются понятия:
-
дебит конкретной скважины, - средний дебит скважины (рассчитывается как суточная добыча группы скважин (месторождения, объекта разработки) по отношению к количеству добывающих скважин).

Дебит нефтяных скважин измеряется в м³ либо т/единицу времени (м³/час, м³/сутки).
Дебит газовых скважин измеряется в 1000 м³/единицу времени (тыс м³/час, тыс м³/сутки).
Дебит газоконденсатных скважин измеряется в т/единицу времени (т/час, т/сутки).
Дебит водных скважин измеряется в м³/единицу времени (м³/с, м³/час, м³/сутки).
Используются понятия: дебит конкретной скважины; средний дебит скважины (рассчитывается как суточная добыча группы скважин (месторождения, объекта разработки) по отношению к количеству добывающих скважин).
Дебит характеризует устойчивое поступление жидкости или газа в течение длительного времени.
Объём воды, протекающий в единицу времени через поперечное сечение реки или водоносного горизонта, называется расходом воды.
Дебит применяют для измерения объёма воды, получаемого при искусственной откачке воды из колодцев и скважин, в процессе которой подаваемое количество жидкости зависит от способа и интенсивности откачки и понижения её уровня.
Для характеристики производительности водозаборных скважин служит удельный дебит (отнесённый к понижению уровня воды при откачке на 1 м).
Дебит скважины зависит от проницаемости и мощности продуктивного горизонта , условий его питания, распространения и взаимосвязи с другими горизонтами, наличия напора и прочего, а также от условий эксплуатации продуктивного горизонта, степени его вскрытия, понижения уровня нефти или газа при откачке и других факторов.
Различают установившийся и неустановившийся дебит, так как в 1е время можно получить завышенное значение дебита, особенно если вскрыта нефть, заключающая большое количество газов.
На основе наблюдений за дебита нефтяных скважин строят кривые, показывающие изменения дебита в процессе эксплуатации.
Анализируя эти кривые, определяют промышленные категории запасов нефти.
Этот метод кривых основан на статистическом учёте добычи нефти за определенные периоды времени.
По кривой зависимости дебита от времени с помощью математических расчётов устанавливают коэффициент падения дебита, который служит основой подсчёта запасов нефти по группам скважин и по пласту в целом.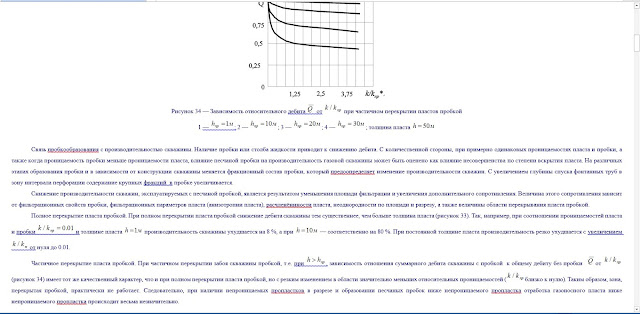
Дебит скважины обязателен к подсчету как для определения параметров насосной установки, так и выбора остального оборудования скважин.
Существует всего методы для подсчета дебита скважин нефтяного месторождения — стандартный и по Дюпюи:
Расчет по стандартной формуле:
D = H x V/(Hд – Hст),
H — Высота водного столба;
V — Производительность насоса;
Hд, Hст — статический и динамический уровень.
Статический уровень в этом случае – расстояние от начала подземных вод до первых слоев почвы, а динамический уровень — абсолютная величина, получаемая при замере уровня воды после откачивания.
Оптимальный показатель дебита нефтяного месторождения определяется, как для общего установления уровня депрессии отдельной скважины, так и всего пласта в целом.
Формула высчитывания среднего уровня депрессии месторождения определяется, как Р заб=0.
Дебит 1й скважины, который был получен при оптимальной депрессии, и будет являться оптимальным дебитом нефтяной скважины.
Из-за механического и физического давления на пласт, может происходить обрушение части внутренних стенок нефтяных скважин, поэтому приходится уменьшать потенциальный дебит механическим способом, чтобы сохранить бесперебойность процесса добычи нефти и сохранения прочности стенок.
Расчет по формуле Дюпюи:
1. Идеальный случай:
N0 = kh/ub * 2Pi/ln(Rk/Rc), где
N0 – потенциальная продуктивность;
Kh/u – коэффициент, определяющий свойство гидропроводности нефтяного пласта;
B – коэффициент расширения по объему;
Pi – Число П = 3,14…;
Rk – радиус контурного питания;
Rc – долотный радиус скважины по расстоянию до вскрытого пласта.
2. Расчет для фактической продуктивности месторождения:
N = kh/ub * 2Pi/(ln(Rk/Rc)+S).
N – фактическая продуктивность;
S – скин-фактор (параметр фильтрационного сопротивления течению).
4. Расчет дебита нефтяной скважины
Общее уравнение
притока жидкости в скважину имеет вид
где Q — дебит
скважины; k
— размерный коэффициент пропорциональности;
n
— показатель степени, характеризующий
режим движения жидкости (фильтрации).
Прил
=
1 выражение
(2.61) записывается так:
где КПР
— коэффициент продуктивности скважины,
т/ (сут·МПа) (стандартные условия).
Дебит несовершенной
скважины в условиях плоскорадиального
притока в соответствии с формулой Дюпюи
где к — проницаемость
пласта (призабойной зоны скважины), м2;
h
— толщина пласта (работающая), м; ηнп
— вязкость нефти в пластовых условиях,
мПа·с; rПР
— приведенный радиус скважины, м;
RК
— радиус контура питания, м.
Из сопоставления
(2. 62) и (2.63) получаем
62) и (2.63) получаем
где bН
— объемный коэффициент нефти; ρНП
— плотность нефти в пластовых условиях,
кг/м3.
В соответствии
с (2.64) дебит скважины в стандартных
условиях, измеряемый в т/сут, можно
рассчитать по следующей формуле:
.
Задача 7.
Вычислить дебит нефтяной скважины при
забойном давлении, равном давлению
насыщения, для следующих условий:
проницаемость
призабойной зоны 0,25 мкм2;
толщина пласта h,
м; плотность нефти в пластовых условиях
ρНП
кг/м3;
вязкость нефти в пластовых условиях 2
мПа·с; плотность дегазированной нефти
ρНД
кг/м3;
радиус контура питания RК
м; приведенный радиус скважины 0,01 м;
пластовое давление pПЛ
МПа; газосодержание (газонасыщенность)
пластовой нефти (объем газа приведен к
стандартным условиям) S0
м3/м3,
давление насыщения при t = 20 °С РНАС20
= 8,48 МПа; пластовая температура 82 °С;
содержание метана в газе однократного
разгазирования при стандартных условиях
Ум =
0,622, а азота Уа
= 0,027.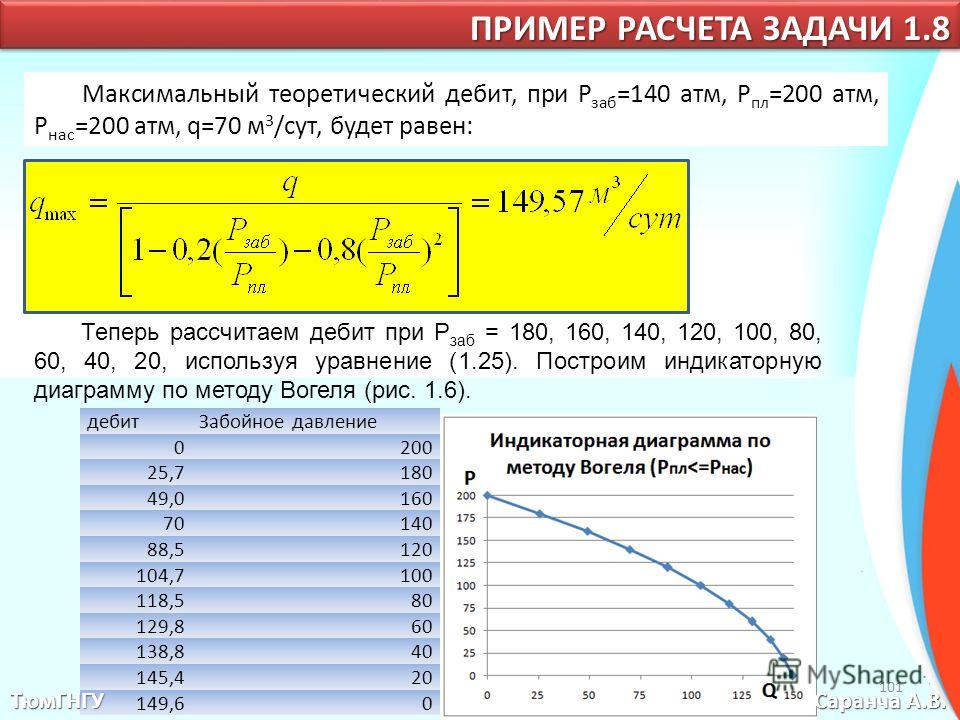
Наименование | Последняя цифра | |||||||||
0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
h, | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
ρНП | 800 | 801 | 802 | 803 | 804 | 805 | 806 | 807 | 808 | 809 |
ρНД | 850 | 851 | 852 | 853 | 854 | 855 | 856 | 857 | 858 | 859 |
pПЛ, | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 |
S0 | 78,0 | 78,1 | 78,2 | 78,3 | 78,4 | 78,5 | 78,6 | 78,7 | 78,8 | 78,9 |
Пример:
h=5
м, ρНП=805
кг/м3,
ρНД=862
кг/м3,
pПЛ=25
МПа, S0=78,5
м3/м3.
Указание для
решения задачи.
Прежде всего рассчитываем объемный
коэффициент нефти
где S0
— газонасыщенность пластовой нефти
м3/м3
(объем газа приведен к стандартным
условиям).
Затем определяем
давление насыщения при пластовой
температуре, так как в исходных данных
оно дано при стандартной температуре.
Для этого:
.
Приводим заданное
газосодержание S0
пластовой нефти к размерности Sом
в вышеприведенном уравнении.
Для этого :
Тср
=273+ t
(К)
ТО
= 273(К)
Таким образом,
давление насыщения при tПЛ
МПа,
Рассчитываем дебит
скважины
Q≈295.3
т/сут.
Расчетный дебит
в стандартных условиях составляет 295,3
т/сут.
Основы течения флюида — AAPG Wiki
Расчеты потока в скважине в основном сосредоточены на двух аспектах течения флюида: профиле давления вдоль пути потока и зависимости дебита от давления в ключевых представляющих интерес точках (узлах), как показано на рисунке 1. интересующие параметры (все в единицах фунтов на квадратный дюйм)
- p R = пластовое давление
- p wf = скважинное (забойное) гидродинамическое давление
- p wh = устьевое давление
- p sp = давление сепаратора
- p ST = давление в баке
Соответствующие ставки
- q o = дебит нефти (стб/сутки)
- q г = дебит газа (стандартные кубические футы/день)
Разность давлений ( p R – p wf ) называется просадкой водохранилища . Это основная сила, направляющая пластовые флюиды в ствол скважины. Как правило, производительность увеличивается с увеличением просадки. Приток в ствол скважины, вызванный депрессией, называется притоком .
Это основная сила, направляющая пластовые флюиды в ствол скважины. Как правило, производительность увеличивается с увеличением просадки. Приток в ствол скважины, вызванный депрессией, называется притоком .
Взаимосвязь между дебитом, измеренным в складском резервуаре, q o , и гидродинамическим давлением на забое, p wf , называется зависимостью производительности притока (1PR) . IPR скважины можно определить непосредственно по данным эксплуатационных испытаний или его можно спрогнозировать по данным коллектора. Независимо от того, представлено ли оно графически или выражено формулой, IPR представляет собой отчет о производительности и широко используется для проектирования и анализа производительности скважин.
Хорошие общие ссылки на поток в резервуарах и скважинах включают Golan and Whitson, [1] Bradley, [2] и Craft et al. [3]
Содержание
- 1 Эмпирические уравнения IPR
- 1.
 1 Уравнение индекса продуктивности для недонасыщенной нефти
1 Уравнение индекса продуктивности для недонасыщенной нефти - 1.2 Уравнения противодавления для насыщенных нефтью и газом скважин
- 1.3 Квадратное уравнение для насыщенных нефтяных и газовых скважин
- 1.4 Ненасыщенное масло с расширенным диапазоном IPR
- 1.
- 2 Расширение закона Дарси
- 3 Радиальный поток
- 3.1 Единицы формулы закона Дарси
- 3.2 Ограниченный вход в ствол скважины (скин-эффект)
- 4 Зависимость теоретического давления от скорости (IPR)
- 4.1 Радиус дренажа
- 4.2 Расширение модели идеальной скважины
- 5 IPR, полученный в результате моделирования коллектора
- 6 Влияние истощения на формулы ПИС
- 7 Влияние стимуляции и повреждения на уравнения IPR
- 8 См. также
- 9 Каталожные номера
- 10 Внешние ссылки
Эмпирические уравнения ПИС[править]
Рисунок 1 Давление в простой производственной системе.
Рисунок 2 Графики многоступенчатых производственных данных.
Было разработано несколько формул IPR для представления поведения притока различных типов скважин. Сопоставление формулы с данными многодебитной добычи (рис. 2) позволяет определить значение характеристических констант в уравнениях, которые, в свою очередь, характеризуют продуктивность скважины. Эмпирические формулы являются основными инструментами для количественной оценки продуктивности скважин и выполнения расчетов добычи.
Уравнение индекса продуктивности для недонасыщенной нефти Уравнение
- qo = J (pR − pwf) {\ displaystyle q _ {\ rm {o}} = J (p _ {\ rm {R}} -p _ {\ rm {wf}})}
Постоянная характеристики связь дебита нефти с депрессией называется индексом продуктивности f и определяется как
- J = qopR−pwf {\ displaystyle J = {\ frac {q _ {\ rm {o}}} {p _ {\ rm {R}} -p _ {\ rm {wf}}}}}
с единицами STB/day/psi. Индекс продуктивности показывает количество баррелей в день, добытое на каждый фунт на квадратный дюйм снижения давления, и, таким образом, отражает производительность или пропускную способность скважины.
Индекс продуктивности показывает количество баррелей в день, добытое на каждый фунт на квадратный дюйм снижения давления, и, таким образом, отражает производительность или пропускную способность скважины.
Когда p wf равно атмосферному давлению, скорость называется абсолютным открытым потоком (AOF) и часто обозначается как q max . AOF является полезным индикатором продуктивности скважины.
Уравнения противодавления для насыщенных нефтяных и газовых скважин[править] 9{n}}
Имеет две характеристические константы: константу противодавления c и показатель степени противодавления n . Показатель степени n представляет собой безразмерное число от 0,5 до 1,0. Он приближается к 1,0 для скважин с низким дебитом и к 0,5 для скважин с очень высоким дебитом. Значения n и c могут быть определены графически из логарифмического графика данных испытаний с несколькими скоростями в виде{2})}{q}}\quad {\mbox{versus}}\quad (A+Bq)}
Ненасыщенная нефть с расширенным диапазоном IPR b
при пластовом давлении выше точки насыщения ( p wf b p
R ), ПИС принимает форму, показанную на рисунке 2d. Его можно представить следующими уравнениями:
Его можно представить следующими уравнениями:
- для pwf> pb, qo = J (pR−pwf) {\ displaystyle {\ mbox {for}} p _ {\ rm {wf}}> p _ {\ rm {b}}, \ quad q _ {\ rm {o}}=J(p_{\rm {R}}-p_{\rm {wf}})} 9{2})}
Расширение закона Дарси[править]
Закон Дарси, первоначально разработанный для потока воды, был расширен для описания течения углеводородных пластовых флюидов (сжимаемых и многофазных).
Для однофазного потока нефти пропорциональная константа, которая связывает скорость потока с перепадами давления в исходном законе Дарси, разбивается на два независимых фактора: проницаемость породы, k , и вязкость жидкости, μ. Для линейной системы потока, это дает
- q=(A/L)(k/μ)Δp{\displaystyle q=(A/L)(k/\mu)\Delta p}
Проницаемость – это свойство породы, которое отражает «легкость», с которой жидкость течет через него. Вязкость является свойством жидкости и отражает сопротивление жидкости течению.
Для многофазного потока присутствие второй фазы в пористой среде снижает кажущуюся проницаемость первой фазы (например, присутствие газа снижает кажущуюся проницаемость нефти). Присутствие каждой фазы в пористой среде количественно определяется насыщенность, S , которая представляет собой отношение объема флюида в данной пористой породе к объему пор породы:
Присутствие каждой фазы в пористой среде количественно определяется насыщенность, S , которая представляет собой отношение объема флюида в данной пористой породе к объему пор породы:
- So = Vo / VpandSg = Vg / Vp {\ displaystyle S _ {\ rm {o}} = V _ {\ rm {o}} / V _ {\ rm {p}} \ quad {\ mbox {and}} \quad S _ {\ rm {g}} = V _ {\ rm {g}}/V _ {\ rm {p}}}
, где
- S o = нефтенасыщенность (доля)
- S г = газонасыщенность (доля)
- V o = объем нефти в данном объеме пор
- В г = объем газа в данном поровом объеме
- V p = объем пор
Рисунок 3 Двухфазная относительная проницаемость.
Кажущаяся или эффективная нефтепроницаемость k eo одной фазы в присутствии второй фазы может быть представлена как произведение двух членов: абсолютной проницаемости, k a , и относительной нефтепроницаемости, к ро :
- keo = ka × kro {\ displaystyle k _ {\ rm {eo}} = k _ {\ rm {a}} \ times k _ {\ rm {ro}}}
Абсолютная проницаемость является свойством породы и, по существу, представляет собой проницаемость, измеренную с одной фазой или при 100% однофазном насыщении. Относительная проницаемость представляет собой безразмерную величину, величина которой находится в диапазоне от 1,0 до 0, в зависимости от насыщенности (рис. 3). Относительные проницаемости измеряются в керновых (петрофизических) лабораториях, и результаты представляются в зависимости от насыщения. Некоторые лаборатории нормализуют значения относительной проницаемости со значениями, отличными от значений однофазного или 100%-ного насыщения, поэтому при интерпретации и использовании представленных данных необходимо соблюдать осторожность.
Относительная проницаемость представляет собой безразмерную величину, величина которой находится в диапазоне от 1,0 до 0, в зависимости от насыщенности (рис. 3). Относительные проницаемости измеряются в керновых (петрофизических) лабораториях, и результаты представляются в зависимости от насыщения. Некоторые лаборатории нормализуют значения относительной проницаемости со значениями, отличными от значений однофазного или 100%-ного насыщения, поэтому при интерпретации и использовании представленных данных необходимо соблюдать осторожность.
Радиальный поток[править]
Рисунок 4 Распределение давления в радиальном резервуаре.
Закон Дарси можно применить к идеальной модели скважины, обеспечивающей постоянный установившийся дебит. Модель предполагает цилиндрический поток в коллекторе, где поток через формацию является горизонтальным, а жидкость движется радиально по направлению к стволу скважины. Он также предполагает постоянную толщину продуктивной зоны, постоянную изотропную проницаемость и идеальную жидкость (однородную несжимаемую жидкость, в которой вязкость не зависит от давления).
Для резервуаров бесконечного размера результатом будет
- p = pwf + qμB2πkhln (r / rw) {\ displaystyle p = p _ {\ rm {wf}} + {\ frac {q \ mu B} {2 \ pi kh}} \ ln (r / r_ {\rm {w}})}
или в полевых единицах,
- p = pwf + 141,2qoμoBokhln (r / rw) {\ displaystyle p = p _ {\ rm {wf}} + {\ frac {141,2q _ {\ rm {o}} \ mu _ {\ rm {o }}B_{\rm {o}}}{kh}}\ln(r/r_{\rm {w}})}
То есть каждому радиусу r соответствует давление p логарифмически возрастает с р (рис. 4).
Распределение давления в радиально ограниченных резервуарах аналогично бесконечному случаю для большей части дренируемого объема. Однако вблизи границ, как показано на рисунке 4, все по-другому.
Единицы формулы закона Дарси Это гибридная система, состоящая из различных метрических, английских и нефтепромысловых единиц. Он использует миллидарси (md) для проницаемости. Другие размеры и единицы в этой системе следующие:
- q o = расход нефти в резервуаре (STB/день или баррелей в резервуаре в день)
- q г = расход газа (стандартные кубические футы в сутки или стандартные кубические футы в сутки)
- μ o = вязкость (сП или сантипуаз)
- B o = объемный коэффициент пласта (баррели RES/STB, или баррели резервуара к баррелям складского резервуара)
- p R = пластовое давление (psi)
- p wf = забойное давление (psi)
- k = проницаемость (мД)
- h = толщина продуктивного пласта (футы)
- r w = радиус ствола скважины (футы)
- r e = радиус дренажа (футы)
Формулы в следующем разделе даны в практических полевых единицах.
Ограниченный вход в ствол скважины (скин-эффект)[править]
Рисунок 5 Скин-эффект.
Фактическое распределение давления в большинстве случаев отличается от идеального распределения давления, полученного для идеальной модели. Следующее дополнительное падение давления в стволе скважины возникает в результате околоскважинных явлений (Рисунок 5):
- Δpskin = pwf (идеальный) − pwf (фактический) {\ displaystyle \ Delta p _ {\ rm {skin}} = p _ {\ rm {wf (идеальный)}} -p _ {\ rm {wf (фактический)} }}
Наиболее важными явлениями обычно являются конвергенция потока из-за ограниченного проникновения в продуктивную зону (частичное проникновение), нарушение проницаемости вблизи ствола скважины (повреждение пласта) и ограничение потока в перфорационных отверстиях.
Удобно выразить Δ p кожи в виде безразмерной величины s , называемой скин-фактором, который линейно пропорционален Δ p кожи :
- Δpskin = 141,2qoμoBokhs {\ displaystyle \ Delta p _ {\ rm {skin}} = {\ frac {141,2q _ {\ rm {o}} \ mu _ {\ rm {o}} B _ {\ rm {o }}}{kh}}s}
Скин-фактор может быть определен из интерпретации ГДИС и может быть легко преобразован в фактический Δ p скин или P wf(actual)*
Теоретическая зависимость давление-дебит (IPR)[править]
Закон Дарси, примененный к модели идеальной скважины, дает уравнение IPR, выраженное в терминах параметров резервуара. {0,5}}
{0,5}}
, где A — площадь дренирования скважины в квадратных футах, а радиус — в футах. Если площадь дренажа указана в акрах, ее необходимо преобразовать в квадратные футы, используя соотношение 1 акр = 43 560 футов 2 .
Расширение модели идеальной скважины[править]
Теоретически полученные уравнения IPR могут быть расширены для включения добычи газа и насыщенной нефти. Для газовых резервуаров низкого давления (менее 2000 фунтов на квадратный дюйм) используется следующее уравнение:
9{2})}{T\mu _{\rm {g}}Z[\ln(r _{\rm {e}}/r _{\rm {w}})-0,75+s]}}}
где
- q g = расход газа (стандартные кубические футы/день)
- T = температура (R° = F° + 460)
- Z = коэффициент сжимаемости газа
- μ г = вязкость газа (сП)
Все остальные параметры имеют те же единицы измерения, что и уравнения потока нефти. Существуют строгие методы, используемые для выражения IPR газовых скважин при пластовом давлении выше 2000 фунтов на квадратный дюйм. Однако уравнение низкого давления подходит для большинства расчетов производительности скважины.
Однако уравнение низкого давления подходит для большинства расчетов производительности скважины.
9{2})}
где срок к ро /мк o Б o оценивается при среднем пластовом давлении, р
и насыщенности.
При использовании этих уравнений следует помнить о двух практических соображениях. Во-первых, в зависимости от размещения скважин значение ln ( r e / r w ) находится в диапазоне от 6,5 до 8. Значение 7 является хорошим приближением для большинства расчетов производительности. Во-вторых, скин-фактор s положителен, когда вход в ствол скважины ограничен скин-эффектом. Отрицательно, если продуктивность лучше, чем предсказывает идеальная радиальная модель (например, в скважинах с стимуляцией или ГРП).
IPR, полученный на основе моделирования коллектора пластовых параметров. Формула, приведенная в нормализованном виде, имеет вид
- qoqmax = 1−0,2 (pwfpR) −0,8 (pwfpR) 2 {\ displaystyle {\ frac {q _ {\ rm {o}}} {q _ {\ rm {max}}}} = 1-0,2 \ left ({\ frac {p _ {\ rm {wf}}} {p _ {\ rm {R}}}} \ right) -0,8 \ left ({\ frac {p _ {\ rm {wf}}} {p _ {\ пм {R}}}}\вправо)^{2}}
Эта формула полезна для низкодебитных нефтяных скважин. Он завышает продуктивность высокодебитных скважин (производящих более 2000 баррелей в сутки).
Он завышает продуктивность высокодебитных скважин (производящих более 2000 баррелей в сутки).
Пример:
Скважина в резервуаре с растворенным газом имеет пластовое давление 4000 фунтов на квадратный дюйм. Одна контрольная точка равна q o = 200 STB/день с p wf = 3220 фунтов/кв. Подстановка данных в уравнение IPR и решение для q max дает
9{2}}}=624{\mbox{ STP/день}}}
Подстановка рассчитанного q max и заданного p R в уравнение вычисляет баллы по IPR следующим образом:
| pwf (псиа) | qo (STB/день) |
|---|---|
| 4000 | 0 |
| 3000 | 250 |
| 2000 | 437 |
| 1500 | 508 |
| 1000 | 562 |
Влияние истощения на формулы ПИС
Истощение обычно приводит к ухудшению IPR (рис. 6). Эти изменения можно предсказать количественно, рассчитав изменения характеристических констант: j , c , q ax A и B . Показатель степени n не меняется при истощении. Если индекс p обозначает текущее состояние истощения, а нижний индекс f — будущее состояние, настоящий и будущий характерные факторы связаны следующим образом:
6). Эти изменения можно предсказать количественно, рассчитав изменения характеристических констант: j , c , q ax A и B . Показатель степени n не меняется при истощении. Если индекс p обозначает текущее состояние истощения, а нижний индекс f — будущее состояние, настоящий и будущий характерные факторы связаны следующим образом:
Для резервуаров с недонасыщенной нефтью:
- JfJp = (μoBo) p (μoBo) f {\ displaystyle {\ frac {J _ {\ rm {f}}} {J _ {\ rm {p}}}} = {\ frac {(\ mu _ { \ rm {o}} B _ {\ rm {o}}) _ {\ rm {p}}} {(\ mu _ {\ rm {o}} B _ {\ rm {o}}) _ {\ rm { f}}}}}
Газовые резервуары низкого давления:
- cf = cpandnf = np {\ displaystyle c _ {\ rm {f}} = c _ {\ rm {p}} \ quad {\ mbox {and}} \ quad n _ {\ rm {f}} = n_ { \гт {р}}} 9{n}}
, где
- qo max=480 STB/день{\displaystyle q_{\rm {o\ max}}=480{\mbox{STB/день}}}
- pR = 4000 фунтов на квадратный дюйм {\ displaystyle p _ {\ rm {R}} = 4000 {\ mbox { фунтов на квадратный дюйм}}}
- n=0,8{\displaystyle n=0,8}
Дополнительные данные о резервуаре:
| р R (псиа) | k ro /μ o B o (cp -l ) | |||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 4000 |
| найти литературу по Основы течения жидкости |
- Исходный контент на страницах данных
- Найдите книгу в магазине AAPG
Основы потока жидкости — AAPG Wiki
Расчеты потока жидкости в скважине в основном сосредоточены на двух аспектах потока жидкости: профиле давления вдоль пути потока и зависимости дебита от давления в ключевых точках интереса (узлах). ), как показано на рисунке 1. Основные интересующие параметры (все в единицах фунтов на квадратный дюйм)
- p R = пластовое давление
- p wf = скважинное (забойное) гидродинамическое давление
- p wh = устьевое давление
- p sp = давление сепаратора
- p ST = давление в баке
Соответствующие ставки
- q o = дебит нефти (стб/сутки)
- q g = дебит газа (стандартные кубические футы/день)
Разность давлений ( p R – p wf ) называется депрессией пласта
7 .
 Это основная сила, направляющая пластовые флюиды в ствол скважины. Как правило, производительность увеличивается с увеличением просадки. Приток в ствол скважины, вызванный депрессией, называется притоком .
Это основная сила, направляющая пластовые флюиды в ствол скважины. Как правило, производительность увеличивается с увеличением просадки. Приток в ствол скважины, вызванный депрессией, называется притоком .
Взаимосвязь между расходом продукции, измеренным в резервуаре-накопителе, q o , а забойное гидродинамическое давление, p wf , называется зависимостью производительности притока (1PR) . IPR скважины можно определить непосредственно по данным эксплуатационных испытаний или его можно спрогнозировать по данным коллектора. Независимо от того, представлено ли оно графически или выражено формулой, IPR представляет собой отчет о производительности и широко используется для проектирования и анализа производительности скважин.
Хорошие общие ссылки на поток в пластах и скважинах включают Golan и Whitson, [1] Bradley, [2] и Craft et al. [3]
Содержание
- 1 Эмпирические уравнения IPR
- 1.
 1 Уравнение индекса продуктивности для недонасыщенной нефти
1 Уравнение индекса продуктивности для недонасыщенной нефти - 1.2 Уравнения противодавления для насыщенных нефтью и газом скважин
- 1.3 Квадратное уравнение для насыщенных нефтяных и газовых скважин
- 1.4 Ненасыщенное масло с расширенным диапазоном IPR
- 1.
- 2 Расширение закона Дарси
- 3 Радиальный поток
- 3.1 Единицы формулы закона Дарси
- 3.2 Ограниченный вход в ствол скважины (скин-эффект)
- 4 Зависимость теоретического давления от скорости (IPR)
- 4.1 Радиус дренажа
- 4.2 Расширение модели идеальной скважины
- 5 IPR, полученный в результате моделирования коллектора
- 6 Влияние истощения на формулы ПИС
- 7 Влияние стимуляции и повреждения на уравнения IPR
- 8 См. также
- 9Ссылки
- 10 Внешние ссылки
Эмпирические уравнения IPR
Рисунок 2 Графики многоступенчатых производственных данных.
Было разработано несколько формул IPR для представления поведения притока различных типов скважин. Сопоставление формулы с данными многодебитной добычи (рис. 2) позволяет определить значение характеристических констант в уравнениях, которые, в свою очередь, характеризуют продуктивность скважины. Эмпирические формулы являются основными инструментами для количественной оценки продуктивности скважин и выполнения расчетов добычи.
Уравнение индекса продуктивности для недонасыщенной нефти Уравнение
- qo = J (pR − pwf) {\ displaystyle q _ {\ rm {o}} = J (p _ {\ rm {R}} -p _ {\ rm {wf}})}
Постоянная характеристики связь дебита нефти с депрессией называется индексом продуктивности f и определяется как
- J = qopR−pwf {\ displaystyle J = {\ frac {q _ {\ rm {o}}} {p _ {\ rm {R}} -p _ {\ rm {wf}}}}}
с единицами STB/day/psi. Индекс продуктивности показывает количество баррелей в день, добытое на каждый фунт на квадратный дюйм снижения давления, и, таким образом, отражает производительность или пропускную способность скважины.
Когда p wf равно атмосферному давлению, скорость называется абсолютным открытым потоком (AOF) и часто обозначается как q max . AOF является полезным индикатором продуктивности скважины.
Уравнения противодавления для насыщенных нефтяных и газовых скважин[править] 9{n}}
Имеет две характеристические константы: константу противодавления c и показатель степени противодавления n . Показатель степени n представляет собой безразмерное число от 0,5 до 1,0. Он приближается к 1,0 для скважин с низким дебитом и к 0,5 для скважин с очень высоким дебитом. Значения n и c могут быть определены графически из логарифмического графика данных испытаний с несколькими скоростями в виде{2})}{q}}\quad {\mbox{versus}}\quad (A+Bq)}
Ненасыщенная нефть с расширенным диапазоном IPR b
при пластовом давлении выше точки насыщения ( p wf b p
R ), ПИС принимает форму, показанную на рисунке 2d. Его можно представить следующими уравнениями:
Его можно представить следующими уравнениями:
- для pwf> pb, qo = J (pR−pwf) {\ displaystyle {\ mbox {for}} p _ {\ rm {wf}}> p _ {\ rm {b}}, \ quad q _ {\ rm {o}}=J(p_{\rm {R}}-p_{\rm {wf}})} 9{2})}
Расширение закона Дарси[править]
Закон Дарси, первоначально разработанный для потока воды, был расширен для описания течения углеводородных пластовых флюидов (сжимаемых и многофазных).
Для однофазного потока нефти пропорциональная константа, которая связывает скорость потока с перепадами давления в исходном законе Дарси, разбивается на два независимых фактора: проницаемость породы, k , и вязкость жидкости, μ. Для линейной системы потока, это дает
- q=(A/L)(k/μ)Δp{\displaystyle q=(A/L)(k/\mu)\Delta p}
Проницаемость – это свойство породы, которое отражает «легкость», с которой жидкость течет через него. Вязкость является свойством жидкости и отражает сопротивление жидкости течению.
Для многофазного потока присутствие второй фазы в пористой среде снижает кажущуюся проницаемость первой фазы (например, присутствие газа снижает кажущуюся проницаемость нефти). Присутствие каждой фазы в пористой среде количественно определяется насыщенность, S , которая представляет собой отношение объема флюида в данной пористой породе к объему пор породы:
Присутствие каждой фазы в пористой среде количественно определяется насыщенность, S , которая представляет собой отношение объема флюида в данной пористой породе к объему пор породы:
- So = Vo / VpandSg = Vg / Vp {\ displaystyle S _ {\ rm {o}} = V _ {\ rm {o}} / V _ {\ rm {p}} \ quad {\ mbox {and}} \quad S _ {\ rm {g}} = V _ {\ rm {g}}/V _ {\ rm {p}}}
, где
- S o = нефтенасыщенность (доля)
- S г = газонасыщенность (доля)
- V o = объем нефти в данном объеме пор
- В г = объем газа в данном поровом объеме
- V p = объем пор
Рисунок 3 Двухфазная относительная проницаемость.
Кажущаяся или эффективная нефтепроницаемость k eo одной фазы в присутствии второй фазы может быть представлена как произведение двух членов: абсолютной проницаемости, k a , и относительной нефтепроницаемости, к ро :
- keo = ka × kro {\ displaystyle k _ {\ rm {eo}} = k _ {\ rm {a}} \ times k _ {\ rm {ro}}}
Абсолютная проницаемость является свойством породы и, по существу, представляет собой проницаемость, измеренную с одной фазой или при 100% однофазном насыщении. Относительная проницаемость представляет собой безразмерную величину, величина которой находится в диапазоне от 1,0 до 0, в зависимости от насыщенности (рис. 3). Относительные проницаемости измеряются в керновых (петрофизических) лабораториях, и результаты представляются в зависимости от насыщения. Некоторые лаборатории нормализуют значения относительной проницаемости со значениями, отличными от значений однофазного или 100%-ного насыщения, поэтому при интерпретации и использовании представленных данных необходимо соблюдать осторожность.
Относительная проницаемость представляет собой безразмерную величину, величина которой находится в диапазоне от 1,0 до 0, в зависимости от насыщенности (рис. 3). Относительные проницаемости измеряются в керновых (петрофизических) лабораториях, и результаты представляются в зависимости от насыщения. Некоторые лаборатории нормализуют значения относительной проницаемости со значениями, отличными от значений однофазного или 100%-ного насыщения, поэтому при интерпретации и использовании представленных данных необходимо соблюдать осторожность.
Радиальный поток[править]
Рисунок 4 Распределение давления в радиальном резервуаре.
Закон Дарси можно применить к идеальной модели скважины, обеспечивающей постоянный установившийся дебит. Модель предполагает цилиндрический поток в коллекторе, где поток через формацию является горизонтальным, а жидкость движется радиально по направлению к стволу скважины. Он также предполагает постоянную толщину продуктивной зоны, постоянную изотропную проницаемость и идеальную жидкость (однородную несжимаемую жидкость, в которой вязкость не зависит от давления).
Для резервуаров бесконечного размера результатом будет
- p = pwf + qμB2πkhln (r / rw) {\ displaystyle p = p _ {\ rm {wf}} + {\ frac {q \ mu B} {2 \ pi kh}} \ ln (r / r_ {\rm {w}})}
или в полевых единицах,
- p = pwf + 141,2qoμoBokhln (r / rw) {\ displaystyle p = p _ {\ rm {wf}} + {\ frac {141,2q _ {\ rm {o}} \ mu _ {\ rm {o }}B_{\rm {o}}}{kh}}\ln(r/r_{\rm {w}})}
То есть каждому радиусу r соответствует давление p логарифмически возрастает с р (рис. 4).
Распределение давления в радиально ограниченных резервуарах аналогично бесконечному случаю для большей части дренируемого объема. Однако вблизи границ, как показано на рисунке 4, все по-другому.
Единицы формулы закона Дарси Это гибридная система, состоящая из различных метрических, английских и нефтепромысловых единиц. Он использует миллидарси (md) для проницаемости. Другие размеры и единицы в этой системе следующие:
- q o = расход нефти в резервуаре (STB/день или баррелей в резервуаре в день)
- q г = расход газа (стандартные кубические футы в сутки или стандартные кубические футы в сутки)
- μ o = вязкость (сП или сантипуаз)
- B o = объемный коэффициент пласта (баррели RES/STB, или баррели резервуара к баррелям складского резервуара)
- p R = пластовое давление (psi)
- p wf = забойное давление (psi)
- k = проницаемость (мД)
- h = толщина продуктивного пласта (футы)
- r w = радиус ствола скважины (футы)
- r e = радиус дренажа (футы)
Формулы в следующем разделе даны в практических полевых единицах.
Ограниченный вход в ствол скважины (скин-эффект)[править]
Рисунок 5 Скин-эффект.
Фактическое распределение давления в большинстве случаев отличается от идеального распределения давления, полученного для идеальной модели. Следующее дополнительное падение давления в стволе скважины возникает в результате околоскважинных явлений (Рисунок 5):
- Δpskin = pwf (идеальный) − pwf (фактический) {\ displaystyle \ Delta p _ {\ rm {skin}} = p _ {\ rm {wf (идеальный)}} -p _ {\ rm {wf (фактический)} }}
Наиболее важными явлениями обычно являются конвергенция потока из-за ограниченного проникновения в продуктивную зону (частичное проникновение), нарушение проницаемости вблизи ствола скважины (повреждение пласта) и ограничение потока в перфорационных отверстиях.
Удобно выразить Δ p кожи в виде безразмерной величины s , называемой скин-фактором, который линейно пропорционален Δ p кожи :
- Δpskin = 141,2qoμoBokhs {\ displaystyle \ Delta p _ {\ rm {skin}} = {\ frac {141,2q _ {\ rm {o}} \ mu _ {\ rm {o}} B _ {\ rm {o }}}{kh}}s}
Скин-фактор может быть определен из интерпретации ГДИС и может быть легко преобразован в фактический Δ p скин или P wf(actual)*
Теоретическая зависимость давление-дебит (IPR)[править]
Закон Дарси, примененный к модели идеальной скважины, дает уравнение IPR, выраженное в терминах параметров резервуара. {0,5}}
{0,5}}
, где A — площадь дренирования скважины в квадратных футах, а радиус — в футах. Если площадь дренажа указана в акрах, ее необходимо преобразовать в квадратные футы, используя соотношение 1 акр = 43 560 футов 2 .
Расширение модели идеальной скважины[править]
Теоретически полученные уравнения IPR могут быть расширены для включения добычи газа и насыщенной нефти. Для газовых резервуаров низкого давления (менее 2000 фунтов на квадратный дюйм) используется следующее уравнение:
9{2})}{T\mu _{\rm {g}}Z[\ln(r _{\rm {e}}/r _{\rm {w}})-0,75+s]}}}
где
- q g = расход газа (стандартные кубические футы/день)
- T = температура (R° = F° + 460)
- Z = коэффициент сжимаемости газа
- μ г = вязкость газа (сП)
Все остальные параметры имеют те же единицы измерения, что и уравнения потока нефти. Существуют строгие методы, используемые для выражения IPR газовых скважин при пластовом давлении выше 2000 фунтов на квадратный дюйм. Однако уравнение низкого давления подходит для большинства расчетов производительности скважины.
Однако уравнение низкого давления подходит для большинства расчетов производительности скважины.
9{2})}
где срок к ро /мк o Б o оценивается при среднем пластовом давлении, р
и насыщенности.
При использовании этих уравнений следует помнить о двух практических соображениях. Во-первых, в зависимости от размещения скважин значение ln ( r e / r w ) находится в диапазоне от 6,5 до 8. Значение 7 является хорошим приближением для большинства расчетов производительности. Во-вторых, скин-фактор s положителен, когда вход в ствол скважины ограничен скин-эффектом. Отрицательно, если продуктивность лучше, чем предсказывает идеальная радиальная модель (например, в скважинах с стимуляцией или ГРП).
IPR, полученный на основе моделирования коллектора пластовых параметров. Формула, приведенная в нормализованном виде, имеет вид
- qoqmax = 1−0,2 (pwfpR) −0,8 (pwfpR) 2 {\ displaystyle {\ frac {q _ {\ rm {o}}} {q _ {\ rm {max}}}} = 1-0,2 \ left ({\ frac {p _ {\ rm {wf}}} {p _ {\ rm {R}}}} \ right) -0,8 \ left ({\ frac {p _ {\ rm {wf}}} {p _ {\ пм {R}}}}\вправо)^{2}}
Эта формула полезна для низкодебитных нефтяных скважин. Он завышает продуктивность высокодебитных скважин (производящих более 2000 баррелей в сутки).
Он завышает продуктивность высокодебитных скважин (производящих более 2000 баррелей в сутки).
Пример:
Скважина в резервуаре с растворенным газом имеет пластовое давление 4000 фунтов на квадратный дюйм. Одна контрольная точка равна q o = 200 STB/день с p wf = 3220 фунтов/кв. Подстановка данных в уравнение IPR и решение для q max дает
9{2}}}=624{\mbox{ STP/день}}}
Подстановка рассчитанного q max и заданного p R в уравнение вычисляет баллы по IPR следующим образом:
| pwf (псиа) | qo (STB/день) |
|---|---|
| 4000 | 0 |
| 3000 | 250 |
| 2000 | 437 |
| 1500 | 508 |
| 1000 | 562 |
Влияние истощения на формулы ПИС
Истощение обычно приводит к ухудшению IPR (рис. 6). Эти изменения можно предсказать количественно, рассчитав изменения характеристических констант: j , c , q ax A и B . Показатель степени n не меняется при истощении. Если индекс p обозначает текущее состояние истощения, а нижний индекс f — будущее состояние, настоящий и будущий характерные факторы связаны следующим образом:
6). Эти изменения можно предсказать количественно, рассчитав изменения характеристических констант: j , c , q ax A и B . Показатель степени n не меняется при истощении. Если индекс p обозначает текущее состояние истощения, а нижний индекс f — будущее состояние, настоящий и будущий характерные факторы связаны следующим образом:
Для резервуаров с недонасыщенной нефтью:
- JfJp = (μoBo) p (μoBo) f {\ displaystyle {\ frac {J _ {\ rm {f}}} {J _ {\ rm {p}}}} = {\ frac {(\ mu _ { \ rm {o}} B _ {\ rm {o}}) _ {\ rm {p}}} {(\ mu _ {\ rm {o}} B _ {\ rm {o}}) _ {\ rm { f}}}}}
Газовые резервуары низкого давления:
- cf = cpandnf = np {\ displaystyle c _ {\ rm {f}} = c _ {\ rm {p}} \ quad {\ mbox {and}} \ quad n _ {\ rm {f}} = n_ { \гт {р}}} 9{n}}
, где
- qo max=480 STB/день{\displaystyle q_{\rm {o\ max}}=480{\mbox{STB/день}}}
- pR = 4000 фунтов на квадратный дюйм {\ displaystyle p _ {\ rm {R}} = 4000 {\ mbox { фунтов на квадратный дюйм}}}
- n=0,8{\displaystyle n=0,8}
Дополнительные данные о резервуаре:
| р R (псиа) | k ro /μ o B o (cp -l ) |
|---|---|
| 4000 |



 1 Уравнение индекса продуктивности для недонасыщенной нефти
1 Уравнение индекса продуктивности для недонасыщенной нефти 8}}
8}} : Englewood Cliffs, NJ, Prentice Hall.
: Englewood Cliffs, NJ, Prentice Hall. 1 Уравнение индекса продуктивности для недонасыщенной нефти
1 Уравнение индекса продуктивности для недонасыщенной нефти