Как высчитать площадь треугольника крыши: Как рассчитать площадь крыши — скатной кровли, квадратуру крыши. Пример расчета площади кровли

Как рассчитать площадь крыши. Подсчет площади крыши

Грамотный расчет площади крыши дома – разумный подход к покупке кровельного покрытия, теплоизоляции и других строительных материалов. Уметь это нужно и для того, чтобы она не рухнула под собственным весом или под тяжестью осадков. Понимание, как и откуда берутся цифры подсчетов поможет вам составить смету, проконтролировать рабочих, экономно рассчитать свои средства, а если не вписываетесь в них — внести поправки в чертежи.

Общие рекомендации

Когда система стропил уже возведена, но проект здания отсутствует, над планом крыши работают отдельно. Вооружившись углом и рулеткой, обмеряем здание и наносим чертеж на бумагу. Промеряем все высоты от коньков до перекрытий (в случае нескольких уровней) и вносим их в чертеж. Перед тем как начать считать площадь крыши, для наглядности попробуйте отобразить вашу кровлю в проекции.

Уделите внимание свесам и укажите на чертеже их размеры и местоположение. Проще всего делать расчет площади крыш, у которых на скатах отсутствуют изломы. Важно помнить:

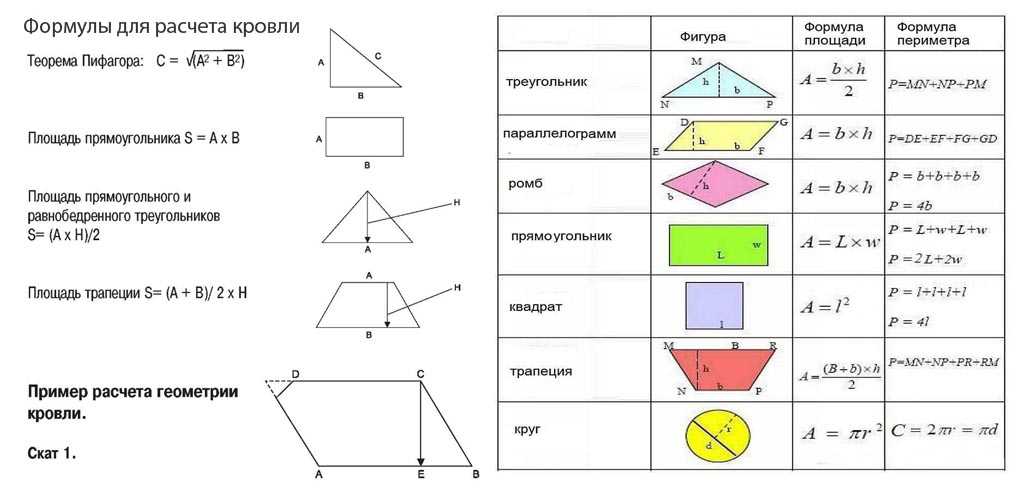
1. Форму крыши лучше разложить на правильные геометрические фигуры – треугольники, квадраты, трапеции, ромбы.
2. Если у вас на руках план со схемой, то считайте площадь по нему, а затем умножьте результат на косинус угла наклона.
3. К полученному значению приплюсуйте еще около 10%, это покроет погрешности и разные непредвиденные ситуации.
4. Как правило, новички норовят высчитать из площади крыши дымоходные трубы, мансардные окна, люки, вентиляционные отверстия и другие конструкции. Этого категорически нельзя делать: видимая экономия грозит нехваткой материала.
5. Наличие точного плана заметно ускоряет и упрощает процесс вычислений.
6. Для определения подъема конька, в зависимости от угла уклона, используется поправочный коэффициент:

• 7° – 0,124;
• 8° – 0,143;
• 10° – 0,181;
• 13° – 0,238;
• 15° – 0,269;
• 18° – 0,325;
• 22° – 0,408;
• 30° – 0,574;
• 35° – 0,704;
• 40° – 0,839.

Особенности расчета для различных видов крыш

Плоская крыша. Ее еще называют инверсионной и чаще всего используют для хозяйственных построек. Подсчет не представляет сложности. Из начального курса геометрии помним: длина умножается на ширину.

Односкатная крыша. Как правило, вычислить ее площадь также легко, как у для плоской крыши, учитываем лишь выступы со всех четырех сторон.

Двускатная. Наиболее популярный вариант при строительстве среднегабаритных частных домов. Определение площади крыши такого типа не занимает много времени.

1. Если обе половины одинаковы, то все просто: считаем площадь одного прямоугольника и умножаем вдвое.
2. Длина ската считается так: длина стены, вдоль которой он расположен + выступ над фронтоном, умноженный на 2. Ширина – это длина стропила + 1 выступ над стеной. Например, если скат 10 м, а коньковая часть 6 м, то общая площадь крыши равняется: 2(10х6)=120 м².
3. Для расчета высоты крыши берем ½ ее ширины и умножаем на коэффициент угла уклона. Например, ширина дома 10 м с уклоном кровли 30°. 5х0,574=2,87. Значит, высота конька будет равняться 2,87 м.
4. Узнать размер верхнего стропила можно еще и по формуле. Половинную длину горизонтальной балки фронтона делим на косинус прилегающего угла.
5. Если у вас дом со скатами прямоугольной формы, а перед глазами лишь ее вид сверху, то как посчитать площадь крыши дома? Для этих целей есть несложная формула: S=(2a+b)x(2a+c)х cos40, где a – ширина свеса, b – длина дома, c – ширина дома, 40 – угол наклона крыши. Итак, если у нас дом 12 м длиной, 8 м шириной, свесы по 0,5 м, а косинус угла 40 равен 0,77, то S=(2х0,5+12)х(2х0,5+8)х0,77=90,1 м².

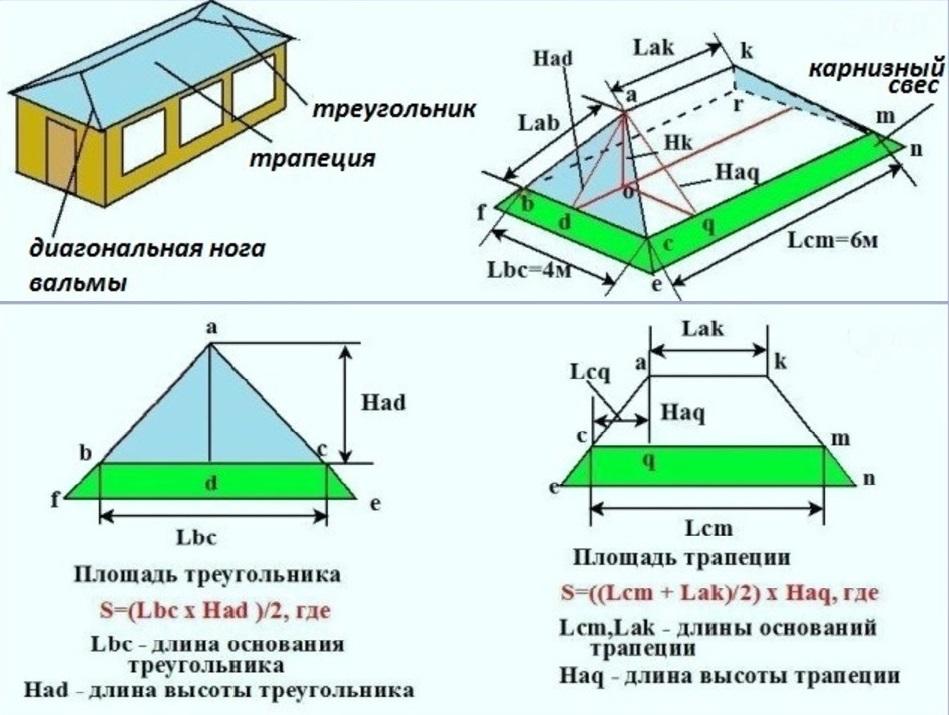
Четырехскатная крыша бывает вальмовая и шатровая. У обеих все скаты расположены под углом к основанию, но если у первого типа на вершине образуется ребро, то у второго все плоскости сходятся в одну точку. Как правильно рассчитать площадь подобной крыши? Сперва разбиваем ее поверхность на простые фигуры.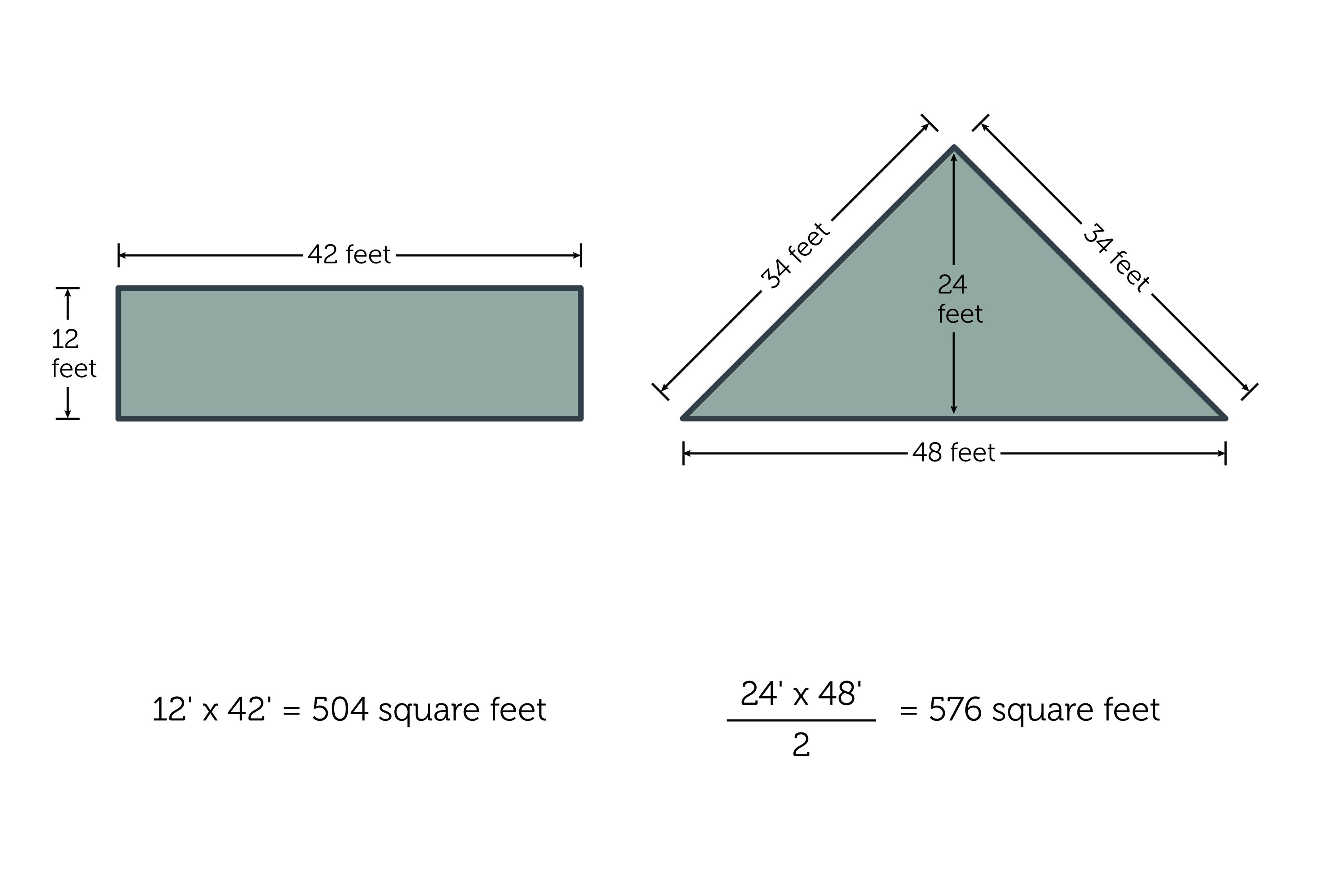 У вальмовой получаем 2 треугольника и 2 трапеции; шатровая состоит из 4 треугольников.

Рассчитываем площадь крыши дома по школьным формулам. Для треугольников: S=(bxh)/2, где b – длина основания фигуры, а h – высота треугольника. Для трапеции: S=((a+b)/2)xh, где a, b – основания.

Поскольку шатровая форма иначе называется пирамида, то из курса геометрии вспоминаем, что площадь ее боковой поверхности равна сумме длин ее боковых граней. Это облегчит нам подсчет погонного метража коньков, уголков и так далее.

Полувальмовая, многощипцовая крыша. Если имеется конструкция из прямоугольников, выходящих друг из друга и пересекающихся, то перед нами многощипцовая форма. Процесс расчетов аналогичен, но, возможно, займет больше времени. В каждом внутреннем стыке находится ендова, не забудьте и про ее погонаж.

Как найти площадь крыши для укладки кровельного покрытия?

Полученные данные могут оказаться вдвое больше посчитанной до этого площади. Объясняется всё тем, что у листов для скатов неправильной формы срезают углы и подгоняют под размер. Чем сложнее ваша конструкция, тем больше будет обрезков.

Шифер, профнастил, металлочерепица. Данные покрытия выпускаются в листовой форме и кладутся с нахлестом. Есть такое понятие, как полезная площадь единицы материала, поэтому при расчетах нужно отталкиваться не от номинальной ширины, а от полезной. Добросовестный производитель всегда указывает эти параметры на своем продукте. Для правильного рассчета полезно будет знать схему укладки кровельного покрытия.

Длина листа металлочерепицы колеблется от 50 до 650 см, а профнастила – от 50 до 1200 см. Не стоит брать листы наибольшей длины для экономии на стыках: такая транспортировка перекроет вашу экономию, а количество отходов увеличится. Итак, три шага, как узнать площадь настила крыши.

1. Длину строения делим на ширину листа и к полученной цифре добавляем 10%, а то и 15% на прирезку. Так нам становится известно, сколько листов нужно для одного ряда.
2. Берем длину ската от конька до карниза и делим на длину шиферного листа. К результату прибавляем 13% — это нахлест при монтаже, который для металлочерепицы и профнастила составляет примерно 10 см.
3. Количество рядов умножаем на количество листов для одного ряда и получаем требуемый расход. Не забудьте также подсчитать количество погонных метров материала для коньков, ендов и парапетов. Как видно, рассчитать площадь крыши – не так уж сложно.

Цементно-песчаный и гибкий настил. Мягкие рулонные материалы – наиболее популярный вид покрытия четырехскатных крыш. Как правило, на упаковках с этим материалом производитель указывает его полезную площадь и прирезка уже включена. Общий процент наслоения равняется примерно 10 и высчитывается аналогично шиферу.

Как посчитать площадь утеплителя для крыши дома? Это несложно, необходимо умножить площадь скатов на толщину слоя материала. На упаковках с утеплителем всегда указывается его количество внутри и вы сможете сами прикинуть, сколько вам потребуется.

Чем точнее будут расчеты, тем меньше вам придется переплачивать за материалы. Если форма несколько сложна, и вы сомневаетесь в том, как правильно определить площадь крыши и не ошибиться в своих подсчетах, интернет вам в помощь: есть специальные строительные онлайн калькуляторы, которые предназначены для этих целей. Вы также можете освоить простенькую программу, которая выдаст вам все инструкции по кровле, исходя из заданных параметров. То, каким образом вы решили рассчитать площадь крыши, не должно влиять на результат. Используйте несколько способов, чтобы перепроверить себя.

Тонкости стройки: как посчитать площадь фронтона

Вопрос о том, как посчитать площадь фронтона, возникает часто. Фронтон является одним из важнейших элементов конструкции крыши. Он оказывает существенное влияние на дизайн дома и на ландшафтный дизайн приусадебного участка.

Фронтон оказывает большое влияние на ландшафтный дизайн участка и дизайн самого дома.

При этом важно не только правильно сделать расчет его площади, но и тщательно подобрать материалы для его обшивки.

Стоит отметить, что фронтоны для двухскатной крыши имеют значительно большую площадь, чем на четырехскатных (не шатровых). Многие фирмы, которые изготавливают, или магазины, которые продают материалы для обшивки, предоставляют услуги по расчету площади. Однако стоят такие услуги недешево. Поэтому выполнить расчет площади можно самому, тем более что сделать это достаточно просто. О том, как быстро и просто посчитать площадь фронтона дома, будет рассказано ниже.

Содержание

1. Что такое фронтон?
2. Что нужно знать перед началом расчетов?
3. Проведение расчетов: два варианта
4. Некоторые советы

Что такое фронтон?

Схема фронтона с сайдинговой отделкой.

Фронтоном называют торцевую часть крыши, которая имеет вид треугольника и образуется у той стены, где стыкуются скаты. В этой точке стропильная система опирается на карниз.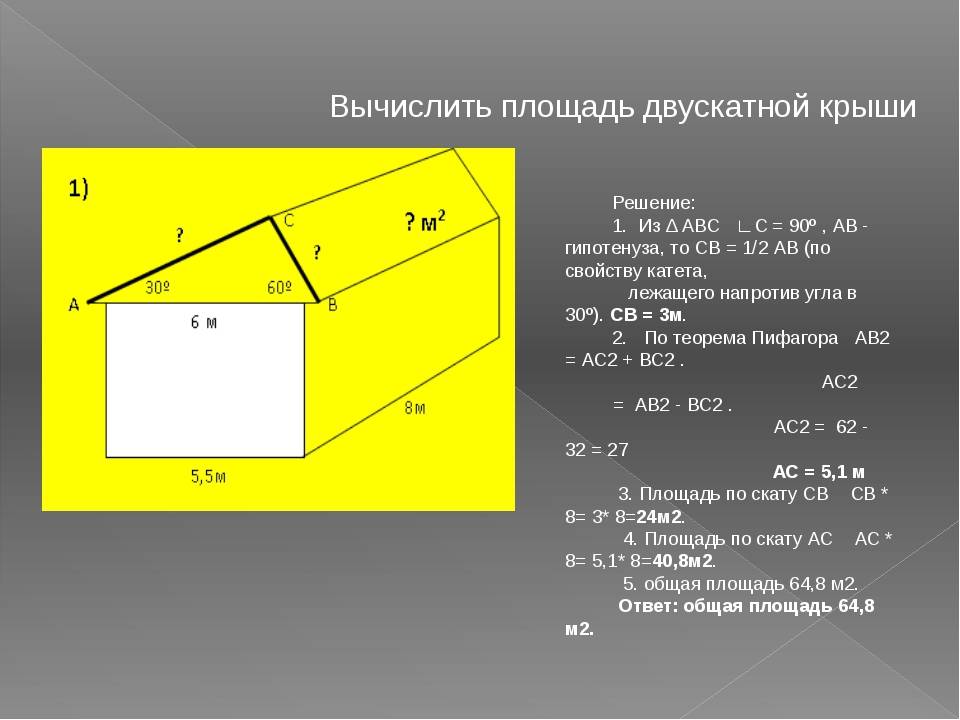 Поэтому основная задача фронтона — обеспечение достаточно надежной опоры для стропил. А вот фронтонной называют стену, над которой он находится, без учета самого фронтона.

Пространство фронтона, которое следует зашивать, находится между скатами крыши. Чаще всего фронтон имеет форму треугольника, реже — трапеции, иногда можно встретить портики экзотических форм. Это связано с тем, что форма напрямую зависит от типа конструкции стропильной системы. Фронтоны очень часто делают в средней полосе России, на домах, где есть ломаная крыша или обычная двускатная. Фронтон крыши имеет ряд недостатков, например, крыши с портиками нельзя строить в регионах, где частые ураганы, сильные ветра и т.д. Однако несмотря на недостаток, фронтон очень практичен: обшитый портик предохраняет перекрытия и стропильную систему от попадания влаги и существенно экономит ресурсы при строительстве крыши (для него не требуется выбранное кровельное покрытие). При строительстве важно учесть и его свес: он может быть любым и под любым наклоном. Из-за наклона площадь может увеличиваться, есть необходимость в тщательном подборе материалов для обшивки. Важно учитывать все эти факторы, поэтому рекомендуется для расчета пригласить профессиональных строителей.

Рассчитать площадь фронтона при проектировании кровли необходимо очень тщательно, поскольку в случае допущения ошибок возможны перекосы стропил, что приведет к негерметичности крыши. Поэтому перед началом строительства необходимо вычислить площадь.

Вернуться к оглавлению

Что нужно знать перед началом расчетов?

Самое важное значение для расчета площади фронтона имеет высота кровли. От нее зависит и высота портика. Поэтому перед проведением расчетов площади необходимо знать это значение. При этом для односкатных крыш он выкладывается сразу при строительстве стены. Шатровые крыши фронтонов не имеют. Поэтому в примере будут рассмотрены односкатные и двускатные крыши. При этом сложность конструкции не имеет никакого значения: сложные виды можно условно разделить на простые геометрические фигуры (трапеции, прямоугольники, треугольники).

После определения высоты крыши необходимо узнать углы наклона скатов. Стандартно эти углы находятся в диапазоне от 14 до 45° (кроме плоских крыш: они не имеют углов наклона и фронтонов).

Прежде, чем проводить расчет высоты крыши, нужно определиться с ее типом.

Чаще всего крыши строят в промежутке от 30 до 45°. Это зависит от дизайна дома, региона и личных предпочтений хозяина. Замеры углов производят специальными угломерами. Угол наклона скатов можно узнать из проекта дома, там его обязаны указать. Однако это не отменяет проведение замеров на месте, поскольку при строительстве могли быть допущены ошибки или изменения, которые не внесли в проект.

Последним важным моментом перед началом расчета конструкции является определение материала для обшивки. В основном материал подбирают по личным предпочтениям/вкусам и толщине кошелька, но в некоторых случаях необходимо использовать строго оговоренные в проекте материалы. Например, в случае когда фронтон является естественным продолжением стены, его лучше сделать из того же материала, что и стену. Высота крыши (и, соответственно, фронтона) является определяющей для высоты чердака. При высокой крыше на чердаке возможно оборудовать комнату или мансарду, соответственно, это наложит ограничения на материалы и сделает необходимым установку одного или нескольких окон в нем. При этом материалы должны быть крепкими, а конструкция должна обеспечивать высокую прочность, поскольку на фронтон будет приходиться часть нагрузки от стропильной системы. Поэтому при обшивке их деревом, панелями и т.д. необходимо заранее сделать мощный каркас, который сможет выдержать и стропила, и обшивку. Одним из вариантов будет выкладывание из кирпича или газобетона высокой плотности.

Стоит учесть и то, что фронтон может выступать над стенами дома. Для его усиления необходимо применять металлические или ж/б детали (иногда применяют и деревянный брус), которые обеспечат высокую прочность конструкции. При этом ограничений по материалам для обшивки нет.

Вернуться к оглавлению

Проведение расчетов: два варианта

Расчет площади фронтона методом параллелограмма.

Посчитать размеры фронтона достаточно просто. Для этого необходимы знания геометрии седьмого класса по вычислению площади фигур. Их измеряют в квадратных метрах. В данном случае рассмотрим два варианта подсчетов для фронтона трапециевидной формы и для треугольной формы:

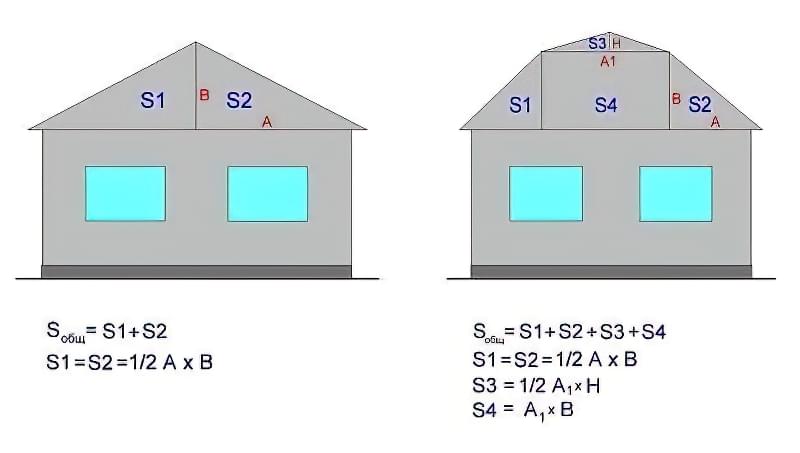
1. Самая простая форма — треугольная. Все помнят из школьного курса, что площадь треугольника равна половине произведения высоты на основание, к которому опущена высота: S = 0,5 h*l, где S — площадь, h — длина высоты, l — длина основания. В случае строительства под высотой будет пониматься высота крыши (от перекрытия до коньковой балки), а длина основания равна длине стены, над которой возводится фронтон. При этом не имеет значения то, что крыша может быть несимметричной: площадь треугольного вида от разных углов наклона не изменится (однако это повлияет на конструкцию каркаса и разделку материалов).
2. Трапециевидный считается просто. Его площадь равна произведению высоты на среднюю линию (длина средней линии есть половина суммы длин оснований) S = h * 0,5 (a+b), где S — площадь, a и b — длины оснований (одно основание — стена, второе — плоскость кровли).

При отсутствии значения высоты ее легко найти по теореме Пифагора или зная углы наклона скатов.

В случае если форма фронтона достаточно сложная, ее разбивают на прямоугольные треугольники и прямоугольники, затем считают площадь полученных фигур, а результаты складывают.

Примеры:

Расчет площади фронтона методом треугольника.

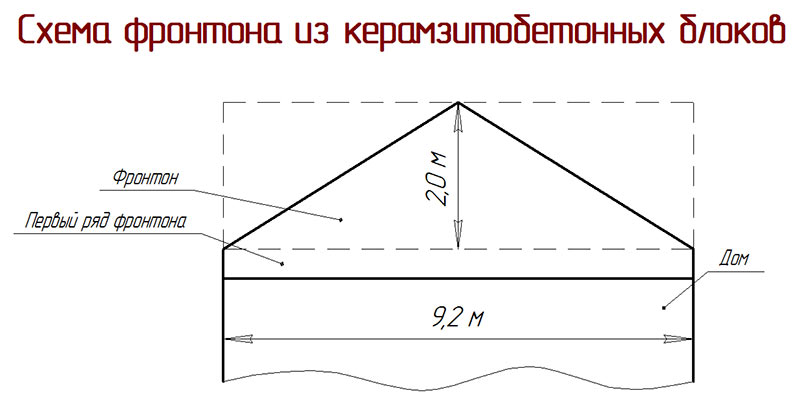
1. Дом с двускатной крышей (фронтон треугольной формы) с одинаковыми скатами. Ширина дома составляет 8 м, угол наклона ската 35° (его тангенс равен 0,71). Сначала следует рассчитать высоту крыши, она равна 0,5*8*0,71= 2,85 м. Соответственно, площадь такого фронтона равна 0,5*8*2,85= 11,4 м². Важно помнить, что в этом случае их будет 2.
2. Трапециевидный считается легко. Дано: длина стены 12 м, длина верхнего ребра крыши составляет 6 м, высота фронтона крыши составляет 4 м. Площадь при этом будет равна 4*0,5*(12+6) = 36 м².

При этом важно помнить, что фронтонов может быть несколько, поэтому необходимо рассчитать площади каждого и потом сложить (это нужно для определения количества строительных материалов).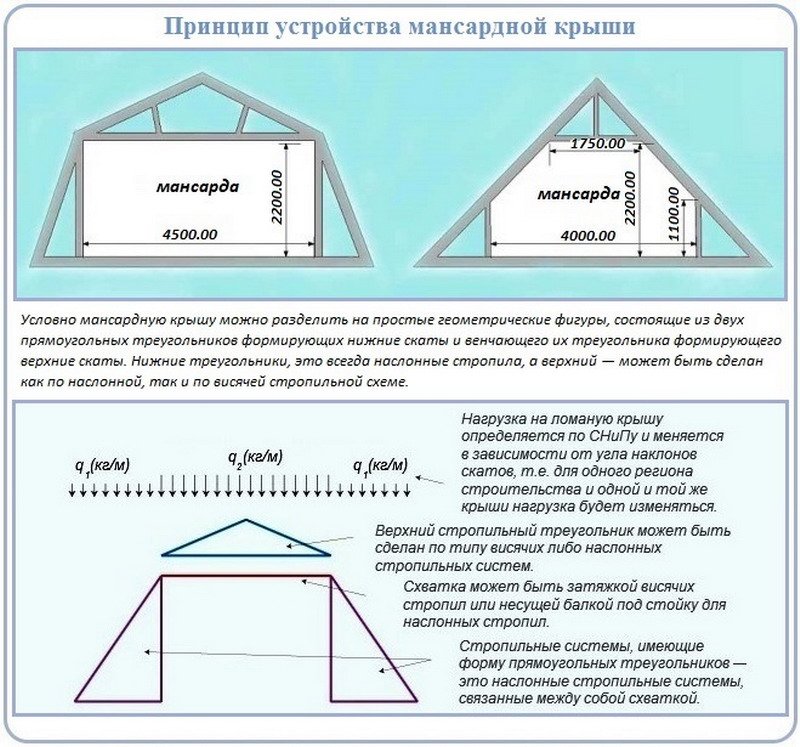 Стоит вычесть из площади фронтона площадь окон (это могут быть как полноценные мансардные окна, так и слуховые). Также при обивке их деревом необходимо учесть то, что щели надо будет конопатить мхом или другим материалом.

Вернуться к оглавлению

Некоторые советы

Перед началом строительства желательно сделать подробные чертежи. Это позволит более точно посчитать их площадь и определить расположение окна.

Разработку чертежей рекомендуется заказать в архитектурном ателье или строительном конструкторском бюро, это даст гарантию отсутствия ошибок и позволит избежать экспертиз БТИ при оформлении постройки.

Площадь треугольника — Как найти площадь треугольника | Формулы

Определение
Формулы площади треугольника
Площадь прямоугольного треугольника
Площадь равностороннего треугольника
Площадь равнобедренного треугольника
Периметр треугольника
Площадь треугольника по формуле Герона
Площадь треугольника — условие SAS
Примеры
Часто задаваемые вопросы

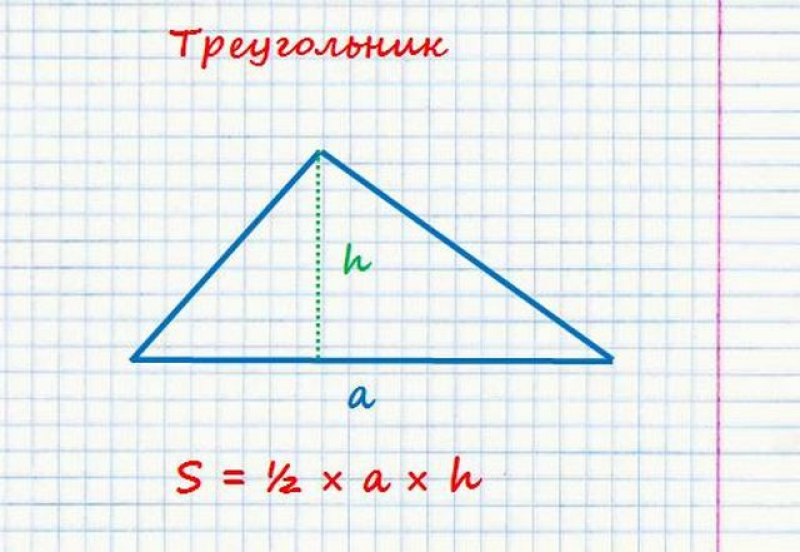
Площадь треугольника — это заключенная им область в двумерной плоскости.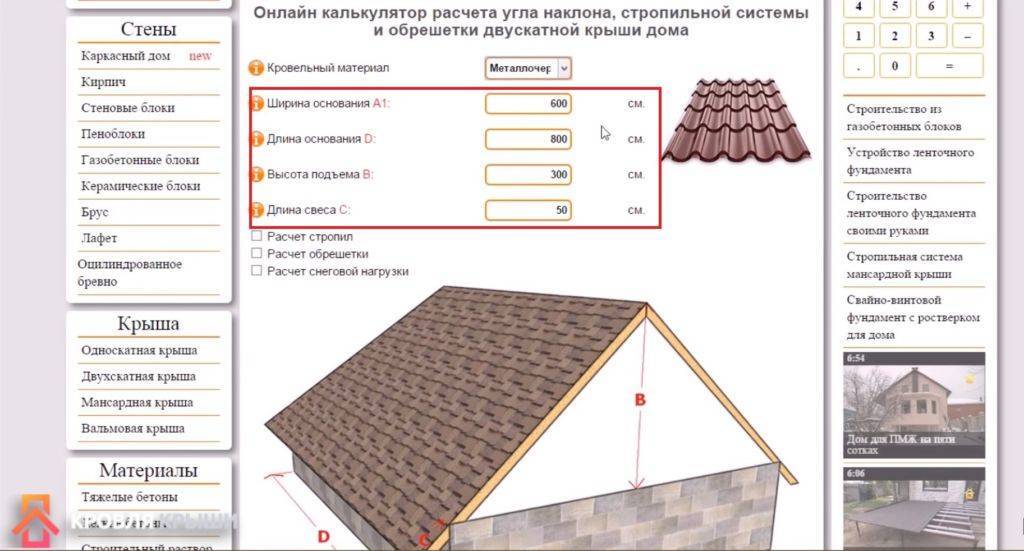 Как известно, треугольник — это замкнутая фигура, имеющая три стороны и три вершины. Таким образом, площадь треугольника — это общее пространство, занимаемое тремя сторонами треугольника. Общая формула для нахождения площади треугольника дается половиной произведения его основания и высоты.

В общем, термин «площадь» определяется как область, занимаемая внутри границы плоского объекта или фигуры. Измерение производится в квадратных единицах, стандартной единицей измерения являются квадратные метры (м ² ). Для вычисления площади существуют предопределенные формулы для квадратов, прямоугольников, кругов, треугольников и т. д. В этой статье мы изучим формулы площади треугольников для различных типов треугольников, а также рассмотрим некоторые примеры задач.

Какова площадь треугольника?

Площадь треугольника определяется как общая область, заключенная между тремя сторонами любого конкретного треугольника. По сути, он равен половине основания, умноженному на высоту, т. е. A = 1/2 × b × h. Следовательно, чтобы найти площадь трехстороннего многоугольника, мы должны знать его основание (b) и высоту (h) . Он применим ко всем типам треугольников, будь то разносторонний, равнобедренный или равносторонний. Следует отметить, что основание и высота треугольника перпендикулярны друг другу. Единица площади измеряется в квадратных единицах (м ² , см ² ).

Пример: Чему равна площадь треугольника с основанием b = 3 см и высотой h = 4 см?

Используя формулу,

Площадь треугольника, A = 1/2 × b × h

= 1/2 × 4 (см) × 3 (см)

= 2 (см) × 3 (см)

= 6 см ²

Помимо приведенной выше формулы, у нас есть формула Герона для вычисления площади треугольника, когда мы знаем длины его трех сторон. Также тригонометрические функции используются для нахождения площади, когда мы знаем две стороны и угол, образованный между ними в треугольнике. Рассчитаем площадь для всех приведенных здесь условий.

Площадь треугольника Формула

Площадь треугольника определяется по приведенной ниже формуле:

, где b и h — основание и высота треугольника соответственно.

Теперь давайте посмотрим, как вычислить площадь треугольника по данной формуле. Формулы площади для всех различных типов треугольников, таких как площадь равностороннего треугольника, прямоугольного треугольника, равнобедренного треугольника, а также способы нахождения площади треугольника с 3 сторонами с использованием формулы Герона с примерами приведены ниже.

Площадь прямоугольного треугольника

Прямоугольный треугольник, также называемый прямоугольным треугольником, имеет любой угол, равный 90°. Следовательно, высота треугольника будет равна длине перпендикулярной стороны.

Площадь прямоугольного треугольника = A = ½ × основание × высота (перпендикулярное расстояние)

Из приведенного выше рисунка

Площадь треугольника ACB = 1/2 × a × b

Площадь равностороннего треугольника

Равносторонний треугольник – это треугольник, у которого все стороны равны. Перпендикуляр, проведенный из вершины треугольника к основанию, делит основание на две равные части. Чтобы вычислить площадь равностороннего треугольника, нужно знать размеры его сторон. 9{2}}\конец{массив} \)

Читайте также:

Площадь треугольника с тремя сторонами (формула Герона)

Площадь треугольника с тремя сторонами разной величины можно вычислить по формуле Герона. Формула Герона включает два важных шага. Первый шаг — найти полупериметр треугольника, сложив все три стороны треугольника и разделив его на 2. Следующий шаг — применить значение полупериметра треугольника в основной формуле под названием «Формула Герона», чтобы найти площадь треугольника.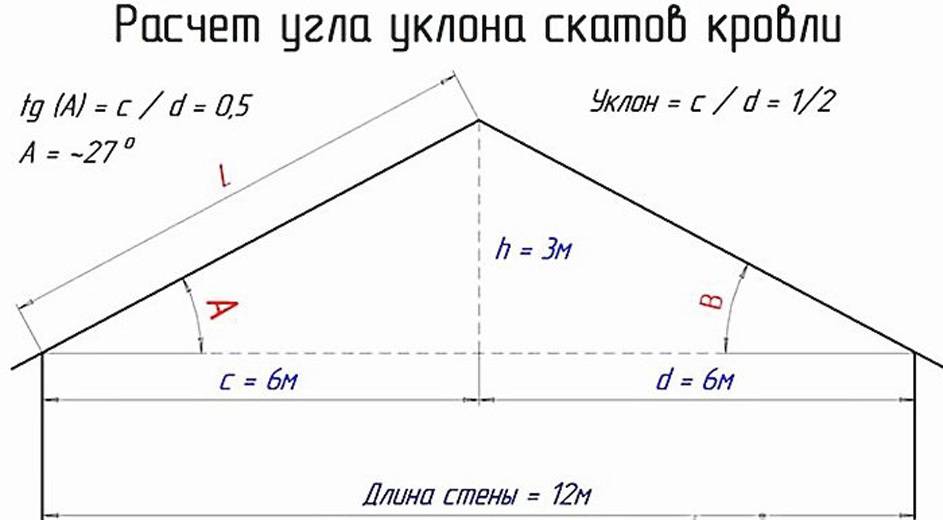

где s — полупериметр треугольника = s = (a+b+c) / 2

Мы видели, что площадь особых треугольников может быть получена с помощью формулы треугольника. Однако для треугольника с заданными сторонами вычисление высоты будет непростым. По той же причине мы полагаемся на формулу Герона для вычисления площади треугольников с неравными длинами.

Площадь треугольника по двум сторонам и прилежащему углу (SAS)

Теперь возникает вопрос, когда мы знаем две стороны треугольника и угол между ними, то как найти его площадь.

Возьмем треугольник ABC, углы при вершинах которого равны ∠A, ∠B и ∠C, а стороны равны a,b и c, как показано на рисунке ниже.

Теперь, если даны любые две стороны и угол между ними, то формулы для вычисления площади треугольника задаются следующим образом:

Площадь (∆ABC) = ½ до н.э. sin A

Площадь (∆ABC) = ½ абс. C

Площадь (∆ABC) = ½ корпуса B

Эти формулы очень легко запомнить, а также легко вычислить.

Например, если в ∆ABC A = 30° и b = 2, c = 4 в единицах. Тогда площадь будет;

Площадь (∆ABC) = ½ до н.э. sin A

= ½ (2) (4) sin 30

= 4 x ½   (поскольку sin 30 = ½)

= 2 кв.ед.

Связанные статьи

Примеры решения площади треугольника

Пример 1:

Найдите площадь остроугольного треугольника с основанием 13 дюймов и высотой 5 дюймов.

Решение:

A = (½)×b×h кв.ед.

⇒ А = (½) × (13 дюймов) × (5 дюймов)

⇒ A = (½) × (65 в ² )

⇒ A = 32,5 в ²

Пример 2:

Найдите площадь прямоугольного треугольника с основанием 7 см и высотой 8 см.

Решение:

A = (½) × b × h кв.ед.

⇒ А = (½) × (7 см) × (8 см)

⇒ А = (½) × (56 см ² )

⇒ А = 28 см ²

Пример 3:

Найдите площадь тупоугольного треугольника с основанием 4 см и высотой 7 см.

Решение:

A = (½) × b × h кв.ед.

⇒ А = (½) × (4 см) × (7 см)

⇒ А = (½) × (28 см ² )

⇒ А = 14 см ²

Часто задаваемые вопросы о площади треугольника

Q1

Какова площадь треугольника?

Площадь треугольника — это область, ограниченная его периметром или тремя сторонами треугольника.

Q2

Какова площадь, если даны две стороны треугольника и угол между ними?

Площадь будет равна половине произведения двух данных сторон и синуса прилежащего угла.

Q3

Как найти площадь треугольника по трем сторонам?

Когда известны значения трех сторон треугольника, мы можем найти площадь этого треугольника, используя формулу Герона. Обратитесь к разделу « Площадь треугольника по формуле Герона », упомянутому в этой статье, чтобы получить полное представление.

Q4

Как найти площадь треугольника с помощью векторов?

Предположим, что векторы u и v образуют треугольник в пространстве. Тогда площадь этого треугольника равна половине величины произведения этих двух векторов, так что

  A = ½ |u × v|

Q5

Как вычислить площадь треугольника?

Для данного треугольника, где основание треугольника равно b, а высота равна h, площадь треугольника может быть рассчитана по формуле, например;

A = ½ (b × h) Квадратный блок

Калькулятор площади треугольника

Создано Ханной Памула, доктором философии

Отредактировано Богной Шик и Аденой Бенн 093 Как использовать этот калькулятор площади треугольника?

Этот калькулятор площади треугольника может помочь в определении площади треугольника. В базовой формуле площади треугольника должны быть заданы основание и высота, но что, если у нас их нет? Как вычислить площадь треугольника, у которого только 3 стороны? Калькулятор площади треугольника здесь для вас. Попробуй! Если вы все еще не знаете, как найти площадь треугольника, посмотрите описание ниже.

Формула площади треугольника

Треугольник — одна из основных геометрических фигур. Самая известная и самая простая формула, которую почти все помнят со школы:

• площадь = 0,5 * b * h , где b — длина основания треугольника, а h — высота треугольника.

Однако иногда трудно найти высоту треугольника. В этом случае можно использовать многие другие уравнения, в зависимости от того, что вы знаете о треугольнике:

• Три стороны (SSS)

  Если известны длины всех сторон, используйте формулу Герона:

  площадь = 0,25 * √( (a + b + c) * (-a + b + c) * (a - b + c) * (a + b - c))

• Две стороны и угол между ними (SAS)

  Вы можете легко вычислить площадь треугольника с помощью тригонометрии:

  площадь = 0,5 * a * b * sin(γ)

• Два угла и сторона между ними (ASA)

  Существуют различные версии формул площади треугольника — для ее получения можно использовать, например, тригонометрию или закон синусов:

  площадь = a² * sin(β) * sin(γ) / (2 * sin(β + γ))

Если вы ищете другие формулы или калькуляторы, связанные с треугольниками, посмотрите этот калькулятор прямоугольного треугольника, калькулятор теоремы Пифагора и калькулятор закона косинусов.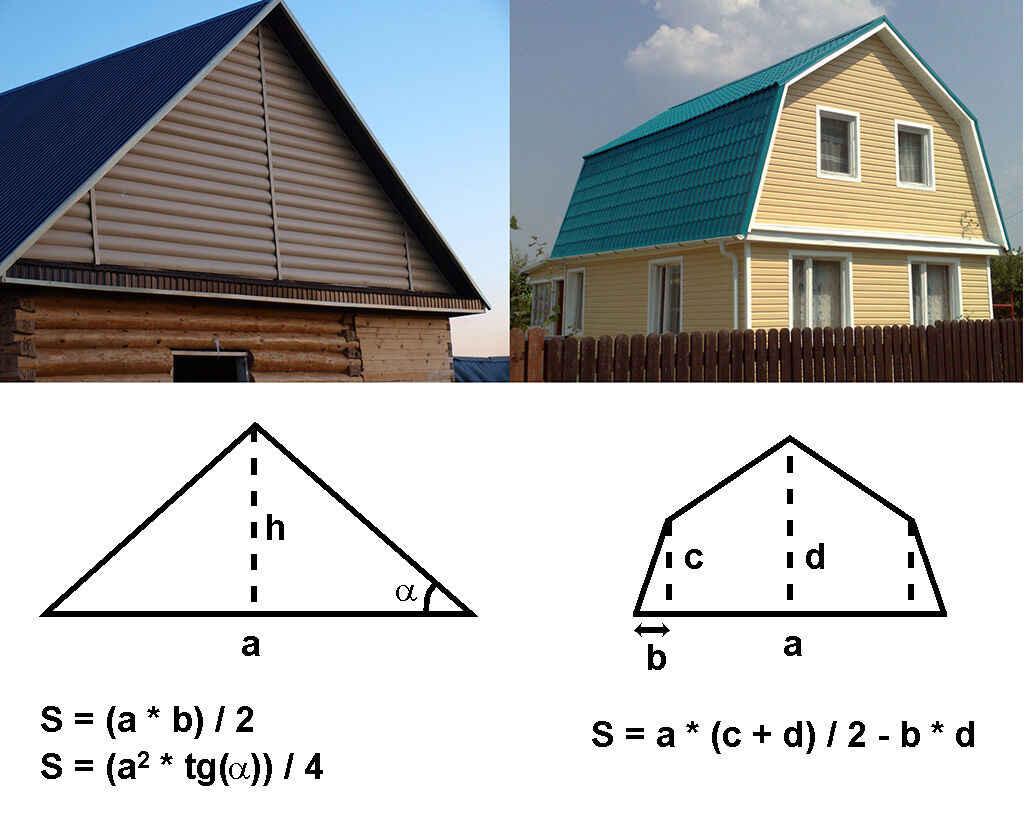

Как использовать этот калькулятор площади треугольника?

Предположим, что мы знаем две стороны и угол между ними:

1. Введите длину первой стороны . В нашем примере он может быть равен 9 дюймам

.

2. Введите вторую сторону треугольника . Давайте выберем 5 дюймов.
3. Определить угол между двумя известными сторонами . Например, 30 градусов.
4. Посмотрите, как наш калькулятор площади треугольника выполняет все расчеты за вас! Площадь для нашего случая равна 11,25 дюйма².

Как вычислить площадь равностороннего треугольника?

Чтобы вычислить площадь равностороннего треугольника, нужно знать только сторону:

площадь = a² × √3/4

мы можем сформулировать быстрый рецепт: аппроксимировать площадь равностороннего треугольника, возвести в квадрат длину стороны, а затем умножить на 0,433 .

Хотя мы подготовили отдельный калькулятор для площади равностороннего треугольника, вы можете быстро рассчитать ее в этом калькуляторе площади треугольника. Просто используйте подраздел для площади треугольника с 3 сторонами — как вы знаете, каждая сторона имеет одинаковую длину в равностороннем треугольнике. Эту площадь можно рассчитать и в угол-сторона-угол или сторона-угол-сторона версия — вы, наверное, помните, что каждый угол в равностороннем треугольнике равен 60 градусам (π/3 рад).

Часто задаваемые вопросы

Как найти площадь треугольника по сторонам?

Если известны длины всех сторон ( a , b и c ) треугольника, можно вычислить его площадь:

1. Вычислить половину периметра ½(а + b + с) . Обозначим это значение через с .
2. Вычислить s-a , s-b и s-c .
3. Умножьте на три числа из шага 2.
4. Умножить результат на s .
5. Извлеките квадратный корень из результата .
6. Это площадь вашего треугольника — молодец! Используемый нами метод называется Формула Герона .

Как найти площадь треугольника по углам?

Вы не можете определить площадь треугольника, если знаете только углы. Это потому, что существует бесконечно много треугольников с одинаковыми углами . Вы должны знать хотя бы одну сторону (или высоту) треугольника, чтобы определить его площадь.

Как вычислить площадь прямоугольного треугольника?

Чтобы вычислить площадь прямого угла, вам нужно всего лишь умножить длины катетов вашего треугольника, а затем разделить результат на 2. Например, если катетов 3 дюймов и 4 дюймов, тогда площадь равна 3 × 4/2 = 12/2 = 6 дюймов кв.

Чему равна площадь равностороннего треугольника со стороной 10?

Площадь примерно 43,3 . Точный ответ: 25 × √3 . Чтобы получить этот ответ, вспомните формулу площади равностороннего треугольника со стороной a : площадь = a ² × √3 / 4 .