Перегородки из гкл: Перегородки из гипсокартонных листов (ГКЛ). Ремонт своими руками. Статьи о недвижимости, строительстве и ремонте. СИБДОМ

Перегородки из гипсокартона и стекла — перегородки из ГКЛ звукоизолирующие и теплоизолирующие

Перегородки из гипсокартона – это экономичный способ разделения пространства на зоны. Перегородки из ГКЛ применяются как в офисах, торговых центрах, так и в жилых помещениях.

• Универсальность
• Дизайн
• Теплоизоляция, звуко- и шумоизоляция
• Подходят для любого помещения
• Совершенство ГКЛ перегородок
• Конструкции перегородок из ГКЛ
• Звукопоглощающие материалы для ГКЛ

Универсальность

Перегородки из ГКЛ легко и быстро монтируются, не требуют специальных технических условий.

Основой перегородок из гипсокартона является металлический каркас, смонтированный из стальных профилей. Полотна формируются из гипсокартоновых листов, универсальные свойства которых позволяют изгибать их, придавая различные конфигурации.

Дизайн

В конструкцию легко монтируются окна, двери, возможно создавать световые проемы. Перегородки из ГКЛ можно комбинировать со стеклом, что придает конструкции изящество. Поверхность перегородок можно декорировать различными материалами, придать различную цветовую гамму конструкции, нанести рисунок или логотип. Таким образом, перегородки из ГКЛ способны воплощать самые смелые дизайнерские фантазии в жизнь.

Теплоизоляция, звуко- и шумоизоляция

Для повышения тепло- и звукоизоляции при монтаже перегородок из ГКЛ используют пенополистирол, который устойчив к различным температурам и влажности. Благодаря этому, перегородки из ГКЛ можно устанавливать в сантехнических зонах, бассейнах, тренажерных залах и саунах.

Перегородки из ГКЛ обладают надежностью и прочностью, огнестойки и нетоксичны.

Популярности этого вида перегородок способствовала простота и надежность конструкции, которая с легкостью может быть установлена практически в любом помещении. Монтаж стены из гипсокартона не потребует крупных расходов и трудоемких подготовительных работ. Установка перегородок происходит в достаточно сжатые сроки, что позволяет вести внутренние строительные работы ускоренными темпами. Среди других преимуществ гипсокартонных конструкций:

• легкий вес при высокой несущей способности;
• пожаробезопасность;
• влагоустойчивость;
• идеальная поверхность, не требующая дополнительной обработки;
• возможность легко скрыть возможные коммуникации;
• «сухая» технология установки;
• возможность создания любых конфигураций;
• простота монтажа.

Кроме этого, гипсокартонные конструкции смогут при необходимости обеспечить дополнительную звукоизоляцию, и помогут создать в помещении комфортную для работы обстановку.

Подходят для любого помещения

В зависимости от назначения помещения, при разделении его на зоны могут использоваться перегородки с одно-, двух- или трехслойной обшивкой. Для того, чтобы надежно скрыть имеющиеся инженерные коммуникации, используются конструкции с двойным каркасом. Количество листов обшивки напрямую повлияет на степень звукоизоляции, так же, как и наличие воздушной прослойки и толщина внутреннего звукоизоляционного материала.

Еще одним несомненным плюсом, которым обладают гипсокартонные конструкции — это их достаточно небольшая масса, что немаловажно для домов, где не следует нагружать перекрытия дополнительным весом. Установка перегородок ГКЛ не потребует дополнительных разрешений от соответствующих органов, что позволит произвести монтаж конструкций в короткий срок. 

Экологичность листов ГКЛ, на 93% состоящих из гипса, также играет не последнюю роль при выборе в пользу перегородок из гипсокартона. Легкость материала ГКЛ в обработке позволяет дизайнерам воплощать в интерьерах самые необычные идеи и решения, что не всегда возможно осуществить с другими стройматериалами. К тому же гипсокартонная перегородка не украдет лишних сантиметров полезной площади, что немаловажно в условиях малогабаритных помещений.

Совершенство ГКЛ перегородок

Перегородка из гипсокартона и стекла смотрится необычайно эффектно и способна визуально преобразовать пространство любой комнаты. Такие свойства конструкции придает стекло, создающее в помещении открытую атмосферу. Кроме этого гипсокартонная перегородка со стеклом обладает такими достоинствами, как:

• превосходная светопропускаемость;
• привлекательный внешний вид;
• долговечность;
• простота ухода.

Конструкции перегородок из ГКЛ

В конструкциях из ГКЛ возможно использовать закаленное стекло различной фактуры. Прозрачное стекло подарит ощущение пространства и воздуха в любой, самой маленькой комнате. Конструкция с прозрачными стеклами часто используется в офисных помещениях. С помощью гипсокартонныхперегородок и стекла любой, самый скромный офис превратится в стильное пространство, оборудованное согласно американским стандартам.

Перегородка из гипсокартона со стеклом станет отличным решением для любого современного интерьера. Изысканность обстановке придаст матовое стекло, чья нежная фактура создаст в атмосфере комнаты особенное настроение. Пропускающее солнечный свет матовое стекло, тем не менее, способно четко разделить помещение на функциональные зоны, каждая из которых будет хорошо освещена.

Эксклюзивные нотки внесет в интерьер стекло с необычными узорами. Выбирая рисунок, следует строго придерживаться стилистики дизайна комнаты. И тогда стеклянная перегородка станет гармоничным и эффектным дополнением обстановки.

Витражное стекло снова вернулось в моду. Особенно изысканно перегородки с витражным стеклом будут смотреться в интерьере модерн, однако для в аристократичной классике также найдется место для витража, выдержанного в спокойной цветовой гамме.

Если позволяет площадь, стоит рассмотреть вариант с установкой радиальных перегородок. Оригинальные полукруглые перегородки со стеклом полностью изменят конфигурацию комнаты, придадут ей необычный вид. Визуально расширить пространство помещения поможет зеркальное стекло в перегородке. Такое нестандартное решение поможет повлиять на зрительное восприятие интерьера, создаст в комнате нарядную атмосферу.

Дополнительным штрихом может стать оригинальная подсветка, которую легко встроить вгипсокартонную стенку. Подсвеченное стекло будет смотреться необычайно эффектно, и придаст интерьеру роскошный вид.

Звукопоглощающие материалы для ГКЛ

Низкий уровень шума в помещении является обязательным условием для комфортной работы и отдыха человек. С помощью гипсокартонных перегородок возможно добиться отличной шумоизоляции, при условии комплексного подхода к решению проблемы. Ошибочным будет полагать, что только толщина перегородок сможет повлиять на понижение шума в помещении.

Отличного результата возможно добиться, размещая под обшивку ГКЛ различные звукопоглощающие материалы, такие, как шумопоглощающие плиты и звукоизоляционные мембраны. Акустическая мембрана представляет собой полимерное полотно с войлочными ворсинками. Принцип ее работы основан на поглощении звуковых волн, благодаря особенной структуре материала и войлочному покрытию. Дополнением к акустической мембране может стать какой-либо пористый материал, благодаря чему шумоизоляционные характеристики гипсокартонных перегородок значительно возрастают.

Плиты на основе стекловолокна также могут выступить в качестве звукоизолятора. Материал великолепно защитит помещение от проникновения шума. К тому же стекловолоконные плиты практичны, долговечны. и не подвержены гниению. Кроме этого они обладают отличными противопожарными характеристиками.

Панели из каменной ваты с однородной структурой обеспечат отличное звукопоглощение, рассеивая звуковые волны. Материал экологически чист и пожаробезопасен.

Достаточно востребованными материалами являются пенополиуретановые и полиэфирные маты. Их также достаточно часто применяют при возведении гипсокартонных конструкций. В качестве шумоизоляционного средства также возможно использовать любые материалы на основе минеральной ваты.

Перегородки из ГКЛ обладают надежностью и прочностью, огнестойки и нетоксичны.

Рейтинг

Рассчитайте стоимость онлайн

За 11 шагов

Рассчитайте стоимость стеклянных конструкций за 11 шагов онлайн

• Стеклянные перегородки
• Стеклянные двери
• Стеклянные ограждения и перила
• Душевые кабины
• Зеркала

Начать расчет

Перегородки из гипсокартона KNAUF, С111,С112,С115,С116

mathlib/partition.

lean на мастере · leanprover-community/mathlib · GitHub

.

	/-
	Copyright (c) 2020 Бхавик Мехта. Все права защищены.
	Выпущено под лицензией Apache 2.0, как описано в файле LICENSE.
	Авторы: Бхавик Мехта
	-/
	импортная комбинаторика.состав
	импорт data.nat.parity
	импорт тактики.apply_fun
	/-!
	# Разделы
	> ЭТОТ ФАЙЛ СИНХРОНИЗИРУЕТСЯ С MATHLIB4.
	> Любые изменения в этом файле требуют соответствующего PR для mathlib4.
	Разбиение натурального числа `n` — это способ записи `n` в виде суммы положительных целых чисел, где
	порядок не имеет значения: две суммы, отличающиеся только порядком своих слагаемых, считаются
	тот же раздел. Это понятие тесно связано с понятием композиции `n`, но в композиции
	из `n` порядок имеет значение.
	Слагаемое раздела называется частью.
	## Основные функции
	* `p : partition n` представляет собой структуру, состоящую из мультимножества целых чисел, все положительные и
	в сумме дают `n`.
	## Детали реализации
	Основная мотивация для этой структуры и ее API — показать теорему Эйлера о разбиении и
	связанных результатов.
	Представление раздела в виде мультимножества очень удобно, так как мультимножества очень гибкие и
	уже имеют хорошо проработанный API.
	## Метки
	Раздел
	## Ссылки
	wikipedia.org/wiki/Partition_(number_theory)>
	-/
	переменных {α : Тип*}
	открытый мультисет
	open_locale большие_операторы
	пространство имен nat
	/— Раздел `n` представляет собой мультимножество положительных целых чисел, суммирующихся с `n`. -/
	@[расширение, производное decidable_eq] раздел структуры (n : ℕ) :=
	(детали: набор ℕ)
	(parts_pos : ∀ {i}, i ∈ parts → 0 < i)
	(сумма_частей : сумма_частей = n)
	раздел пространства имен
	/— Композиция вызывает разделение (просто преобразуйте список в мультимножество). -/
	def of_composition (n : ℕ) (c : состав n) : раздел n :=
	{ части := c. blocks,
	parts_pos := λ i привет, c.blocks_pos привет,
	part_sum := by rw [multiset.coe_sum, c.blocks_sum] }
	лемма of_composition_surj {n : ℕ} : function.surjective (of_composition n) :=
	начало
	ринтро ⟨b, hb₁, hb₂⟩,
	rcases quotient.exists_rep b с ⟨b, rfl⟩,
	уточнить ⟨⟨b, λ i привет, hb₁ привет, _⟩, partition.ext _ _ rfl⟩,
	simpa с использованием hb₂
	конец
	/—
	Учитывая мультимножество, сумма которого равна `n`, построить разбиение `n` с тем же мультимножеством, но
	без нулей.
	-/
	— Аргумент `n` здесь оставлен явным, поскольку он полезен в доказательствах тактического режима для генерации
	— доказательство обязательства `l.sum = n`.
	def of_sums (n : ℕ) (l : мультимножество ℕ) (hl : l.sum = n) : раздел n :=
	{ частей := л.фильтр (≠ 0),
	parts_pos := λ i hi, nat.pos_of_ne_zero $ путем применения of_mem_filter hi,
	частей_сумма :=
	начало
	есть lt : l. filter (= 0) + l.filter (≠ 0) = l := filter_add_not _ l,
	apply_fun multiset.sum в lt,
	есть lz : (l.filter (= 0)).sum = 0,
	{ rw multiset.sum_eq_zero_iff,
	просто },
	simpa [lz, hl] с использованием lt,
	конец }
	/— `Мультимножество ℕ` индуцирует разбиение своей суммы. -/
	def of_multiset (l : мультимножество ℕ) : раздел l.sum :=
	of_sums_l rfl
	/— Раздел ровно одной части. -/
	def indiscrete_partition (n : ℕ) : раздел n :=
	of_sums n {n} rfl
	instance {n : ℕ} : обитаемый (раздел n) := ⟨indiscrete_partition n⟩
	/—
	Количество раз, когда положительное целое число `i` встречается в разделе `of_sums n l hl`, одинаково
	как количество раз, которое оно появляется в мультимножестве `l`.
	(Для `i = 0`, `partition.non_zero` в сочетании с `multiset.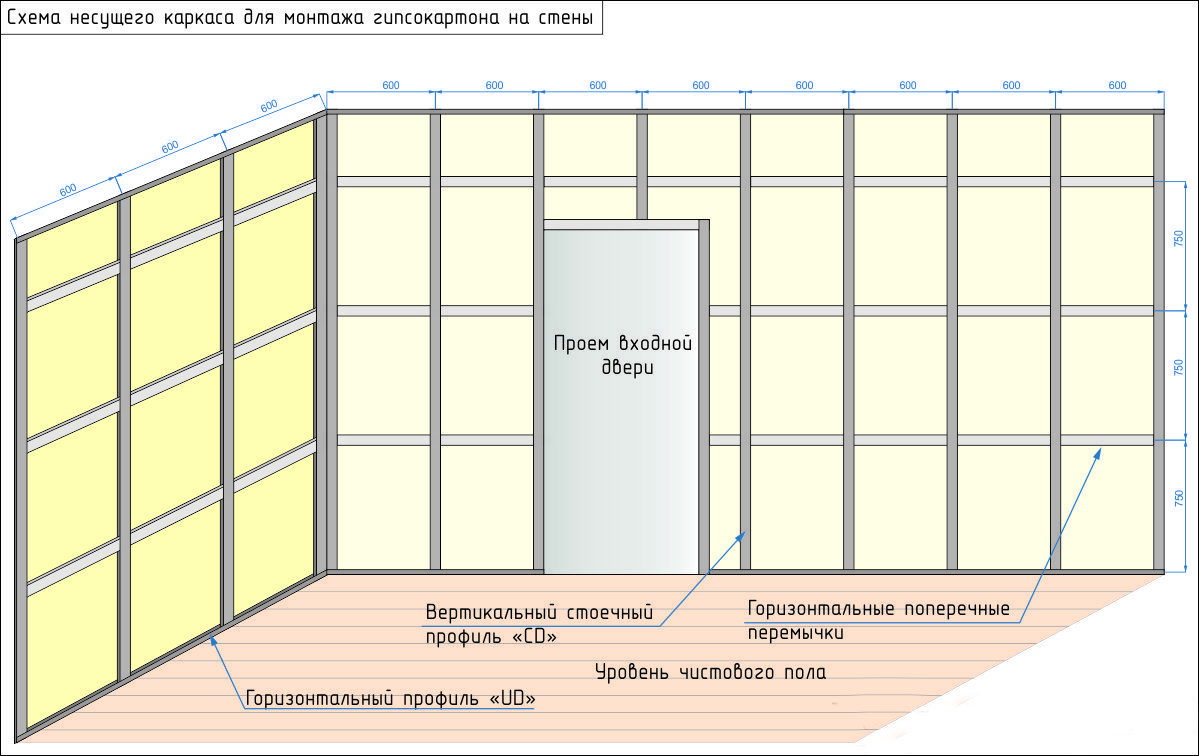 count_eq_zero_of_not_mem` дает
	вместо этого `0`.)
	-/
	лемма count_of_sums_of_ne_zero {n : ℕ} {l : мультимножество ℕ} (hl : l.sum = n) {i : ℕ} (hi : i ≠ 0) :
	(of_sums n l hl).parts.count i = l.count i :=
	count_filter_of_pos привет
	лемма count_of_sums_zero {n : ℕ} {l : мультимножество ℕ} (hl : l.sum = n) :
	(of_sums n l hl).parts.count 0 = 0 :=
	count_filter_of_neg (λ h, h rfl)
	/—
	Покажите, что существует конечное число разделов, рассмотрев сюръекцию от композиций до
	разделов.
	-/
	экземпляр (n : ℕ) : fintype (раздел n) :=
	fintype.of_surjective (of_composition n) of_composition_surj
	/— finset тех разделов, в которых каждая часть нечетная. -/
	деф шансы (n : ℕ) : finset (раздел n) :=
	finset.univ.filter (λ c, ∀ i ∈ c.parts, ¬ четное i)
	/— Финсет тех разделов, в которых каждая часть используется не более одного раза. -/
	различающихся по определению (n : ℕ) : finset (раздел n) :=
	finset.univ.filter (λ c, c.parts.nodup)
	/— finset тех разделов, в которых каждая часть является нечетной и используется не более одного раза. -/
	def odd_distincts (n : ℕ) : finset (раздел n) := шансы n ∩ отличные n
	конец перегородки
	конец нат

Исай Шур, Генри Олдер и разделы — МАТЕМАТИЧЕСКИЕ ЗНАЧЕНИЯ

Автор: Дэвид Брессоуд @dbressoud

Дэвид Брессоуд — почетный профессор ДеВитта Уоллеса в Макалестерском колледже и бывший директор Конференционного совета по математическим наукам

MAA только что опубликовал Решение проблем предварительного исчисления с помощью исчисления II Последовательность с помощью тематических исследований , том Notes, обобщающий результаты проекта, спонсируемого NSF, Прогресс в исчислении 9 0689 , тематические исследования вмешательств в последовательности Precalculus через Calculus II . Доступен по адресу https://www.maa.org/sites/default/files/pdf/pubs/books/members/NTE92.pdf . Введение с описанием исследования и содержанием этого тома доступно по адресу https://macalester.edu/~bressoud/misc/PtC-Introduction.pdf.

Задача: Докажите, что количество способов записать целое число в виде суммы целых чисел, сравнимых с +1 или –1 по модулю 6, равно количеству способов записать это целое число в виде суммы различных целых чисел. не менее чем на 3, причем кратные 3 отличаются не менее чем на 6.

Например, есть шесть разделов из 12, удовлетворяющих первому ограничению: 11+1, 7+5, 7+1+1+1+1+1, 5+5+1+1, 5+1+1. +1+1+1 +1+1 и 1+1+1+1+1+1+1+1+1+1+1+1. Есть также шесть разбиений числа 12, которые удовлетворяют второму: 12, 11+1, 10+2, 9+3, 8+4 и 7+3+1.

Несколько слов об этой проблеме, прежде чем я перейду к своей истории: Эйлер показал, что количество способов записать целое число в виде суммы нечетных целых чисел (конгруэнтных +1 или –1 по модулю 4) равно количество способов записи этого числа в виде суммы различных целых чисел (отличающихся не менее чем на 1). Как представлено в моей последней колонке, q -серийные тождества, открытые независимо Л. Дж. Роджерсом и С. Рамануджаном, подразумевают, что количество способов записи целого числа в виде суммы целых чисел, конгруэнтных +1 или –1 по модулю 5, равно количеству способов записи этого целого числа. в виде суммы целых чисел, отличающихся не менее чем на 2. Равенство, данное в задаче, которая была обнаружена Иссаем Шуром в 1926 году, похоже, соответствует этой схеме. Шур наиболее известен своими работами в области теории представлений, но он также внес значительный вклад в комбинаторику и теорию чисел, включая теорию разделов, где он независимо открыл тождества Роджерса-Рамануджана.

Исай Шур (1875–1941)

Возникает искушение попытаться распространить эти тождества на модуль 7. Кажется, что ничто сравнимое не работает ни там, ни для любого большего модуля. Это яркий пример сильного закона малых чисел Ричарда Гая : «Недостаточно малых чисел, чтобы удовлетворить множество предъявляемых к ним требований». Тот факт, что закономерность проявляется в нескольких небольших случаях, не обязательно означает, что она продолжается. Как Бэзил Гордон должен был обнаружить в 1961 и, как я объясню позже в этой колонке, плодотворное обобщение на более высокие модули было связано не с тем, какие классы вычетов сохраняются, а скорее с тем, какие классы вычетов исключаются.

Генри Алдер (1922–2002)

В 1956 году Генри Алдер выдвинул гипотезу о более слабом расширении теоремы Шура о том, что количество разбиений n на части, отличающиеся не менее чем на d , всегда больше или равно количеству разбиений n на части, конгруэнтные +1 или –1 по модулю d +3. В 1971 г. Джордж Эндрюс доказал это для случаев, когда d на единицу меньше степени 2. В 2004 г. Э Джа Йи установил истинность этой гипотезы для всех d , больших 31. Остальные случаи были доказаны в 2011 г. Клаудия Алфес, Мари Джеймсон и Роберт Дж. Лемке Оливер. См. ссылки в конце этой колонки.

Генри Алдер был преподавателем Калифорнийского университета в Дэвисе. Он занимал пост секретаря МАА с 19с 60 по 1975 год и в качестве президента с 1977 по 1979 год. Я включил теорему Шура, потому что в самом начале своей карьеры я обнаружил простое доказательство, достаточно привлекательное, чтобы Генри Алдер в своем выступлении на пенсию в качестве президента МАА включил его в свое выступление. Я прибыл.

Я возвращаюсь к своему рассказу лета 1976 года. Найдена основная часть результатов, которые легли в основу моей докторской диссертации. Гроссвальд порекомендовал мне посетить летние математические встречи, которые проводились в том же году в Университете Торонто, чтобы рассказать о своих открытиях. Это был незапрошенный 10-минутный разговор от совершенно неизвестного, что обычно является признаком того, что будет довольно небольшая аудитория. Что еще хуже, моя презентация противоречила последней презентации Аппеля и Хокина их доказательства теоремы о четырех цветах, компьютерного доказательства того, что любую плоскую карту всегда можно раскрасить четырьмя цветами без необходимости двух смежных областей. разделяют тот же цвет.

Насколько я помню, в аудитории во время моей презентации было три человека: человек, который говорил передо мной и которому нужно было представить мое выступление, человек, который должен был говорить после меня и который нервно ждал своей очереди, и Дик Аски .

Дик просмотрел рефераты и выбрал мою работу как демонстрирующую потенциал. Затем он провел со мной остаток дня, объясняя, как моя работа связана с теорией серии q , и рассказывая мне, что мне нужно прочитать, особенно книгу Джорджа Эндрюса «9».0689 The Theory of Partitions , вышедшей в 1976 году, и Theory and Applications of Special Functions , сборник статей, представленных в 1976 году на специальном семинаре в Университете Висконсина. В частности, он направил меня к статье Джорджа Эндрюса «Проблемы и перспективы основных гипергеометрических функций», которую я приступил к подробному изучению.

Дик тоже считал, что мне будет полезно познакомиться с Джорджем. Я точно не знаю, как это произошло. Гроссвальд знал Эндрюса. У них был один и тот же научный руководитель Ганс Радемахер. Они пересекались в Пенне, где Джордж был аспирантом, а Гроссвальд — инструктором, и знали работы друг друга. Для Гроссвальда было вполне естественно пригласить Эндрюса, который находился недалеко от Пенсильванского университета, приехать в Темпл, чтобы представить коллоквиум, что он и сделал в начале 19-го века.77. Дик, который был очень близок с Джорджем, мог внести предложение.

В любом случае, Джордж пришел, рассказал о q -серии и представил множество открытых задач. Написание моей диссертации к настоящему времени было почти завершено, так что я мог свободно погрузиться в проблемы Джорджа. Я нашел решения для нескольких из них.

В то время перспективы моей работы не были радужными. Я был на Совместных Математических Совещаниях и вышел только с одной многообещающей зацепкой. Мне показалось, что SUNY Binghamton заинтересовался мной. Прежде чем они приняли какое-либо решение, я получил предложение от Penn State. Как я позже узнал, математический факультет штата Пенсильвания не нанимает никого, кто не имеет сторонника среди своих преподавателей, а влиятельный сторонник, такой как Джордж, имеет большой вес. Мне предложили двухгодичную гостевую должность.

Та весна выдалась на редкость урожайной. К июню я доказал один из своих самых значительных результатов — обобщение тождеств Роджерса-Рамануджана, распространяющееся на любой модуль. В 1961 году Бэзил Гордон опубликовал расширение тождеств Роджерса-Рамануджана на любой нечетный модуль (рис. 1). К 1967 году у Джорджа Эндрюса был случай, когда модуль конгруэнтен 2 по модулю 4, а значение r , дающее два исключенных класса остатков, отличных от 0, является нечетным. Он включил случай, когда модуль равен 2 по модулю 4 и 9.0689 r есть даже в его 1976 The Theory of Partitions . Весной 1977 года, готовясь к поступлению в Государственный колледж, я обнаружил и доказал случай произвольного четного модуля (рис. 2).

Рис. 1. Теорема, опубликованная Бэзилом Гордоном в 1961 г.

Рис. 2. Мое обобщение теоремы Гордона, опубликованное в 1979.

Это, в свою очередь, привело к многочисленным обобщениям и расширениям этих тождеств и их аналитических основ, которые я опубликовал в качестве мемуаров AMS в 1980 году. -трековая позиция в Penn State.

Мой прогресс был до крайности необычным. Я прошел путь от докторской степени в Исследовательском университете 2 до постоянной должности, а затем и полного профессора в одном из 25 элитных государственных Исследовательских университетов 1. Я понимаю, насколько моя последующая карьера была построена на вмешательстве Дика и Джорджа. Я навсегда у них в долгу.

Этот опыт преподал мне два важных урока относительно выбора научного руководителя докторской диссертации. Во-первых, это должен быть кто-то, с кем вы можете легко установить контакт. Конкретная область, в которой человек хочет работать, имеет гораздо меньшее значение. На самом деле Гроссвальд специально предупредил меня, чтобы я не ожидал, что буду продолжать работать в области, в которой получил докторскую степень. Докторская степень — это сигнал о том, что человек способен внести существенный, оригинальный вклад в математику в широком смысле, не более того. Во-вторых, чрезвычайно важна репутация консультанта докторской диссертации и то, насколько он или она подключены к сети исследователей. Это никогда не должно перевешивать первое соображение. Из многих уважаемых математиков получаются паршивые советники. Но это важное соображение для начала успешной карьеры.

Первый шаг в установлении соответствия между двумя типами разбиений состоит в том, чтобы отметить, что целые числа, конгруэнтные +1 или –1 по модулю 6, являются просто нечетными целыми числами, которые не делятся на 3. Эйлер использовал производящие функции, чтобы установить, что количество разбиений n на нечетные целые числа равно количеству разбиений на различные целые числа. Харди и Райт дали хорошее комбинаторное доказательство. Любое доказательство показывает, что исключение кратных 3 среди нечетных целых чисел означает исключение кратных 3 среди различных целых чисел. Поскольку оно чисто комбинаторное, я приведу доказательство Харди и Райта. 90) умножить на нечетное целое число (которое может быть 1), которое я буду называть нечетным корнем . Мы берем различные целые числа и группируем те, которые имеют один и тот же нечетный корень. Сумма соответствующих степеней двойки дает уникальное целое число, которое будет обозначать, сколько раз это нечетное число появляется при разбиении на нечетные целые числа. Например, разбиение на отдельные целые числа 1 + 4 + 5 + 6 + 8 + 20 группируется как (1 + 4 + 8)*1 + (2)*3 + (1 + 4)*5, что дает тринадцать единиц, две тройки и пять пятерок. Это однозначно обратимо. Если среди различных целых чисел нет кратных 3, среди нечетных чисел не будет кратных 3, и наоборот.

Следующим произведением был мой вклад. Учитывая разбиение на различные целые числа, не кратные 3, мы находим самую большую пару, которая отличается менее чем на 3, и складываем их вместе, затем продолжаем движение вниз среди оставшихся целых чисел, пока не найдем следующую самую большую пару с разницей меньше 3, и снова добавить их вместе. Продолжайте до тех пор, пока все числа, не делящиеся на 3, будут отличаться как минимум на 3. В каждой паре обязательно одно из чисел сравнимо с +1, а другое –1 по модулю 3, поэтому каждая сумма делится на 3. Рассмотрим следующий пример. ,

1+2+4+7+8+14 -> 1 + 6 + 15 + 14. Отнимаем 3 от второго числа, 6 от третьего и вообще 3( k –1) от к тыс. Размещаем оставшиеся целые числа в порядке возрастания, затем прибавляем 3 ко второму, 6 к третьему и так далее,

1 + 6 + 15 + 14 => 1 + 3 + 9 + 5 => 1 + 3 + 5 + 9 => 1 + 6 + 11 + 18.

Все эти числа будут отличаться не менее чем на 3, а кратные 3 должны отличаться не менее чем на 6, поскольку на промежуточном этапе кратные 3 различны. Что может быть не сразу очевидно, так это то, что эта процедура однозначно обратима.

К сожалению, проверка, которую мне пришлось использовать, показанная на рисунках 3, 4 и 5, не так проста, как хотелось бы. Заметьте, что сама теорема и мое доказательство носят более общий характер.

Для 0 < r < m /2 количество разбиений n на отдельные части, конгруэнтные + r или – r по модулю m равно количеству разделов n на части, равные 0, + r , или – г по модулю м , которые отличаются не менее чем на м , с частями, кратными м , отличающимися не менее чем на 2 м . То же самое соответствие работает и для этого более общего случая. Вы можете найти полное утверждение и доказательство в моей статье «Комбинаторное доказательство теоремы Шура 1926 года о разделении», которая была опубликована в Proceedings of the American Mathematical Society , vol. 79, 1980, 338–340.

Должен добавить, что после того, как она была опубликована, я понял, что статья мне не понравилась так, как она написана. В нем отсутствуют примеры или какое-либо ощущение простоты идеи. Именно это подчеркивал Алдер в своем выступлении, игнорируя уникальную обратимость и просто утверждая ее истинность. Конечно, это была публичная презентация, а не строгое доказательство. Хотя опубликованное исследование должно быть логически завершенным, оно также должно отражать дух доказательства. Мне не удалось сделать это в этой статье, но я научился этому неправильному представлению. В каком-то смысле эта колонка — моя попытка исправить эту ошибку

Рисунки 3–5. Завершение доказательства теоремы Шура.

Каталожные номера

Ольха, H.L . (1956). № исследовательской задачи. 4, Бюлл. амер. Мат. соц.   62 , 76

Алфес, К., Джеймсон, М. и Лемке Оливер, Р.Дж., (2011), Доказательство гипотезы Альдера-Эндрюса, Проц. АМС , 139 , 63–78.

Эндрюс, Г.Э. (1967). Некоторые новые теоремы о разбиении. J. Комбинаторная теория , 2 , 431–436.

Эндрюс, Г.Э. (1971). О проблеме разбиения Г. Л. Альдера. Pacific J. Math ., 36 , 279–284.

Эндрюс, Г.Э. (1976). Теория разделов . Чтение, Массачусетс: Аддисон-Уэсли.

Брессоуд, Д. (1979). Обобщение тождеств Роджерса-Рамануджана для всех модулей. J. Комбинаторная теория, серия A . 27 , 64–68.

Брессо, Д. (1980). Комбинаторное доказательство теоремы Шура 1926 года о разделении, Proc. АМС , 79 , 338–340.

Брессо, Д. (1980). Аналитические и комбинаторные обобщения тождеств Роджерса-Рамануджана.