Как вычислить прямой угол: Прямой угол — урок. Математика, 2 класс.

Угол между прямой и плоскостью — что это такое? Как найти?

Поможем понять и полюбить математику

Начать учиться

Представьте: на уроке физкультуры вам нужно кинуть мяч точно в нарисованную на стене мишень. «Целься под углом 45°», — советует физрук. Или вы читаете задачу по физике, где солнечные лучи падают на поверхность под углом α. А может быть, вам надо помочь маме в саду и подпереть дверь старой лопатой. Что общего у этих ситуаций?

Правильный ответ такой: все эти случаи можно озаглавить геометрическим понятием «пересечение плоскости прямой под некоторым углом». Об этом мы сегодня и поговорим, а именно:

• рассмотрим главные определения и примеры;

• изучим свойства и теоремы по теме;

• научимся находить угол между прямой и плоскостью.

Определение угла между прямой и плоскостью

Угол между прямой и плоскостью — это угол между прямой и её проекцией на эту плоскость.

Мы уже знакомы с понятиями «угол», «прямая» и «плоскость» (если подзабыли, то можете повторить по нашим материалам). А сейчас давайте вспомним, что такое проекция.

Проекция — это геометрическое изображение на плоскости, полученное проведением перпендикуляров из всех точек данного тела на плоскость.

То есть под углом между прямой и плоскостью в пространстве мы подразумеваем угол между прямой и её отображением на плоскость.

Важное уточнение

Если прямая перпендикулярна плоскости, то можно считать, что угол между ними равен 90°, что следует из определения перпендикулярности прямой и плоскости. Этот случай — самый простой, его мы рассматривать не будем.

Также стоит заметить, что если прямая параллельна плоскости, то у них нет ни одной общей прямой, а значит, угол между ними не определяется.

Как вы думаете, какой тип имеет угол между прямой и плоскостью? Верно, он может быть только острым. Попробуйте доказать это самостоятельно 😊

Реши домашку по математике на 5.

Подробные решения помогут разобраться в самой сложной теме.

Свойства и теоремы

Свойство угла между прямой и плоскостью

Углом между прямой и плоскостью называется наименьший из углов между прямой и произвольной прямой в плоскости.

Попробуем привести доказательство. Для этого нарисуем плоскость и проведём к ней прямую АВ, являющуюся наклонной. Тогда АВ₁ — проекция прямой на плоскость, АН — произвольная прямая, принадлежащая плоскости, а ВН и ВВ₁ — перпендикуляры к плоскости (ВН ⟂ АН, ВВ₁ ⟂ АВ).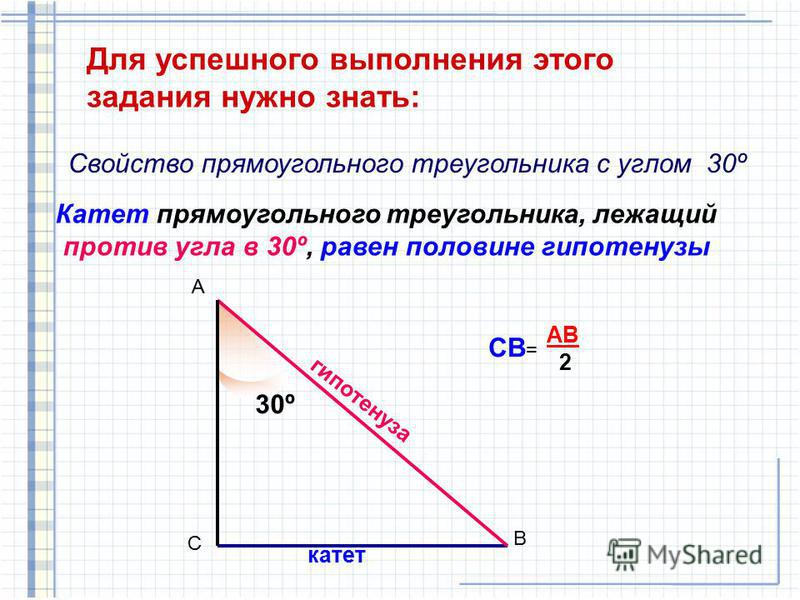 Чтобы лучше представить себе этот объёмный чертеж, можно сделать небольшой макет из сложенного листа бумаги, прислонив его к поверхности стола или тетради.

Чтобы проверить истинность свойства, нам необходимо доказать, что угол ∠ВАВ₁ намного меньше, чем угол ∠ВАН.

Обозначим проблему: значения этих углов, как и других исходных, нам неизвестны. А значит, на помощь может прийти тригонометрия, ведь сравнить углы можно и через их синусы.

Синус — это отношение противолежащего угла к гипотенузе. В таком случае, .

Оба перпендикуляра ВВ₁ и ВН проведены из точки В, но только один из них является кратчайшим расстоянием от точки по плоскости, и это перпендикуляр ВВ1. Так как значения синусов представляют собой дроби с одинаковыми знаменателями, большей будет та, у которой больше знаменатель.

Следовательно, sin ∠BAB1 < sin ∠BAH, ∠BAB1 < ∠BAH.

Теорема

Из двух наклонных, проведённых из одной точки к плоскости, меньшая образует с плоскостью больший угол, и наоборот: угол, образованный большей наклонной, будет меньшим из двух.

Существует множество разных доказательств этой теоремы, но мы сосредоточимся на одном из них.

Для этого изобразим плоскость и точку . Из точки А проведём две наклонные прямые, причем АВ < АС, а также перпендикуляр к плоскости АО.
Докажем, что ∠АВО > ∠АСО.

Стороны ОВ и ОС являются проекциями АВ и АС соответственно. Меньшая прямая имеет меньшую проекцию, а значит, ОВ < ОС.

Отложим на стороне ОС отрезок ОЕ, равный ОВ. Можно ли доказать равенство треугольников АОВ и АОЕ?

В данных треугольниках:

• ОВ = ОЕ (по построению),

• АО — общий катет.

Следовательно, треугольники АОВ и АОЕ равны по двум катетам (или по первому признаку: две стороны и угол между ними). В таком случае равны и соответственные углы: ∠АВО = ∠АЕО.

Угол АЕО является внешним для треугольника АЕС, и по свойству внешнего угла ∠АЕО = ∠АСЕ + ∠САЕ. Не трудно догадаться: раз угол АЕО равен сумме двух других углов треугольника, не смежных с ним, то он больше любого из этих двух углов.

∠АЕО > ∠АСЕ, и так как ∠АЕО = ∠АВО, то ∠АВО > ∠АСЕ.

Что и требовалось доказать. 😎

Как найти угол между прямой и плоскостью

От теории переходим к практике: а как же можно вычислить угол между прямой и плоскостью? Вопрос лёгкий и сложный одновременно. Дело в том, что задач на нахождение угла очень много, и в каждой из них применяется свой алгоритм решения. Большую роль играет предмет и раздел, в котором эта задача приведена: это может быть стереометрия, векторная алгебра и даже физика. Но все эти алгоритмы сводятся к двум методам: геометрическому и алгебраическому или координатному методу. Давайте подробно рассмотрим каждый из них.

Геометрический метод

Чтобы применить геометрический метод, необходимо опустить перпендикуляр на плоскость из точки, принадлежащей исходной прямой. Выясним, чем в этом задании является перпендикуляр, наклонная и проекция, и решим планиметрическую задачку (чаще всего в таких задачах нам будет необходимо найти один из углов прямоугольного треугольника).

Задача 1

Из точки А на плоскость проведены две наклонные АВ и АС и перпендикуляр АО, причём О, В и С — точки пересечения с плоскостью .

Определите, чему равен АО, если СО = 10, ВО = 26, а угол АСО в два раза больше угла АВО.

Решение:

Отметим на стороне ОВ отрезок, равный ОС. Тогда ОС = ОЕ = 10, а ЕВ = 26 – 10 = 16.

Рассмотрим треугольники АСО и АЕО:

• СО = ОЕ (по построению),

• АО — общий катет.

Следовательно, треугольники равны по двум катетам. А значит, угол АСО равен углу АЕО.

Угол АЕО является внешним для треугольника АЕВ, а значит, ∠АЕО = ∠АВЕ + ∠ВАЕ. Так как ∠ АВЕ = , значит, ∠ ВАЕ = 2-=, и треугольник АЕВ — равнобедренный.

Тогда найдём АО через прямоугольный треугольник АОЕ по теореме Пифагора:

.

Ответ: .

Алгебраический метод

Алгебраический метод или метод координат для нахождения угла между прямой и плоскостью основывается на особой формуле. Чтобы использовать его, необходимо определить координаты двух точек, принадлежащих прямой, описать уравнение плоскости и применить формулу. По сути в этом методе мы находим угол между вектором и плоскостью.

,

где (x₁, y₁, z₁) — это координаты первой точки,

(x₂, y₂, z₂) — координаты второй точки,

А, В и С — это координаты в уравнении плоскости Ax + By + Cz + D = 0.

Иначе эти числа называют координатами вектора нормали плоскости.

Тут может возникнуть вопрос: а что, если в задаче даны не координаты точек, а координаты вектора?

В этом случае вспомним, что координаты вектора находятся через разность координат начала и конца. А значит, мы со спокойно душой подставляем эти координаты в формулу вместо (х₂ – х₁), (y₂ – y₁) и (z₂ – z₁).

В некоторых задачах для нахождения угла между прямой и плоскостью вводят понятие направляющего вектора прямой. Направляющий вектор прямой — это любой вектор, не равный нулю, который размещается на данной прямой или же на прямой, параллельной ей.

Координаты этого вектора можно получить из канонического уравнения прямой:

, где направляющий вектор а имеет координаты (a_x, a_y).

Тогда угол между прямой и плоскостью можно вычислить по формуле:

.

Задача 2

Найдите угол между прямой и плоскостью 3x – y – z + 1 = 0.

Решение:

1. Определим координаты направляющего вектора для прямой: (2; –1; 3).

2. Определим координаты вектора нормали плоскости: (3; –1; –1).

3. Подставим координаты в формулу для расчёта синуса угла между плоскостью и прямой:

   .

Задача 3

Найдите угол между плоскостью, заданной уравнением x + 2y + 2z – 4 = 0, и прямой, которой принадлежат точки А (0, 2, –1) и В (–2, 4, –1).

Решение:

1. Определим координаты вектора нормали плоскости: (1; 2; 2).

2. Подставим координаты вектора нормали и координаты точек прямой в формулу:

   .

За короткий промежуток времени мы изучили понятие угла между прямой и плоскостью, доказали теоремы, разобрали способы нахождения угла и решили практические задания. Мы — молодцы! 💪

Думаем, вы понимаете, что эта тема очень важна — с её помощью решаются сложные стереометрические задачи, которые встречаются на ОГЭ и ЕГЭ. Подготовиться к таким серьёзным заданиям помогут курсы профильной математики в онлайн-школе Skysmart. На уроках мы сможем более подробно разобрать задачи с пирамидами и параллелепипедами, а ещё научимся составлять уравнения для любой плоскости. Узнать свои сильные и слабые стороны, составить план обучения и познакомиться с онлайн-платформой можно на вводном уроке — это бесплатно.

Шпаргалки для родителей по математике

Все формулы по математике под рукой

Дарья Вишнякова

К предыдущей статье

Компланарность векторов

К следующей статье

Теоремы, которые точно пригодятся на ЕГЭ

Получите план обучения, который поможет понять и полюбить математику

На вводном уроке с методистом

1. Выявим пробелы в знаниях и дадим советы по обучению

2. Расскажем, как проходят занятия

3. Подберём курс

Измерение углов.

Транспортир. Виды углов / Геометрия / Справочник по математике 5-9 класс

1. Главная
2. Справочники
3. Справочник по математике 5-9 класс
4. Геометрия
5. Измерение углов. Транспортир. Виды углов

Нам известно, что при измерении отрезков, мы сравниваем измеряемый отрезок с отрезком, который принят за единицу измерения (1 мм, 1 см, 1 м и т.д.). Аналогично происходит измерение углов: чтобы измерить угол его сравнивают с углом, который принят за единицу измерения —  с  градусом, записывают так 1°.

Градусная мера угла — это число, которое показывает, сколько раз градус и его части укладываются в данном угле.

Пример:

Градусная мера угла ABC равна . Говорят: «Угол ABC равен 120 градусам». Пишут: .

Транспортир — это измерительный инструмент, который используется для измерения и построения углов. Состоит из линейки (прямолинейной шкалы) и полукруга (угломерной шкалы: внутренней и внешней), который разделен на градусы от 0 до .

Для того чтобы измерить угол, необходимо совместить вершину угла с центром транспортира, при этом одна из сторон угла должна пройти через нулевое деление шкалы, тогда вторая сторона угла укажет градусную меру угла.

Пример: Измерим угол ABC, для этого совместим точку B с центром транспортира, и расположим транспортир так, чтобы сторона BC прошла через нулевое деление шкалы (обратите внимание отсчёт угла ведётся по той шкале, через нулевое деление которой пройдет одна из сторон угла: в нашем случае по внутренней шкале).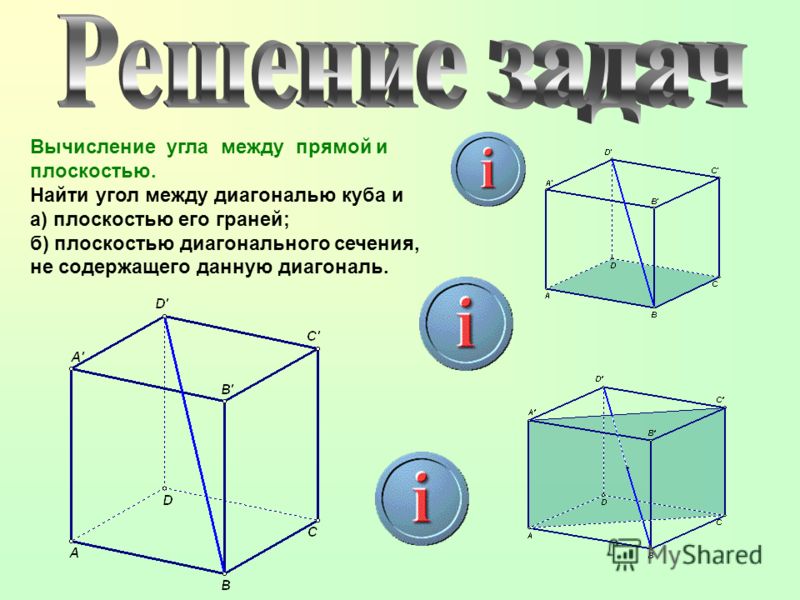

Вторая сторона при этом, как мы видим, проходит через деление шкалы 120, значит: .

Свойства:

• Равные углы имеют равные градусные меры.
• Меньший угол имеет меньшую градусную меру.
• Развернутый угол равен .
• Неразвернутый угол меньше .
• Если луч делит угол на два угла, градусная мера всего угла равна сумме градусных мер этих углов, т.е. на рисунке ниже

         АОС = АОВ + ВОС.

Виды углов:

1. Острый угол — угол, градусная мера которого меньше 90°.

2. Прямой угол — угол, градусная мера которого равна 90°.

3. Тупой угол — угол, градусная мера которого больше 90°, но меньше 180°.

4. Развернутый угол — угол, градусная мера которого равна 180°.

Биссектриса развернутого угла делит его на два угла, градусная мера каждого из которых равна 90⁰.

АОС — развернутый, ОВ — биссектриса, АОВ = ВОС = 90⁰.

Советуем посмотреть:

Отрезок

Ломаная

Четырехугольники

Единицы измерения площадей. Свойства площадей

Прямоугольник, его периметр и площадь. Ось симметрии фигуры

Квадрат. Периметр и площадь квадрата.

Многоугольники. Правильные многоугольники. Равенство фигур.

Плоскость

Прямая

Луч

Шкалы и координаты

Прямоугольный параллелепипед. Пирамида.

Объем прямоугольного параллелепипеда

Куб. Площадь поверхности куба

Куб. Объем куба

Угол. Обозначение углов

Прямой и развернутый угол

Чертежный треугольник

Треугольник и его виды

Окружность, круг, шар

Цилиндр, конус

Отрезок-xx

Геометрия

Правило встречается в следующих упражнениях:

5 класс

Задание 1650,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1774,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Номер 301,
Мерзляк, Полонский, Якир, Учебник

Номер 303,
Мерзляк, Полонский, Якир, Учебник

Номер 499,
Мерзляк, Полонский, Якир, Учебник

Номер 595,
Мерзляк, Полонский, Якир, Учебник

Номер 1029,
Мерзляк, Полонский, Якир, Учебник

Номер 1189,
Мерзляк, Полонский, Якир, Учебник

Номер 1190,
Мерзляк, Полонский, Якир, Учебник

Номер 2,
Мерзляк, Полонский, Якир, Учебник

6 класс

Номер 219,
Мерзляк, Полонский, Якир, Учебник

Номер 686,
Мерзляк, Полонский, Якир, Учебник

Номер 714,
Мерзляк, Полонский, Якир, Учебник

Номер 1233,
Мерзляк, Полонский, Якир, Учебник

Номер 1234,
Мерзляк, Полонский, Якир, Учебник

Номер 1236,
Мерзляк, Полонский, Якир, Учебник

Задание 738,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 773,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1425,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1534,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

7 класс

Номер 759,
Мерзляк, Полонский, Якир, Учебник

Формула прямоугольного треугольника

— Что такое формула прямоугольного треугольника? Примеры

 Треугольник – это замкнутая фигура или фигура с 3 сторонами, 3 углами и 3 вершинами. Для формул прямоугольного треугольника свойства должны быть более конкретными. Если какой-либо из углов треугольника является прямым углом (составляет 90º), треугольник называется прямоугольным треугольником или просто прямоугольным треугольником. Формулы прямоугольного треугольника помогут вам выполнять различные вычисления, связанные с периметром, площадью и т. д. прямоугольного треугольника.

Что такое формулы прямоугольного треугольника?

Прямоугольный треугольник — это треугольник, один из внутренних углов которого равен 90 градусов. Формулы прямоугольного треугольника используются для вычисления периметра, площади, высоты и т. д. прямоугольного треугольника с использованием трех его сторон.

Формула прямоугольного треугольника

Различные формулы, связанные с прямоугольным треугольником:

• Теорема Пифагора — Формула

Определение теоремы Пифагора показывает отношение между тремя сторонами прямоугольного треугольника. Квадрат гипотенузы равен сумме квадратов двух других катетов.

    (Гипотенуза) ²  =  (Перпендикуляр) ²  + (Основание) ²

• Формула площади прямоугольного треугольника

Формула для вычисления площади прямоугольного треугольника задается следующим образом:

     Площадь = 1/2 × Основание × Высота = 1/2 × b × h

, где высота,h равна длине перпендикуляра сторона треугольника.

• Формула периметра прямоугольного треугольника

Формула для вычисления площади прямоугольного треугольника задается как:

    Периметр = a + b + c​​​

, где a, b и c — три стороны треугольника.

Разбивайте сложные концепции с помощью простых визуальных средств.

Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций.

Записаться на бесплатный пробный урок

Примеры использования формул прямоугольного треугольника

Пример 1: Длина основания и перпендикуляра прямоугольного треугольника составляет 6 дюймов и 8 дюймов соответственно. Найти:

• Длина гипотенузы
• Периметр треугольника
• Площадь треугольника

Решение:      

Найти:

Дано: длина основания = 6 дюймов, длина перпендикуляра = 8 дюймов 2  + (Перпендикуляр) ²  

(Гипотенуза) ²  = 6 ²  + 8 ² = 100

Гипотенуза = √100 = 10 из

ii) Используя формулу периметра прямоугольного треугольника,

Периметр = сумма всех сторон

Периметр = 6 + 8 + 10 = 24 из

2 iii) Используя формулу

3 формула площади треугольника,

Площадь = (1/2) × b × h

= (1/2) × 6 × 8

= 24 в ²

Ответ: Гипотенуза прямоугольного треугольника = 10 дм, периметр прямоугольного треугольника = 24 дм, а площадь прямоугольного треугольника = 24 дм ² .

Пример 2: Высота и гипотенуза прямоугольного треугольника равны 12 дюймам и 13 дюймам соответственно. Найдите его площадь.

Решение:        

Чтобы найти: площадь прямоугольного треугольника

Дано: высота = 12 дюймов, гипотенуза = 13 дюймов ²  + (12) ²

(база) ²  = (13) ²  — (12) ² = 25

Основание = √25 = 5 в

Используя формулу площади треугольника,

Площадь = (1/2) × b × h

Площадь = (1/2) × 5 × 12

Площадь = 30 в ²

Ответ: Площадь прямоугольного треугольника = 30 в ²

30 единиц, высота 12 единиц, гипотенуза 13 единиц

Решение:  

Чтобы найти: Площадь прямоугольного треугольника

Дано: периметр = 30 единиц, гипотенуза = 13 единиц, высота = 12 единиц

Мы знаем, что периметр = основание + гипотенуза + высота

30 единиц = 13 + 12 + основание

Следовательно, основание = 30 — 25 = 5 единиц

Площадь = 1/2bh = 1/2 (5 × 12) = 30 квадратных единиц.

Ответ:  Площадь прямоугольного треугольника = 30 единиц ²

Часто задаваемые вопросы о формулах прямоугольного треугольника

Что такое формула прямоугольного треугольника в геометрии?

В геометрии формулы прямоугольного треугольника — это формулы прямоугольного треугольника, которые используются для вычисления периметра, площади, высоты и т. д. треугольника с использованием трех его сторон — основания, высоты и гипотенузы. Эти формулы задаются следующим образом:

• Теорема Пифагора — Формула: (Гипотенуза) ²  =  (Перпендикуляр) ²  + (Основание) ²
• Формула площади прямоугольного треугольника: Площадь = 1/2 × Основание × Высота
• Формула периметра прямоугольного треугольника = Сумма длин трех сторон

Каково применение формулы прямоугольного треугольника?

Существует множество применений прямоугольного треугольника в реальной жизни, наиболее распространенным является его использование в области тригонометрии, поскольку отношение между его углами и сторонами составляет основу тригонометрии. Он также используется в области строительства и машиностроения.

Как рассчитать площадь прямоугольного треугольника, используя формулу прямоугольного треугольника, когда известны его периметр, высота и основание?

Для того, чтобы вычислить площадь прямоугольного треугольника, когда известны его периметр, высота и основание, будем учитывать только два параметра — высоту и основание.

• Шаг 1: Проверьте заданные значения.
• Шаг 2. Подставьте значения высоты h и основания b в формулу площади (1/2)bh

Как найти формулу высоты прямоугольного треугольника?

Высоту прямоугольного треугольника можно рассчитать, учитывая длину основания и высоту. Формула прямоугольного треугольника может быть рассчитана с использованием теоремы Пифагора как, (Гипотенуза) ²  =  (Высота) ²  + (База) ² . Подставьте известные значения и найдите высоту или перпендикуляр прямоугольного треугольника.

Калькулятор прямоугольного треугольника | PI Day

C (Hypotenuse)

Периметр

Угол 1

Угол 2

Угол 3

Вернитесь к калькуляторам. прямоугольный треугольник в верхние поля. Затем калькулятор определит длину оставшейся стороны, площадь и периметр треугольника, а также все углы треугольника.

Как найти площадь и стороны прямоугольного треугольника

Сделай сам

Если мы знаем только две стороны прямоугольного треугольника, мы можем использовать эту информацию, чтобы найти третью сторону, площадь и периметр треугольника и все углы треугольника. Удивительно, правда? Давайте рассмотрим, как мы найдем каждую из этих частей.

Как найти недостающую сторону прямоугольного треугольника

Чтобы найти недостающую сторону прямоугольного треугольника, мы используем знаменитую теорему Пифагора.

Нам нужно быть немного осторожными, чтобы знать, какую сторону мы находим. Прямоугольные треугольники имеют два катета и гипотенузу, которая является самой длинной стороной и всегда находится напротив прямого угла. Когда мы пытаемся найти гипотенузу, мы заменяем две наши известные стороны на a и b . Неважно, какая ножка a , а какая b . Затем мы находим c , складывая квадраты значений a и b и извлечь квадратный корень из обеих частей.

Когда мы пытаемся найти один из катетов, мы вводим известный катет для a и известную гипотенузу для c . Затем мы находим b , используя простую алгебру (вычтем значение a в квадрате с обеих сторон, затем возьмем квадратный корень из обеих сторон).

Как найти площадь прямоугольного треугольника

Чтобы найти площадь прямоугольного треугольника, нам нужно знать только длину двух катетов. Нам вообще не нужна гипотенуза. Это потому, что катеты определяют основание и высоту треугольника в каждом прямоугольном треугольнике. Поэтому мы используем общую формулу площади треугольника (A = основание • высота/2) и подставляем a и b для основание и высота . Итак, наша новая формула для площади прямоугольного треугольника: A = ab/2.

Как найти периметр прямоугольного треугольника

Чтобы найти периметр или расстояние вокруг нашего треугольника, нам просто нужно сложить все три стороны вместе. Если мы знаем только две стороны, нам нужно сначала использовать теорему Пифагора, чтобы найти третью сторону.

Как найти углы прямоугольного треугольника

Чтобы найти углов прямоугольного треугольника, мы используем тригонометрию. Это не так сложно, как кажется. Нам просто нужно найти одну специальную кнопку на наших карманных калькуляторах. Для начала нам нужно знать все длины сторон, поэтому, если мы их еще не знаем, мы сначала воспользуемся теоремой Пифагора, чтобы найти их.

Когда у нас есть все стороны, мы определяем, какой угол мы собираемся найти. Затем мы берем сторону, противоположную этому углу, и делим ее на длину гипотенузы, которая равна стороне 9.0179 с . Это даст нам значение от 0 до 1. Теперь нам просто нужно найти кнопку ARCSIN на нашем калькуляторе, которая часто помечается как SIN ^-1 . Нахождение ARCSIN нашего десятичного значения дает нам угол. Убедитесь, что калькулятор настроен на угловой режим, а не на радианный.

Мы можем повторить этот процесс, чтобы найти другой неизвестный угол в треугольнике, еще раз разделив его противоположную сторону на гипотенузу, а затем взяв ARCSIN.

Или мы могли бы продемонстрировать еще больше знаний о треугольниках, используя вычитание, чтобы найти его, поскольку мы знаем, что сумма внутренних углов треугольника должна составлять 180°. Вычитание угла, который мы только что нашли, из 180°, а затем вычитание нашего известного прямого угла (90°) также даст нам третий угол.

Этот калькулятор отлично подходит для получения всей этой информации только с двух сторон прямоугольного треугольника, но это забавная задача, чтобы попытаться найти стороны, углы, площадь и периметр самостоятельно без него.